diff --git a/apps/blog/_posts/algorithm/leetcode/hard/42.md b/apps/blog/_posts/algorithm/leetcode/hard/42.md
new file mode 100644
index 00000000..d8e1d4d0
--- /dev/null
+++ b/apps/blog/_posts/algorithm/leetcode/hard/42.md
@@ -0,0 +1,117 @@
+---
+title: '[LeetCode] 42. Trapping Rain Water'
+description: '2차원 좌표의 영역을 빠르게 구해보자'
+tags: ['algorithm', 'leetcode', 'hard', 'stack', 'two-pointers']
+coverImage: 'https://github.com/1ilsang/dev/assets/23524849/e0fcd614-46f9-4221-a284-570b9591a1b8'
+date: '2023-10-14T08:10:32.304Z'
+ogImage:
+ url: 'https://github.com/1ilsang/dev/assets/23524849/e0fcd614-46f9-4221-a284-570b9591a1b8'
+---
+
+ +
+> [문제 링크](https://leetcode.com/problems/trapping-rain-water)
+
+빗물이 고일 수 있는 모든 영역을 구하면 되는 문제다.
+
+기본적으로 물은 '높은 곳에서 낮은 곳'으로 흐르기 때문에 우리는 높이를 비교하면서 빗물이 고일 수 있는지 판단해야 한다.
+
+이 문제는 두 가지 스택과 투포인터 두 가지로 풀 수 있다. 두 방법 모두 알아두면 좋기 때문에 두 가지 해석을 모두 하려고 한다.
+
+## 접근법 1. Stack O(n) T(n)
+
+스택 접근은 "가로로 면적을 합해가는" 방식이다.
+
+빗물이 고이기 위해서는 양쪽으로 벽이 있어야 한다.
+
+스택을 활용해 양 벽을 계산하는 방법은, 높이가 감소할 때는 스택에 푸쉬하고 높이가 이전 탑보다 높아질 때는 팝을 하면서 얼마만큼의 빗물을 저장할 수 있는지 계산하면 된다.
+
+
+
+0번째 높이부터 순회해 보자.
+
+1. 모든 원소를 순회할 때마다 스택에 푸쉬한다. 왼쪽의 그림과 같이 높이가 감소해 나갈 때에는 특별한 작업 없이 계속 진행한다.
+2. 중앙의 그림(`i = 3`)의 상황일 경우 현재 벽이 스택의 Top 값보다 더 높기 때문에 빗물이 고일 수 있다. 현재 높이와 같거나 클 때까지 스택에 쌓여있는 벽들을 pop 하며 "가로로" 누적값을 더한다. 여기서는 높이 1이 최대이므로 스택에 추가된 높이 2(`i = 0`)까지 계산하지 않고 끝난다.
+3. 우측의 그림(`i = 4`)에서도 동일하다. 현재 높이보다 큰 높이가 나올 때까지 팝을 하며 계산한다. 2번에서 이미 높이 1일 때의 경우를 계산했으므로 높이 2일 때의 가로 값만 계산하면 된다.
+
+마지막 노드까지 위의 방식을 계속해서 하면 모든 면적을 구할 수 있다. 코드와 라인별 해석은 제일 아래에 작성해 두었다.
+
+## 접근법 2. Two Pointers O(n) T(1)
+
+투포인터 접근은 "세로로 면적을 합해가는" 방식이다.
+
+빗물이 고이기 위해서는 양쪽으로 벽이 있어야 한다.
+
+투포인터는 양끝에 포인터를 설정하고 좌우로 움직이며 높이가 더 높은 쪽을 향해 간다. 높이가 높은 쪽을 향해 양 포인터를 옮기면 반대로 낮은 쪽은 빗물이 고이는 곳이기 때문에 세로로 더해나가면 된다.
+
+
+
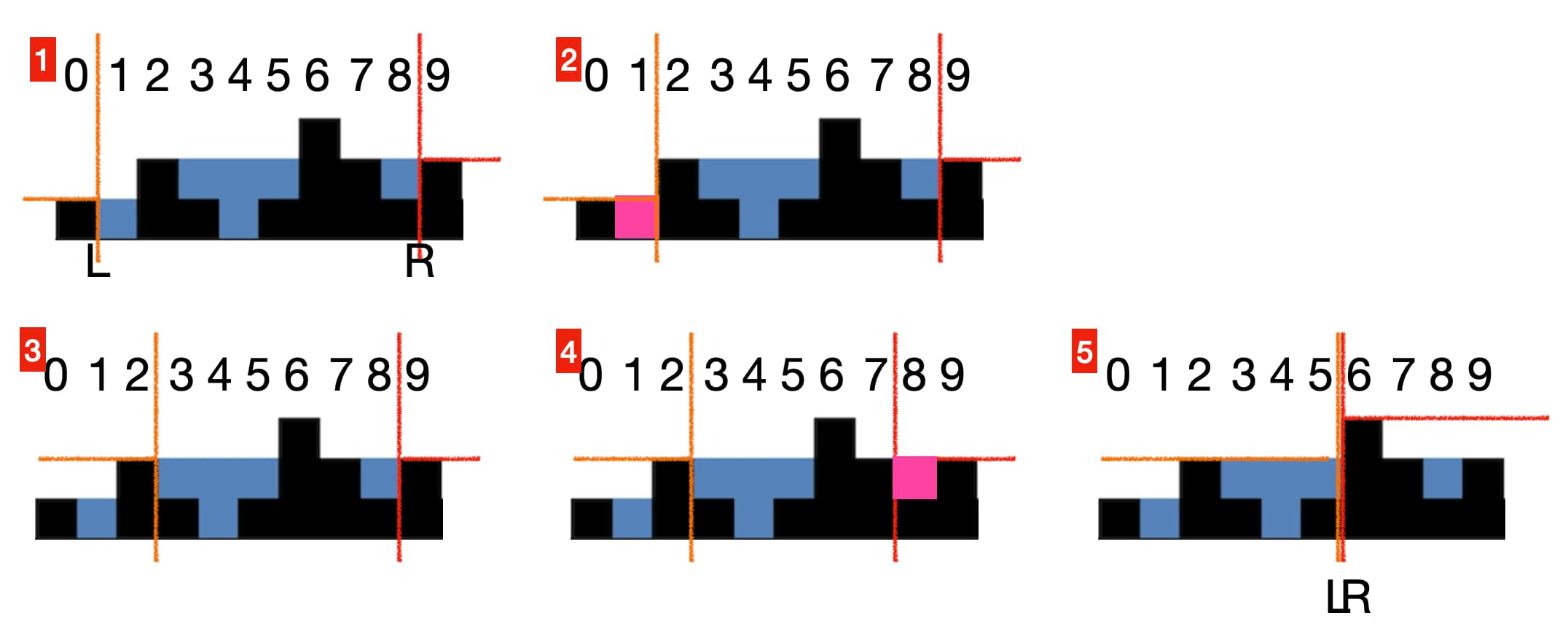
+L, R을 양 끝에 두고 순회하면서 각각 MAX 값을 구한다.
+
+1. 최초의 상태. 최대값(가로선)을 설정한다.
+2. `L < R`이라면 L을 옮기고 아니면 R을 옮긴다. 여기는 L를 옮겼다. `i = 1`의 높이가 L의 최대높이보다 낮으므로 그 차이를 더한다.
+3. `L < R`일 때까지 L을 옮긴 모습이다.
+4. R을 옮겼다. `i = 8`의 높이가 R의 최대높이보다 낮으므로 그 차이를 더한다.
+5. 계속해서 반복하면 결국 LR은 한곳으로 모이고 그 사이의 모든 세로 값이 더해져 빗물의 면적을 구할 수 있다.
+
+## 최종 코드
+
+```js
+// Stack
+const trap = (height) => {
+ let res = 0;
+ let i = 0;
+ const stack = [];
+
+ while (i < height.length) {
+ const curHeight = height[i];
+ // 현재 높이가 스택의 마지막 높이보다 높다면
+ while (stack.length > 0 && height[stack[stack.length - 1]] < curHeight) {
+ const lastI = stack.pop();
+ // 스택이 비었다는 의미는 자신뿐이므로 빗물이 고일 수 없기 때문에 탈출한다.
+ if (stack.length === 0) break;
+ const peekI = stack[stack.length - 1];
+ // 현재 위치(i)와 스택의 다음 위치(peekI)의 거리를 구한다.
+ const dist = i - peekI - 1;
+ // 현재 위치의 높이와 스택의 다음 위치 높이중 낮은 값을 기준으로 스택의 마지막 높이를 뺀다.
+ // 마지막 높이만큼은 빗물이 고일 수 없기 때문
+ const h = Math.min(curHeight, height[peekI]) - height[lastI];
+ res += dist * h;
+ }
+ stack.push(i++);
+ }
+
+ return res;
+};
+```
+
+```js
+// Two-pointers
+const trap = (height) => {
+ let res = 0;
+ let l = 0;
+ let r = height.length - 1;
+ let lMax = 0;
+ let rMax = 0;
+
+ while (l < r) {
+ const curLeft = height[l];
+ const curRight = height[r];
+ // 매번 max 값을 갱신한다. 그래야 자신이 줄어든 값인지 비교할 수 있다.
+ lMax = Math.max(curLeft, lMax);
+ rMax = Math.max(curRight, rMax);
+
+ // 현재 높이가 최대값 보다 적다면 고일 수 있으므로 추가한다.
+ if (curLeft < lMax) {
+ res += lMax - curLeft;
+ }
+ if (curRight < rMax) {
+ res += rMax - curRight;
+ }
+ // 양쪽의 포인터를 비교해서 높이가 더 큰 방향으로 이동한다.
+ curLeft < curRight ? l++ : r--;
+ }
+
+ return res;
+};
+```
+
+> [문제 링크](https://leetcode.com/problems/trapping-rain-water)
+
+빗물이 고일 수 있는 모든 영역을 구하면 되는 문제다.
+
+기본적으로 물은 '높은 곳에서 낮은 곳'으로 흐르기 때문에 우리는 높이를 비교하면서 빗물이 고일 수 있는지 판단해야 한다.
+
+이 문제는 두 가지 스택과 투포인터 두 가지로 풀 수 있다. 두 방법 모두 알아두면 좋기 때문에 두 가지 해석을 모두 하려고 한다.
+
+## 접근법 1. Stack O(n) T(n)
+
+스택 접근은 "가로로 면적을 합해가는" 방식이다.
+
+빗물이 고이기 위해서는 양쪽으로 벽이 있어야 한다.
+
+스택을 활용해 양 벽을 계산하는 방법은, 높이가 감소할 때는 스택에 푸쉬하고 높이가 이전 탑보다 높아질 때는 팝을 하면서 얼마만큼의 빗물을 저장할 수 있는지 계산하면 된다.
+
+
+
+0번째 높이부터 순회해 보자.
+
+1. 모든 원소를 순회할 때마다 스택에 푸쉬한다. 왼쪽의 그림과 같이 높이가 감소해 나갈 때에는 특별한 작업 없이 계속 진행한다.
+2. 중앙의 그림(`i = 3`)의 상황일 경우 현재 벽이 스택의 Top 값보다 더 높기 때문에 빗물이 고일 수 있다. 현재 높이와 같거나 클 때까지 스택에 쌓여있는 벽들을 pop 하며 "가로로" 누적값을 더한다. 여기서는 높이 1이 최대이므로 스택에 추가된 높이 2(`i = 0`)까지 계산하지 않고 끝난다.
+3. 우측의 그림(`i = 4`)에서도 동일하다. 현재 높이보다 큰 높이가 나올 때까지 팝을 하며 계산한다. 2번에서 이미 높이 1일 때의 경우를 계산했으므로 높이 2일 때의 가로 값만 계산하면 된다.
+
+마지막 노드까지 위의 방식을 계속해서 하면 모든 면적을 구할 수 있다. 코드와 라인별 해석은 제일 아래에 작성해 두었다.
+
+## 접근법 2. Two Pointers O(n) T(1)
+
+투포인터 접근은 "세로로 면적을 합해가는" 방식이다.
+
+빗물이 고이기 위해서는 양쪽으로 벽이 있어야 한다.
+
+투포인터는 양끝에 포인터를 설정하고 좌우로 움직이며 높이가 더 높은 쪽을 향해 간다. 높이가 높은 쪽을 향해 양 포인터를 옮기면 반대로 낮은 쪽은 빗물이 고이는 곳이기 때문에 세로로 더해나가면 된다.
+
+
+
+L, R을 양 끝에 두고 순회하면서 각각 MAX 값을 구한다.
+
+1. 최초의 상태. 최대값(가로선)을 설정한다.
+2. `L < R`이라면 L을 옮기고 아니면 R을 옮긴다. 여기는 L를 옮겼다. `i = 1`의 높이가 L의 최대높이보다 낮으므로 그 차이를 더한다.
+3. `L < R`일 때까지 L을 옮긴 모습이다.
+4. R을 옮겼다. `i = 8`의 높이가 R의 최대높이보다 낮으므로 그 차이를 더한다.
+5. 계속해서 반복하면 결국 LR은 한곳으로 모이고 그 사이의 모든 세로 값이 더해져 빗물의 면적을 구할 수 있다.
+
+## 최종 코드
+
+```js
+// Stack
+const trap = (height) => {
+ let res = 0;
+ let i = 0;
+ const stack = [];
+
+ while (i < height.length) {
+ const curHeight = height[i];
+ // 현재 높이가 스택의 마지막 높이보다 높다면
+ while (stack.length > 0 && height[stack[stack.length - 1]] < curHeight) {
+ const lastI = stack.pop();
+ // 스택이 비었다는 의미는 자신뿐이므로 빗물이 고일 수 없기 때문에 탈출한다.
+ if (stack.length === 0) break;
+ const peekI = stack[stack.length - 1];
+ // 현재 위치(i)와 스택의 다음 위치(peekI)의 거리를 구한다.
+ const dist = i - peekI - 1;
+ // 현재 위치의 높이와 스택의 다음 위치 높이중 낮은 값을 기준으로 스택의 마지막 높이를 뺀다.
+ // 마지막 높이만큼은 빗물이 고일 수 없기 때문
+ const h = Math.min(curHeight, height[peekI]) - height[lastI];
+ res += dist * h;
+ }
+ stack.push(i++);
+ }
+
+ return res;
+};
+```
+
+```js
+// Two-pointers
+const trap = (height) => {
+ let res = 0;
+ let l = 0;
+ let r = height.length - 1;
+ let lMax = 0;
+ let rMax = 0;
+
+ while (l < r) {
+ const curLeft = height[l];
+ const curRight = height[r];
+ // 매번 max 값을 갱신한다. 그래야 자신이 줄어든 값인지 비교할 수 있다.
+ lMax = Math.max(curLeft, lMax);
+ rMax = Math.max(curRight, rMax);
+
+ // 현재 높이가 최대값 보다 적다면 고일 수 있으므로 추가한다.
+ if (curLeft < lMax) {
+ res += lMax - curLeft;
+ }
+ if (curRight < rMax) {
+ res += rMax - curRight;
+ }
+ // 양쪽의 포인터를 비교해서 높이가 더 큰 방향으로 이동한다.
+ curLeft < curRight ? l++ : r--;
+ }
+
+ return res;
+};
+```