前言:本文主要围绕解决TSP旅行商问题展开,对于机器人的路线规划以及非线性方程求解的问题等解决方案大家可以直接参考github源码地址, 对于一些其他智能算法例如遗传算法解决一些现实问题都有实现!! 欢迎小伙伴的star哦~~ 🤭
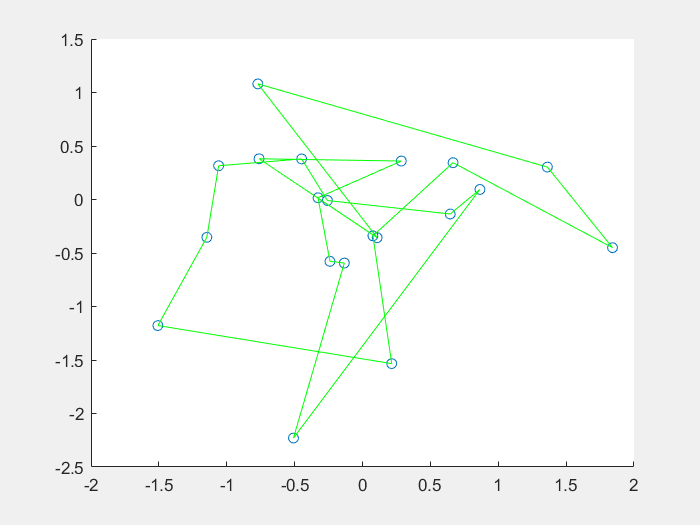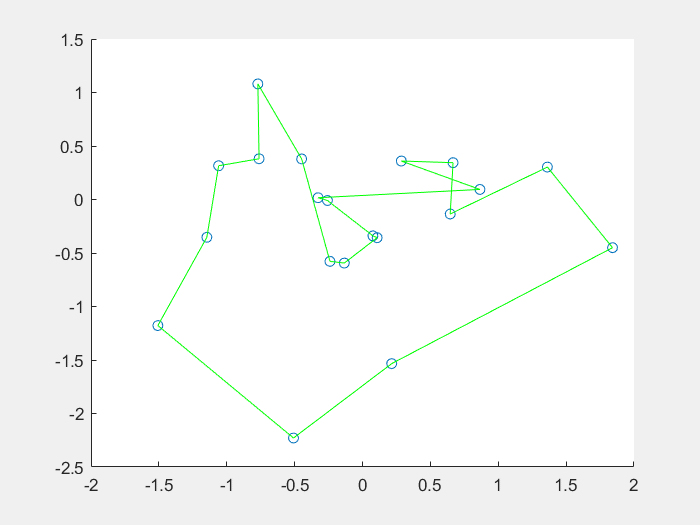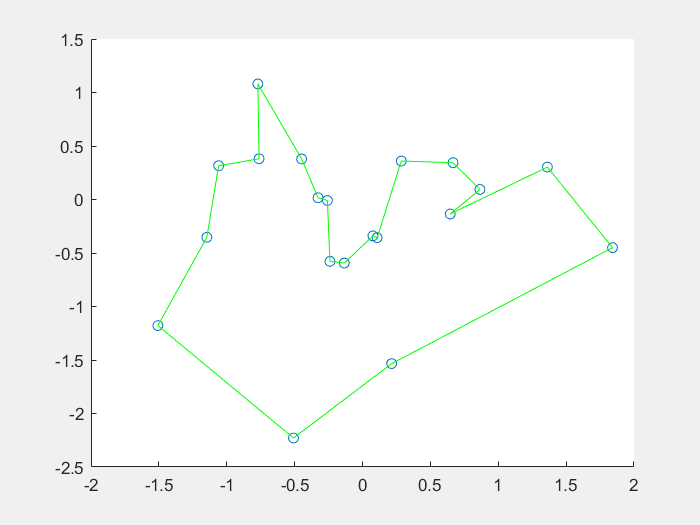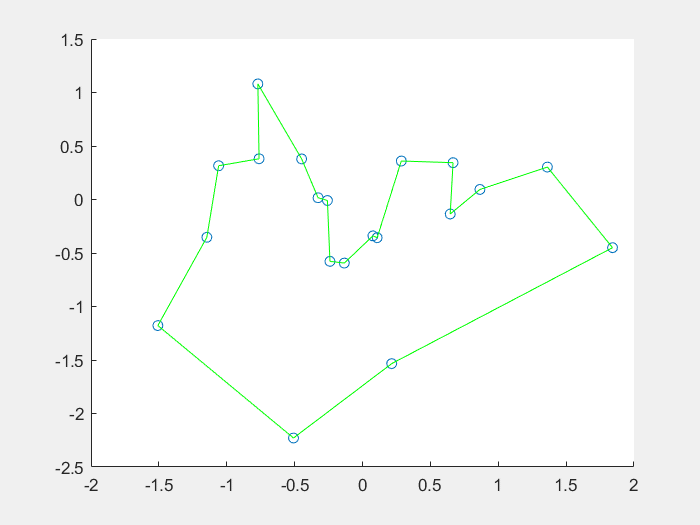
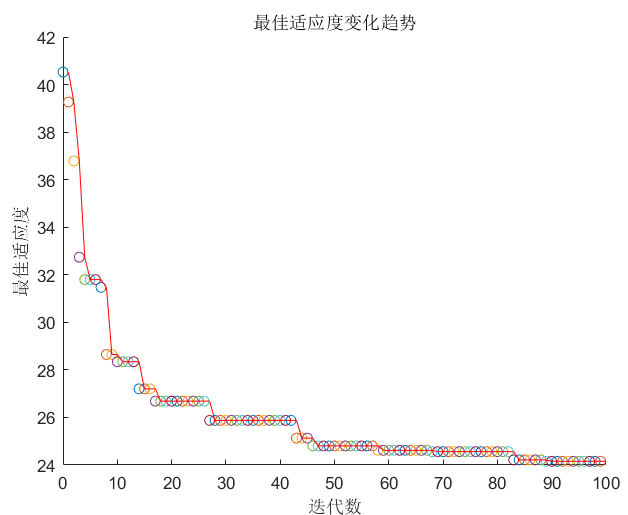
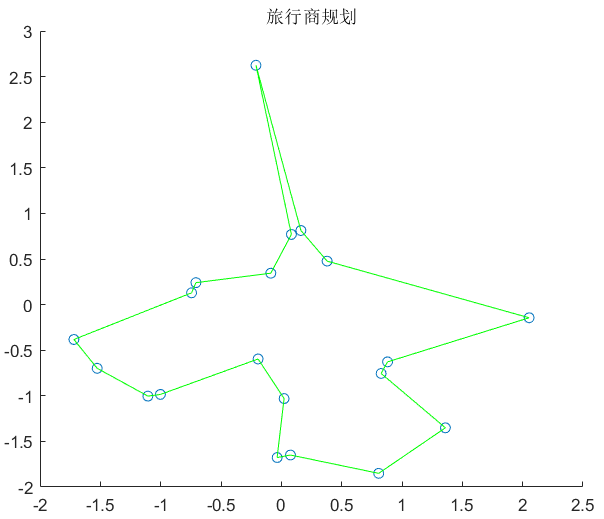
效果图:
将免疫概念及其理论应用于遗传算法,在保留原算法优良特性的前提下,力图有选择、有目的地利用待求问题中的一些特征信息或知识来抑制其优化过程中出现的退化现象,这种算法称为免疫算法(Immune Algorithm) IA。人工免疫算法是一种具有生成+检测 (generate and test)的迭代过程的群智能搜索算法。从理论上分析,迭代过程中,在保留上一代最佳个体的前提下,免疫算法是全局收敛的。
也就是说,免疫算法的思想来自于生物体的免疫机制,构造具有动态性和自适应性的信息防御机制,用来抵抗外部无用的有害信息的侵入(退化解),从而保证信息的有效性和无害性(最优解)。 注:退化解的来自于变异等操作过后的适应度值低于父类的解。
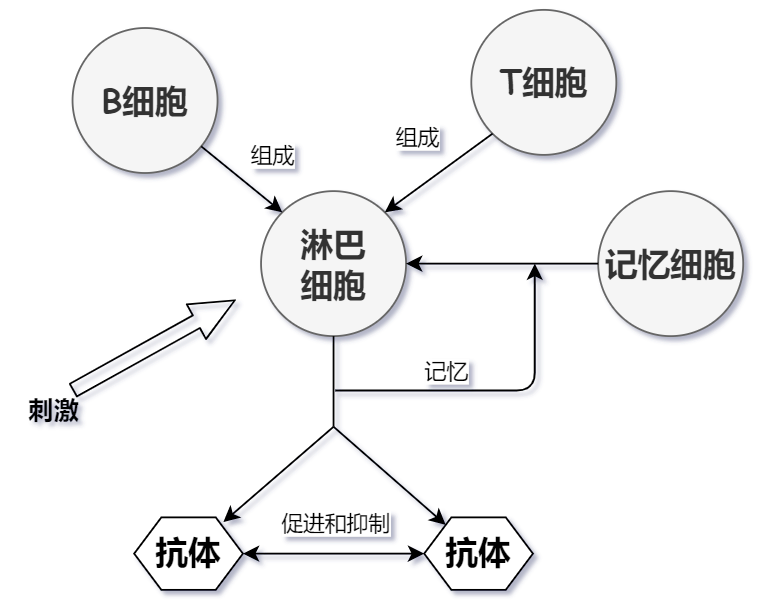
在生物课上学过,免疫系统的构成元素主要是淋巴细胞,淋巴细胞包括B细胞和T细胞。
- T细胞主要在收到抗原刺激后可以分化成淋巴母细胞,产生多种淋巴因子,引起细胞免疫反应。
- B细胞又称为抗体形成细胞,可以产生抗体,抗体会同抗原产生一系列的反应,最后通过吞噬细胞的作用来消灭抗原。并且抗体具有专一性,而且免疫系统具备识别能力和记忆能力,可以对旧抗原做出更快的反应。
免疫系统和一般免疫算法的比较:
| 免疫系统 | 免疫算法 |
|---|---|
| 抗原 | 待解决的问题,例如方程最优解、TSP等等 |
| 抗体 | 最优解 |
| 抗原识别 | 问题识别 |
| 从记忆细胞产生抗体 | 找到以往的成功例子 |
| 淋巴细胞的分化 | 最优解的保持 |
| 细胞抑制 | 剩余候选解的消除 |
| 抗体增强 | 利用遗传算子产生新的抗体 |
免疫遗传算法解决了遗传算法早熟收敛的问题,有可能陷入局部最优解的情况,并且遗传算法具有一定的盲目性,尤其是在交叉和变异的过程中。容易产生相较于父类更加差的解,也就是退化现象的出现。如果在遗传算法中引入免疫的方法和概念,对遗传算法全局搜索进行干预,就避免了很多重复的工作。
免疫算法在面对求解问题的时候,相当于面对各种抗原,可以提前注射疫苗,来一只退化的现象,从而保持优胜略汰的特点,使算法一直优化下去。
一般的免疫算法分为下面 3 种情况。
- 模仿免疫系统抗体与抗原的识别,结合抗体的产生过程而抽象出来的免疫算法。
- 基于免疫系统中的其他特殊机制抽象出来的算法,例如克隆选择算法。
- 和其他智能算法等其他的算法进行融合,例如免疫遗传算法。
免疫遗传算法和遗传算法的结构一致,最大的不同之处在于在免疫遗传算法中引入了浓度调节机制。在进行选择操作的时候,遗传算法制只利用了适应度指标对个体进行评价;在免疫遗传算法当中,免疫遗传算法中的选择策略变为:适应度越高,浓度越小,个体复制的概率越大,反之越小。
免疫遗传算法的基本思想就是在传统的算法基础上加入一个免疫算子,加入免疫算子的目的就是为了防止种群的退化。免疫算子有接种疫苗和免疫选择两个步骤组成。免疫遗传算法可以有效地调节选择压力。因此免疫算法可以保持种群多样性的能力。
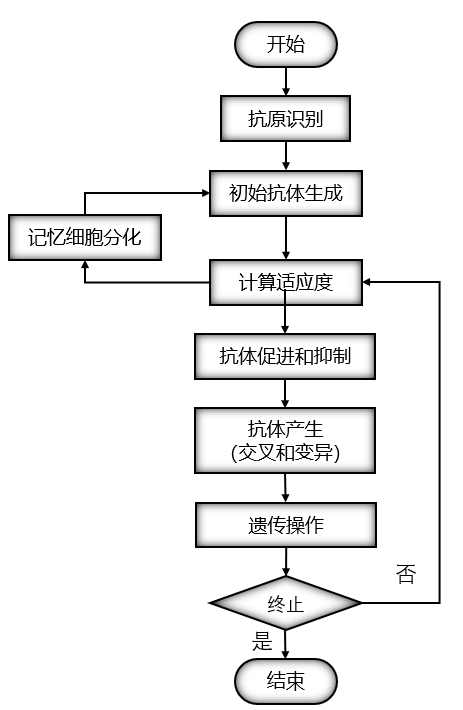
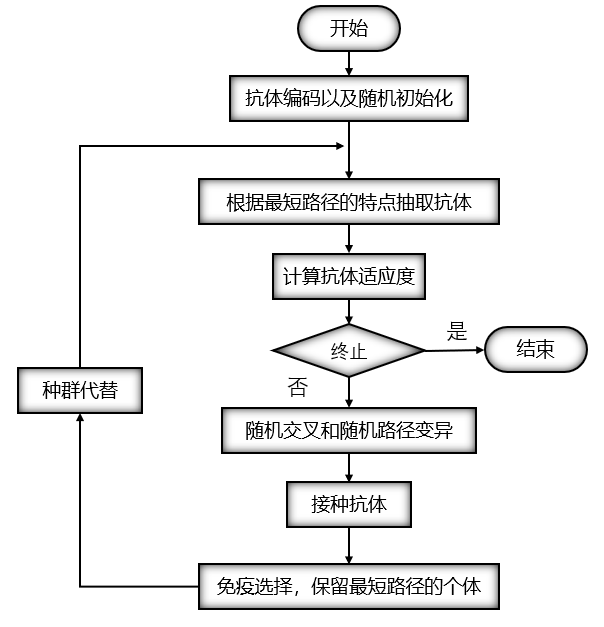
免疫遗传算法的步骤和流程:
TSP问题是所有智能算法都要解决的问题,TSP问题就是旅行商问题,旅行商要遍历所有的城市,并且城市仅能通过一次,并且保证所经过的城市的路径最小。
对于个体的编码仍然采用和遗传算法中相同的实数编码结构。由于本例中要求路径最低,适应度函数就取为路径的倒数。
采用单点交叉,交叉的位置随机,类似与遗传算法。每次遗传操作后,随机抽取一些个体进行注射抗体,进行免疫检测,即对接种了个体进行检测,如果适应度提高,则继续,否则就代表着在进行交叉和变异的过程中出现了退化现象,这时个体就会被父类代替,就是下面的表达式:
父类适应度 < 子类适应度 ? 子类 : 父类主要是对参数进行初始化,包括对一些概率参数、初始种群矩阵,城市初始位置、城市之间的距离矩阵等等。 参数初始化:
N = 20;
%城市的个数
M = N - 1;
%种群的个数
pos = 50 * randn(N,2);
%%生成城市的坐标
global D;
%城市距离数据
D = zeros(N,N);
for i = 1 : N
for j = i + 1 : N
dis = (pos(i, 1)-pos(j, 1)).^2+(pos(i, 2)-pos(j, 2)).^2;
D(i, j) = dis^(0.5);
D(j, i) = D(i, j);
end
end
%中间结果保存
global TmpResult;
TmpResult = [];
global TmpResult1;
TmpResult1 = [];
[M, N] = size(D); % 种群规模
pCharChange = 1; % 个体换位概率
pStrChange = 0.4; % 个体移位概率
pStrReverse = 0.4; % 个体逆转概率
pCharReCompose = 0.4; % 个体重组概率
MaxIterateNum = 100; % 迭代次数
mPopulation = zeros(N-1,N);
mRandM = randperm(N-1); % 最优路径
mRandM = mRandM + 1;
for rol = 1:N-1
mPopulation(rol,:) = randperm(N);%产生初始抗体
end迭代过程:
count = 0;
figure(2);
while count < MaxIterateNum
% 产生新抗体
B = Mutation(mPopulation, [pCharChange pStrChange pStrReverse pCharReCompose]);
% 计算新产生的抗体对应的适应度,并选择最优抗体
mPopulation = SelectAntigen(mPopulation,B);
% 保存每一代最优的个体
best_pop(count + 1, :) = mPopulation(1, :);
count = count + 1;
end变异过程,变异的过程主要保存移位、换位、逆转以及重组操作,这几个操作之间相互独立,最后拼接在一起后返回。 变异操作:
function result = Mutation(A, P)
[m,n] = size(A);
% 换位
n1 = round(P(1)*m); % 变异的个体数
m1 = randperm(m); % 混淆个体顺序
cm1 = randperm(n-1)+1; % 个体变异的位置
B1 = zeros(n1,n); % 保存变异后的个体
c1 = cm1(n-1);
c2 = cm1(n-2);
for s = 1:n1
B1(s,:) = A(m1(s),:);
tmp = B1(s,c1);
B1(s,c1) = B1(s,c2);
B1(s,c2) = tmp;
end
% 移位
n2 = round(P(2)*m);
m2 = randperm(m);
cm2 = randperm(n-1)+1;
B2 = zeros(n2,n);
c1 = min([cm2(n-1),cm2(n-2)]);
c2 = max([cm2(n-1),cm2(n-2)]);
for s = 1:n2
B2(s,:) = A(m2(s),:);
B2(s,c1:c2) = DisplaceStr(B2(s,:),c1,c2);
end
% 逆转
n3 = round(P(3)*m);
m3 = randperm(m);
cm3 = randperm(n-1)+1;
B3 = zeros(n3,n);
c1 = min([cm3(n-1),cm3(n-2)]);
c2 = max([cm3(n-1),cm3(n-2)]);
for s = 1:n3
B3(s,:) = A(m3(s),:);
tmp1 = [[c2:-1:c1]',B3(s,c1:c2)'];
tmp1 = sortrows(tmp1,1);
B3(s,c1:c2) = tmp1(:,2)';
end
% 重组
n4 = round(P(4)*m);
m4 = randperm(m);
cm4 = randperm(n-1)+1;
B4 = zeros(n4,n);
c1 = min([cm4(n-1),cm4(n-2)]);
c2 = max([cm4(n-1),cm4(n-2)]);
for s = 1:n4
B4(s,:) = A(m4(s),:);
B4(s,c1:c2) = CharRecompose(B4(s,c1:c2));
end
% 变异后个体拼接
result = [B1;B2;B3;B4];上面的涉及几个函数分别是DisplaceStr()以及CharRecompose()
function result = DisplaceStr(inMatrix, startCol, endCol)
[m,n] = size(inMatrix);
if n <= 1
result = inMatrix;
return;
end
switch nargin
case 1
startCol = 1;
endCol = n;
case 2
endCol = n;
end
mMatrix1 = inMatrix(:,(startCol + 1):endCol);
result = [mMatrix1, inMatrix(:, startCol)];
function result = CharRecompose(A)
global D;
index = A(1,2:end);
tmp = A(1,1);
result = [tmp];
[m,n] = size(index);
while n>=2
len = D(tmp,index(1));
tmpID = 1;
for s = 2:n
if len > D(tmp,index(s))
tmpID = s;
len = D(tmp,index(s));
end
end
tmp = index(tmpID);
result = [result,tmp];
index(:,tmpID) = [];
[m,n] = size(index);
end
result = [result,index(1)];选择优秀的个体继续进行后续的操作,对于退化或者次优解进行去除。 选择抗体:
function result = SelectAntigen(A,B)
global D;
[m,n] = size(A);
[p,q] = size(B);
index = [A;B];
rr = zeros((m+p),2);
rr(:,2) = [1:(m+p)]';
for s = 1:(m+p)
for t = 1:(n-1)
rr(s,1) = rr(s,1)+D(index(s,t),index(s,t+1));
end
rr(s,1) = rr(s,1) + D(index(s,n),index(s,1));
end
rr = sortrows(rr,1);
ss = [];
tmplen = 0;
for s = 1:(m+p)
if tmplen ~= rr(s,1)
tmplen = rr(s,1);
ss = [ss;index(rr(s,2),:)];
end
end
global TmpResult;
TmpResult = [TmpResult;rr(1,1)];
global TmpResult1;
TmpResult1 = [TmpResult1;rr(end,1)];
result = ss(1:m,:);注: 为了说明方便将代码直接拆开展示如果需要源码可以直接最后的源码地址中找到。
更多精彩内容,大家可以转到我的主页:曲怪曲怪的主页
源码地址:github地址