给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-inorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
注意给定root直接可以去遍历访问左右节点 递归解法: 左右子树递归使用自身方法
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
res = []
if root.left :
res += self.inorderTraversal(root.left)
res.append(root.val)
if root.right:
res += self.inorderTraversal(root.right)
return res
非递归的方式: 基本想法: 用栈来保存节点 一路向左下(直到最深处) 为空时 弹出一个节点(已经在左子树的最深处,弹出的是上一层的节点),先输出,再转向右子树
先考虑左子树一直往下 左子树为空时,返回这个子树的根节点(stack的顶部节点) 再转向右节点
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res, stack= [], []
cur = root
while cur or stack:
while cur:
stack.append(cur)
cur = cur.left
#先考虑的是左子树 当前左子树为空 stack才返回根节点 并输出
cur = stack.pop()
res.append(cur.val)
cur = cur.right
return res
或者:
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res, stack= [], []
cur = root
while cur or stack:
if cur:
stack.append(cur)
cur = cur.left
else:
cur = stack.pop()
res.append(cur.val)
cur = cur.right
return res
递归解法:
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
res = []
res.append(root.val)
res += self.preorderTraversal(root.left)
res += self.preorderTraversal(root.right)
return res
非递归解法 基于栈的实现 用栈来装节点的左右子树,注意先放右子树,再放左子树 出栈时顺序相反符合条件
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
stack, res = [root,], []
while stack:
item = stack.pop()
if item:
res.append(item.val)
if item.right:
stack.append(item.right)
if item.left:
stack.append(item.left)
return res
和中序遍历很相似的非递归方法 区别也就是 结果添加元素的位置不同 (大致类似)
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
stack, res, node= [], [], root
while node or stack:
while node:
stack.append(node)
res.append(node.val)
node = node.left
node = stack.pop()
node = node.right
return res
递归解法:
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
res = []
res += self.postorderTraversal(root.left)
res += self.postorderTraversal(root.right)
res.append(root.val)
return res
考虑和先序遍历的关联性 先序遍历的顺序是: 根-左-右 后序遍历的顺序是 :左-右-根 考虑的是 将先序遍历的左右逆反,根右左 然后对结果进行 逆序即可
所以直接关联先序遍历的代码 交换左右顺序 然后结果逆序(上面两种先序遍历的非递归方式都可以变化)
非逆序先序遍历的方法 很重要:(待补充) 比起前序与中序遍历,后续非递归遍历多了一个辅助变量pre来判断右节点是否被访问过
https://www.jianshu.com/p/456af5480cee 很好的总结 尤其是关于后序遍历 图片很清晰明了 后续遍历和先序、中序遍历不太一样。
后序遍历在决定是否可以输出当前节点的值的时候,需要考虑其左右子树是否都已经遍历完成。
所以需要设置一个lastVisit游标。
若lastVisit等于当前考查节点的右子树,表示该节点的左右子树都已经遍历完成,则可以输出当前节点。
并把lastVisit节点设置成当前节点,将当前游标节点node设置为空,(或者不要用同样的node 用一个top来表示)下一轮就可以访问栈顶元素。
否者,需要接着考虑右子树,node = node.right。
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
stack, res, node = [], [], root
pre = None
while node or stack:
while node:
stack.append(node)
node = node.left
#获取栈顶节点,先不出栈
node = stack[-1]
#若右节点已经访问过或者没有右节点 则输出该节点值 如果栈顶节点没有右孩子,或者已经遍历过了它的右孩子,就输出该节点
if not node.right or node.right == pre :
res.append(node.val)
#更新pre节点 并出栈
pre = node
stack.pop()
#因为把栈顶的节点和要遍历的搞混了
node = None
#否则,准备将栈顶节点的右孩子入栈
else:
node = node.right
return res
或者 不要用同样的node 用一个top来表示
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
stack, res, node = [], [], root
pre = None
while node or stack:
while node:
stack.append(node)
node = node.left
#使用新的变量 top 而不是只用node
top = stack[-1]
if not top.right or top.right == pre :
res.append(top.val)
pre = top
stack.pop()
else:
node = top.right
return res
实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。
调用 next() 将返回二叉搜索树中的下一个最小的数。
next() 和 hasNext() 操作的时间复杂度是 O(1),并使用 O(h) 内存,其中 h 是树的高度。
主要是对非递归版本的遍历不清晰,使用栈可以使得空间复杂度为O(h) 因为到达最深处之后就会往回撤 符合空间复杂度
class BSTIterator:
#难点在于如何 使用O(h)的内存 其实还是中序遍历 ,只不过用非递归方式即 栈的方式,则最多可入栈O(h)个数。然后要出栈,因此时间复杂度符合要求
def __init__(self, root: TreeNode):
self.stack = []
while root:
self.stack.append(root)
root = root.left
def next(self) -> int:
res = self.stack.pop()
tmp = res.right
while tmp:
self.stack.append(tmp)
tmp = tmp.left
return res.val
def hasNext(self) -> bool:
if self.stack:
return True
return False
给定一个整数 n,求以 1 ... n 为节点组成的二叉搜索树有多少种?
示例:
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-binary-search-trees
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
动态规划的思想 主要是思路 代码很简单:
G(n) 表示n个点 一共的二叉搜索数的个数 即本题中的目标
G(n) 可以表示为 分别以 1,2, ...n 为根节点的二叉搜索树 这就是不同的 大问题-》单独的小问题 G(n) = f(1,n) + f(2,n) + ... f(n,n)
f(i,n) 的二叉树即 以i节点为根节点 前面i-1个数小于i 后面 n-i个数大于i 即左右子树的不同个数 则f(i,n) = G(i-1) * G(n-i) (注意到 G(i)只和数的个数有关系)
因此 G(n) 可以表示为 G(n) = G(0)*G(n-1) + G(1)*G(n-2) + G(2)* G(n-3) + ... G(n-1)*G(0)
另外一种表述: 做题的思路,想象一下f(4)有几种情况,其实就4种,分别是以1为根,以2为根,以3为根,和以4为根。 我们分别讨论4种根情况个数: 如果以1为根,那么剩余的数只能在1的右子树,且剩余数也是按顺序234,相当于f(3)的个数。故1为根有f(0) * f(3) = 5; 同理,以2为根,左子树只可能1,右子树是34,共有f(1)*f(2)=2; 以3为根,f(2)*f(1)=2,以4为根,f(3) * f(0) = 5
class Solution:
def numTrees(self, n: int) -> int:
G = [0] * (n+1)
G[0], G[1] = 1, 1
for i in range(2, n+1):
for j in range(1, i+1):
G[i] += G[j-1]*G[i-j]
return G[n]
给定一个整数 n,生成所有由 1 ... n 为节点所组成的二叉搜索树。
示例:
输入: 3
输出:
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-binary-search-trees-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
在上题的思想上 递归调用自身 (在考虑回溯得时候自己总是纠结 for循环左右子树如何进入 for循环的每一个数 然后判断该进入左右子树即可 而不是全部遍历 )
class Solution:
def generateTrees(self, n: int) -> List[TreeNode]:
if n == 0:
return []
return self.recursion(1, n)
def recursion(self, start, end):
res = []
if start > end:
return [None]
for i in range(start, end+1):
lefts = self.recursion(start, i-1)
rights = self.recursion(i+1, end)
for oneleft in lefts:
for oneright in rights:
node = TreeNode(i)
node.left = oneleft
node.right = oneright
res.append(node)
return res
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/validate-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
- 用中序遍历的方式 判断中序遍历之后是否事升序
- 用递归的方式
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
if not root:
return True
last, stack= None, []
cur = root
while cur or stack:
while cur:
stack.append(cur)
cur = cur.left
cur = stack.pop()
if last and cur.val<=last.val:
return False
#res.append(cur.val)
last = cur
cur = cur.right
return True
递归 可以学习这个边界的写法 (float("-inf") float("inf")) 利用了最大最小值的边界 这种递归比自己一开始的清晰多了 也是原来的三个步骤 什么时候终止 返回什么 每一层做什么
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
def isBST(root, minval, maxval):
if not root:
return True
if root.val <= minval or root.val >= maxval:
return False
return isBST(root.left, minval, root.val) and isBST(root.right, root.val, maxval)
return isBST(root, float("-inf"), float("inf"))
二叉搜索树中的两个节点被错误地交换。
请在不改变其结构的情况下,恢复这棵树。
示例 1:
输入: [1,3,null,null,2]
1
/
3
\
2
输出: [3,1,null,null,2]
3
/
1
\
2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/recover-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
还是在中序遍历二叉搜索树(递归和迭代的方式),然后找到两个逆序的节点,进行交换 重点是两个节点的寻找 第一个节点简单 就是第一个逆序的 last 第二个节点是 最后面的一个逆序元素 cur 见代码
class Solution:
def recoverTree(self, root: TreeNode) -> None:
"""
Do not return anything, modify root in-place instead.
"""
firstnode = None
secondnode = None
last = TreeNode(float("-inf"))
cur, stack = root, []
while cur or stack:
while cur:
stack.append(cur)
cur = cur.left
cur = stack.pop()
if not firstnode and last.val >= cur.val :
firstnode = last
if firstnode and last.val >= cur.val:
secondnode = cur
#print(secondnode)
last = cur
cur = cur.right
firstnode.val, secondnode.val = secondnode.val, firstnode.val
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/symmetric-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
自己一开始的递归解法: 和官方解法 思路是一致的 但是时间复杂度比较差
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
# 层次遍历之后 直接比较数组元素 最后2^(n-1) 个元素是否前后对称
def judge(p, q):
if p.val == q.val:
if p.left and q.right:
flag1 = judge(p.left, q.right)
elif not p.left and not q.right:
flag1 = True
else:
flag1 = False
if p.right and q.left:
flag2 = judge(p.right, q.left)
elif not p.right and not q.left:
flag2 = True
else:
flag2 = False
return flag1 and flag2
else:
return False
if not root :
return True
if root.left and root.right:
return judge(root.left, root.right)
elif not root.left and not root.right:
return True
else:
return False
改进之后的 思路相差不大 比较巧妙的是 和自己做比较 省去了很多的前界判断 还有就是在传过来再判断是否为空 (同时这也是100题的思路 大致类似)
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
def judge(p, q):
if not p and not q:
return True
if not p or not q:
return False
if p.val == q.val:
return judge(p.left, q.right) and judge(p.right, q.left)
return False
return judge(root, root)
还可以通过层次遍历二叉树(102题),然后比较每一层的元素 是否是回文数组 来判断 注意此时 有null情况要保存下来 用none 本题中层次遍历也是用两个list来完成队列
def isSymmetric(self, root):
queue = [root]
while(queue):
next_queue = list()
layer = list()
for node in queue:
if not node:
layer.append(None)
continue
next_queue.append(node.left)
next_queue.append(node.right)
layer.append(node.val)
if layer != layer[::-1]:
return False
queue = next_queue
return True
给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-level-order-traversal
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
用deque的两种方法来做 append() 以及popleft() 就是一个队列 本题中还要注意的就是 有层次的要求 不用层不同保存
from collections import deque
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
levels = []
if not root:
return levels
#初始化队列 和层次
level = 0
queue = deque([root])
while queue:
#每一层的个数就是每层一开始的队列长度
levels.append([])
level_length = len(queue)
for i in range(level_length):
tmp = queue.popleft()
levels[level].append(tmp.val)
if tmp.left:
queue.append(tmp.left)
if tmp.right:
queue.append(tmp.right)
#到下一层
level += 1
return levels
也可以使用两个list 分别来保存这层和一下层的元素来做 思路是相似的
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
cur = [root]
res = []
while cur:
tmp = []
next = []
cur_len = len(cur)
for i in range(cur_len):
tmp.append(cur[i].val)
if cur[i].left:
next.append(cur[i].left)
if cur[i].right:
next.append(cur[i].right)
res.append(tmp)
cur = next
return res
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---
同样是二叉树层次遍历,注意和上面一题比较 用的stack insert逆序插入 出栈 102 直接使用下表来访问对应的元素
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
#层次遍历的最后一个元素
if not root :
return []
node = root
stack, res = [node], []
next = []
while stack:
cur = stack.pop()
if cur.left:
next.insert(0, cur.left)
if cur.right:
next.insert(0, cur.right)
if not stack:
res.append(cur.val)
stack = next
next = []
#print(res)
return res
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这道题和下一道是同一类型 主要思想都是 递归+ 区分出根节点和左右子树
- 利用前序遍历(root为第一个元素)和后续遍历(root在最后一个元素) 找到root
- 利用中序遍历和 上面得知的root 将数组分为左子树和右子树
- 递归调用自身 输入左右子树的 前序(后序)以及中序的list
- 总结: 可以利用前序(后序)+中序来构造出二叉树
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
#依据两个遍历顺序得出 树的结构
if not preorder:
return None
if len(preorder) == 1:
return TreeNode(preorder[0])
root = TreeNode(preorder[0])
i = inorder.index(preorder[0])
root.left = self.buildTree(preorder[1:i+1], inorder[:i])
root.right = self.buildTree(preorder[i+1:], inorder[i+1:])
return root
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
if not postorder:
return None
if len(postorder) == 1:
return TreeNode(postorder[0])
root = TreeNode(postorder[-1])
i = inorder.index(postorder[-1])
root.left = self.buildTree(inorder[:i], postorder[:i])
root.right = self.buildTree(inorder[i+1:], postorder[i:-1])
return root
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
示例:
示例:
给定有序数组: [-10,-3,0,5,9],
一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树:
0
/ \
-3 9
/ /
-10 5
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
主要思路: 给定列表中的中间元素将会作为二叉搜索树的根,该点左侧的所有元素递归的去构造左子树,同理右侧的元素构造右子树。这必然能够保证最后构造出的二叉搜索树是平衡的。(不太理解原理)
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
#二分法 平衡-》二分法? 递归左右子树即可
if not nums:
return None
left, right = 0, len(nums)-1
mid = (left+right)>>1
#print(mid, nums[mid])
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(nums[:mid])
root.right = self.sortedArrayToBST(nums[mid+1:])
return root
与上题的区别就是 数组变成了链表 主要关键在于如何二分链表
本题最关键的点是 快慢指针法来找到链表的中点
用两个指针,一块一慢,快的每次走两步,慢的每次走一步,这样当快指针遍历结束时,慢指针指向的也就是链表的中间位置。这时候把中间位置的结点的值作为二叉搜索树当前结点的值
class Solution:
def sortedListToBST(self, head: ListNode) -> TreeNode:
#还是仿照上一道题的二分法 递归 分为两个部分 那么问题就是如何二分链表
if not head:
return None
dummy = ListNode(0)
dummy.next = head
count = 0
pre = dummy
fast, slow = head, head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
pre = pre.next
pre.next = None
root = TreeNode(slow.val)
root.left = self.sortedListToBST(dummy.next)
root.right = self.sortedListToBST(slow.next)
return root
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最小深度 2.
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-depth-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
二叉树的很多思路肯定有递归的存在
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
#return min(self.minDepth(root.left), self.minDepth(root.right)) +1
l = self.minDepth(root.left)
r = self.minDepth(root.right)
if l and r:
return min(l, r) + 1
elif l or r:
if l:
return 1+ l
else:
return 1 + r
else:
return 1
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
包括两种方法:递归以及回溯 在112 问题一中递归简单理解 问题二中回溯更加清晰
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
# 二叉树的递归 以及回溯 两种思路
res = []
if not root :
return []
def recursion(root, tmp_res, tmp_sum):
#print(root, tmp_res, tmp_sum)
if not root:
return
if not root.left and not root.right and root.val == tmp_sum :
tmp_res.append(root.val)
res.append(tmp_res[:])
return
recursion(root.left, tmp_res+[root.val], tmp_sum-root.val)
recursion(root.right, tmp_res+[root.val], tmp_sum-root.val)
recursion(root, [], sum)
return res
递归的方法: 注意在子树的结果中要在list的前边插入节点 使用了insert方法
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
# 二叉树的递归 以及回溯 两种思路
if not root:
return []
res = []
if not root.left and not root.right and root.val == sum:
return [[root.val]]
lefts = self.pathSum(root.left, sum-root.val)
if lefts:
for left in lefts:
left.insert(0, root.val)
rights = self.pathSum(root.right, sum-root.val)
if rights:
for right in rights:
right.insert(0, root.val)
return lefts + rights
112中只要求返回true or false 用递归简洁
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
# 二叉树的递归 以及回溯 两种思路
if not root:
return False
if not root.left and not root.right and root.val == sum:
return True
if self.hasPathSum(root.left, sum-root.val) or self.hasPathSum(root.right, sum - root.val):
return True
return False
主要思路就是这样:
# 将左子树插入到右子树的地方
# 将原来的右子树接到左子树的最右边节点
# 考虑新的右子树的根节点,一直重复上边的过程,直到新的右子树为 null
采用递归的方式可读性更佳
def flatten(self, root: TreeNode) -> None:
"""
Do not return anything, modify root in-place instead.
"""
# 将左子树插入到右子树的地方
# 将原来的右子树接到左子树的最右边节点
# 考虑新的右子树的根节点,一直重复上边的过程,直到新的右子树为 null
if not root:
return None
self.flatten(root.left)
self.flatten(root.right)
if root.left:
# 找到最右边元素
most_right = root.left
while most_right.right:
most_right = most_right.right
most_right.right = root.right
root.right = root.left
root.left = None
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
采用递归的方法 每一层的主要操作是 连接自己的左右子树 以及 兄弟节点之间的连接
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return
if root.left:
root.left.next = root.right
if root.next and root.right:
root.right.next = root.next.left
self.connect(root.left)
self.connect(root.right)
return root
非递归的方法:层次遍历 遍历过程中 串联起来(同时解决117)
from collections import deque
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root :
return
queue = deque([root])
while queue:
n = len(queue)
pre_node = None
for _ in range(n):
node = queue.popleft()
if pre_node:
pre_node.next = node
pre_node = node
if node.left:
queue.append(node.left)
queue.append(node.right)
return root
另外的一种方法(同时解决117): 主要思想 下一层有 dummy指针指向头节点之前, 然后tail指针来遍历(相当于每一层的pre指针) 跟随cur指针来遍历一层 -----
- 有一种感觉 在本层把下一层的next链接好 在下一层来cur = cur.next 来遍历这一层
Node connect(Node root) {
Node cur = root;
while (cur != null) {
Node dummy = new Node();
Node tail = dummy;
//遍历 cur 的当前层
while (cur != null) {
if (cur.left != null) {
tail.next = cur.left;
tail = tail.next;
}
if (cur.right != null) {
tail.next = cur.right;
tail = tail.next;
}
cur = cur.next;
}
//更新 cur 到下一层
cur = dummy.next;
}
return root;
}
作者:windliang
链接:https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-28/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
一开始容易理解的解法:
class Solution:
res = float('-inf')
def maxPathSum(self, root: TreeNode) -> int:
self.maxValue(root)
return self.res
# 递归时记录好全局最大和,返回联络最大和。
# 注意是没有分支的 不会出现某个节点 是子节点 但是同时拥有 左右子树 倒Y不符合要求
# 最大路径和:根据当前节点的角色,路径和可分为两种情况:
# 一:以当前节点为根节点
# 1.只有当前节点
# 2.当前节点+左子树
# 3.当前节点+右子书
# 4.当前节点+左右子树
# 这四种情况的最大值即为以当前节点为根的最大路径和
# 此最大值要和已经保存的最大值比较,得到整个树的最大路径值
# 二:当前节点作为父节点的一个子节点
# 和父节点连接的话则需取【单端的最大值】
# 1.只有当前节点
# 2.当前节点+左子树
# 3.当前节点+右子书
# 这三种情况的最大值
def maxValue(self, root):
if not root :
return 0
left_value = self.maxValue(root.left)
right_value = self.maxValue(root.right)
value1 = root.val
value2 = root.val + left_value
value3 = root.val + right_value
value4 = root.val + left_value + right_value
#以此节点为根节点的最大值
max_value = max([value1, value2, value3, value4])
self.res = max(self.res, max_value)
#要和父节点关联,则需要取去除情况4的最大值 也是要返回的关联值
return max([value1, value2, value3])
在上文之上可以简化答案:
# 在上文的基础上 简化
def maxValue(self, root):
if not root :
return 0
# 对左子树以及右子树的 最小值做了限定 即 左右子树的结果都是>=0 的 因此也不需要再对 value1 2 3 4 判断大小 必然是value4最大
left_value = max(0, self.maxValue(root.left))
right_value = max(0, self.maxValue(root.right))
self.res = max(self.res, root.val+left_value+right_value)
实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 true
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/implement-trie-prefix-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
什么是前缀树(字典树):
Trie树其实就是维护有公共前缀子串的树
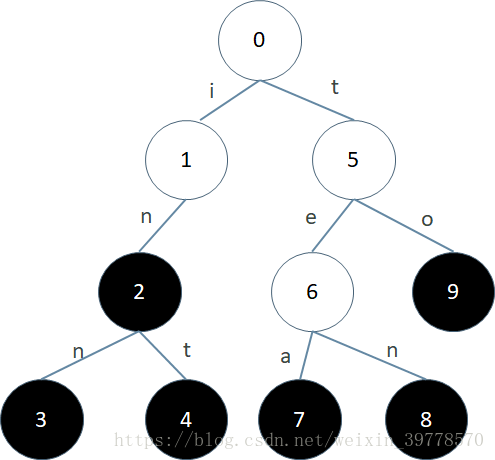
链接 : https://blog.csdn.net/weixin_39778570/article/details/81990417
上面这棵Trie树包含的字符串集合是{in, inn, int, tea, ten, to}
前缀树的操作主要有 插入以及搜索两种功能
实现前缀树的几个主要功能 插入 搜索 以及判断前缀,依据python来写十分简单,但还是注意一下,后续还有类似问题
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.lookup = {}
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
tree = self.lookup
for i in word:
if i not in tree:
tree[i] = {}
#无论通过与否,都要挪到下一部分
tree = tree[i]
#需要增加一个结束的标志位
tree["#"] = "#"
def search(self, word: str) -> bool:
"""
Returns if the word is in the trie.
"""
tree = self.lookup
for i in word:
if i not in tree:
return False
tree = tree[i]
if "#" in tree:
return True
return False
def startsWith(self, prefix: str) -> bool:
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
tree = self.lookup
for i in prefix:
if i not in tree:
return False
tree = tree[i]
return True
-
注意二叉树是递归型数据结构,所以很多时候可以用到递归的方法 ---------非常常见的方法 十分重要
-
数据结构 之 二叉搜索树 可以看看这个简书 https://www.jianshu.com/p/ff4b93b088eb
-
二叉树遍历 https://www.cnblogs.com/anzhengyu/p/11083568.html 深度优先DFS(先序 中序 后序) 广度优先BFS 层次遍历
-
二叉树遍历使用栈非递归方式迭代的内在思想:
- 因为要在遍历完节点的左子树后接着遍历节点的右子树,为了能找到该节点,需要使用栈来进行暂存 同时也有先进后出的味道在。中序和后序也都涉及到回溯,所以都需要用到栈。 要去遍历右节点 所以需要保存下来分支的节点 https://www.jianshu.com/p/456af5480cee 可以查看一些详细的注释 核心思想为: 1 将待处理的点入栈,从这个结点开始进行后续遍历(因此在栈不空的时候,表明本棵树没有处理完) 2 疯狂向左走,直到走不动 3 当前面临的点是左边没得走了。看看能不能向右走(分两种1 右边空或右边已经处理过 2 右边有的走,走到右边,再回到2)
- 每拿到一个 节点 就把它保存在 栈 中
- 继续对这个节点的 左子树 重复 过程1,直到左子树为 空
- 因为保存在 栈 中的节点都遍历了 左子树 但是没有遍历 右子树,所以对栈中节点 出栈 并对它的 右子树 重复 过程12 直到遍历完所有节点
作者:18211010139 链接:https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/die-dai-jie-fa-shi-jian-fu-za-du-onkong-jian-fu-za/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
层次遍历错误 出现了问题 这层还没遍历完呢 就在stack中加入了下一层的元素 导致混乱 是 stack list出现了问题 deque 的 append() 和 popleft() 函数
层次遍历之后 直接比较数组元素 最后2^(n-1) 个元素是否前后对称
cur, stack = root, []
ans = []
while cur or stack:
ans.append(cur.val)
print(ans)
if cur.left:
stack.append(cur.left)
if cur.right:
stack.append(cur.right)
cur = stack[::-1].pop()
print(ans)
特点: 对于树中每个节点:
- 若其左子树存在,则其左子树中每个节点的值都不大于该节点值;
- 若其右子树存在,则其右子树中每个节点的值都不小于该节点值。
性质: 其元素大小的性质 使得 对二叉搜索树进行中序遍历(左中右),即可得到有序数组