不用额外空间意味着只能在原地操作,而在原地操作需要注意不能影响到还未计算的部分。
基本思路:把已经计算过的部分视为新数组,在这部分里面操作不会影响到后面的结果。
这题不能直接套优先队列(堆)模板,因为这里面的pop_front是要返回原队列的头部,不是优先队列的头部(max/min)。但是max_value又需要在O(1)内完成查询,所以只用一个队列肯定不行。
于是我们需要用到一个神奇的辅助队列sort_queue,它的头部就是max_value。
- 如何维护
sort_queue? - 原始队列发生
pop_front时sort_queue该怎么变动?
只会做背包类dp的我笑了
延伸阅读:背包九讲
一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过根结点。
遍历每一个节点计算它的深度及经过它的最大直径长度
直径长度=左孩子深度+右孩子深度-根节点深度*2
depth[lchild]+depth[rchild]-depth[node]*2]
是上一题的进阶版
跟上一题不一样,路径长度可能负值,所以遍历每个节点的时候不能直接算以当前节点为根节点的子树的所有路径长度之和。
如果左子树或右子树路径长度之和小于零就要舍去。
最长路径有三种情况:
a.father
\
a
/ \
b c
- b->a->c
- a.father->a->b
- a.father->a->c
递归的时候怎么写呢?
def dfs(root: TreeNode) -> int:
nonlocal max_path_sum
if root is None:
return 0
left_val = max(0, dfs(root.left))
right_val = max(0, dfs(root.right))
node_val = max(left_val, right_val)+root.val
max_path_sum = max(max_path_sum, left_val+right_val+root.val)
return node_val为什么只用max_path_sum = max(max_path_sum, left_val+right_val+root.val)就可以取三种情况中的最大值?
注意到return node_val = max(left_val, right_val)+root.val,以上面为例子,dfs(a.father)=max(a.father->a->b,a.father->a->c)实际上在上一层递归中已经计算了三种情况中的后两种,所以只需要计算第一种即可。
不要用脑子套进去一层层计算,要相信dfs(a)返回的就是a的node_val,不需要管里面的一层套一层的逻辑,只需要写好其中一层的逻辑,它自然就能够跑起来
求两个字符串的最大公因子
十分有趣的一道题,求两个数的最大公因子自然用欧几里得算法
def gcd(a,b):
if a<b:
a,b=b,a
if b==0:
return a
gcd(b,a%b)那求两个字符串该怎么办呢?
一个很棒的题解
-
判断是否有解
str1+str2=str2+str1 -
有解的话最大公因子的长度是不是两个字符串长度的gcd?
是的,因为如果能循环以它的约数为长度的字符串,自然也能够循环以它为长度的字符串,所以这个理论长度就是我们要找的最优解。
pairing阶段:两个不同选票的人进行对抗,并会同时击倒对方,当剩下的人都是同一阵营,相同选票时,结束。
counting阶段:计数阶段,对最后剩下的下进行选票计算统计,判断选票是否超过总票数的一半,选票是否有效。
这题有很多种做法:
- 排序后中间元素即为众数
- hashtable存储
- 随机选取并验证
- 分治
- 摩尔投票法
上一题是选一个代表,这题是选两个代表
本质是选票抵消,但是需要注意代码逻辑
(但是我还是不会怎么买卖股票)
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
如果你最多只允许完成一笔交易(即买入和卖出一支股票)
max(price[i]-price[j]) (i>j)
你可以尽可能地完成更多的交易(多次买卖一支股票)
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
贪心:当前策略总是全局最佳策略
今天比昨天高就买,否则不买
你最多可以完成两笔交易
遍历划分点,把数组分成两部分,分别计算两部分的最大利润,相当于第一题
但是直接算会超时,这里用一个小优化,提前算好从左边到划分点的最大利润left_max和从有右边到划分点的最大利润right_max
算right_max时注意要逆向思考,记录的是max_price
class Solution:
def maxProfit(self, prices) -> int:
if not prices:
return 0
# left_max: [0,i] max profit
left_max = [0] * len(prices)
min_price = prices[0]
for i in range(1, len(prices)):
min_price = min(min_price, prices[i])
left_max[i] = max(left_max[i - 1], prices[i] - min_price)
# right_max: [i,len-1] max profit
right_max = [0] * len(prices)
max_price = prices[-1]
for i in range(len(prices)-2, -1, -1):
max_price = max(max_price, prices[i])
right_max[i] = max(right_max[i + 1], max_price-prices[i])
max_profit = 0
for i in range(0, len(prices)):
max_profit = max(max_profit, left_max[i]+right_max[i])
return max_profitf[i][j][k]表示第i天,进行了j次交易,当前状态为k时的最大利润
该题中$j<=2$
k=0表示没有持有股票,k=1表示持有股票
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0])
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1])
f[i][0][0] = 0
f[i][0][1] = -inf
f[0][i][0] = -inf
f[0][i][1] = -inf
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int maxProfit(vector<int> &prices)
{
const int inf = 1 << 30;
const int n = prices.size();
int f[30000 + 5][3][2];
for (int i = 0; i <= n; i++)
{
f[i][0][0] = 0;
f[i][0][1] = -inf;
}
for (int i = 1; i <= 2; i++)
{
f[0][i][0] = -inf;
f[0][i][1] = -inf;
}
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= 2; j++)
{
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0]);
if (j)
{
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1]);
}
}
}
return max(max(f[n][0][0], f[n][1][0]), f[n][2][0]);
}
};你最多可以完成 k 笔交易
这道题就用通解
注意当k>=n的时候转化为第二题的情况,直接用贪心算法。不然时间和空间都会爆炸的。
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int maxProfit(int k, vector<int> &prices)
{
const int inf = 1 << 30;
const int n = prices.size();
// 用贪心处理能随意买卖的情况
if (k >= n)
{
int profit = 0;
for (int i = 1; i < n; i++)
{
if (prices[i] > prices[i - 1])
{
profit += prices[i] - prices[i - 1];
}
}
return profit;
}
int f[n + 5][k + 1][2];
for (int i = 0; i <= n; i++)
{
f[i][0][0] = 0;
f[i][0][1] = -inf;
}
for (int i = 1; i <= k; i++)
{
f[0][i][0] = -inf;
f[0][i][1] = -inf;
}
for (int i = 1; i <= n; i++)
{
for (int j = 0; j <= k; j++)
{
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0]);
if (j)
{
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1]);
}
}
}
int maxProfit = 0;
for (int i = 0; i <= k; i++)
maxProfit = max(maxProfit, f[n][i][0]);
return maxProfit;
}
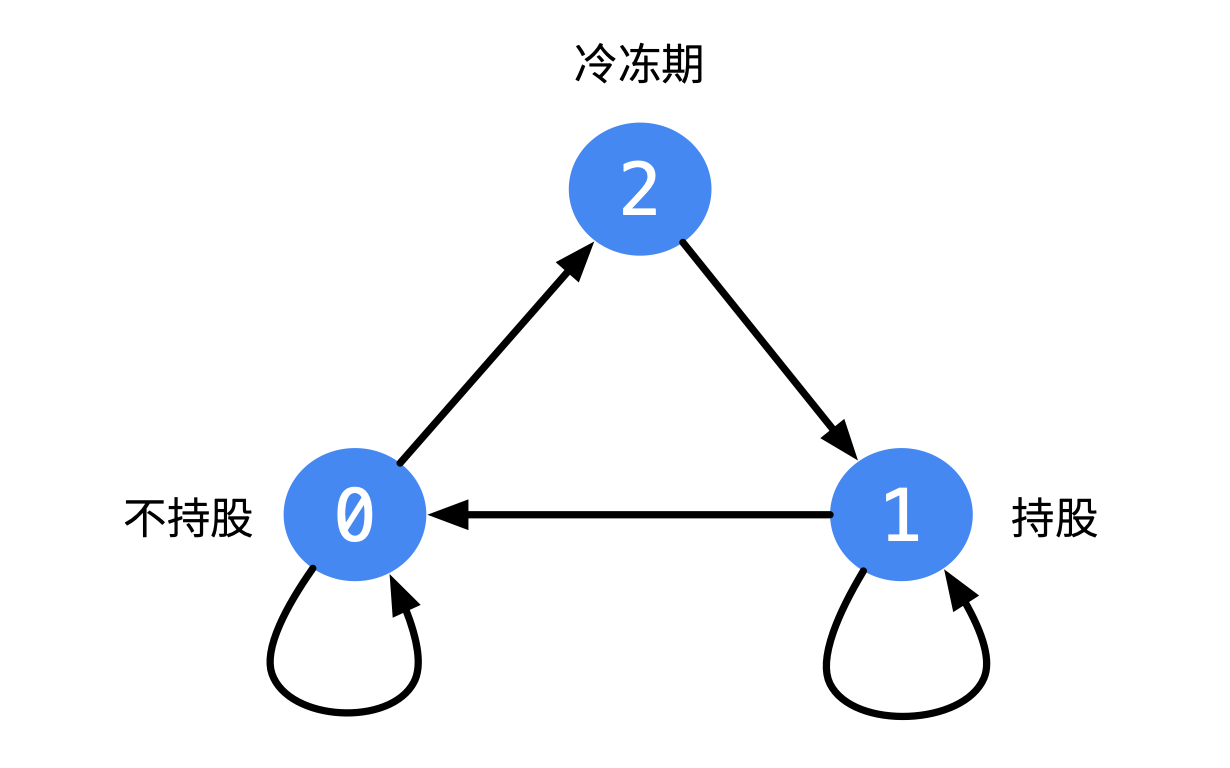
};卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
无限制交易次数
状态转移方程要改一改
原来的:
f[i][j][0] = max(f[i - 1][j][1] + prices[i - 1], f[i - 1][j][0])
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - prices[i - 1])
现在要把第二维状态压掉并改一下卖股票的那条方程,相当于要过两天才能收到卖股票的钱
f[i][0] = max(f[i - 2][1] + prices[i - 2], f[i - 1][0]);
f[i][1] = max(f[i - 1][1], f[i - 1][0] - prices[i - 1]);
还要判断一下边界,因为如果最后一天卖出的话,就会收不到钱
f[n + 1][0] = max(f[n - 1][1] + prices[n - 1], f[n][0]);
return max(f[n + 1][0], f[n][0]);
class Solution
{
public:
int maxProfit(vector<int> &prices)
{
const int inf = 1 << 30;
const int n = prices.size();
if (!n){
return 0;
}
int f[n + 5][2];
for (int i = 0; i <= n + 1; i++)
{
f[i][0] = 0;
f[i][1] = -inf;
}
for (int i = 1; i <= n; i++)
{
if (i >= 2)
{
f[i][0] = max(f[i - 2][1] + prices[i - 2], f[i - 1][0]);
}
f[i][1] = max(f[i - 1][1], f[i - 1][0] - prices[i - 1]);
}
f[n + 1][0] = max(f[n - 1][1] + prices[n - 1], f[n][0]);
return max(f[n + 1][0], f[n][0]);
}
};再加上滚动变量
int f[3];
f[0] = 0;
f[1] = -inf;
f[2] = 0;
int preCash = f[0];
int preStock = f[1];
for (int i = 1; i <= n; i++)
{
f[0] = max(preCash, preStock + prices[i - 1]);
f[1] = max(preStock, f[2] - prices[i - 1]);
f[2] = preCash;
preCash = f[0];
preStock = f[1];
}
return max(f[0], f[2]);你可以无限次地完成交易,但是你每次交易都需要付手续费。
改一点点就可以了,买的时候把fee减掉
f[i][1] = max(f[i - 1][1], f[i - 1][0] - prices[i - 1]-fee);
压缩状态,当前状态只依赖于上一状态
class Solution
{
public:
int maxProfit(vector<int> &prices, int fee)
{
const int inf = 1 << 30;
const int n = prices.size();
if (n <= 1)
{
return 0;
}
int f[2][2];
f[0][0] = 0;
f[0][1] = -inf;
for (int i = 1; i <= n; i++)
{
f[i&1][0] = max(f[i - 1&1][1] + prices[i - 1], f[i - 1&1][0]);
f[i&1][1] = max(f[i - 1&1][1], f[i - 1&1][0] - prices[i - 1] - fee);
}
return f[n&1][0];
}
};dfs+回溯
从第一行开始放,一直放到最后一行
用四个bool数组判断行,列,左对角线,右对角线有没有皇后
dfs出来记得把状态恢复原位
CSC1001 Assignment2
找到一个直接exit()
先上代码
#include <iostream>
using namespace std;
class Solution
{
public:
int ans = 0;
int full;
void dfs(int col, int leftdown, int rightdown)
{
if (col == full) //每一列都已经有皇后了,说明满了
{
++ans;
return;
}
// col|leftdown|rightdown 任何一个是1都不行,表示在皇后攻击范围内
// 取反后,1是可以放的位置,0是不能放的
// 与 11111(n个1)与运算后把高位舍去,剩下的位数为棋盘的边长
int now = full & ~(col | leftdown | rightdown);
while (now)
{
// 取最低一位1,表示在这里放一个皇后
int lowbit = now & -now;
now -= lowbit;
// 更新3个状态
// row是没有用的,因为row已经包含在col里面了
// col=col+lowbit
// leftdown=(leftdown+lowbit)<<1
// rightdown=(rightdown+lowbit)>>1
dfs(col + lowbit, (leftdown + lowbit) << 1, (rightdown + lowbit) >> 1);
}
}
int totalNQueens(int n)
{
full = (1 << n) - 1;
dfs(0, 0, 0);
return ans;
}
};一种非常牛逼的解法,需要有高超的位运算能力。
简单来说,就是把原来的4个bool数组压缩成了3个int数,用这三个数的每一位表示约束条件。
因为不需要输入方案,只求方案个数,所以不需要存储之前的皇后位置。
1表示在皇后的攻击范围里面
0表示可以放皇后
n=5
full=2^5-1=31=11111
5个1表示放满了
取二进制数的最低位
在while里面起到遍历当前行所有能放皇后的位置
lowbit(x)=x&-x
这个最容易理解,如果某一位上是1,就说明之前在这列上有皇后。
位数对应列数
假设现在dfs到第三行,前面两行的皇后分别放在第一和第四列
1 0 0 0
0 0 0 1
1 0 0 1
col=1001
右上到左下的对角线,加上当前行的皇后位置后,整体左移一位
dfs到第三行
0 0 1 0
1 0 0 0
1 1 0 0 0
leftdown=11000
实际上最高位的1被舍去了,因为有full&
左上到右下的对角线,加上当前行的皇后位置后,整体右移一位
0 1 0 0
0 0 0 1
0 0 0 1 1
rightdown=00011
实际上最右侧的1被舍去了,位运算的overflow
Lis[i]表示以nums[i]为结尾的最长上升序列的长度
Lis[i]=max(Lis[j]+1) j<i and nums[j]<nums[i]
Lis[]存储当前的最长上升序列
如果当前的数比Lis中最后一位还要大,Lis[++ans]=nums[i]
如果小的话,就在Lis数组(单调递增)中二分查找大于等于nums[i]的第一个数
class Solution
{
public:
int lengthOfLIS(vector<int> &nums)
{
int Lis[10005];
if (nums.size() <= 1)
{
return nums.size();
}
Lis[1] = nums[0];
int ans = 1;
for (int i = 1; i < nums.size(); i++)
{
if (nums[i] > Lis[ans])
{
Lis[++ans] = nums[i];
continue;
}
int left = 1, right = ans;
while (left < right)
{
int mid = (left + right) >> 1;
if (Lis[mid] >= nums[i])
{
right = mid;
}
else
{
left = mid + 1;
}
}
Lis[left] = nums[i];
}
return ans;
}
};说实话,这题想了挺久的,也调了很久。
与求LIS的O(n^2)算法类似,多维护一个MaxLength[]数组,记录到当前位置LIS的长度
j<i && nums[j]<nums[i]
// Lis[i] == Lis[j] + 1 说明之前已经找到长度为Lis[i]的LIS了 现在还有一种方案,于是将两种方案数相加
if (Lis[i] == Lis[j] + 1)
{
MaxLength[i] += MaxLength[j];
}
// Lis[i] < Lis[j] + 1 说明之前没有找到LIS,直接将方案数转移
else if (Lis[i] < Lis[j] + 1)
{
Lis[i] = Lis[j] + 1;
MaxLength[i] = MaxLength[j];
}class Solution
{
public:
int findNumberOfLIS(vector<int> &nums)
{
int Lis[10005];
int MaxLength[10005];
if (nums.size() <= 1)
{
return nums.size();
}
int LisLength = 1;
int ans = 0;
for (int i = 0; i < nums.size(); i++)
{
MaxLength[i] = 1;
Lis[i] = 1;
}
for (int i = 0; i < nums.size(); i++)
{
for (int j = 0; j < i; j++)
{
if (nums[i] <= nums[j])
{
continue;
}
if (Lis[i] == Lis[j] + 1)
{
MaxLength[i] += MaxLength[j];
}
else if (Lis[i] < Lis[j] + 1)
{
Lis[i] = Lis[j] + 1;
MaxLength[i] = MaxLength[j];
}
}
// 一边遍历一遍维护答案
if (Lis[i] > LisLength)
{
LisLength = Lis[i];
ans = MaxLength[i];
}
else if (Lis[i] == LisLength)
{
ans += MaxLength[i];
}
}
return ans;
}
};小优化:不需要用额外的bool数组记录是否访问过,直接将访问过的陆地变为水就可以了。
注意area的计算,每次dfs到下一个点,都要更新area的值并返回给上一个点,这样就能保证dfs入口处返回的area是总的大小
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class Solution
{
public:
int maxArea = 0;
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int dfs(vector<vector<int>> &grid, int row, int col, int area)
{
grid[row][col] = 0;
for (int i = 0; i < 4; i++)
{
int nxtRow = row + dir[i][0];
int nxtCol = col + dir[i][1];
if (nxtRow < 0 || nxtRow >= grid.size() || nxtCol < 0 || nxtCol >= grid[0].size())
continue;
if (grid[nxtRow][nxtCol])
{
area = dfs(grid, nxtRow, nxtCol, area + 1);
}
}
return area;
}
int maxAreaOfIsland(vector<vector<int>> &grid)
{
for (int i = 0; i < grid.size(); i++)
{
for (int j = 0; j < grid[i].size(); j++)
{
if (grid[i][j])
{
maxArea = max(dfs(grid, i, j, 1), maxArea);
}
}
}
return maxArea;
}
};比上一题简单一点,只需要记录dfs了多少次即可,不需要求面积。
int maxAreaOfIsland(vector<vector<int>> &grid)
{
for (int i = 0; i < grid.size(); i++)
{
for (int j = 0; j < grid[i].size(); j++)
{
if (grid[i][j])
{
maxArea = max(dfs(grid, i, j, 1), maxArea);
}
}
}
return maxArea;
}