好题!
给你一个字符串 s ,请你返回满足以下条件的最长子字符串的长度:每个元音字母,即 'a','e','i','o','u' ,在子字符串中都恰好出现了偶数次。
一开始我是暴力搜索的,从[0,len-1]出发,每次让左端点加一或者右端点减一,显然这样做会超时
class Solution
{
public:
const char vowel[5] = {'a', 'e', 'i', 'o', 'u'};
int count[6];
int ans;
void find(int l, int r, string &s)
{
if (l > r)
return;
bool flag = 1;
for (int i = 0; i < 5; i++)
{
if (count[i] % 2 != 0)
{
flag = 0;
break;
}
}
if (flag)
ans = max(ans, r - l + 1);
int tmp = 5;
for (int i = 0; i < 5; i++)
{
if (s[l] == vowel[i])
{
--count[i];
tmp = i;
break;
}
}
find(l + 1, r, s);
++count[tmp];
tmp = 5;
for (int i = 0; i < 5; i++)
{
if (s[r] == vowel[i])
{
--count[i];
tmp = i;
break;
}
}
find(l, r - 1, s);
++count[tmp];
}
int findTheLongestSubstring(string s)
{
for (auto each : s)
{
for (int i = 0; i < 5; i++)
{
if (each == vowel[i])
{
++count[i];
break;
}
}
}
find(0, s.size() - 1, s);
return ans;
}
};看了下提示,要用到bitmask和prefix sum,再结合题目“恰好出现了偶数次”的提示,不难想到要用异或来表示字符串的状态。
那就用每一位分别表示每一个元音字母出现的次数呗,1表示出现次数为奇数,0表示出现次数为偶数
前缀和是这样推想出来的:
aaee 00000
aee 00001
a 00001
sum["aee"]=sum["aaee"]^sum["a"]
sum[1,3]=sum[3]^sum[0]
类比sum[1,3]=sum[3]-sum[0],用前缀和求[1,3]的区间和
那现在我们要求:
sum[1,3]=0
即sum[3]^sum[0]=0
根据异或的交换律
sum[3]^0=sum[0]
等价于sum[3]=sum[0]
于是问题转化为:在所有[l,r]区间中,求满足sum[r]=sum[l-1]的最大区间。
后面我没有想到哈希表的方法,暴力应该过不了,所以偷偷看了评论
原理其实很简单:
- 如果当前的状态没有出现过,就把它加到哈希表里面
- 如果出现过,就计算区间长度,并维护
ans最大区间长度
状态只有1<<5=32个,所以可用数组来代替unordered_map
两个易错点:
- 哈希表里面记录的是
sum[l-1]第一次出现的位置,计算区间长度时需要注意len=r-hash_map[state]对应len=r-(l-1)=r-l+1 - 边界问题,如果最长字符串是从下标
0开始,即l=0,l-1=-1,所以初始化m[1...31]=-2,-2表示状态还未出现过,m[0]=-1,表示空字符串对应的状态为00000
这真的是一道middle题吗?建议大家认真消化知识点
class Solution {
public:
const char vowel[5] = {'a', 'e', 'i', 'o', 'u'};
int findTheLongestSubstring(string s)
{
int m[32];
int state=0;
int ans=0;
for (int i=0;i<32;i++)
m[i]=-2;
m[0]=-1;
for (int j=0;j<s.size();j++)
{
for (int i=0;i<5;i++)
{
if (s[j]==vowel[i])
{
state^=(1<<i);
break;
}
}
if (m[state]!=-2)
ans=max(ans,j-m[state]);
else
m[state]=j;
}
return ans;
}
};二进制浮点数表示:
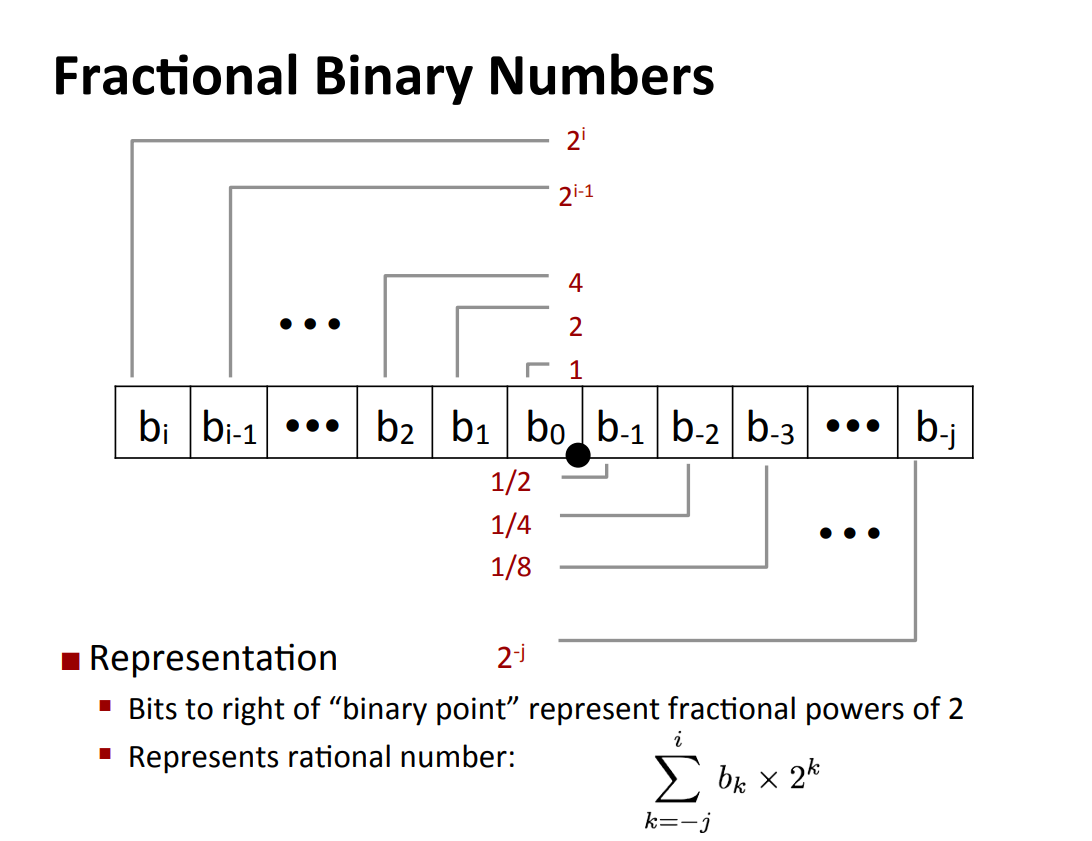
$$ \sum^i_{k=-j}b_k*2^k $$
$>>1=/2$ $<<1=*2$
- Can only exactly represent numbers of the form
$x/2^k$ - 小数部分会占用整数部分的位数(在位数有限情况下)
- Numerical Form:
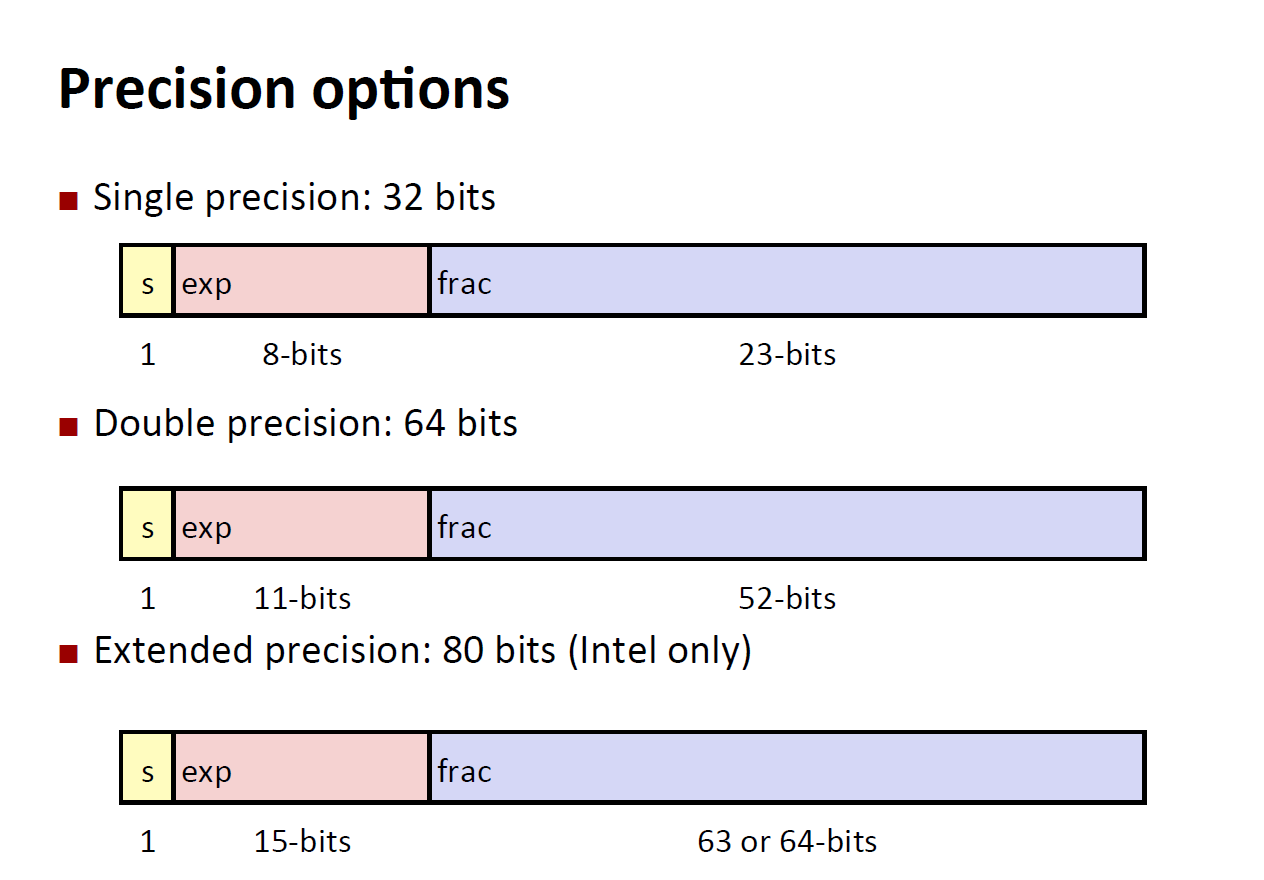
$$ (-1)^sM2^E $$
-
$s$ is sign bit $M\in[1.0,2.0)$ - Exponent
$E$
-
- Encoding
- e.g.
- Rounding
- Violates associativity
- Overflow and inexactness of rounding
-
$(3.14+1e10)-1e10=10$ ,$3.14+(1e10-1e10)=3.14$
- Violates distributivity
- Conversions
- double/float->int
- Like rounding towards 0
- double的整数部分比int的多
- int->double exact
- int->float rounding
- double/float->int
这场错过了,没有打实况。
一道有点像俄罗斯方块的题目,已知俄罗斯方块游戏结束时的图案,求各个块落下的顺序
Apollo is playing a game involving polyominos. A polyomino is a shape made by joining together one or more squares edge to edge to form a single connected shape. The game involves combining N polyominos into a single rectangular shape without any holes. Each polyomino is labeled with a unique character from A to Z.
Apollo has finished the game and created a rectangular wall containing R rows and C columns. He took a picture and sent it to his friend Selene. Selene likes pictures of walls, but she likes them even more if they are stable walls. A wall is stable if it can be created by adding polyominos one at a time to the wall so that each polyomino is always supported. A polyomino is supported if each of its squares is either on the ground, or has another square below it.
Apollo would like to check if his wall is stable and if it is, prove that fact to Selene by telling her the order in which he added the polyominos.
我的想法是模拟+dfs:
- 维护一个集合$S={当前可以放下的形状}$
- dfs遍历$S$并维护
supported数组(表示合法的放置位置)
写了一个多小时,才把样例过了...,然而一个测试集都没过
Google的题还是挺需要转化的,这题其实不需要模拟。
每一个小块的落下要求:
- 它在底部
- 它的正下方已经有小块了
所以对于1~(n-1)的列,上下两个小块之间存在约束关系。我们可以用有向图来存储这种约束关系。每一对的约束关系都满足的条件下,能否找到一个合法的遍历这个图的序列。
显然,当图中存在环时不合法:
A<-->B
要放A就要先放B
要放B就要先放A
于是都放不了
用拓扑排序来判断有向图中有没有环,并得到拓扑序即为答案
题意很简单,求一个数组中,子数组(数组中连续元素组成)的和为完全平方数的个数。
第一个测试集N=1000可以直接暴力判断,我学到了一个新函数modf
double res = sqrt(sum[i] - sum[j - 1]);
double f;
if (modf(res, &f) == 0.0)
++ans;第二个测试集n=1e5肯定不能暴力了,怎么办呢?
那就看题解吧,反正想不出来了
题解确实很巧妙:
- 注意到每个数组元素$A_i\in[-100,100]$,用类似于计数排序的方法,哈希表
m[x]存储到当前元素为止,前缀和等于x的子数组个数 - 枚举的时候,第二层枚举可能的完全平方数,用逆向思维求$[1,i]$内以
A[i]结尾的,和为完全平方数的子数组个数$[1,i]=[1,k]+[k+1,i]$。我们不知道有多少个$sum[k+1,i]=完全平方数$,但是我们知道$[1,k]=sum[1,i]-完全平方数$的个数
int sum[100005];
void solve()
{
int n;
cin >> n;
ll ans = 0;
unordered_map<int, int> num_prefix_sum;
int minx = 0;
for (int i = 1; i <= n; i++)
{
int res;
cin >> res;
sum[i] = sum[i - 1] + res;
minx = min(minx, sum[i]);
}
num_prefix_sum[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = 0;; j++)
{
int tmp = sum[i] - j * j;
if (tmp < minx)
break;
if (num_prefix_sum.count(tmp))
ans += num_prefix_sum[sum[i] - j * j];
}
num_prefix_sum[sum[i]]++;
}
cout << ans << endl;
}来体验一下打CF的感觉
https://blog.csdn.net/Fiveneves/article/details/106294338
Polycarp wants to buy exactly n shovels. The shop sells packages with shovels. The store has k types of packages: the package of the i-th type consists of exactly i shovels (1≤i≤k). The store has an infinite number of packages of each type.
Polycarp wants to choose one type of packages and then buy several (one or more) packages of this type. What is the smallest number of packages Polycarp will have to buy to get exactly n shovels?
For example, if n=8 and k=7, then Polycarp will buy 2 packages of 4 shovels.
Help Polycarp find the minimum number of packages that he needs to buy, given that he:
will buy exactly n shovels in total; the sizes of all packages he will buy are all the same and the number of shovels in each package is an integer from 1 to k, inclusive.
题意还是很简单的:从$[1,k]$中找出最大的x,使$n%x==0$,$ans=n/x$
但是我卡了很久也没有做出来
找一个数的因数嘛,我就想到用质数表了,$\sqrt{1e9}\approx31700$范围也不大,算法伪代码如下:
for prime in [2,sqrt(n)]:
if n%prime==0 and n/prime<=k:
return prime
枚举$n$的质因子,找到最小的满足条件的质因子就是答案了
但是这里其实有不少问题:
- 这个满足条件的质因子可能大于$\sqrt{n}$
- 答案不一定是一个质数
for (int i = 1; i <= maxdiv; i++)
{
if (n % i == 0)
{
if (i <= k)
ans = min(ans, n / i);
if (n / i <= k)
ans = min(ans, i);
}
}遍历$[1,\sqrt{n}]$,找$[1,\sqrt{n}]$的ans和$(\sqrt{n},n]$范围内的ans:
- 如果
i是ans,我们找的是最小的ans,同时需要满足每一份的大小n/i<=k - 如果
i是每一份的大小n/ans,i=n/ans<=k,份数ans=n/i