参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
-
示例 1:
-
输入:[7,1,5,3,6,4]
-
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。 -
示例 2:
-
输入:prices = [7,6,4,3,1]
-
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
《代码随想录》算法视频公开课:动态规划之 LeetCode:121.买卖股票的最佳时机1,相信结合视频再看本篇题解,更有助于大家对本题的理解。
这道题目最直观的想法,就是暴力,找最优间距了。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int result = 0;
for (int i = 0; i < prices.size(); i++) {
for (int j = i + 1; j < prices.size(); j++){
result = max(result, prices[j] - prices[i]);
}
}
return result;
}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
当然该方法超时了。
因为股票就买卖一次,那么贪心的想法很自然就是取最左最小值,取最右最大值,那么得到的差值就是最大利润。
C++代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int low = INT_MAX;
int result = 0;
for (int i = 0; i < prices.size(); i++) {
low = min(low, prices[i]); // 取最左最小价格
result = max(result, prices[i] - low); // 直接取最大区间利润
}
return result;
}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][0] 表示第i天持有股票所得最多现金 ,这里可能有同学疑惑,本题中只能买卖一次,持有股票之后哪还有现金呢?
其实一开始现金是0,那么加入第i天买入股票现金就是 -prices[i], 这是一个负数。
dp[i][1] 表示第i天不持有股票所得最多现金
注意这里说的是“持有”,“持有”不代表就是当天“买入”!也有可能是昨天就买入了,今天保持持有的状态
很多同学把“持有”和“买入”没区分清楚。
在下面递推公式分析中,我会进一步讲解。
- 确定递推公式
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
- 第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]
那么dp[i][0]应该选所得现金最大的,所以dp[i][0] = max(dp[i - 1][0], -prices[i]);
如果第i天不持有股票即dp[i][1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
- 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的,dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
这样递推公式我们就分析完了
- dp数组如何初始化
由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出
其基础都是要从dp[0][0]和dp[0][1]推导出来。
那么dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
- 确定遍历顺序
从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的,那么一定是从前向后遍历。
- 举例推导dp数组
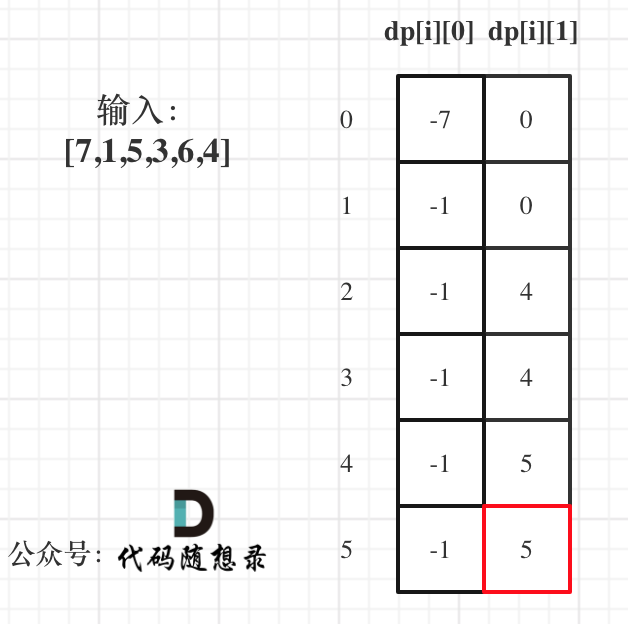
以示例1,输入:[7,1,5,3,6,4]为例,dp数组状态如下:
dp[5][1]就是最终结果。
为什么不是dp[5][0]呢?
因为本题中不持有股票状态所得金钱一定比持有股票状态得到的多!
以上分析完毕,C++代码如下:
// 版本一
class Solution {
public:
int maxProfit(vector<int>& prices) {
int len = prices.size();
if (len == 0) return 0;
vector<vector<int>> dp(len, vector<int>(2));
dp[0][0] -= prices[0];
dp[0][1] = 0;
for (int i = 1; i < len; i++) {
dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
}
return dp[len - 1][1];
}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
从递推公式可以看出,dp[i]只是依赖于dp[i - 1]的状态。
dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
那么我们只需要记录 当前天的dp状态和前一天的dp状态就可以了,可以使用滚动数组来节省空间,代码如下:
// 版本二
class Solution {
public:
int maxProfit(vector<int>& prices) {
int len = prices.size();
vector<vector<int>> dp(2, vector<int>(2)); // 注意这里只开辟了一个2 * 2大小的二维数组
dp[0][0] -= prices[0];
dp[0][1] = 0;
for (int i = 1; i < len; i++) {
dp[i % 2][0] = max(dp[(i - 1) % 2][0], -prices[i]);
dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);
}
return dp[(len - 1) % 2][1];
}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
这里能写出版本一就可以了,版本二虽然原理都一样,但是想直接写出版本二还是有点麻烦,容易自己给自己找bug。
所以建议是先写出版本一,然后在版本一的基础上优化成版本二,而不是直接就写出版本二。
Java:
贪心法:
class Solution {
public int maxProfit(int[] prices) {
// 找到一个最小的购入点
int low = Integer.MAX_VALUE;
// res不断更新,直到数组循环完毕
int res = 0;
for(int i = 0; i < prices.length; i++){
low = Math.min(prices[i], low);
res = Math.max(prices[i] - low, res);
}
return res;
}
}动态规划:版本一
// 解法1
class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) return 0;
int length = prices.length;
// dp[i][0]代表第i天持有股票的最大收益
// dp[i][1]代表第i天不持有股票的最大收益
int[][] dp = new int[length][2];
int result = 0;
dp[0][0] = -prices[0];
dp[0][1] = 0;
for (int i = 1; i < length; i++) {
dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
}
return dp[length - 1][1];
}
}动态规划:版本二(使用二維數組(和卡哥思路一致),下面還有使用一維滾動數組的更優化版本)
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
int dp[][] = new int[2][2];
dp[0][0] = - prices[0];
dp[0][1] = 0;
for (int i = 1; i < len; i++){
dp[i % 2][0] = Math.max(dp[(i - 1) % 2][0], - prices[i]);
dp[i % 2][1] = Math.max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);
}
return dp[(len - 1) % 2][1];
}
}动态规划:版本二(使用一維數組)
class Solution {
public int maxProfit(int[] prices) {
int[] dp = new int[2];
// 记录一次交易,一次交易有买入卖出两种状态
// 0代表持有,1代表卖出
dp[0] = -prices[0];
dp[1] = 0;
// 可以参考斐波那契问题的优化方式
// 我们从 i=1 开始遍历数组,一共有 prices.length 天,
// 所以是 i<=prices.length
for (int i = 1; i <= prices.length; i++) {
// 前一天持有;或当天买入
dp[0] = Math.max(dp[0], -prices[i - 1]);
// 如果 dp[0] 被更新,那么 dp[1] 肯定会被更新为正数的 dp[1]
// 而不是 dp[0]+prices[i-1]==0 的0,
// 所以这里使用会改变的dp[0]也是可以的
// 当然 dp[1] 初始值为 0 ,被更新成 0 也没影响
// 前一天卖出;或当天卖出, 当天要卖出,得前一天持有才行
dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);
}
return dp[1];
}
}Python:
贪心法:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
low = float("inf")
result = 0
for i in range(len(prices)):
low = min(low, prices[i]) #取最左最小价格
result = max(result, prices[i] - low) #直接取最大区间利润
return result动态规划:版本一
class Solution:
def maxProfit(self, prices: List[int]) -> int:
length = len(prices)
if len == 0:
return 0
dp = [[0] * 2 for _ in range(length)]
dp[0][0] = -prices[0]
dp[0][1] = 0
for i in range(1, length):
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0])
return dp[-1][1]动态规划:版本二
class Solution:
def maxProfit(self, prices: List[int]) -> int:
length = len(prices)
dp = [[0] * 2 for _ in range(2)] #注意这里只开辟了一个2 * 2大小的二维数组
dp[0][0] = -prices[0]
dp[0][1] = 0
for i in range(1, length):
dp[i % 2][0] = max(dp[(i-1) % 2][0], -prices[i])
dp[i % 2][1] = max(dp[(i-1) % 2][1], prices[i] + dp[(i-1) % 2][0])
return dp[(length-1) % 2][1]动态规划:版本三
class Solution:
def maxProfit(self, prices: List[int]) -> int:
length = len(prices)
dp0, dp1 = -prices[0], 0 #注意这里只维护两个常量,因为dp0的更新不受dp1的影响
for i in range(1, length):
dp1 = max(dp1, dp0 + prices[i])
dp0 = max(dp0, -prices[i])
return dp1Go:
贪心法:
func maxProfit(prices []int) int {
min := prices[0]
res := 0
for i := 1; i < len(prices); i++ {
if prices[i] - min > res {
res = prices[i]-min
}
if min > prices[i] {
min = prices[i]
}
}
return res
}动态规划:版本一
func maxProfit(prices []int) int {
length := len(prices)
if length == 0{return 0}
dp := make([][]int,length)
for i := 0; i < length; i++ {
dp[i] = make([]int, 2)
}
dp[0][0] = -prices[0]
dp[0][1] = 0
for i := 1; i < length; i++ {
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
}
return dp[length-1][1]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}动态规划:版本二
func maxProfit(prices []int) int {
dp := [2][2]int{}
dp[0][0] = -prices[0]
dp[0][1] = 0
for i := 1; i < len(prices); i++ {
dp[i%2][0] = max(dp[(i-1)%2][0], -prices[i])
dp[i%2][1] = max(dp[(i-1)%2][1], dp[(i-1)%2][0]+prices[i])
}
return dp[(len(prices)-1)%2][1]
}
func max(a, b int) int {
if a > b{
return a
}
return b
}JavaScript:
动态规划
const maxProfit = prices => {
const len = prices.length;
// 创建dp数组
const dp = new Array(len).fill([0, 0]);
// dp数组初始化
dp[0] = [-prices[0], 0];
for (let i = 1; i < len; i++) {
// 更新dp[i]
dp[i] = [
Math.max(dp[i - 1][0], -prices[i]),
Math.max(dp[i - 1][1], prices[i] + dp[i - 1][0]),
];
}
return dp[len - 1][1];
};贪心法
var maxProfit = function(prices) {
let lowerPrice = prices[0];// 重点是维护这个最小值(贪心的思想)
let profit = 0;
for(let i = 0; i < prices.length; i++){
lowerPrice = Math.min(lowerPrice, prices[i]);// 贪心地选择左面的最小价格
profit = Math.max(profit, prices[i] - lowerPrice);// 遍历一趟就可以获得最大利润
}
return profit;
};TypeScript:
贪心法
function maxProfit(prices: number[]): number {
if (prices.length === 0) return 0;
let buy: number = prices[0];
let profitMax: number = 0;
for (let i = 1, length = prices.length; i < length; i++) {
profitMax = Math.max(profitMax, prices[i] - buy);
buy = Math.min(prices[i], buy);
}
return profitMax;
};动态规划
function maxProfit(prices: number[]): number {
/**
dp[i][0]: 第i天持有股票的最大现金
dp[i][1]: 第i天不持有股票的最大现金
*/
const length = prices.length;
if (length === 0) return 0;
const dp: number[][] = [];
dp[0] = [-prices[0], 0];
for (let i = 1; i < length; i++) {
dp[i] = [];
dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
}
return dp[length - 1][1];
};C#:
贪心法
public class Solution
{
public int MaxProfit(int[] prices)
{
int min = Int32.MaxValue;
int res = 0;
for (int i = 0; i < prices.Length; i++)
{
min = Math.Min(prices[i], min);
res = Math.Max(prices[i] - min, res);
}
return res;
}
}动态规划
public class Solution
{
public int MaxProfit(int[] prices)
{
int[] dp = new int[2];
int size = prices.Length;
(dp[0], dp[1]) = (-prices[0], 0);
for (int i = 0; i < size; i++)
{
dp[0] = Math.Max(dp[0], -prices[i]);
dp[1] = Math.Max(dp[1], dp[0]+prices[i]);
}
return dp[1];
}
}Rust:
贪心
impl Solution {
pub fn max_profit(prices: Vec<i32>) -> i32 {
let (mut low, mut res) = (i32::MAX, 0);
for p in prices {
low = p.min(low);
res = res.max(p - low);
}
res
}
}动态规划
impl Solution {
pub fn max_profit(prices: Vec<i32>) -> i32 {
let mut dp = vec![-prices[0], 0];
for p in prices {
dp[0] = dp[0].max(-p);
dp[1] = dp[1].max(dp[0] + p);
}
dp[1]
}
}