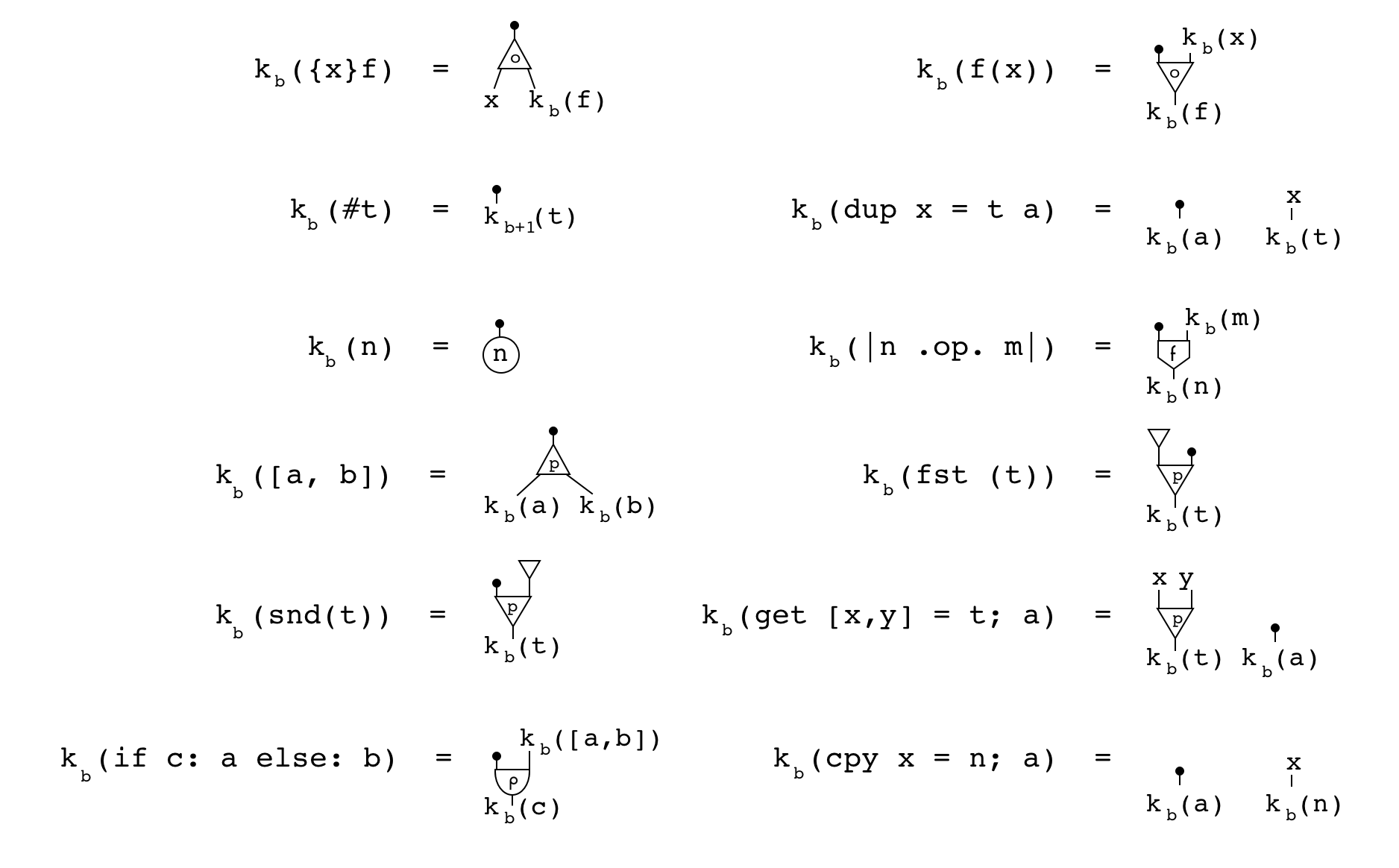Skip to content

Latest commit

 

History

History
698 lines (552 loc) · 33.3 KB

README.md

File metadata and controls

698 lines (552 loc) · 33.3 KB
Raw

Moonad: a Peer-to-Peer Operating System

Victor Maia, John Burnham

Abstract.

We present Moonad, a peer-to-peer operating system. Its machine language, FM-Net, consists of a massively parallel, beta-optimal graph-reduction system based on interaction nets. Moonad's purely functional user-facing language, Formality features a powerful, elegant type-system capable of stating and proving theorems about its own programs through inductive λ-encodings. Online interactions are made through Trellis, a global append-only event-log compatible with both trusted and decentralized backends. On top of those, we build a front-end interface, Moonad, where users can create, deploy and use decentralized applications (Forall), pose and solve mathematical problems (Provit), and exchange scarce virtual assets (Phos).

Table of Contents

  • Introduction

  • Formality: An efficient functional programming and proof language

  • FM-Net: A parallel low-level machine language

  • Trellis: A public append-only event-log

  • Moonad: An operating system

Introduction

Computing is a field in its infancy. While humans have performed manual computation with fingers, pencil, abacus or quipu since time immemorial, it has been only 75 years since the first general-purpose computing machine was switched on. Given how ubiquitous computers are in our lives today, it can be easy to forget this, but there are hundreds of millions still living who are older than the computer. If a generation in human terms is 25 years, computers users today are at most third-generation.

Accordingly, it should not be surprising that computing systems we use in practice -devices, operating systems, programming languages- lag behind (sometimes far behind) theoretical or experimental systems. Consider that the most popular operating system in the world, Android was designed in the late 2000s, based on a kernel from the 1990s (Linux), which itself was based on a design from the 1970s. There simply hasn't been enough time for all the good ideas to be discovered and to percolate into common use.

For example, most electronic authentication on the web is still done with passwords (sometimes stored in plain-text!), despite the fact that this contributes to tens of billions of dollars lost per year to identity theft and that secure systems for authentication based on public key cryptography have existed for at least the past 30 years.

In a related area, most electronic commerce is mediated by centralized trusted counterparties, despite the fact that this regularly leads to data breaches that compromise the security of millions of people. Decentralized systems, such cryptographic ledgers using byzantine-fault-tolerant chains of signed transactions and trustless distributed computing platforms have been under intense development for the better part of the past decade, but have yet to gain widespread adoption.

There has been tremendous theoretical progress in programming language and compiler design, that is barely exploited. We have substructural type systems that can eliminate resource management errors (like segmentation faults) and ensure memory safety. We have proof languages capable of unifying the field of mathematics and programming as one (the Curry-Howard correspondence). In principle, we could have systems software that is formally proven to be error-free, and proof assistants that are both user-friendly enough to be taught in grade-school math class and performant enough to be used on any platform.

Contrast this theoretical progress with our practical record: not long ago, we had a single, small malicious package cause the entire web ecosystem to collapse, twice. More than 300,000 sites online today are vulnerable to SQL injections. Bugs like heartbleed and TheDAO cause enormous monetary losses. A single CPU exploit slowed down nearly every processor in the world by 30%. Faulty software kills people, routinely causing airplanes to crash and hospitals to stop operating.

We believe this mismatch between theory and practice is due to presentation: The technology exists, we need to build the user experience.

Moonad aims to assemble many of these amazing technologies into a decentralized operating system that "just works". We aim to use type theory to build computing systems that are safer, faster and friendlier.

Formality: An efficient functional programming and proof language

The Curry-Howard correspondence states that there is a structural congruence between computer programs and proofs in formal logic. While in theory this implies that software developers and mathematicians are engaged in substantially the same activity, in practice there are many barriers preventing the unification of the two fields. Programming languages with type systems expressive enough to take advantage of Curry-Howard, such as Haskell, Agda and Coq generally have substantial runtime overhead, which makes them challenging to use, particularly at the systems programming level. On the other hand, systems languages such as Rust, Nim or ATS, have shown that type systems can greatly enhance usability and correctness of low-level software, but either have type systems too weak to fully exploit Curry-Howard (Rust, Nim), or introduce syntactic complexity that limits adoption (ATS). In other words, there are lots of slow languages with great type systems and lots of fast languages with lousy type systems.

As programmers and as mathematicians, we don't want to compromise. On one side, mathematicians have the power of rigor: there is nothing more undeniably correct than a mathematical proof. Yet ironically, those proofs are often written, checked and reviewed by humans in an extremely error-prone process. On the other side, programmers have the power of automation: there is nothing more capable of performing a huge set of tasks without making a single mistake than a computer program. Yet, equally ironically, most of those programs are written in an unrigorous, bug-ridden fashion. Formality lies in the intersection between both fields: it is a programming language in which developers are capable of implementing everyday algorithms and data structures, but it is also a proof language, on which mathematicians are capable of proposing and proving theorems.

Formality's types can be seen as a language of specifications that can be mechanically checked by the compiler, allowing you to enforce arbitrary guarantees on your program's behavior. For example, in an untyped language, you could write an algorithm such as:

// Returns the element at index `idx` of an array `arr`
function get_at(i, arr) {
  ... code here ...
}

But this has no guarantees. You could call it with nonsensical arguments such as get_at("foo", 42), and the compiler would do nothing to stop you, leading to (possibly catastrophical) runtime errors. Traditional typed languages improve the situation, allowing you to "enrich" that definition with simple or even polymorphic types, such as:

function get_at<A>(i : Num, arr : Array<A>) : A {
  ... code here ...
}

This has some guarantees. For example, it is impossible to call get_at with a String index, preventing a wide class of runtime errors. But you can still, for example, call get_at with an index out of bounds. In fact, a similar error caused the catastrophic heartbleed vulnerability. Formality types are arbitrarily expressive, allowing you to capture all demands you'd expect from get_at:

get_at*L : {A: Type, i: Fin(L), arr: Vector(A, L)} -> [x: A ~ At(A,L,i,arr,x)]
  ... code here ...

Here, we use a bound, L, to enforce that the index is not larger than the size of the array, and we also demand that the returned element, x: A, is exactly the one at index i. This specification is complete, in the mathematical sense. It is not only impossible to get a runtime error by calling get_at, but it is also impossible to write get_at incorrectly to begin with. Note that this is different from, for example, asserts or bound checking. Here, the compiler statically reasons about the flow or your program, assuring that it can't go wrong with zero runtime costs.

In a similar fashion, you could use types to ensure that the balance of a smart-contract never violates certain invariants, or that an airplane controller won't push its nose down to a crashing position. Of course, you don't need to write types so precise. If your software doesn't demand security, you could go all way down to having fully untyped programs. The point is that the ability of expressing properties so precisely is immensely valuable, especially when developing critical software that demands all the security one can afford.

Some readers might object here that while formal proofs can ensure that a program's implementation matches its specification, it cannot eliminate errors inherent to the specification. This is true, but, in many cases, specifications are much smaller than implementations. For example,

spec : Type
  [
    // Demands a List function such that
    sort : List(Word) -> List(Word),

    // It returns the same list in ascendinig order
    And(is_same(xs, sort(ys)), is_ascending(sort(ys)))
  ]

The spec above demands a List function such that it returns the same list in ascending order. Writing and auditing this specification is considerably easier than implementing a complete sort function. As such, formal verification can be seen as an optimization of human auditing: instead of verifying a vast amount of code, you audit a small specification and let the compiler do the rest.

An accessible syntax

Proof languages often have complex syntaxes that make them needlessly inaccessible, as if the subject wasn't hard enough already. Coq, for example, uses 3 different languages with different rules and an overall heavy syntax. Agda is clean and beautiful, but relies heavily on unicode and agda-mode, making it essentially unusable outside of EMACs, which is arguably a "hardcore" editor. Formality aims to keep a simple, familiar syntax that is much closer to common languages like Python and JavaScript.

// A natural number is either `zero` or the successor of a natural number
T Nat
| succ {pred : Nat}
| zero

// A vector is a list with a statically known length
T Vector {A : Type} (len : Nat)
| vcons {len : Nat, head : A, tail : Vector(A, len)} (succ(len))
| vnil                                               (zero)

// A type-safe "head" that returns the first element of a non-empty vector
// - On the `vcons` case, return the vector's head
// - On the `vnil` case, prove it is unreachable, since `xs.len > 0`
vhead : {~T : Type, ~n : Nat, xs : Vector(T, succ(n))} -> T
  case/Vector xs
  note e : xs.len is succ(n)
  | vcons => xs.head
  | vnil  => absurd(zero_isnt_succ(~n, ~e), ~T) 
  : T

Our goal is for a regular TypeScript developer to be able to read e.g. our Functor formalization without too much effort:

T Functor {F : Type -> Type}
| functor 

  // A mapping function
  { map : {~A : Type , ~B : Type , f : A -> B, x : F(A)} -> F(B)

  // Satisfying the identity law
  , identity : {~A : Type , fa : F(A)} -> map(~A, ~A, id(~A),fa) == fa

  // Satisfying the composition law
  , composition :
      { ~A : Type, ~B : Type, ~C : Type, g : B -> C, f : A -> B, fa : F(A)
      } -> map(~A, ~C, {x} g(f(x)), fa) == map(~B, ~C, g, map(~A, ~B, f, fa))

  }

While we may not be quite there, we're making fast progress towards that goal.

Fast and portable "by design"

Some languages are inherently slow, by design. JavaScript, for example, is slower than C: all things equal, its mandatory garbage collector will be an unavoidable disadvantage. Even C, arguably the fastest modern language, has its flaws, as its ultra-sequential model of computation has hit a hard barrier. Formality is meant to be as fast as theoretically possible. For example, it has affine lambdas, allowing it to be garbage-collection-free. It has a strongly confluent interaction-net runtime, allowing it to be evaluated in massively parallel architectures. It is a functional language that doesn’t require bruijn bookkeeping, making it the fastest “closure chunker” around. It is lazy, has a clear cost model for blockchains and a minuscule (448 LOC) runtime, making it extremely portable.

If we designed our operating system using a language like C, it'd be fast today, but, on the long-term, it would become obsolete. Instead, we decided to rely on a new model of computation that isn't as fast today, since it is competing against decades of optimizations, but that has the best computational characteristics imaginable, making it extremely future-proof and giving it a virtually unbounded room for improvements. In other words, Formality is fast "by design".

An optimal high-order evaluator

Formality's substitution algorithm is asymptotically faster than Haskell's, Clojure's, JavaScript's and other closure implementations. This makes it extremely fast at evaluating high-order programs, combining a Haskell-like high-level feel with a Rust-like low-level performance curve. For example, Haskell's stream fusion, a hard-coded, important optimization, happens naturally, at runtime, on Formality. This also allow us to explore new ways to develop algorithms, such as this "impossibly efficient" exp-mod implementation implementation. Who knows if this may lead to new breakthroughs in complexity theory?

Guaranteed termination

All programs written in Formality are guaranteed to halt, and enjoy key computational characteristics that differ from classic functional languages. This directly enables many runtime features and optimizations (such as no book-keeping), although without loss of generality as Formality can model Turing-Complete programs via corecursion. In other words, Turing-Complete computation can be performed by writing an iteration step function in Formality and either looping this function infinitely in your runtime system, or folding this function over a Church number representing a finite bound on the computation.

We view this design decision as a principled acknowledgement that in practice no real software is truly Turing-Complete; actual physical systems can only be finite state machines.

An elegant underlying Type Theory

Formality's unique approach to termination is conjectured to allow it to have elegant, powerful type-level features that would be otherwise impossible without causing logical inconsistencies. For example, instead of built-in datatypes, we rely on Self Types, which allow us to implement inductive families with native lambdas. As history tells, having elegant foundations often pays back. We've not only managed to port several proofs from other assistants, but found techniques to emulate Coq's structural recursion, to perform large eliminations, and even an hypothetical encoding of higher inductive types; and we've barely began exploring the system.

FM-Net: a massively parallel, low-level machine language

Interaction Net (inet) simulation

Formality terms are compiled to a memory-efficient interaction net system called FM-Net. Interaction nets are graphs where nodes have labeled ports, one being the main one, plus a list of "rewrite rules" that are activated whenever two nodes are connected by their main ports. A simple interaction-net graph-rewrite system called "interaction combinators" with only 3 symbols and 6 rules was shown to be a universal model of [computation][2]. As a universal mode, interaction-nets combine many useful properties of other models such as Turing machines and the lambda calculus. Like Turing machines, interactions-nets can be evaluated as a series of atomic, local operations with a clear physical implementation. Like the lambda calculus, interaction-nets are inherently parallel, but in a more robust manner, admitting desirable computational properties such as strong confluence, optimal sharing and zero-cost garbage-collection.

We use a slightly modified version of interaction combinators, called FM-Net as our lowest-level machine language, extending interaction combinators with additional graph node types for efficient numeric operations. Our implementation has advantages over previous interaction net graph-reduction systems (such as the Bologna Optimal Higher-order Machine) in that it requires no book-keeping, requires only 128 bits per lambda or pair, has unboxed 32-bit integers and constant-time beta reduction. This is possible due to Formality's stratification, a structural discipline on how terms are duplicated, inherited from its underlying logic, Elementary Affine.

Node Types

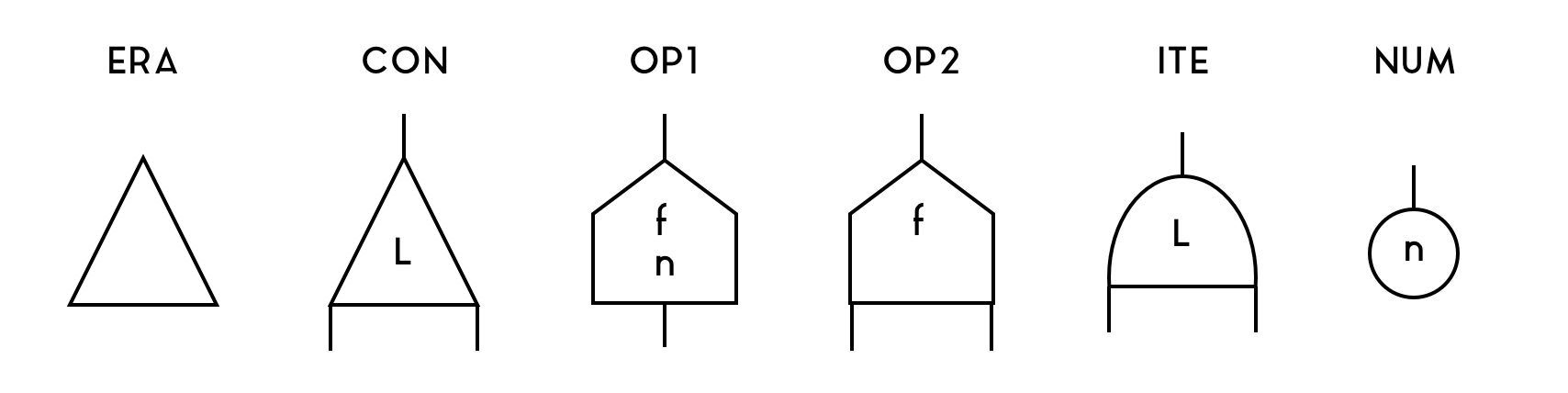
Our FM-Net system includes 6 types of nodes, ERA, CON, OP1, OP2, ITE, NUM.

  • CON has 3 ports and an integer label. It is used to represent lambdas, applications, boxes (implicitly) and duplications. Just CON is enough for beta-reduction.

  • ERA has 1 port and is used to free empty memory, which happens when a function that doesn't use its bound variable is applied to an argument.

  • NUM has 1 port and stores an integer and is used to represent native numbers.

  • OP1 has 2 ports and stores one integer and an operation id. OP2 has 3 ports and an operation id. They are used for numeric operations such as addition and multiplication.

  • ITE has 3 ports and an integer label. It is used for if-then-else, and is required to enable number-based branching.

Note that the position of the port matters. The port on top is called the main port. The first port counter-clockwise to the main port (i.e., to the left on this drawing) is the aux0 port, and the first port clockwise to the main port (i.e., to the right on this drawing) is the aux1 port.

Rewrite rules

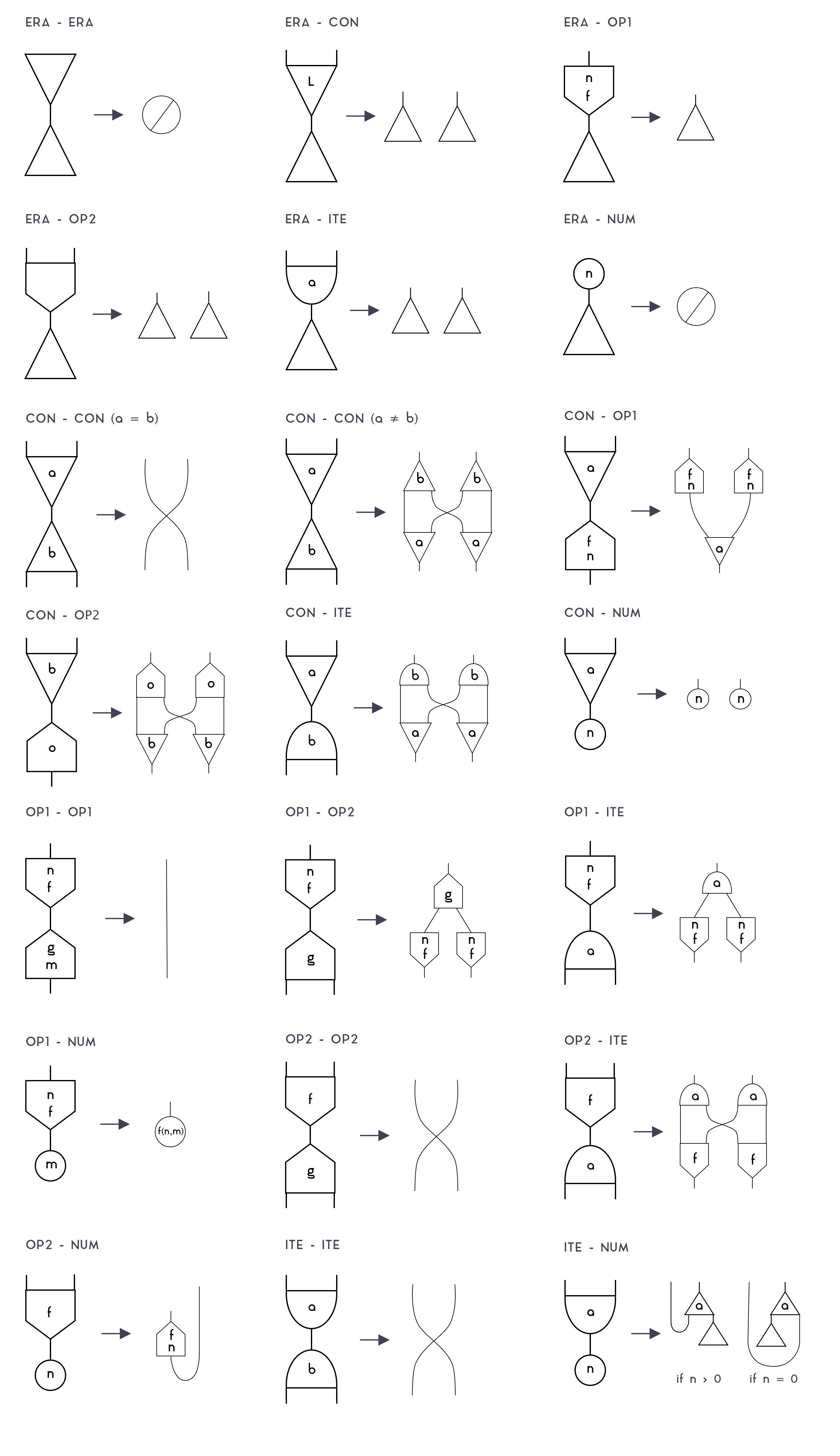
In order to perform computations, FM-Net has a set of rewrite rules that are triggered whenever two nodes are connected by their main ports. This is an extensive list of those rules:

Note that, while there are many rules (since we need to know what to do on each combination of a node), most of those have the same "shape" (such as OP2-OP2, ITE-ITE), so they can reuse the same code. There are only 5 actually relevant rules:

  • Erasure: When an ERA or a NUM node collides with anything, it "destroys" the other node, and propagates itself to destroy all nodes connected to it.

  • Substitution: When two CON nodes of equal label collide, and also on the OP2-OP2 / ITE-ITE cases, both nodes are destroyed, and their neighbors are connected. That's the rule that performs beta-reduction because it allows connecting the body of a lambda (which is represented with CON) to the argument of an application (which is, too, represented with CON). Note that on the OP2-OP2 and ITE-ITE cases, that's just a default rule that doesn't matter, since those cases can't happen on valid Formality programs.

  • Duplication: When different nodes collide, they "pass through" each other, duplicating themselves in the process. This allows, for example, CON nodes with a label >1 to be used to perform deep copies of any term, with dup x = val; .... It can copy lambdas and applications because they are represented with CON nodes with a label 0, pairs and pair-accessors, because they are represented with CON nodes with a label 1, and ITE, OP1, OP2, because they are different nodes.

    It also allows duplications to duplicate terms that are partially duplicated (i.e., which must duplicate, say, a λ-bound variable), as long as the CON labels are different, otherwise, the CON nodes would instead fall in the substitution case, destroying each other and connecting neighbors, which isn't correct. That's why FMC's box system is necessary: to prevent concurrent duplication processes to interfere with each other by ensuring that, whenever you duplicate a term with dup x = val; ..., all the duplication CON nodes of val will have a labels higher than the one used by that dup.

  • If-Then-Else When an ITE node collides with a NUM node, it becomes a CON node with one of its ports connected to an ERA node. That's because then/else branches are actually stored in a pair, and this allows you to select either the fst or the snd value of that pair and discard the other branch.

  • Num-Operation When OP2 collides with a NUM, it becomes an OP1 node and stores the number inside it; i.e., the binary operation becomes a unary operation with NUM partially applied. When that OP1 collides with another NUM, then it performs the binary operation on both operands, and return a new NUM with the result. Those rules allow us to add, multiply, divide and so on native numbers.

Compiling Formality terms to FM-Net

The process of compiling Formality terms to FM-Net can be defined by the following function k_b(net):

This function recursively walks through a term, creating nodes and "temporary variables" (x_b) in the process. It also keeps track of the number of boxes it passed through, b. For example, on the lambda ({x}f) case, the procedure creates a CON node with a label 0, creates a "temporary variable" x_b on the aux0 port, recurses towards the body of the function, f on the aux1 port, and then returns the main port (because there is a black ball on it). Notice that there isn't a case for VAR. That's what those "temporary variables" are for. On the VAR case, two things can happen:

  1. If the corresponding "temporary variable" x_b was never used, simply return a pointer to it.

  2. If the corresponding "temporary variable" x_b was used, create a "CON" node with a label 2 + b, connect its main port to the old location of x_b, its aux0 to the port x_b pointed to, and return a pointer to its aux1 port.

This process allows us to create as many CON nodes as needed to duplicate dup-bound variables, and labels those nodes with the layer of that dup (plus 2, since labels 0 and 1 are used for lambdas/applications and pairs/projections). Note that this process is capable of duplicating λ-bound variables, but this isn't safe in practice, and won't happen in well-typed inputs.

Implementation

In our implementation, we use a buffer of 32-bit unsigned integers to represent nodes, as follows:

  • CON: represented by 4 consecutive uints. The first 3 represent the main, aux0 and aux1 ports. The last one represents the node type (2 bits), whether its ports are pointers or unboxed numbers (3 bits), and the label (27 bits).

  • OP1: represented by 4 consecutive uints. The first 2 represent the main and aux0 ports. The third represents the stored number. The last one represents the node type (2 bits), whether its ports are pointers or unboxed numbers (3 bits, 1 unused), and the operation (27 bits).

  • OP2: represented by 4 consecutive uints. The first 3 represent the main, aux0 and aux1 ports. The last one represents the node type (2 bits), whether its ports are pointers or unboxed numbers (3 bits), and the operation (27 bits).

  • ITE: represented by 4 consecutive uints. The first 2 represent the main, aux0 and aux1 ports. The third represents the stored number. The last one represents the node type (2 bits), whether its ports are pointers or unboxed numbers (3 bits), and the label (27 bits).

  • ERA: is stored inside other nodes and do not use any extra space. An ERA node is represented by a pointer port which points to itself. That's because ERA's rewrite rules coincide with what we'd get if we allowed ports to point to themselves.

  • NUM: is stored inside other nodes and do not use any extra space. A NUM node is represented by a numeric port. In order to know if a port is a number or a pointer, each node reserves 3 bits of its last uint to store that information.

Rewrites

TODO: explain how rewrite works, how link_ports is used, and why unlink_ports is necessary to avoid invalid states.

Strict evaluation

The strict evaluation algorithm is very simple. First, we must keep a set of redexes, i.e., nodes connected by their main ports. In order to do that, whenever we link two main ports, we must add the address of the smallest nodes to that set. We then perform a loop to rewrite all redexes. This will give us a new set of redexes, which must then be reduced again, over and over, until there are no redexes left. This is the pseudocode:

while (len(net.redexes) > 0):
  for redex in net.redexes:
    net.rewrite(redex)

The strict reduction is interesting because it doesn't require graph walking nor garbage collection passes, and because the inner for-loop can be performed in parallel. That is, every redex in net.redexes can be rewritten at the same time.

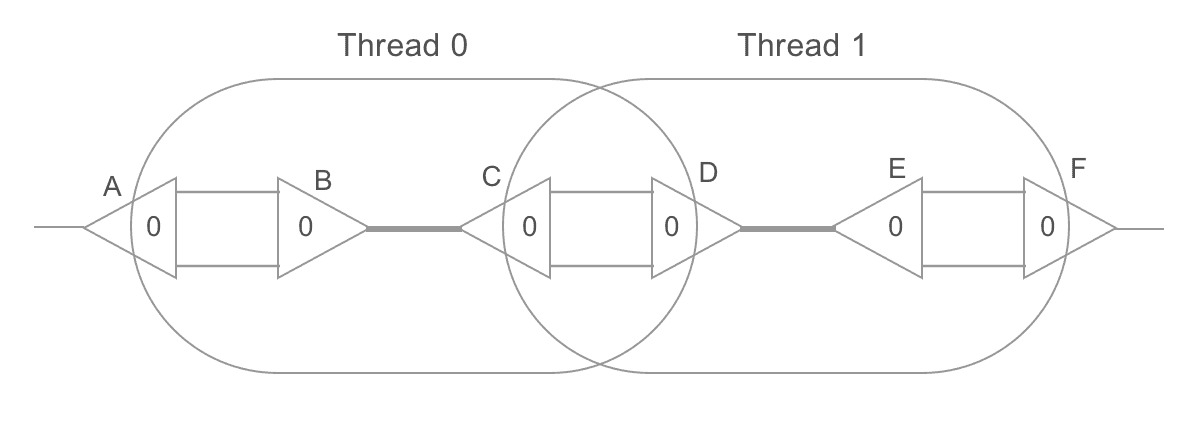
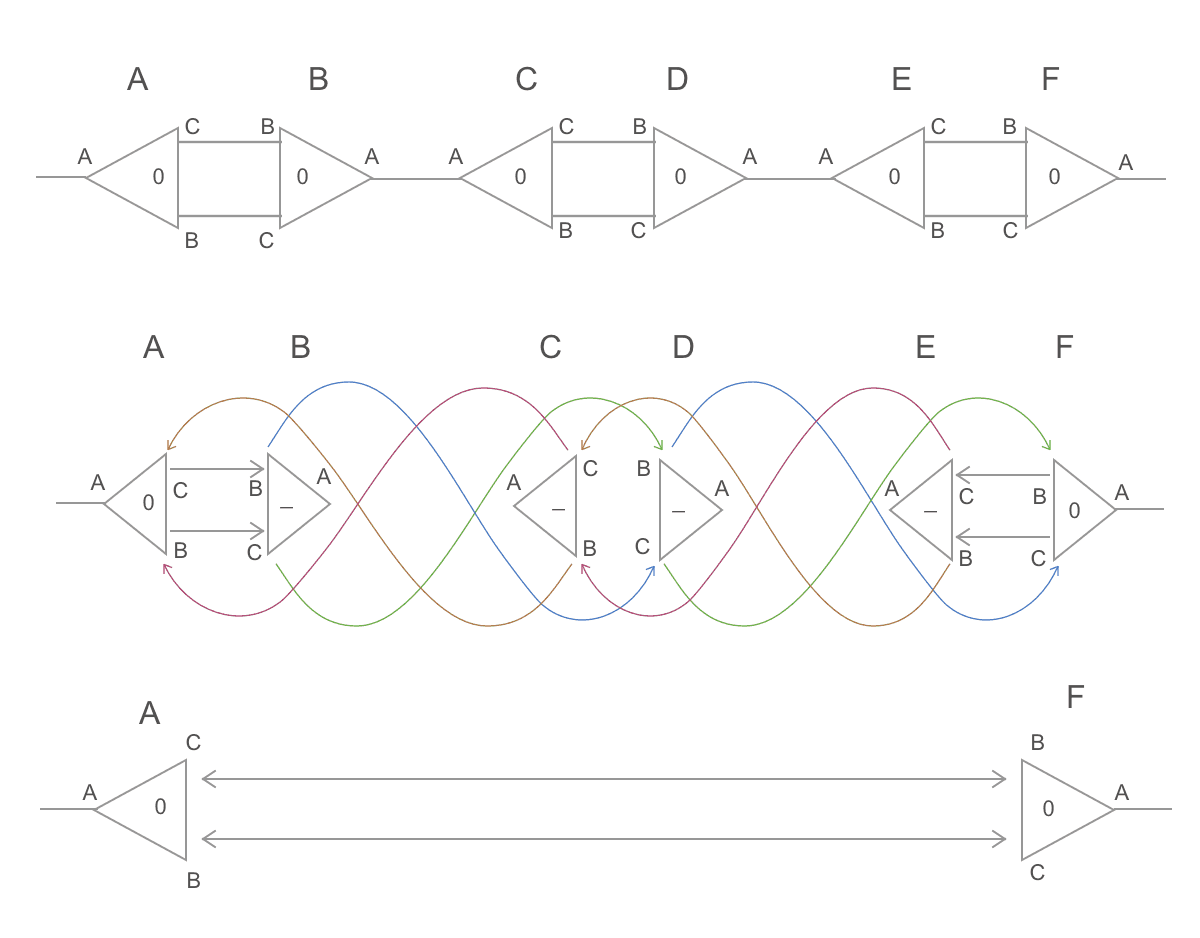
In order to do that, though, one must be cautious with intersection areas. For example, in the graph below, B-C and D-E are redexes. If we reduce them in parallel, both threads will attempt to read/write from C's and D's aux0 and aux1 ports, potentially causing synchronization errors.

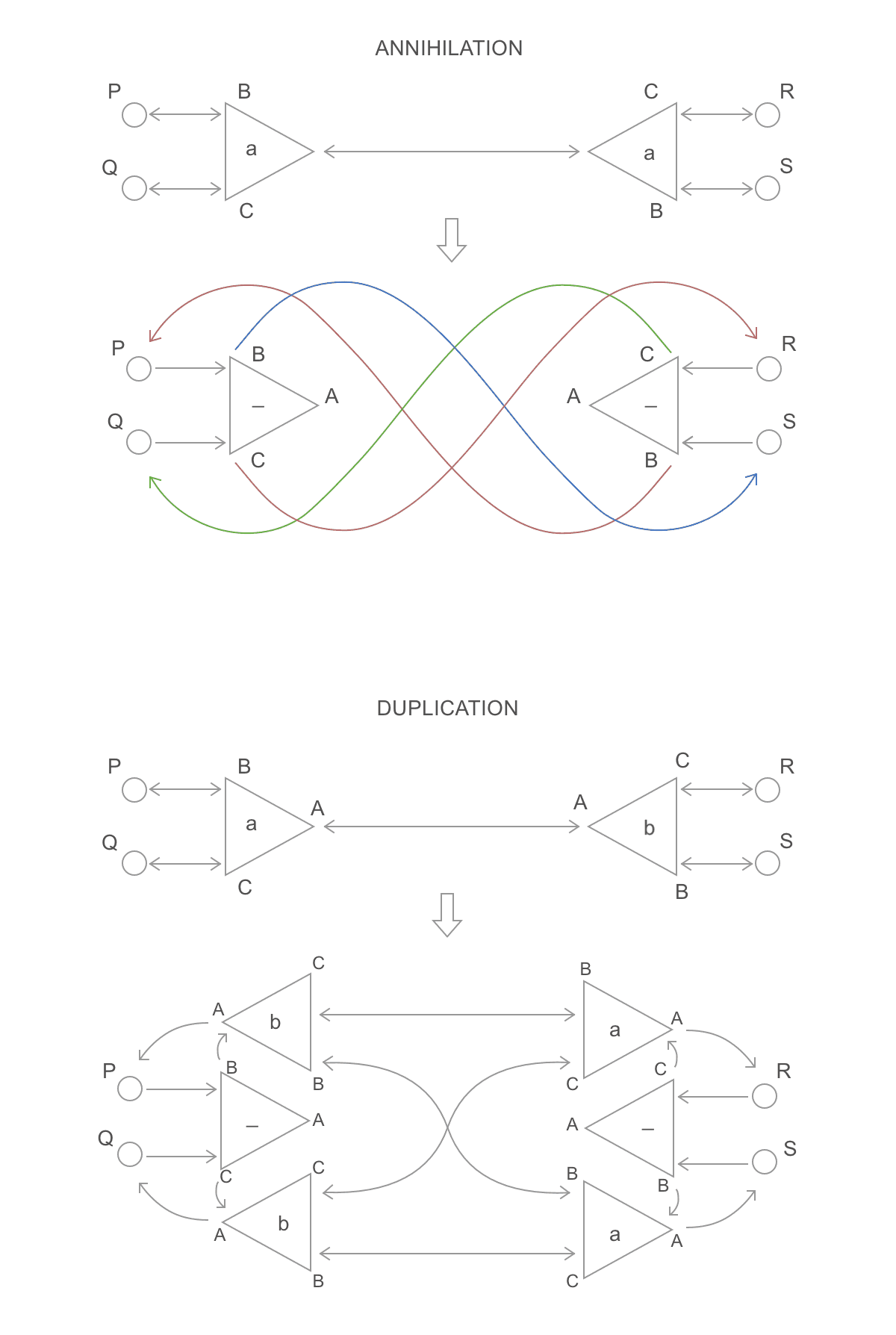
This can be avoided through locks, or by performing rewrites in two steps. On the first step, each thread reads/writes the ports of its own active pair as usual, except that, when it would need to connect a neighbor, it instead turns its own node into a "redirector" which points to where the neighbor was supposed to point. For example, substitution and duplication would be performed as follows:

Notice that P, Q, R and S (neighbor ports) weren't touched: they keep pointing to the same ports, but now those ports point to where they should point to. Then, a second parallel step is performed. This time, we spawn a thread for each neighbor port and walk through the graph until we find a non-redirector node. We then point that neighbor to it. Here is a full example:

Notice, for example, the port C of the node A. It is on the neighborhoods of a redex (B-C), but isn't a redex itself. On the first step, two threads rewrite the nodes B-C and D-E, turning them into redirectors, and without touching that port. On the second step, a thread starts from port C of node A, towards port B of node B (a redirector), towards port C of node D (a redirector), towards port B of node F. Since that isn't a redirector, the thread will make C point to B. The same is done for each neighbor port (in parallel), completing the parallel reduction.

Lazy evaluation

The lazy evaluation algorithm is very different from the strict one. It works by traversing the graph, exploring it to find redexes that are "visible" on the normal form of the term, skipping unnecessary branches. It is interesting because it allows avoiding wasting work; for example, ({a b}b)(f(42), 7) would quickly evaluate to 7, no matter how long f(42) takes to compute. In exchange, it is "less parallel" than the strict algorithm (we can't reduce all redexes since we don't know if they're necessary), and it requires global garbage collection (since erasure nodes are ignored).

To skip unnecessary branches, we must walk through the graph from port to port, using a strategy very similar to the denotational semantics of symmetric interaction combinators. First, we start walking from the root port to its target port. Then, until we get back to the root, do as follows:

  1. If we're walking from an aux port towards an aux port of a node, add the aux we're coming from to a stack, and move towards the main port of that node.

  2. If we're walking from a main port to an auxiliary port, then we just found a node that is part of the normal form of the graph! If we're performing a weak-head normal form reduction, stop. Otherwise, start walking towards each auxiliary port (either recursively, or in parallel).

  3. If we're walking towards root, halt.

This is a rough pseudocode:

def reduce_lazy(net, start):
  back = []
  prev = start
  next = net.enter(prev)

  while not(net.is_root(next)):
    if slot_of(prev) == 0 and slot_of(next) == 0:
      net.rewrite(prev, next)
    elif slot_of(next) == 0:
      for aux_n from 0 til net.aux_ports_of(next):
        net.reduce_lazy(Pointer(node_of(next), aux_n))
    else:
      back.push(prev)
      prev = Pointer(node_of(next), 0)
      next = net.enter(prev)

While the lazy algorithm is inherently sequential, there is still an opportunity to explore parallelism whenever we find a node that is part of the normal form of the graph (i.e., case 2). In that case, we can spawn a thread to walk towards each auxiliary port in parallel; i.e., the for-loop of the pseudocode can be executed in parallel like the one on the strict version. This would allow the algorithm to have many threads walking through the graph at the same time. Again, caution must be taken to avoid conflicts.

Trellis: a public event-log

Trellis is an append-only event-log divided into distinct labeled streams.

  • Trellis is backend agnostic and can have streams which run on a centralized server, a decentralized blockchain or any variation or permutation thereof.

  • Map(Word256, List(Word1024))

TODO

Forall: a global repository of knowledge

TODO: types are theorems, programs are proofs, files are papers, imports are citations. Forall is both a package manager and a substitute for academic publishing, where code can be used in mathematical publications, and proofs can be used in code.

Phos: a smart-contract platform

Phos is a Formality state-transition function, phos : Event -> PhosState -> PhosState, that interprets Trellis event stream as a cryptographic ledger and smart-contract platform.

Moonad

Moonad is a user-facing application that combines all the systems above in an unified package that just works. We call it an operating system in the sense it is capable of scheduling and running applications, but it isn't one in the traditional sense; as in, you won't be able to boot from it. It can be seen as a sandboxed application platform.

Moonad uses FM-Net as its low-level machine language, Formality as its user-facing language, Forall as its package-manager and Trellis as an abstraction of the internet and online interactions and Phos as a smart-contract platform. By combining those with a standard type for applications, App, Moonad is capable of renderizing interactive online applications that users send to Forall. Like many operating systems, it comes with a set of built-in, essential applications, including:

PhosWallet

Sending and receiving Phos Coins.

AppStore

Finding and publishing cool applications.

TrellisExplorer

Browsing the global event-log.

Provit

Placing code/proof bounties on types.

Forall

Uploading and downloading files to the package manager.

Formality-IDE

Editor, evaluator, debugger and type-checker for Formality, including interaction net visualization.

TODO

References

[2]: Yves Lafont, Interation Combinators, Institut de Mathematiques de Luminy, 1997 (https://pdfs.semanticscholar.org/6cfe/09aa6e5da6ce98077b7a048cb1badd78cc76.pdf)