分治算法,根据字面意思解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
分治策略:对于一个规模为 n 的问题,若该问题可以容易地解决(比如说规模 n 较小)则直接解决,否则将其分解为 k 个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。 在平时日常生活中,分治思想也是随处可见的。例如:当我们打牌时,在进行洗牌时,若牌的数目较多,一个人洗不过来,则会将牌进行分堆,单独洗一小堆牌是相对容易的,每一堆牌都洗完之后再放到一起,则完成洗牌过程。
- 该问题的规模缩小到一定的程度就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
分治法在每一层递归上都有三个步骤:
- 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题。
- 求解:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题。
- 合并:将各个子问题的解合并为原问题的解。
我们用有序度来表示一组数据的有序程度,用逆序度表示一组数据的无序程度。
假设我们有 n 个数据,我们期望数据从小到大排列,那完全有序的数据的有序度就是 n(n-1)/2,逆序度等于 0;相反,倒序排列的数据的有序度就是 0,逆序度是 n(n-1)/2。除了这两种极端情况外,我们通过计算有序对或者逆序对的个数,来表示数据的有序度或逆序度。
示例:
输入:[2, 4, 3, 1, 5, 6]
输出:4
// 逆序对:(2, 1) (4, 3) (4, 1) (3, 1)
我们套用分治的思想来求数组 A 的逆序对个数。我们可以将数组分成前后两半 A1 和 A2,分别计算 A1 和 A2 的逆序对个数 K1 和 K2,然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1+K2+K3。
使用分治算法其中一个要求是,子问题合并的代价不能太大,否则就起不了降低时间复杂度的效果了。那回到这个问题,如何快速计算出两个子问题 A1 与 A2 之间的逆序对个数呢?
这里就要借助归并排序算法了。你可以先试着想想,如何借助归并排序算法来解决呢?
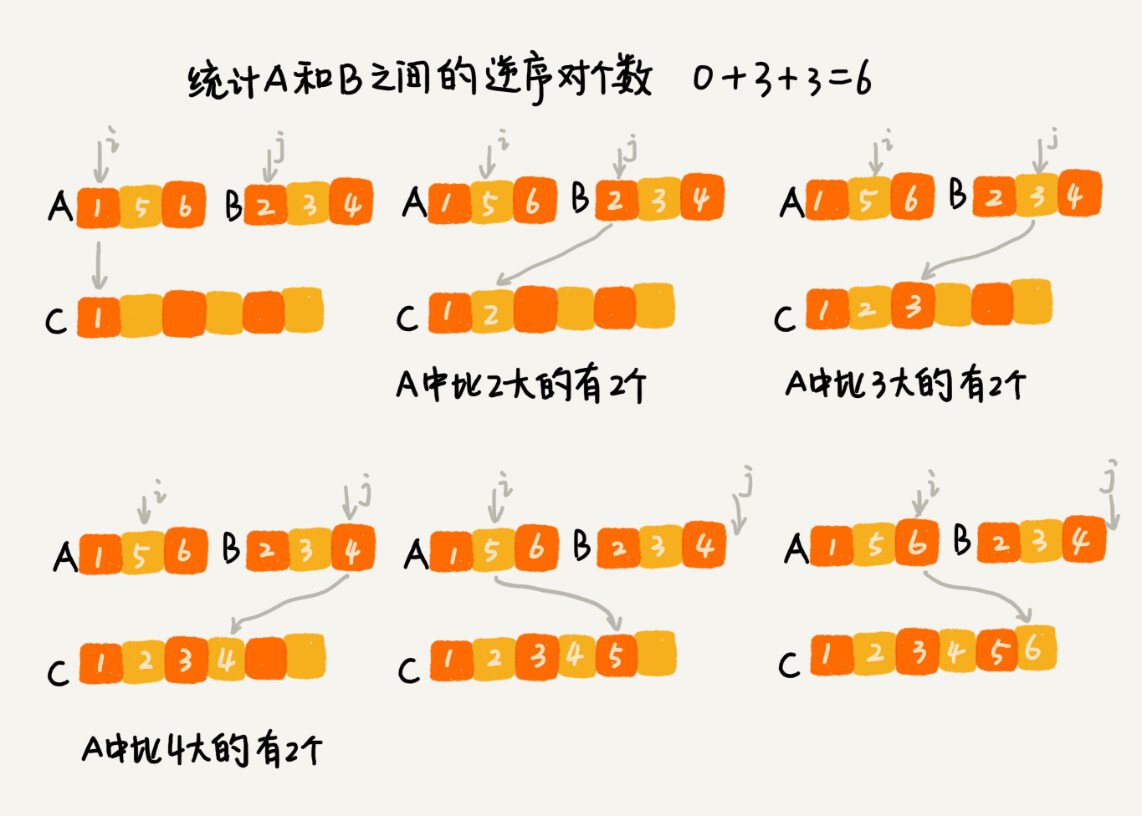
归并排序中有一个非常关键的操作,就是将两个有序的小数组,合并成一个有序的数组。实际上,在这个合并的过程中,我们就可以计算这两个小数组的逆序对个数了。每次合并操作,我们都计算逆序对个数,把这些计算出来的逆序对个数求和,就是这个数组的逆序对个数了。
// 计算逆序度
func countReverse(a []int) int {
// 递归终止条件
if len(a) <= 1 {
return 0
}
// 分解成两个子问题
pivot := len(a) / 2
left := countReverse(a[:pivot])
right := countReverse(a[pivot:])
// 最后进行合并
return left + right + merge(a, pivot)
}
func merge(a []int, pivot int) int {
left := a[:pivot]
right := a[pivot:]
count := 0 // 统计逆序对数
// tmp 用来临时存放合并后的结果
tmp := make([]int, 0, len(a))
i, j := 0, 0
for ; i < len(left) && j < len(right); {
if left[i] <= right[j] {
tmp = append(tmp, left[i])
i++
} else {
tmp = append(tmp, right[j])
count += len(left) - i
j++
}
}
// 处理剩下的部分
if i < len(left) {
tmp = append(tmp, left[i:]...)
} else if j < len(right) {
tmp = append(tmp, right[j:]...)
}
// 将最终结果复制回a
copy(a, tmp)
return count
}在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制: (1) 每次只能移动一个盘子; (2) 盘子只能从柱子顶端滑出移到下一根柱子; (3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
示例2:
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
- 如果只有 1 个盘子,则不需要利用 B 塔,直接将盘子从 A 移动到 C 。
- 如果有 2 个盘子,可以先将盘子 2 上的盘子 1 移动到 B ;将盘子 2 移动到 C ;将盘子 1 移动到 C 。这说明了:可以借助 B 将 2 个盘子从 A 移动到 C ,当然,也可以借助 C 将 2 个盘子从 A 移动到 B 。
- 如果有 3 个盘子,那么根据 2 个盘子的结论,可以借助 C 将盘子 3 上的两个盘子从 A 移动到 B ;将盘子 3 从 A 移动到 C ,A 变成空座;借助 A 座,将 B 上的两个盘子移动到 C 。
以此类推,上述思路可以一直扩展到 n 个盘子的情况:
1. 分解:
将求解移动 n 个盘子,分解为求解移动 n-1 个盘子,以借助 B 塔为例,可以借助空塔 B 将盘子 A 上面的 n-1 个盘子从 A 移动到 B;将 A 最大的盘子移动到 C,此时 A 变成了空塔;借助空塔 A,将 B 塔上的 n - 2 个盘子移动到 A,将 C 最大的盘子移动到 B,此时 B 成为空塔。
将 A,B,C塔进一步抽象为 from, mid, to ,通过一个移动盘子的方法 move,最终将 from 中的盘子借助一个空塔 mid 全部移动到 to ,该移动过程用 move(n, from, to, mid) ,其中 n 表示要移动的盘子数目。
2. 求解:
当子问题被分解到可以直接求解的时候,也就是当 n == 0 一个盘子也不需要移动,和 n == 1 时,我们不需要借助 mid 就可以直接移动到 to。
一般情况:
首先将 n-1 个盘子从 from 借助 to 移动到 mid。
move(n-1, from, to, mid) ,移动过后,mid 上拥有 n-1 个盘子,to 成为了空塔。
然后将 1 个盘子从 from 借助 mid 移动到 to。注意此处在之前其实解释了,在只有一个盘子的时候,直接从 from 移动到 to,不需要借助任何塔。
move(1, from, mid, to),移动过后,to 已经有了最大的盘子,from 变成了空塔。
最后将 n-1 个盘子从 mid 借助空塔 from 移动到 to。
move(n-1, mid, from, to),移动过后,mid 和 from 成为了空塔,to 则拥有了正确摆放的盘子。
3. 合并
递归求解其实就很自然的包含了这个合并的过程。
func hanota(A []int, B []int, C []int) []int {
if len(A) == 0 {
return nil
}
var move func(int, *[]int, *[]int, *[]int)
move = func(n int, from, mid, to *[]int) {
if n == 0 {
return
}
if n == 1 {
*to = append(*to, (*from)[len(*from) - 1])
*from = (*from)[:len(*from) - 1]
return
}
move(n-1, from, to, mid)
move(1, from, mid, to)
move(n-1, mid, from, to)
}
move(len(A), &A, &B, &C)
return C
}分治算法思想的应用是非常广泛的,并不仅限于指导编程和算法设计。它还经常用在海量数据处理的场景中。我们前面讲的数据结构和算法,大部分都是基于内存存储和单机处理。但是,如果要处理的数据量非常大,没法一次性放到内存中,这个时候,这些数据结构和算法就无法工作了。
比如,给 10GB 的订单文件按照金额排序这样一个需求,看似是一个简单的排序问题,但是因为数据量大,有 10GB,而我们的机器的内存可能只有 2、3GB 这样子,无法一次性加载到内存,也就无法通过单纯地使用快排、归并等基础算法来解决了。
要解决这种数据量大到内存装不下的问题,我们就可以利用分治的思想。我们可以将海量的数据集合根据某种方法,划分为几个小的数据集合,每个小的数据集合单独加载到内存来解决,然后再将小数据集合合并成大数据集合。实际上,利用这种分治的处理思路,不仅仅能克服内存的限制,还能利用多线程或者多机处理,加快处理的速度。
比如刚刚举的那个例子,给 10GB 的订单排序,我们就可以先扫描一遍订单,根据订单的金额,将 10GB 的文件划分为几个金额区间。比如订单金额为 1 到 100 元的放到一个小文件,101 到 200 之间的放到另一个文件,以此类推。这样每个小文件都可以单独加载到内存排序,最后将这些有序的小文件合并,就是最终有序的 10GB 订单数据了。
如果订单数据存储在类似 GFS 这样的分布式系统上,当 10GB 的订单被划分成多个小文件的时候,每个文件可以并行加载到多台机器上处理,最后再将结果合并在一起,这样并行处理的速度也加快了很多。不过,这里有一个点要注意,就是数据的存储与计算所在的机器是同一个或者在网络中靠的很近(比如一个局域网内,数据存取速度很快),否则就会因为数据访问的速度,导致整个处理过程不但不会变快,反而有可能变慢。
为什么说 MapReduce 的本质就是分治思想?我们刚刚举的订单的例子,数据有 10GB 大小,可能给你的感受还不强烈。那如果我们要处理的数据是 1T、10T、100T 这样子的,那一台机器处理的效率肯定是非常低的。而对于谷歌搜索引擎来说,网页爬取、清洗、分析、分词、计算权重、倒排索引等等各个环节中,都会面对如此海量的数据(比如网页)。所以,利用集群并行处理显然是大势所趋。
一台机器过于低效,那我们就把任务拆分到多台机器上来处理。如果拆分之后的小任务之间互不干扰,独立计算,最后再将结果合并。这不就是分治思想吗?
实际上,MapReduce 框架只是一个任务调度器,底层依赖 GFS 来存储数据,依赖 Borg 管理机器。它从 GFS 中拿数据,交给 Borg 中的机器执行,并且时刻监控机器执行的进度,一旦出现机器宕机、进度卡壳等,就重新从 Borg 中调度一台机器执行。
尽管 MapReduce 的模型非常简单,但是在 Google 内部应用非常广泛。它除了可以用来处理这种数据与数据之间存在关系的任务,比如 MapReduce 的经典例子,统计文件中单词出现的频率。除此之外,它还可以用来处理数据与数据之间没有关系的任务,比如对网页分析、分词等,每个网页可以独立的分析、分词,而这两个网页之间并没有关系。网页几十亿、上百亿,如果单机处理,效率低下,我们就可以利用 MapReduce 提供的高可靠、高性能、高容错的并行计算框架,并行地处理这几十亿、上百亿的网页。