动态规划需要掌握的预备知识:
用一句话解释动态规划就是**“记住你之前做过的事”,如果更准确些,其实是,“记住你之前得到的答案”**
我举个大家工作中经常遇到的例子。
在软件开发中,大家经常会遇到一些系统配置的问题,配置不对,系统就会报错,这个时候一般都会去 Google 或者是查阅相关的文档,花了一定的时间将配置修改好。
过了一段时间,去到另一个系统,遇到类似的问题,这个时候已经记不清之前修改过的配置文件长什么样,这个时候有两种方案,一种方案还是去 Google 或者查阅文档,另一种方案是借鉴之前修改过的配置,第一种做法其实是万金油,因为你遇到的任何问题其实都可以去 Google,去查阅相关文件找答案,但是这会花费一定的时间,相比之下,第二种方案肯定会更加地节约时间,但是这个方案是有条件的,条件如下:
- 之前的问题和当前的问题有着关联性,换句话说,之前问题得到的答案可以帮助解决当前问题
- 需要记录之前问题的答案
当然在这个例子中,可以看到的是,上面这两个条件均满足,大可去到之前配置过的文件中,将配置拷贝过来,然后做些细微的调整即可解决当前问题,节约了大量的时间。
不知道你是否从这些描述中发现,对于一个动态规划问题,我们只需要从两个方面考虑,那就是 找出问题之间的联系,以及 记录答案,这里的难点其实是找出问题之间的联系,记录答案只是顺带的事情,利用一些简单的数据结构就可以做到。
什么样的问题适合用动态规划来解决呢?换句话说,动态规划能解决的问题有什么规律可循呢?实际上,动态规划作为一个非常成熟的算法思想,很多人对此已经做了非常全面的总结。王争大神把这部分理论总结为“一个模型三个特征”。
什么是 “一个模型” ?它指的是动态规划适合解决的问题的模型。这个模型定义为 “多阶段决策最优解模型” 。
我们一般是用动态规划来解决最优问题。而解决问题的过程,需要经历多个决策阶段。每个决策阶段都对应着一组状态。然后我们寻找一组决策序列,经过这组决策序列,能够产生最终期望求解的最优值。
三个特征
1. 最优子结构
最优子结构指的是,问题的最优解包含子问题的最优解。反过来说就是,我们可以通过子问题的最优解,推导出问题的最优解。如果我们把最优子结构,对应到我们前面定义的动态规划问题模型上,那我们也可以理解为,后面阶段的状态可以通过前面阶段的状态推导出来。
2. 无后效性
无后效性有两层含义
- 第一层含义是,在推导后面阶段的状态的时候,我们只关心前面阶段的状态值,不关心这个状态是怎么一步一步推导出来的。
- 第二层含义是,某阶段状态一旦确定,就不受之后阶段的决策影响。
无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型,其实基本上都会满足无后效性。
3. 重复子问题
不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态。 (可以画递归树看出来)
我们先画出一个状态表。状态表一般都是二维的,所以你可以把它想象成二维数组。其中,每个状态包含三个变量,行、列、数组值。我们根据决策的先后过程,从前往后,根据递推关系,分阶段填充状态表中的每个状态。最后,我们将这个递推填表的过程,翻译成代码,就是动态规划代码了。
尽管大部分状态表都是二维的,但是如果问题的状态比较复杂,需要很多变量来表示,那对应的状态表可能就是高维的,比如三维、四维。那这个时候,我们就不适合用状态转移表法来解决了。一方面是因为高维状态转移表不好画图表示,另一方面是因为人脑确实很不擅长思考高维的东西。
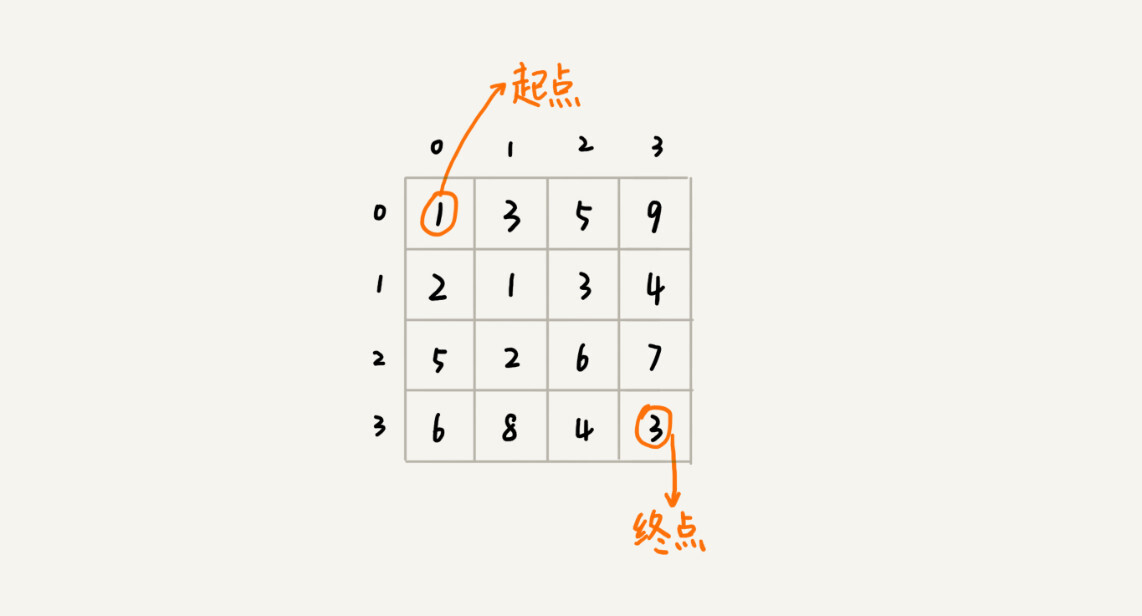
假设我们有一个 n 乘以 n 的矩阵 w[n][n] 。矩阵存储的都是正整数。棋子起始位置在左上角,终止位置在右下角。我们将棋子从左上角移动到右下角。每次只能向右或者向下移动一位。从左上角到右下角,会有很多不同的路径可以走。我们把每条路径经过的数字加起来看作路径的长度。那从左上角移动到右下角的最短路径长度是多少呢?
我们先看看,这个问题是否符合“一个模型”?
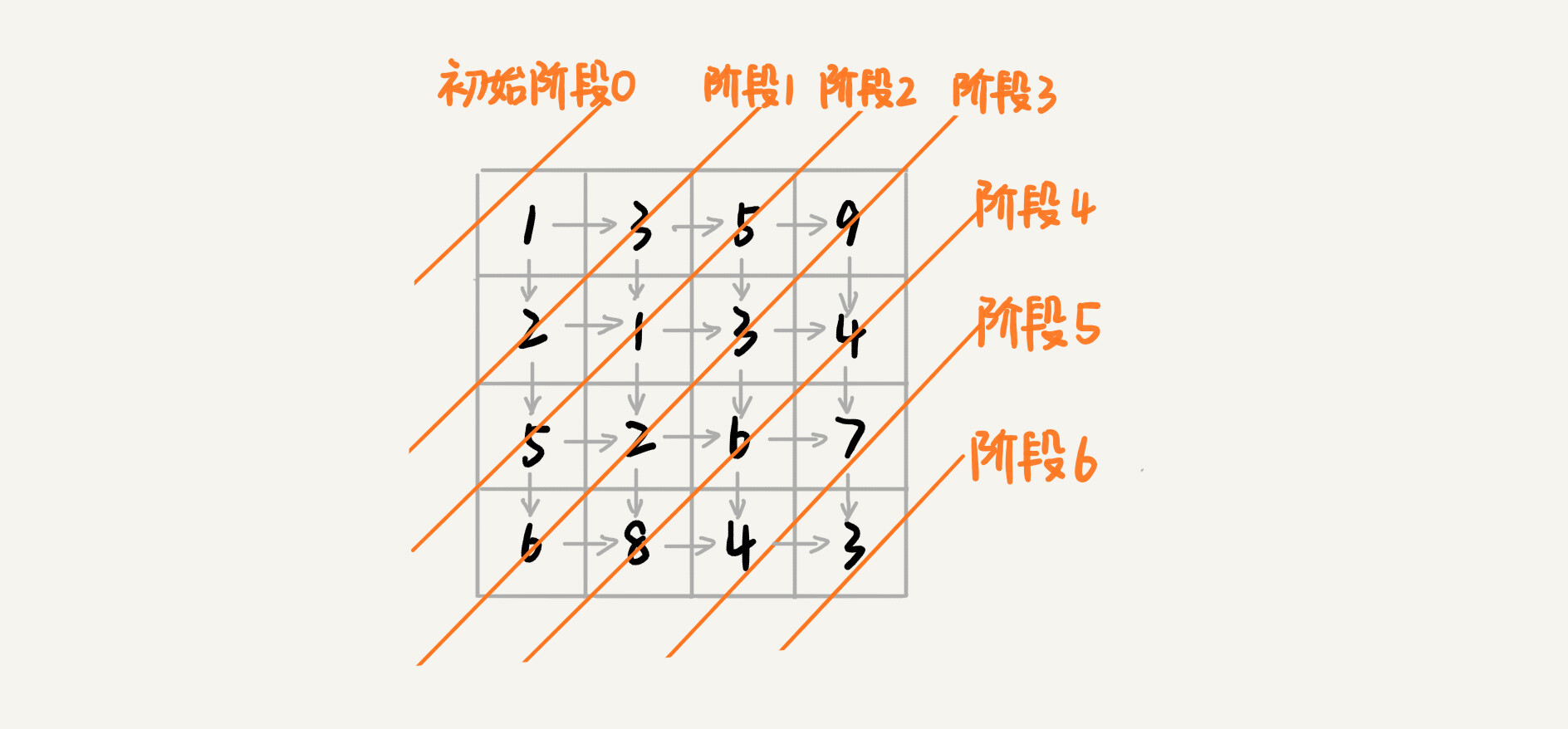
从 (0, 0) 走到 (n-1, n-1),总共要走 2*(n-1) 步,也就对应着 2*(n-1) 个阶段。每个阶段都有向右走或者向下走两种决策,并且每个阶段都会对应一个状态集合。
我们把状态定义为 min_dist(i, j),其中 i 表示行,j 表示列。min_dist 表达式的值表示从 (0, 0) 到达 (i, j) 的最短路径长度。所以,这个问题是一个多阶段决策最优解问题,符合动态规划的模型。
我们再来看,这个问题是否符合“三个特征”?
我们可以用回溯算法来解决这个问题。如果你自己写一下代码,画一下递归树,就会发现,递归树中有重复的节点。重复的节点表示,从左上角到节点对应的位置,有多种路线,这也能说明这个问题中存在重复子问题。
如果我们走到 (i, j) 这个位置,我们只能通过 (i-1, j),(i, j-1) 这两个位置移动过来,也就是说,我们想要计算 (i, j) 位置对应的状态,只需要关心 (i-1, j),(i, j-1) 两个位置对应的状态,并不关心棋子是通过什么样的路线到达这两个位置的。而且,我们仅仅允许往下和往右移动,不允许后退,所以,前面阶段的状态确定之后,不会被后面阶段的决策所改变,所以,这个问题符合“无后效性”这一特征。
刚刚定义状态的时候,我们把从起始位置 (0, 0) 到 (i, j) 的最小路径,记作 min_dist(i, j)。因为我们只能往右或往下移动,所以,我们只有可能从 (i, j-1) 或者 (i-1, j) 两个位置到达 (i, j)。也就是说,到达 (i, j) 的最短路径要么经过 (i, j-1),要么经过 (i-1, j),而且到达 (i, j) 的最短路径肯定包含到达这两个位置的最短路径之一。换句话说就是,min_dist(i, j) 可以通过 min_dist(i, j-1) 和 min_dist(i-1, j) 两个状态推导出来。这就说明,这个问题符合“最优子结构”。
min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))
现在,我们来看一下,如何套用这个状态转移表法,来解决之前那个矩阵最短路径的问题?
从起点到终点,我们有很多种不同的走法。我们可以穷举所有走法,然后对比找出一个最短走法。不过如何才能无重复又不遗漏地穷举出所有走法呢?我们可以用回溯算法这个比较有规律的穷举算法。
回溯算法的代码实现如下所示:
func main() {
board := [][]int{
{1, 3, 5, 9},
{2, 1, 3, 4},
{5, 2, 6, 7},
{6, 8, 4, 3},
}
/*
{1, 4, 9, 18},
{3, 4, 7, 11},
{8, 6, 12,18},
{14,14,16,19},
*/
fmt.Println(minDistance(board, 4)) // 19
}
// n*n的网格board
func minDistance(board [][]int, n int) int {
backtrack(0, 0, board[0][0], board, n)
return minDist
}
var minDist = math.MaxInt64
func backtrack(i, j, dist int, board [][]int, n int) {
if i == n - 1 && j == n - 1 {
if dist < minDist {
minDist = dist
}
return
}
if i + 1 < n { // 往下走
backtrack(i+1, j, dist + board[i+1][j], board, n)
}
if j + 1 < n { // 往右走
backtrack(i, j+1, dist + board[i][j+1], board, n)
}
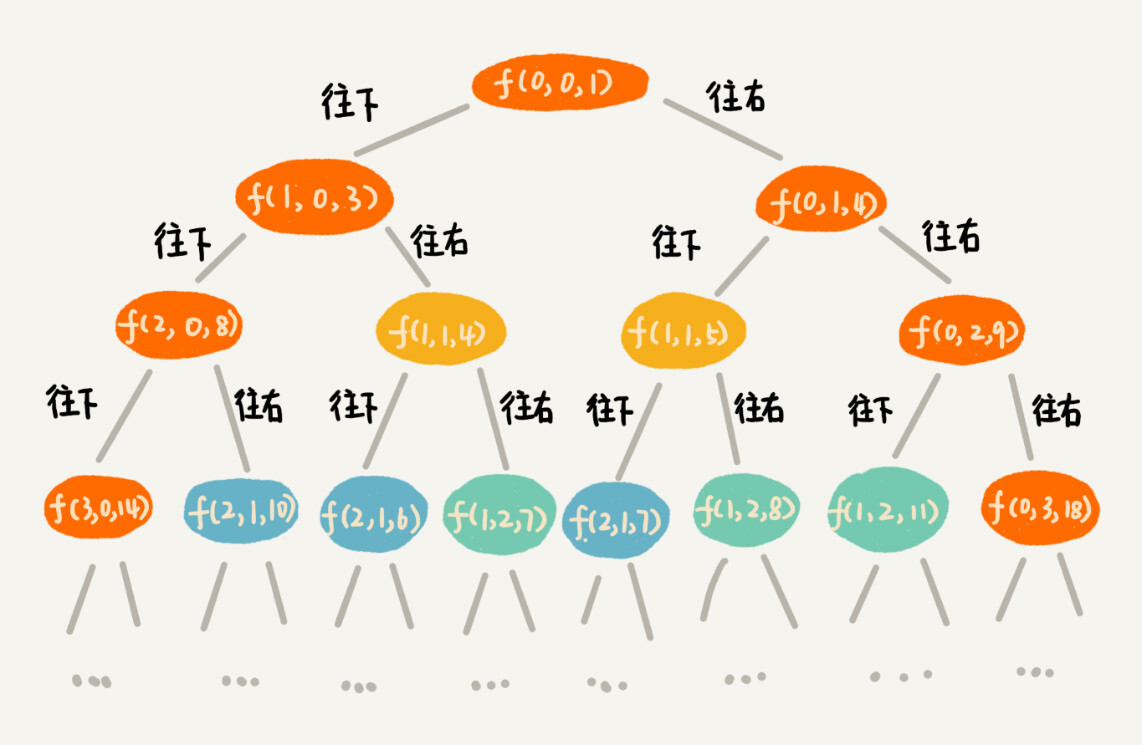
}有了回溯代码之后,接下来,我们要画出递归树,以此来寻找重复子问题。在递归树中,一个状态(也就是一个节点)包含三个变量 (i, j, dist),其中 i,j 分别表示行和列,dist 表示从起点到达 (i, j) 的路径长度。从图中,我们看出,尽管 (i, j, dist) 不存在重复的,但是 (i, j) 重复的有很多。对于 (i, j) 重复的节点,我们只需要选择 dist 最小的节点,继续递归求解,其他节点就可以舍弃了。
既然存在重复子问题,我们就可以尝试看下,是否可以用动态规划来解决呢?
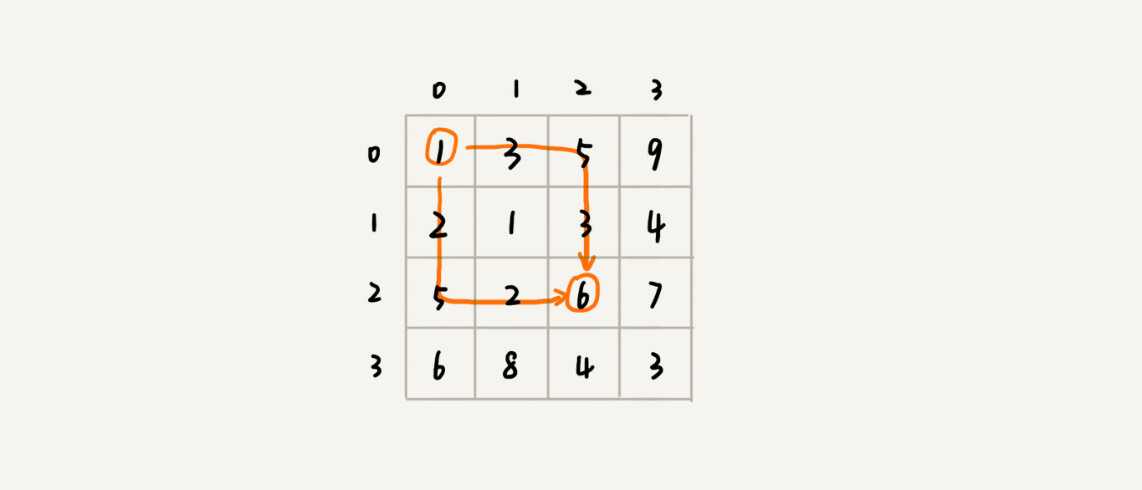
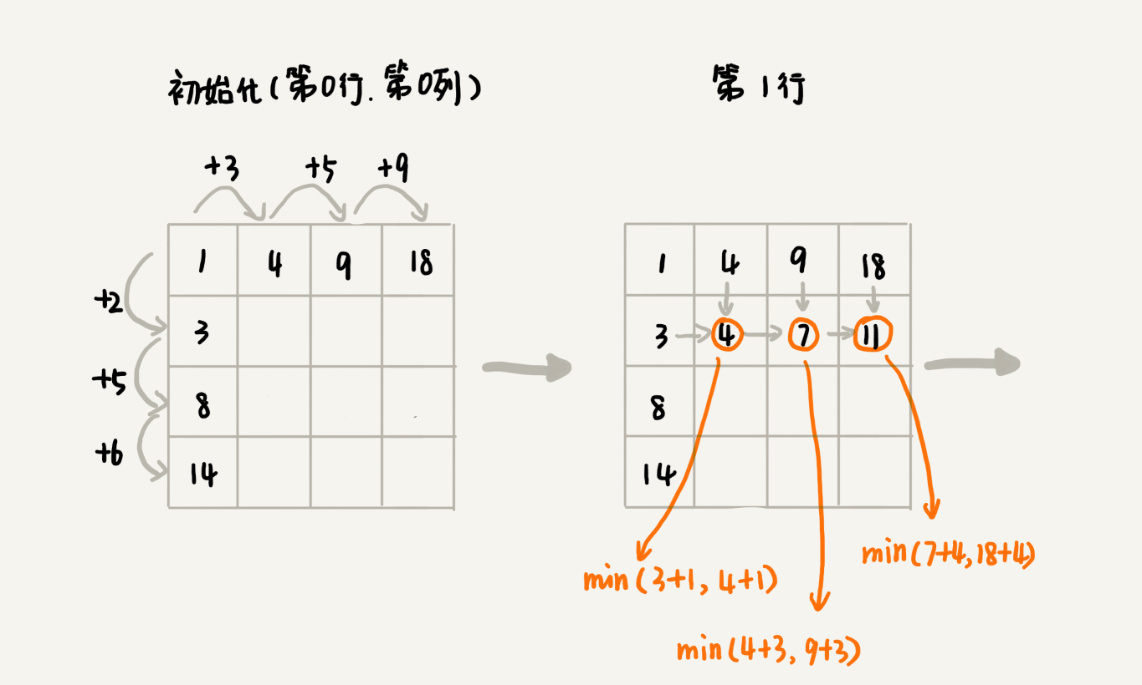
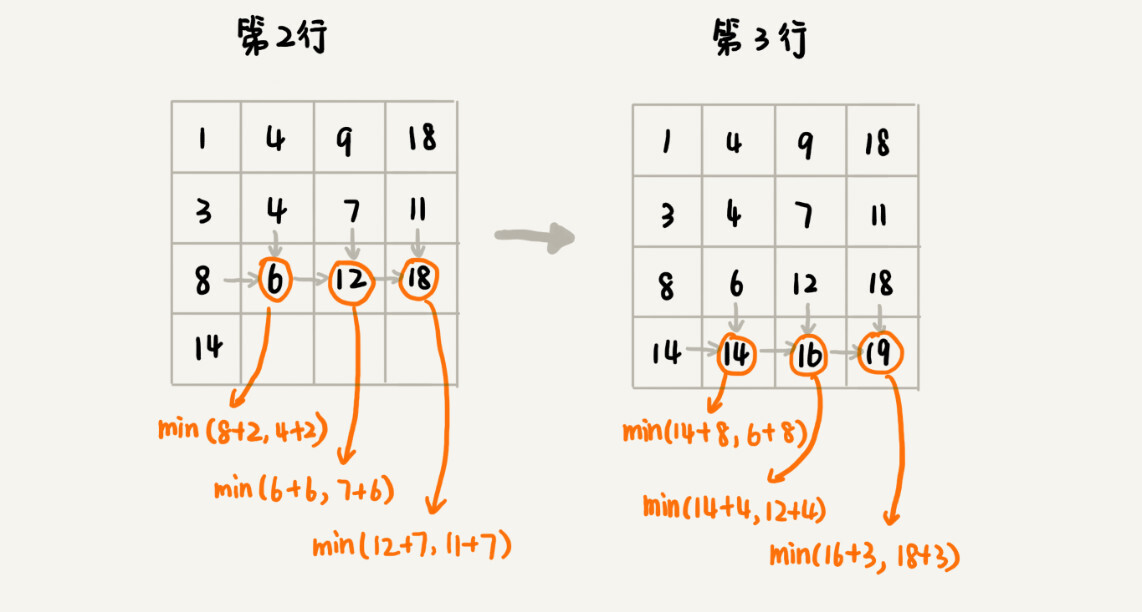
我们画出一个二维状态表,表中的行、列表示棋子所在的位置,表中的数值表示从起点到这个位置的最短路径。我们按照决策过程,通过不断状态递推演进,将状态表填好。为了方便代码实现,我们按行来进行依次填充。
弄懂了填表的过程,代码实现就简单多了。我们将上面的过程,翻译成代码,就是下面这个样子。结合着代码、图和文字描述,应该更容易理解我讲的内容。
// n*n的网格board
func minDistance(board [][]int, n int) int {
states := make([][]int, n)
for i := range states {
states[i] = append(states[i], make([]int, n)...)
}
states[0][0] = board[0][0]
for j := 1; j < n; j++ { // 初始化第一行
states[0][j] = states[0][j-1] + board[0][j]
}
for i := 1; i < n; i++ { // 初始化第一列
states[i][0] = states[i-1][0] + board[i][0]
}
for i := 1; i < n; i++ {
for j := 1; j < n; j++ {
// 这一步其实就是状态转移方程的代码实现
states[i][j] = min(states[i-1][j], states[i][j-1]) + board[i][j]
}
}
return states[n-1][n-1]
}
func min(x, y int) int {
if x <= y {
return x
}
return y
}思考一下,还能不能更简化?现在空间复杂度由于用了一个二维数组,是比较高的,可以换成一维数组吗?我在下面给出了实现,你先尝试不看,自己能不能做出来。
// n*n的网格board
func minDistance(board [][]int, n int) int {
states := make([]int, n)
states[0] = board[0][0]
for i := 1; i < n; i++ { // 初始化第一行数据
states[i] = states[i-1] + board[0][i]
}
for i := 1; i < n; i++ { // 推导接下来的第 i 行数据
for j := 0; j < n; j++ {
left := math.MaxInt64
if j - 1 >= 0 {
left = states[j-1]
}
up := states[j]
// 递推方程
states[j] = min(left, up) + board[i][j]
}
}
return states[n-1]
}由于递推 dp[i][j] 的状态,只需要知道 dp[i-1][j] 和 dp[i][j-1] 。把图中的二维数组的每一行独立开,当成一个一维数组,可以发现在计算 dp[i][j] 的时候,上一行的数据 dp[i-1][j] 还没有被覆盖,因此转换成一维数组是完全可以行的。
一般解决动态规划问题,分为四个步骤,分别是
- 问题拆解,找到问题之间的具体联系
- 状态定义
- 递推方程推导
- 实现
这里面的重点其实是前两个,如果前两个步骤顺利完成,后面的递推方程推导和代码实现会变得非常简单。
这里还是拿 Quora 上面的例子来讲解,“1+1+1+1+1+1+1+1” 得出答案是 8,那么如何快速计算 “1+ 1+1+1+1+1+1+1+1”,我们首先可以对这个大的问题进行拆解,这里我说的大问题是 9 个 1 相加,这个问题可以拆解成 1 + “8 个 1 相加的答案”,8 个 1 相加继续拆,可以拆解成 1 + “7 个 1 相加的答案”,… 1 + “0 个 1 相加的答案”,到这里,第一个步骤 已经完成。
状态定义 其实是需要思考在解决一个问题的时候我们做了什么事情,然后得出了什么样的答案,对于这个问题,当前问题的答案就是当前的状态,基于上面的问题拆解,你可以发现两个相邻的问题的联系其实是 后一个问题的答案 = 前一个问题的答案 + 1,这里,状态的每次变化就是 +1。
定义好了状态,递推方程就变得非常简单,就是 dp[i] = dp[i - 1] + 1,这里的 dp[i] 记录的是当前问题的答案,也就是当前的状态,dp[i - 1] 记录的是之前相邻的问题的答案,也就是之前的状态,它们之间通过 +1 来实现状态的变更。
最后一步就是实现了,有了状态表示和递推方程,实现这一步上需要重点考虑的其实是初始化,就是用什么样的数据结构,根据问题的要求需要做那些初始值的设定。
public int dpExample(int n) {
int[] dp = new int[n + 1]; // 多开一位用来存放 0 个 1 相加的结果
dp[0] = 0; // 0 个 1 相加等于 0
for (int i = 1; i <= n; ++i) {
dp[i] = dp[i - 1] + 1;
}
return dp[n];
}你可以看到,动态规划这四个步骤其实是相互递进的,状态的定义离不开问题的拆解,递推方程的推导离不开状态的定义,最后的实现代码的核心其实就是递推方程,这中间如果有一个步骤卡壳了则会导致问题无法解决,当问题的复杂程度增加的时候,这里面的思维复杂程度会上升。
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例1:
输入:2
输出:2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例2:
输入:3
输出:3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
爬楼梯,可以爬一步也可以爬两步,问有多少种不同的方式到达终点,我们按照上面提到的四个步骤进行分析:
-
问题拆解:
我们到达第 n 个楼梯可以从第 n – 1 个楼梯和第 n – 2 个楼梯到达,因此第 n 个问题可以拆解成第 n – 1 个问题和第 n – 2 个问题,第 n – 1 个问题和第 n – 2 个问题又可以继续往下拆,直到第 0 个问题,也就是第 0 个楼梯 (起点)
-
状态定义
“问题拆解” 中已经提到了,第 n 个楼梯会和第 n – 1 和第 n – 2 个楼梯有关联,那么具体的联系是什么呢?你可以这样思考,第 n – 1 个问题里面的答案其实是从起点到达第 n – 1 个楼梯的路径总数,n – 2 同理,从第 n – 1 个楼梯可以到达第 n 个楼梯,从第 n – 2 也可以,并且路径没有重复,因此我们可以把第 i 个状态定义为 “从起点到达第 i 个楼梯的路径总数”,状态之间的联系其实是相加的关系。
-
递推方程
“状态定义” 中我们已经定义好了状态,也知道第 i 个状态可以由第 i – 1 个状态和第 i – 2 个状态通过相加得到,因此递推方程就出来了
dp[i] = dp[i - 1] + dp[i - 2] -
实现
你其实可以从递推方程看到,我们需要有一个初始值来方便我们计算,起始位置不需要移动
dp[0] = 0,第 1 层楼梯只能从起始位置到达,因此dp[1] = 1,第 2 层楼梯可以从起始位置和第 1 层楼梯到达,因此dp[2] = 2,有了这些初始值,后面就可以通过这几个初始值进行递推得到。
Java
public int climbStairs(int n) {
if (n == 1) {
return 1;
}
int[] dp = new int[n + 1]; // 多开一位,考虑起始位置
dp[0] = 0; dp[1] = 1; dp[2] = 2;
for (int i = 3; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}Go
func climbStairs(n int) int {
// 状态定义:对于爬n个台阶,最后一次爬1个台阶的爬法为f(n-1),最后一次爬2个台阶的爬法为f(n-2)
// 递推公式:
// f(n) = 1 (n <= 1时)
// f(n) = f(n-1) + f(n-2) (n >= 2)
if n <= 1 {
return 1
}
dp := make([]int, n+1)
dp[0], dp[1] = 1, 1
for i := 2; i <= n; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
给定一个三角形数组,需要求出从上到下的最小路径和,也和之前一样,按照四个步骤来分析:
-
问题拆解:
这里的总问题是求出最小的路径和,路径是这里的分析重点,路径是由一个个元素组成的,和之前爬楼梯那道题目类似,
[i][j]位置的元素,经过这个元素的路径肯定也会经过[i - 1][j]或者[i - 1][j - 1],因此经过一个元素的路径和可以通过这个元素上面的一个或者两个元素的路径和得到。 -
状态定义
状态的定义一般会和问题需要求解的答案联系在一起,这里其实有两种方式,一种是考虑路径从上到下,另外一种是考虑路径从下到上,因为元素的值是不变的,所以路径的方向不同也不会影响最后求得的路径和,如果是从上到下,你会发现,在考虑下面元素的时候,起始元素的路径只会从
[i - 1][j]获得,每行当中的最后一个元素的路径只会从[i - 1][j - 1]获得,中间二者都可,这样不太好实现,因此这里考虑从下到上的方式,状态的定义就变成了 “最后一行元素到当前元素的最小路径和”,对于[0][0]这个元素来说,最后状态表示的就是我们的最终答案。 -
递推方程
“状态定义” 中我们已经定义好了状态,递推方程就出来了
dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle[i][j] -
实现
这里初始化时,我们需要将最后一行的元素填入状态数组中,然后就是按照前面分析的策略,从下到上计算即可
Java
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[][] dp = new int[n][n];
List<Integer> lastRow = triangle.get(n - 1);
for (int i = 0; i < n; ++i) {
dp[n - 1][i] = lastRow.get(i);
}
for (int i = n - 2; i >= 0; --i) {
List<Integer> row = triangle.get(i);
for (int j = 0; j < i + 1; ++j) {
dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + row.get(j);
}
}
return dp[0][0];
}Go
func minimumTotal(triangle [][]int) int {
// 状态定义:某结点[i][j]的最小路径和为左右结点[i+1][j] 或 [i+1][j+1] 的最小路径和 加上本结点值
// 最终结点[0][0]的值即为所求结果
// 递推公式:
// f(i, j) = triangle[i][j] (i == len(triangle))
// f(i, j) = triangle[i][j] + min(f(i+1, j), f(i+1, j+1))
for i := len(triangle) - 2; i >= 0; i-- {
for j := 0; j < i+1; j++ {
min := int(math.Min(float64(triangle[i+1][j]), float64(triangle[i+1][j+1])))
triangle[i][j] = triangle[i][j] + min
}
}
return triangle[0][0]
}给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],输出: 6解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
求最大子数组和,非常经典的一道题目,这道题目有很多种不同的做法,而且很多算法思想都可以在这道题目上面体现出来,比如动态规划、贪心、分治,还有一些技巧性的东西,比如前缀和数组,这里还是使用动态规划的思想来解题,套路还是之前的四步骤:
-
问题拆解:
问题的核心是子数组,子数组可以看作是一段区间,因此可以由起始点和终止点确定一个子数组,两个点中,我们先确定一个点,然后去找另一个点,比如说,如果我们确定一个子数组的截止元素在 i 这个位置,这个时候我们需要思考的问题是 “以 i 结尾的所有子数组中,和最大的是多少?”,然后我们去试着拆解,这里其实只有两种情况:
i 这个位置的元素自成一个子数组;
i 位置的元素的值 + 以 i – 1 结尾的所有子数组中的子数组和最大的值
你可以看到,我们把第 i 个问题拆成了第 i – 1 个问题,之间的联系也变得清晰
-
状态定义
通过上面的分析,其实状态已经有了,
dp[i]就是 “以 i 结尾的所有子数组的最大值” -
递推方程
拆解问题的时候也提到了,有两种情况,即当前元素自成一个子数组,另外可以考虑前一个状态的答案,于是就有了
dp[i] = Math.max(dp[i - 1] + array[i], array[i])化简一下就成了:
dp[i] = Math.max(dp[i - 1], 0) + array[i] -
实现
题目要求子数组不能为空,因此一开始需要初始化,也就是
dp[0] = array[0],保证最后答案的可靠性,另外我们需要用一个变量记录最后的答案,因为子数组有可能以数组中任意一个元素结尾
Java
public int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int n = nums.length;
int[] dp = new int[n];
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < n; ++i) {
dp[i] = Math.max(dp[i - 1], 0) + nums[i];
result = Math.max(result, dp[i]);
}
return result;
}Go
func maxSubArray(nums []int) int {
// 状态定义:以i结尾的所有子数组的最大和是dp[i]
// 注意:dp[len(nums)-1]并非答案,因为最大连续子数组不一定是以下标len(nums)-1为结尾
mathematics
if len(nums) == 0 {
return 0
}
dp := make([]int, len(nums))
dp[0] = nums[0]
// 注意:result初始值并不是0
var result = dp[0]
for i := 1; i < len(nums); i++ {
max := int(math.Max(float64(dp[i-1]), 0))
dp[i] = max + nums[i]
result = int(math.Max(float64(dp[i]), float64(result)))
}
return result
}一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3
输出: 28
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 10 ^ 9
给定一个矩阵,问有多少种不同的方式从起点(0,0) 到终点 (m-1,n-1),并且每次移动只能向右或者向下,我们还是按之前提到的分析动态规划那四个步骤来思考一下:
-
问题拆解
题目中说了,每次移动只能是向右或者是向下,矩阵类动态规划需要关注当前位置和其相邻位置的关系,对于某一个位置来说,经过它的路径只能从它上面过来,或者从它左边过来,因此,如果需要求到达当前位置的不同路径,我们需要知道到达其上方位置的不同路径,以及到达其左方位置的不同路径
-
状态定义
矩阵类动态规划的状态定义相对来说比较简单,只需要看当前位置即可,问题拆解中,我们分析了当前位置和其邻居的关系,提到每个位置其实都可以算做是终点,状态表示就是 “从起点到达该位置的不同路径数目”
-
递推方程
有了状态,也知道了问题之间的联系,其实递推方程也出来了,就是
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
func uniquePaths(m int, n int) int {
dp := make([][]int, n)
for i := range dp {
for j := 0; j < m; j++ {
if i == 0 {
dp[0] = append(dp[0], 1)
continue
}
if j == 0 {
dp[i] = append(dp[i], 1)
continue
}
dp[i] = append(dp[i], dp[i-1][j]+dp[i][j-1])
}
}
return dp[n-1][m-1]
}一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
说明:m 和 n 的值均不超过 100。
示例 1:
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
在上面那道题的基础上,矩阵中增加了障碍物,这里只需要针对障碍物进行判断即可,如果当前位置是障碍物的话,状态数组中当前位置记录的答案就是 0,也就是没有任何一条路径可以到达当前位置,除了这一点外,其余的分析方法和解题思路和之前 一样 。
func uniquePathsWithObstacles(obstacleGrid [][]int) int {
if len(obstacleGrid) == 0 || len(obstacleGrid[0]) == 0 || obstacleGrid[0][0] == 1 {
return 0
}
row, col := len(obstacleGrid), len(obstacleGrid[0])
dp := make([][]int, row)
for i := range dp {
dp[i] = make([]int, col)
}
dp[0][0] = 1
for i := 1; i < row; i++ {
if obstacleGrid[i][0] == 1 {
dp[i][0] = 0
} else {
dp[i][0] = dp[i-1][0]
}
}
for j := 1; j < col; j++ {
if obstacleGrid[0][j] == 1 {
dp[0][j] = 0
} else {
dp[0][j] = dp[0][j-1]
}
}
for i := 1; i < row; i++ {
for j := 1; j < col; j++ {
if obstacleGrid[i][j] == 1 {
dp[i][j] = 0
continue
}
dp[i][j] = dp[i-1][j] + dp[i][j-1]
}
}
return dp[row-1][col-1]
}给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
给定一个矩阵,问从起点(0,0) 到终点 (m-1,n-1) 的最小路径和是多少,并且每次移动只能向右或者向下,按之四个步骤来思考一下:
-
问题拆解
拆解问题的方式方法和前两道题目非常类似,这里不同的地方只是记录的答案不同,也就是状态不同,我们还是可以仅仅考虑当前位置,然后可以看到只有上面的位置和左边的位置可以到达当前位置,因此当前问题就可以拆解成两个子问题
-
状态定义
因为是要求路径和,因此状态需要记录的是 “从起始点到当前位置的最小路径和”
-
递推方程
有了状态,以及问题之间的联系,我们知道了,当前的最短路径和可以由其上方和其左方的最短路径和对比得出,递推方程也可以很快写出来:
$$ dp(i, j) = min(dp(i - 1, j) + dp(i)(j - 1)) + grid(i, j) $$
func minPathSum(grid [][]int) int {
if len(grid) == 0 || len(grid[0]) == 0 {
return -1
}
for j := 1; j < len(grid[0]); j++ {
grid[0][j] = grid[0][j-1] + grid[0][j]
}
for i := 1; i < len(grid); i++ {
grid[i][0] = grid[i-1][0] + grid[i][0]
}
for i := 1; i < len(grid); i++ {
for j := 1; j < len(grid[0]); j++ {
min := int(math.Min(float64(grid[i-1][j]), float64(grid[i][j-1])))
grid[i][j] = grid[i][j] + min
}
}
return grid[len(grid)-1][len(grid[0])-1]
}在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积。
示例:
输入:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
输出: 4
引用自:LeetCode
可以使用动态规划降低时间复杂度。我们用 dp(i, j) 表示以 (i, j) 为右下角,且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i, j) 的值,那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值,其平方即为最大正方形的面积。
那么如何计算 dp 中的每个元素值呢?对于每个位置 (i, j),检查在矩阵中该位置的值:
如果该位置的值是 0,则 dp(i, j) = 0,因为当前位置不可能在由 1 组成的正方形中;
如果该位置的值是 1,则 dp(i, j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 1,状态转移方程如下:
$$ dp(i, j) = min(dp(i-1, j), dp(i-1, j-1), dp(i, j-1)) + 1 $$ 如果读者对这个状态转移方程感到不解, 可以参考 1277. 统计全为 1 的正方形子矩阵的官方题解,其中给出了详细的证明。
此外,还需要考虑边界条件。如果 ii 和 jj 中至少有一个为 00,则以位置 (i, j)(i,j) 为右下角的最大正方形的边长只能是 11,因此 dp(i, j) = 1dp(i,j)=1。
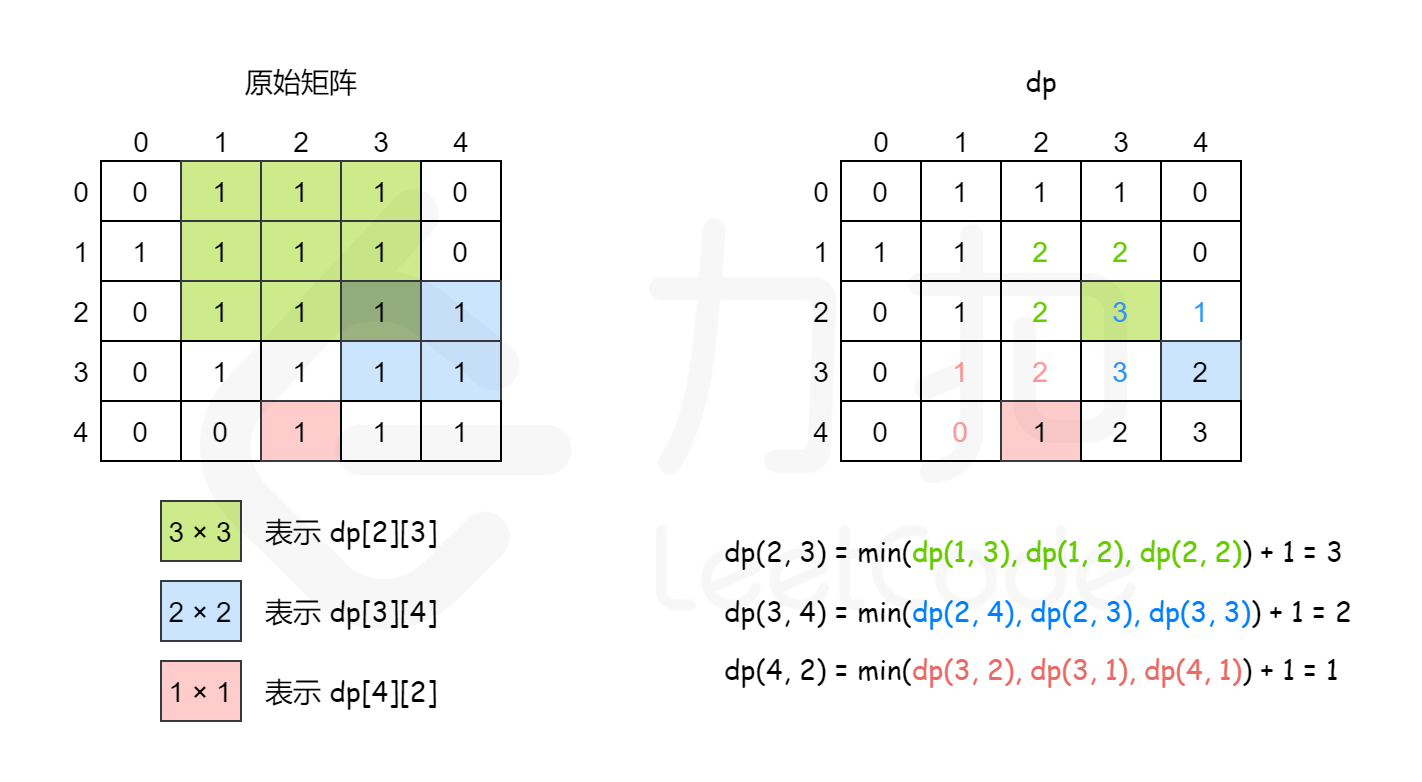
以下用一个例子具体说明。原始矩阵如下。
0 1 1 1 0
1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1
对应的 dpdp 值如下。
0 1 1 1 0
1 1 2 2 0
0 1 2 3 1
0 1 2 3 2
0 0 1 2 3
下图也给出了计算 dpdp 值的过程。
func maximalSquare(matrix [][]byte) int {
res := 0
m := len(matrix)
if m == 0 {return 0}
n := len(matrix[0])
var dp = make([][]int, m)
for i := 0; i < m; i++ {
dp[i] = make([]int, n)
for j := 0; j < n; j++ {
if i == 0 || j == 0 {
dp[i][j] = int(matrix[i][j] - '0')
} else if matrix[i][j] == '1' {
dp[i][j] = 1 + min(dp[i-1][j-1] , min(dp[i-1][j], dp[i][j-1]))
}
if dp[i][j] > res {
res = dp[i][j]
}
}
}
return res * res
}
func min(a, b int) int {
if a <= b {return a}
return b
}对于一组不同重量、不可分割的物品,我们需要选择一些装入背包,在满足背包最大重量限制的前提下,背包中物品总重量的最大值是多少呢?
示例:
输入:[2,2,4,6,3] 9
输出:9
-
问题拆解:
对于每一个物品,我们用其下标
i来表示,当轮到选择i物品是否装入背包的时候,我们假设i - 1的物品已经决定好了是否要装入背包。因此i - 1就可以推导出i的选择后的所有情况。以此类推,一直到0物品的情况。 -
状态定义
“问题拆解” 中已经提到了,第
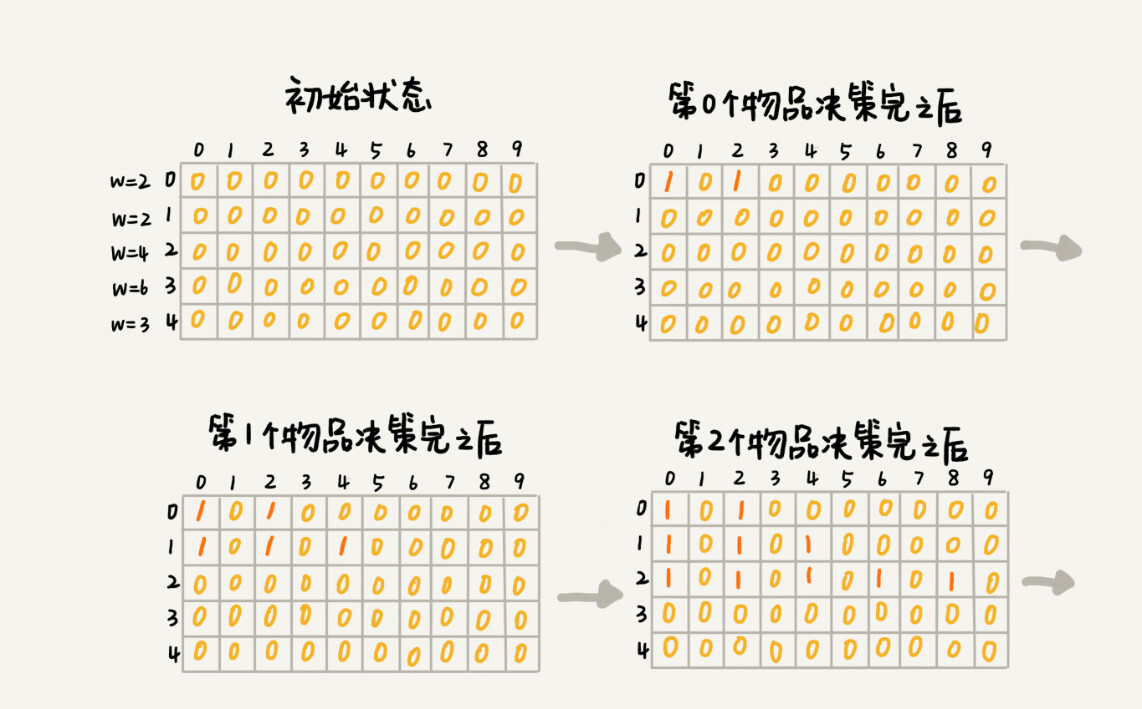
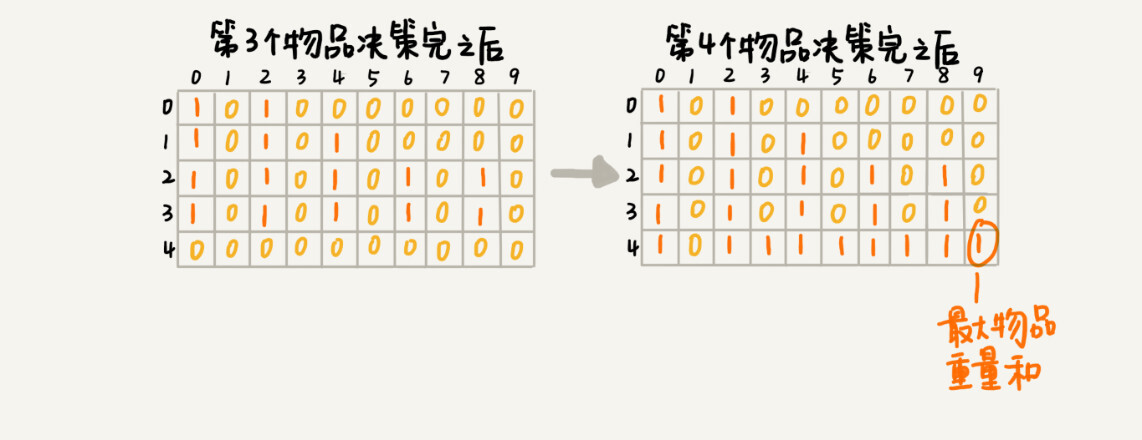
i个物品的选择会和第i – 1有关联,那么具体的联系是什么呢?你可以这样思考,第i - 1个物品的选择会得到经过本次选择后背包中所有可能的重量,那么第i个物品的选择,就是基于i - 1的基础上,考虑要不要选择i。如果不选择,那么之前i - 1选择后的所有可能不会发生改变。如果选择,那么需要在i - 1的所有可能的基础上加上i物品的重量。以示例为例:物品为
[2,2,4,6,3],那么在i == 0的时候,如果不选择,那么背包重量为0,如果选择,那么背包重量为2。在i == 1的时候,我们基于i == 0的结果,如果不选择,那么背包重量可能为0(0+0),2(2+0)。如果选择,那么背包重量可能为2(0+2),4(2+2)。那么所有可能的结果就是0,2,4。以此类推,我们就可以得到当i == n时的所有可能的结果,从这个结果里面选取最接近背包最大承重即可。可以用二维数组来存储这样一个状态,行为物品下标,列为可能的重量,其中存储的值0表示false,值1表示true,如图所示:
func knapsack(items []int, w int) int {
// 选择的结果记录
states := make([][]bool, len(items))
for i := 0; i < len(items); i++ {
states[i] = append(states[i], make([]bool, w+1)...)
}
// 处理第一行数据
states[0][0] = true
if items[0] <= w {
states[0][items[0]] = true
}
for i := 1; i < len(items); i++ {
// 不选 i 的情况
for j := 0; j < w+1; j++ {
if states[i-1][j] {
states[i][j] = true
}
}
// 把 i 放入背包的情况
for j := 0; j <= w - items[i]; j++ {
if states[i-1][j] {
states[i][j + items[i]] = true
}
}
}
for i := w; i >= 0; i-- { // 输出结果
if states[len(items)-1][i] {
return i
}
}
return 0
}如果你仔细观察,会发现 i 的状态跟 i - 1 的状态会有很大一部分的重叠,因此可以用一维数组来优化空间复杂度:
func knapsack(items []int, w int) int {
// 选择的结果记录
states := make([]bool, w+1)
// 处理第一行数据
states[0] = true
if items[0] <= w {
states[items[0]] = true
}
for i := 1; i < len(items); i++ {
// 把第 i 个物品放入背包
for j := w - items[i]; j >= 0; j-- {
if states[j] {
states[j + items[i]] = true
}
}
}
for i := w; i >= 0; i-- {
if states[i] {
return i
}
}
return 0
}淘宝的“双十一”购物节有各种促销活动,比如“满 200 元减 50 元”。假设你女朋友的购物车中有 n 个(n>100)想买的商品,她希望从里面选几个,在凑够满减条件的前提下,让选出来的商品价格总和最大程度地接近满减条件(200 元),这样就可以极大限度地“薅羊毛”。作为程序员的你,能不能编个代码来帮她搞定呢?
func main() {
items := []int{100, 20, 31, 87, 64, 19}
res := double11advance(items, 200)
sum := 0
for _, i := range res {
sum += items[i]
}
fmt.Printf("Buy: %v totalPrice: %d\n", res, sum)
// Output:
// Buy: [5 4 3 2] totalPrice: 201
}
// items 商品价格,w 满减条件
func double11advance(items []int, w int) []int {
var res []int
states := make([][]bool, len(items))
for i := 0; i < len(items); i++ {
states[i] = append(states[i], make([]bool, 3*w+1)...)
}
states[0][0] = true
if items[0] <= 3*w {
states[0][items[0]] = true
}
for i := 1; i < len(items); i++ {
// 不选择 i 的时候
for j := 0; j <= 3*w; j++ {
if states[i-1][j] {
states[i][j] = true
}
}
// 选择 i 的时候
for j := 0; j <= 3*w - items[i]; j++ {
if states[i-1][j] {
states[i][j + items[i]] = true
}
}
}
j := w
for ; j <= 3*w; j++ {
if states[len(items)-1][j] {
break
}
}
if j == 3*w+1 {
return nil // 没有可行解
}
for i := len(items) - 1; i >= 1; i-- {
if j - items[i] >= 0 && states[i-1][j - items[i]] {
res = append(res, i) // 购买该商品
j = j-items[i]
} // else 不需要购买该商品
}
if j != 0 { res = append(res, 0) }
return res
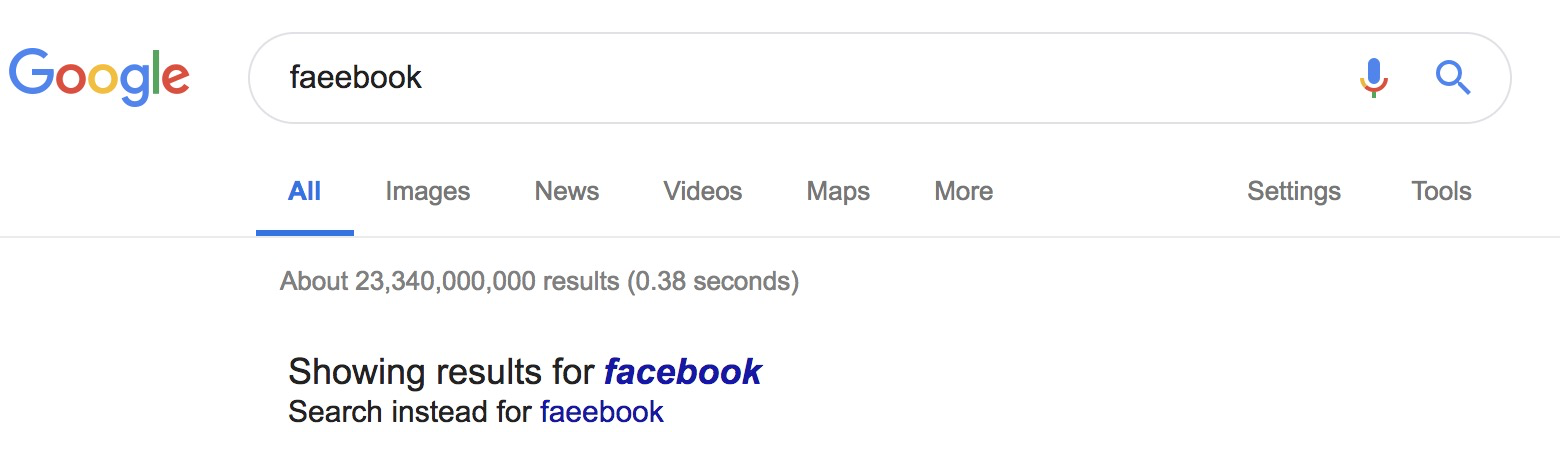
}当你在搜索框中,一不小心输错单词时,搜索引擎会非常智能地检测出你的拼写错误,并且用对应的正确单词来进行搜索。作为一名软件开发工程师,你是否想过,这个功能是怎么实现的呢?
如何量化两个字符串的相似度?
计算机只认识数字,所以要解答开篇的问题,我们就要先来看,如何量化两个字符串之间的相似程度呢?有一个非常著名的量化方法,那就是编辑距离(Edit Distance)。
顾名思义,编辑距离指的就是,将一个字符串转化成另一个字符串,需要的最少编辑操作次数(比如增加一个字符、删除一个字符、替换一个字符)。编辑距离越大,说明两个字符串的相似程度越小;相反,编辑距离就越小,说明两个字符串的相似程度越大。对于两个完全相同的字符串来说,编辑距离就是 0。
根据所包含的编辑操作种类的不同,编辑距离有多种不同的计算方式,比较著名的有莱文斯坦距离(Levenshtein distance)和最长公共子串长度(Longest common substring length)。其中,莱文斯坦距离允许增加、删除、替换字符这三个编辑操作,最长公共子串长度只允许增加、删除字符这两个编辑操作。
而且,莱文斯坦距离和最长公共子串长度,从两个截然相反的角度,分析字符串的相似程度。莱文斯坦距离的大小,表示两个字符串差异的大小;而最长公共子串的大小,表示两个字符串相似程度的大小。
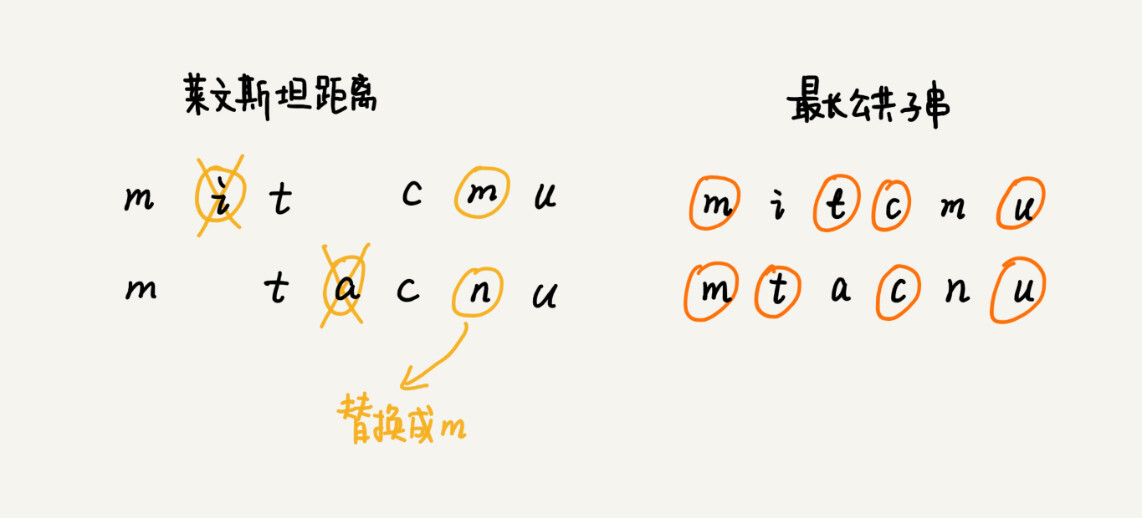
关于这两个计算方法,我举个例子给你说明一下。这里面,两个字符串 mitcmu 和 mtacnu 的莱文斯坦距离是 3,最长公共子串长度是 4。
和 LeetCode 72 号题相同 72. 编辑距离
这个问题是求把一个字符串变成另一个字符串,需要的最少编辑次数。整个求解过程,涉及多个决策阶段,我们需要依次考察一个字符串中的每个字符,跟另一个字符串中的字符是否匹配,匹配的话如何处理,不匹配的话又如何处理。所以,这个问题符合多阶段决策最优解模型。
我们前面讲了,贪心、回溯、动态规划可以解决的问题,都可以抽象成这样一个模型。要解决这个问题,我们可以先看一看,用最简单的回溯算法,该如何来解决。
回溯是一个递归处理的过程。如果 a[i]与 b[j]匹配,我们递归考察 a[i+1]和 b[j+1]。如果 a[i]与 b[j]不匹配,那我们有多种处理方式可选:
-
可以删除 a[i],然后递归考察 a[i+1]和 b[j];
-
可以删除 b[j],然后递归考察 a[i]和 b[j+1];
-
可以在 a[i]前面添加一个跟 b[j]相同的字符,然后递归考察 a[i]和 b[j+1];
-
可以在 b[j]前面添加一个跟 a[i]相同的字符,然后递归考察 a[i+1]和 b[j];
-
可以将 a[i]替换成 b[j],或者将 b[j]替换成 a[i],然后递归考察 a[i+1]和 b[j+1]。
将上面的思路翻译为代码:
func minDistance(word1 string, word2 string) int {
if len(word1) == 0 && len(word2) == 0 {
return 0
}
minDist = math.MaxInt64
backtrack(0, 0, 0, word1, word2)
return minDist
}
var minDist int
func backtrack(i, j, dist int, w1, w2 string) {
if i == len(w1) || j == len(w2) {
if i < len(w1) {
dist += len(w1) - i
}
if j < len(w2) {
dist += len(w2) - j
}
if dist < minDist {
minDist = dist
}
return
}
if w1[i] == w2[j] {
backtrack(i+1, j+1, dist, w1, w2)
} else {
dist++
backtrack(i+1, j, dist, w1, w2)
backtrack(i, j+1, dist, w1, w2)
backtrack(i+1, j+1, dist, w1, w2)
}
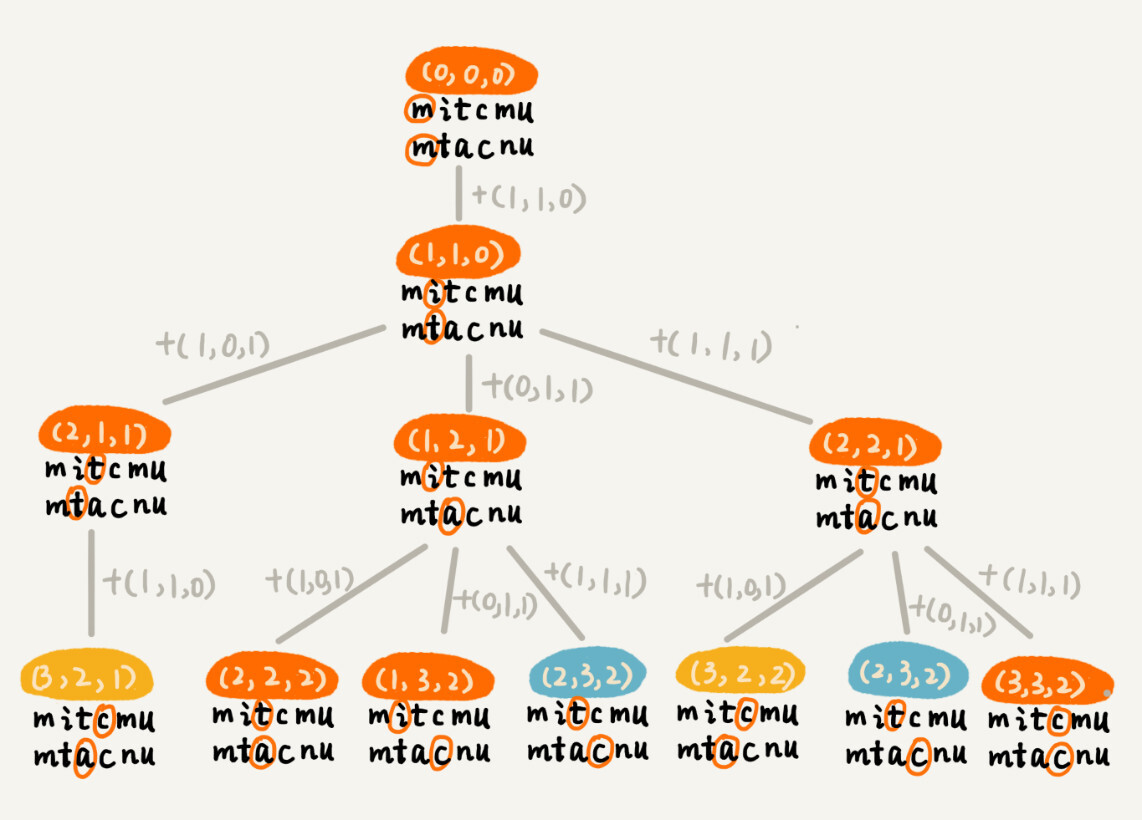
}根据回溯算法的代码实现,我们可以画出递归树,看是否存在重复子问题。如果存在重复子问题,那我们就可以考虑能否用动态规划来解决;如果不存在重复子问题,那回溯就是最好的解决方法。
在递归树中,每个节点代表一个状态,状态包含三个变量 (i, j, edist),其中,edist 表示处理到 a[i]和 b[j]时,已经执行的编辑操作的次数。
在递归树中,(i, j) 两个变量重复的节点很多,比如 (3, 2) 和 (2, 3)。对于 (i, j) 相同的节点,我们只需要保留 edist 最小的,继续递归处理就可以了,剩下的节点都可以舍弃。所以,状态就从 (i, j, edist) 变成了 (i, j, min_edist),其中 min_edist 表示处理到 a[i]和 b[j],已经执行的最少编辑次数。
在前面提到的矩阵最短路径问题中,到达状态 (i, j) 只能通过 (i-1, j) 或 (i, j-1) 两个状态转移过来,而今天这个问题,状态 (i, j) 可能从 (i-1, j),(i, j-1),(i-1, j-1) 三个状态中的任意一个转移过来。
题目给定了两个单词,设为 A 和 B ,设 D 为状态转移表。当我们获得 D[i][j-1],D[i-1][j] 和 D[i-1][j-1] 的值之后就可以计算出 D[i][j]。
D[i][j-1] 为 A 的前 i 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们在 A 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i][j-1] + 1;
D[i-1][j] 为 A 的前 i - 1 个字符和 B 的前 j 个字符编辑距离的子问题。即对于 A 的第 i 个字符,我们在 B 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i-1][j] + 1;
D[i-1][j-1] 为 A 前 i - 1 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们修改 A 的第 i 个字符使它们相同,那么 D[i][j] 最小可以为 D[i-1][j-1] + 1。特别地,如果 A 的第 i 个字符和 B 的第 j 个字符原本就相同,那么我们实际上不需要进行修改操作。在这种情况下,D[i][j] 最小可以为 D[i-1][j-1]。
那么我们可以写出如下的状态转移方程:
- 若
A和B的最后一个字母相同:
- 若
A和B的最后一个字母不同:
func main() {
/*
{ # r o s
# {0, 1, 2, 3},
h {1, 1, 2, 3},
o {2, 2, 1, 2},
r {3, 2, 2, 2},
s {4, 3, 3, 2},
e {5, 4, 4, 3},
}
*/
minDistance("horse", "ros")
}
func minDistance(word1 string, word2 string) int {
n, m := len(word1), len(word2)
// 有一个是空串
if n * m == 0 {
return n + m
}
// 初始化 dp
dp := make([][]int, n+1)
for i := range dp {
dp[i] = append(dp[i], make([]int, m+1)...)
}
for i := 0; i < n+1; i++ { // 初始化 第 0 列
// 相当于对 word1 执行 i 次删除操作
dp[i][0] = i
}
for j := 0; j < m+1; j++ { // 初始化 第 0 行
// 相当于对 word1执行 j 次插入操作
dp[0][j] = j
}
for i := 1; i < n+1; i++ {
for j := 1; j < m+1; j++ {
left := dp[i][j-1] + 1
up := dp[i-1][j] + 1
left_up := dp[i-1][j-1]
if word1[i-1] != word2[j-1] {
left_up++
}
dp[i][j] = min(left, min(left_up, up))
}
}
return dp[n][m]
}
func min(x, y int) int {
if x <= y {
return x
}
return y
}和 LeetCode 1143 号题相同 1143. 最长公共子序列
前面我们讲到,最长公共子串作为编辑距离中的一种,只允许增加、删除字符两种编辑操作。从名字上,你可能觉得它看起来跟编辑距离没什么关系。实际上,从本质上来说,它表征的也是两个字符串之间的相似程度。
这个问题的解决思路,跟莱文斯坦距离的解决思路非常相似,也可以用动态规划解决。我刚刚已经详细讲解了莱文斯坦距离的动态规划解决思路,所以,针对这个问题,我直接定义状态,然后写状态转移方程。
我们先来看回溯的处理思路。我们从 a[0]和 b[0]开始,依次考察两个字符串中的字符是否匹配。
-
如果 a[i]与 b[j]互相匹配,我们将最大公共子串长度加一,并且继续考察 a[i+1]和 b[j+1]。
-
如果 a[i]与 b[j]不匹配,最长公共子串长度不变,这个时候,有两个不同的决策路线:
- 删除 a[i],或者在 b[j]前面加上一个字符 a[i],然后继续考察 a[i+1]和 b[j];
- 删除 b[j],或者在 a[i]前面加上一个字符 b[j],然后继续考察 a[i]和 b[j+1]。
func longestCommonSubsequence(text1 string, text2 string) int {
maxDist = math.MinInt64
t1, t2 = text1, text2
n, m = len(text1), len(text2)
backtrack(0, 0, 0)
return maxDist
}
var(
maxDist int
t1, t2 string
n, m int
)
func backtrack(i, j, dist int) {
if i == n || j == m {
if dist > maxDist {
maxDist = dist
}
return
}
if t1[i] == t2[j] {
backtrack(i+1, j+1, dist+1)
} else {
backtrack(i+1, j, dist)
backtrack(i, j+1, dist)
}
}状态转移方程:
- 若
A和B的最后一个字母不同:
- 若
A和B的最后一个字母相同:
func main() {
/*
{ a c e
a {1, 1, 1},
b {1, 1, 1},
c {1, 2, 2},
d {1, 2, 2},
e {1, 2, 3},
}
*/
longestCommonSubsequence("abcde", "ace")
}
func longestCommonSubsequence(text1 string, text2 string) int {
n, m := len(text1), len(text2)
if n * m == 0 {
return 0
}
// 如果字母不同:dp(i, j) = max(dp(i-1, j), dp(i, j-1))
// 如果字母相同:dp(i, j) = dp[i-1][j-1] + 1
dp := make([][]int, n)
for i := range dp {
dp[i] = append(dp[i], make([]int, m)...)
}
for i := 0; i < n; i++ {
if text1[i] == text2[0] {
dp[i][0] = 1
} else if i != 0 {
dp[i][0] = dp[i-1][0]
}
}
for j := 0; j < m; j++ {
if text1[0] == text2[j] {
dp[0][j] = 1
} else if j != 0 {
dp[0][j] = dp[0][j-1]
}
}
for i := 1; i < n; i++ {
for j := 1; j < m; j++ {
if text1[i] == text2[j] {
dp[i][j] = dp[i-1][j-1] + 1
} else {
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
}
}
}
return dp[n-1][m-1]
}
func max(x, y int) int {
if x >= y {
return x
}
return y
}当用户在搜索框内,输入一个拼写错误的单词时,我们就拿这个单词跟词库中的单词一一进行比较,计算编辑距离,将编辑距离最小的单词,作为纠正之后的单词,提示给用户。
这就是拼写纠错最基本的原理。不过,真正用于商用的搜索引擎,拼写纠错功能显然不会就这么简单。一方面,单纯利用编辑距离来纠错,效果并不一定好;另一方面,词库中的数据量可能很大,搜索引擎每天要支持海量的搜索,所以对纠错的性能要求很高。
针对纠错效果不好的问题,我们有很多种优化思路,我这里介绍几种。
-
我们并不仅仅取出编辑距离最小的那个单词,而是取出编辑距离最小的 TOP 10,然后根据其他参数,决策选择哪个单词作为拼写纠错单词。比如使用搜索热门程度来决定哪个单词作为拼写纠错单词。
-
我们还可以用多种编辑距离计算方法,比如今天讲到的两种,然后分别编辑距离最小的 TOP 10,然后求交集,用交集的结果,再继续优化处理。
-
我们还可以通过统计用户的搜索日志,得到最常被拼错的单词列表,以及对应的拼写正确的单词。搜索引擎在拼写纠错的时候,首先在这个最常被拼错单词列表中查找。如果一旦找到,直接返回对应的正确的单词。这样纠错的效果非常好。
-
我们还有更加高级一点的做法,引入个性化因素。针对每个用户,维护这个用户特有的搜索喜好,也就是常用的搜索关键词。当用户输入错误的单词的时候,我们首先在这个用户常用的搜索关键词中,计算编辑距离,查找编辑距离最小的单词。
针对纠错性能方面,我们也有相应的优化方式。我讲两种分治的优化思路。
-
如果纠错功能的 TPS 不高,我们可以部署多台机器,每台机器运行一个独立的纠错功能。当有一个纠错请求的时候,我们通过负载均衡,分配到其中一台机器,来计算编辑距离,得到纠错单词。
-
如果纠错系统的响应时间太长,也就是,每个纠错请求处理时间过长,我们可以将纠错的词库,分割到很多台机器。当有一个纠错请求的时候,我们就将这个拼写错误的单词,同时发送到这多台机器,让多台机器并行处理,分别得到编辑距离最小的单词,然后再比对合并,最终决定出一个最优的纠错单词。