Skip to content

Latest commit

 

History

History
565 lines (423 loc) · 12 KB

binaryTree.md

File metadata and controls

565 lines (423 loc) · 12 KB

二叉树

数据结构定义

//Definition for a binary tree node.
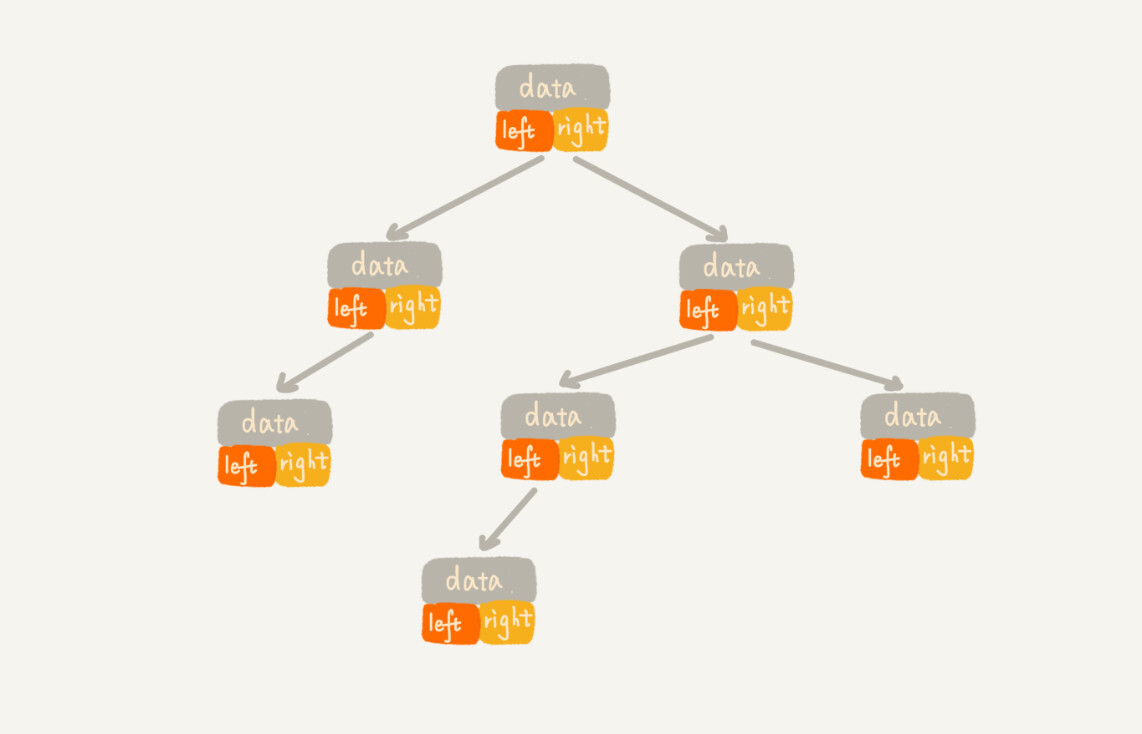
type TreeNode struct {
	Val int
	Left *TreeNode
	Right *TreeNode
}

简介

二叉树的遍历最常见的就是采用广度优先搜索和深度优先搜索进行遍历，最简洁的解法往往是递归，但可能堆栈空间溢出。

此章至少需要的预备知识：

概念

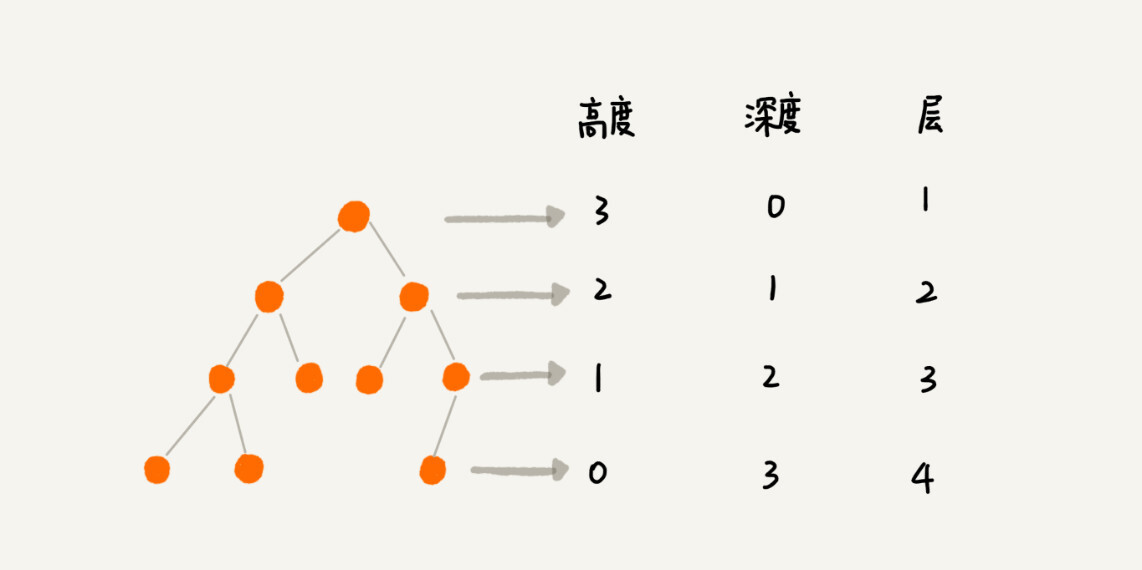
高度（Height）：

节点的高度 = 节点到叶子节点的最长路径（边数）

树的高度 = 根节点的高度

深度（Depth）：

节点的深度 = 根节点到这个节点所经历的边的个数

层（Level）：

节点的层数 = 节点的深度 + 1

img

满二叉树：

叶子节点全部都在最底层，除叶子节点之外，每个节点都有左右两个节点。

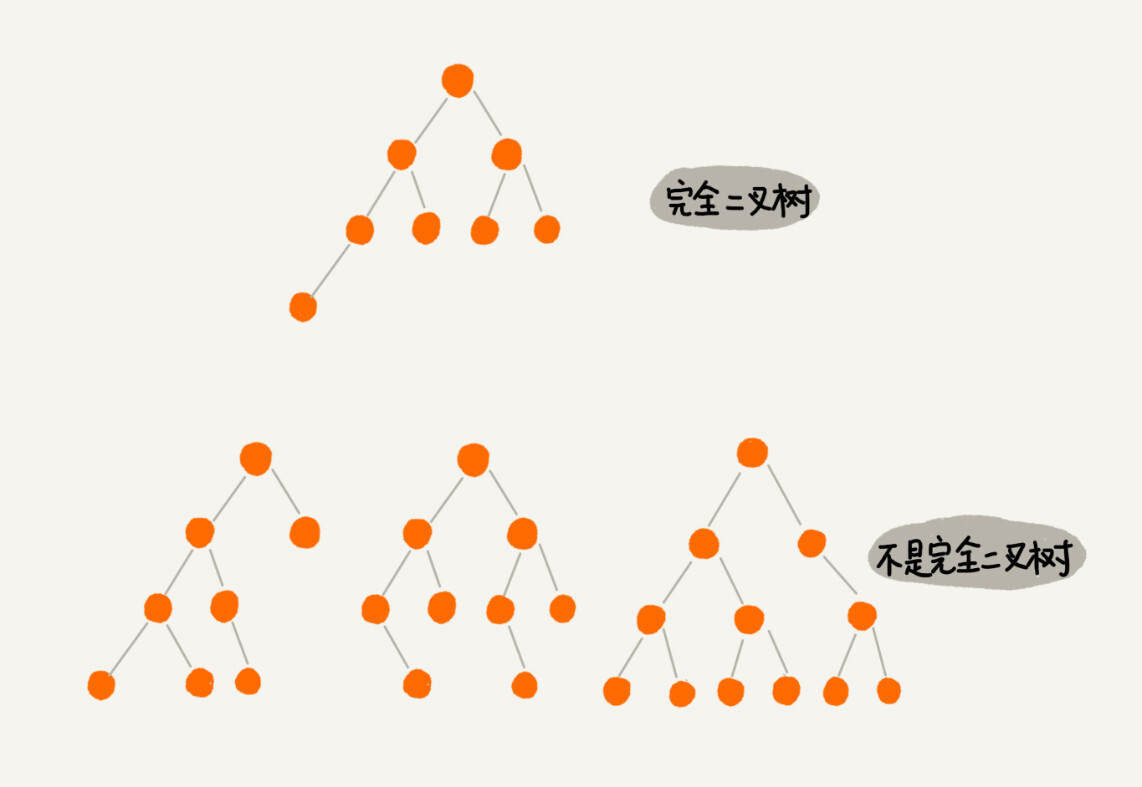
完全二叉树：

叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大。

对比图如下：

img

二叉树的存储

链式存储法

img

顺序存储法

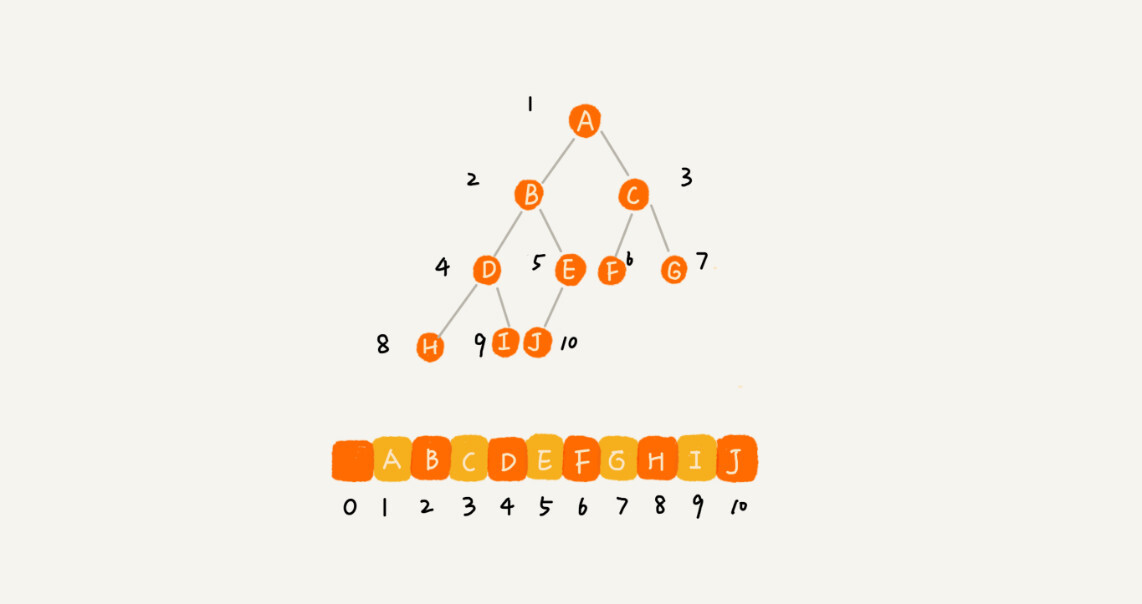
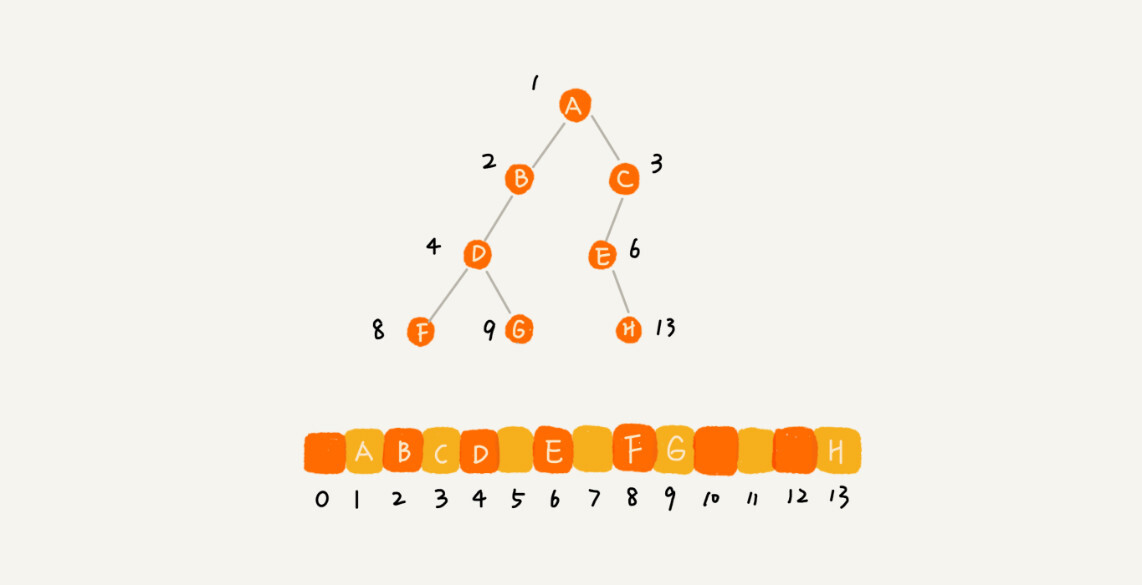
我们把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 * i = 2 的位置，右子节点存储在 2 * i + 1 = 3 的位置。以此类推，B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。

img

如果节点 X 存储在数组中下标为 i 的位置，下标为 2 * i 的位置存储的就是左子节点，下标为 2 * i + 1 的位置存储的就是右子节点。反过来，下标为 i/2 的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为 1 的位置），这样就可以通过下标计算，把整棵树都串起来。

不过，我刚刚举的例子是一棵完全二叉树，所以仅仅**“浪费”**了一个下标为 0 的存储位置。如果是非完全二叉树，其实会浪费比较多的数组存储空间。你可以看我举的下面这个例子。

img

所以，如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点都靠左的原因。

二叉树的遍历

前序遍历

题目描述

给定一个二叉树，返回它的 前序 遍历。

示例:

输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [1,2,3]

题目分析与代码实现

1. 递归
func preorderTraversal(root *TreeNode) []int {
	ans := []int{}
	ans = helper(root, ans)
	return ans
}
func helper(root *TreeNode, ans []int) []int {
	if root == nil { return ans }
	ans = append(ans, root.Val)
	ans = helper(root.Left, ans)
	ans = helper(root.Right, ans)
	return ans
}
2. 深度优先搜索
func preorderTraversal(root *TreeNode) []int {
	if root == nil { return []int{} }
	ans := []int{}
	stack := make([]*TreeNode, 0)
	stack = append(stack, root)

	for len(stack) != 0 {
		cur := stack[len(stack) - 1]
		stack = stack[:len(stack) - 1]
		ans = append(ans, cur.Val)
		if cur.Right != nil { // 注意这里。需要先遍历右子树，因为在出栈的时候，先进的会后出
			stack = append(stack, cur.Right)
		}
		if cur.Left != nil {
			stack = append(stack, cur.Left)
		}

	}
	return ans
}
3. 莫里斯遍历
// 莫里斯遍历 如果是实时输出，空间复杂度为O(1)
// 而每个前驱节点会被访问两次，时间复杂度为O(N)
func preorderTraversal(root *TreeNode) []int {
	ans := []int{}
	node := root
	for node != nil {
		if node.Left == nil {
			ans = append(ans, node.Val)
			node = node.Right
		} else {
			predecessor := node.Left
			for predecessor.Right != nil && predecessor.Right != node {
				predecessor = predecessor.Right
			}

			if predecessor.Right == nil {
				ans = append(ans, node.Val)
				predecessor.Right = node
				node = node.Left
			} else {
				predecessor.Right = nil
				node = node.Right
			}
		}
	}
	return ans
}

中序遍历

题目描述

题目分析与代码实现

1. 递归
recursiveAlgorithm
func inorderTraversal(root *TreeNode) []int {
	ans := []int{}
	return helper(root, ans)
}

func helper(root *TreeNode, ans []int) []int {
	if root == nil { return ans }
	ans = helper(root.Left, ans)
	ans = append(ans, root.Val)
	ans = helper(root.Right, ans)
	return ans
}
2. 深度优先搜索
func inorderTraversal(root *TreeNode) []int {
	res := []int{}
	stack := make([]*TreeNode, 0)
	curr := root
	for curr != nil || len(stack) != 0 {
		for curr != nil {
			stack = append(stack, curr)
			curr = curr.Left
		}
		curr = stack[len(stack) - 1]
		stack = stack[:len(stack) - 1]
		res = append(res, curr.Val)
		curr = curr.Right
	}
	return res
}

后序遍历

题目描述

题目分析与代码实现

1. 递归
func postorderTraversal(root *TreeNode) []int {
	ans := []int{}
	return helper(root, ans)
}

func helper(root *TreeNode, ans []int) []int {
	if root == nil { return ans }
	ans = helper(root.Left, ans)
	ans = helper(root.Right, ans)
	ans = append(ans, root.Val)
	return ans
}
2. 深度优先搜索
func postorderTraversal(root *TreeNode) []int {
	ans := []int{}
	return dfs(root, ans)
}
func dfs(root *TreeNode, ans []int) []int {
	stack := make([]*TreeNode, 0)
	cur := root
	visited := make(map[*TreeNode]bool)
	for cur != nil || len(stack) != 0 {
		for !visited[cur] && cur != nil {
			stack = append(stack, cur)
			visited[cur] = true
			cur = cur.Left
		}
		if len(stack) == 0 {
			break
		}
		cur = stack[len(stack) - 1]
		if !visited[cur.Right] && cur.Right != nil {
			cur = cur.Right
		} else {
			ans = append(ans, cur.Val)
			stack = stack[:len(stack) - 1]
		}
	}
	return ans
}

或者

func postorderTraversal(root *TreeNode) []int {
	ans := []int{}
	stack := make([]*TreeNode, 0)
	if root == nil { return ans }
	stack = append(stack, root)
	for len(stack) != 0 {
		node := stack[len(stack) - 1]
		stack = stack[:len(stack) - 1]
		ans = append([]int{node.Val}, ans...)
		if node.Left != nil {
			stack = append(stack, node.Left)
		}
		if node.Right != nil {
			stack = append(stack, node.Right)
		}
	}
	return ans
}

层序遍历

题目描述

题目分析与代码实现

广度优先搜索
func levelOrder(root *TreeNode) [][]int {
	ans := [][]int{}
	if root == nil { return ans }
	queue := make([]*TreeNode, 0)
	queue = append(queue, root)
	for floor := 0; len(queue) != 0; floor++ {
		ans = append(ans, []int{})
		length := len(queue)
		for i := 0; i < length; i++ {
			cur := queue[0]
			queue = queue[1:]
			ans[floor] = append(ans[floor], cur.Val)
			if cur.Left != nil {
				queue = append(queue, cur.Left)
			}
			if cur.Right != nil {
				queue = append(queue, cur.Right)
			}
		}
	}
	return ans
}

高频面试题

简介

部分引用自：面试前准备：二叉树高频面试题和答案

该节并不只是二叉树的题目，若遇到不会题目，请先前去学习相应数据结构。

二叉树的最大深度

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    left := maxDepth(root.Left)
    right := maxDepth(root.Right)
    return int(math.Max(float64(left),float64(right)) + 1)
}

二叉树的最小深度

func minDepth(root *TreeNode) int {
	if root == nil {
		return 0
	}
	return getMin(root)
}

func getMin(root *TreeNode) int {
	if root == nil {
		return math.MaxInt64
	}
	if root.Left == nil && root.Right == nil {
		return 1
	}
	left := getMin(root.Left)
	right := getMin(root.Right)
	return int(math.Min(float64(left), float64(right))) + 1
}

二叉树中的节点个数

func numOfTreeNode(root *TreeNode) {
    if root == nil {
        return 0
    }
    left := numOfTreeNode(root.Left)
    right := numsOfTreeNode(root.Right)
    return left + right + 1
}

二叉树中叶子节点的个数

func numsOfNoChildNode(root *TreeNode) int {
    if root == nil {
        return 0
    }
    if root.Left == nil && root.Right == nil {
        return 1
    }
    left := numsOfNoChildNode(root.Left)
    right := numsOfNoChildNode(root.Right)
    return left + right
}

二叉树中第k层节点的个数

func numsOfkLevelTreeNode(root *TreeNode, k int) int {
    if root == nil || k < 1 {
        return 0
    }
    if k == 1 {
        return 1
    }
    left := numsOfkLevelTreeNode(root.Left, k-1)
    right := numsOfkLevelTreeNode(root.Right, k-1)
    return left + right
}

验证二叉搜索树

思路一：利用中序遍历

func isValidBST(root *TreeNode) bool {
    if root == nil {
        return true
    }
    pre := -math.MaxInt64
    return isValid(root, &pre)
}

func isValid(root *TreeNode, pre *int) bool {
    if root == nil {
        return true
    }
    if !isValid(root.Left, pre) {
        return false
    }
    if root.Val <= *pre {
        return false
    }
    *pre = root.Val
    if !isValid(root.Right, pre) {
        return false
    }
    return true
}

思路二：利用二叉搜索树特性

func isValidBST(root *TreeNode) bool {
	return isValidBSTByBorder(root, math.MaxInt64, math.MinInt64)
}

func isValidBSTByBorder(root *TreeNode, max,min int) bool {
	if root == nil {
		return true
	}

	if root.Val >= max || root.Val <= min {
		return false
	}
	
	return isValidBSTByBorder(root.Left, root.Val, min) &&
    	isValidBSTByBorder(root.Right, max, root.Val)
}

验证平衡二叉树

方法一：自顶向下的递归

func isBalanced(root *TreeNode) bool {
    if root == nil {
        return true
    }
    left := maxDepth(root.Left)
    right := maxDepth(root.Right)
    return int(math.Abs(float64(left - right))) <= 1 && isBalanced(root.Left) && isBalanced(root.Right)
}

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    left := maxDepth(root.Left)
    right := maxDepth(root.Right)
    return int(math.Max(float64(left), float64(right))) + 1
}

方法二：自底向上的递归

func isBalanced(root *TreeNode) bool {
    return helper(root) >= 0
}

func helper(root *TreeNode) int {
    if root == nil {
        return 0
    }
    left := helper(root.Left)
    right := helper(root.Right)
    // 一旦有一个结点的左右子树高度不平衡，-1会直接传递到函数调用的最上层
    if left == -1 || right == -1 || int(math.Abs(float64(left - right))) > 1 {
        return -1
    }
    return int(math.Max(float64(left), float64(right))) + 1
}

验证二叉树是否对称

func isSymmetric(root *TreeNode) bool {
    return isMirror(root, root)
}

func isMirror(left, right *TreeNode) bool {
    if left == nil && right == nil { return true }
    if left == nil || right == nil { return false }
    if left.Val != right.Val { return false }
    return isMirror(left.Left, right.Right) && isMirror(left.Right, right.Left)
}

引用

数据结构与算法之美