03_freegames.md

A biblioteca freegames

Como já apresentado anteriormente, além de possuir os jogos, o Free Python Games também inclui uma biblioteca com alguns utilitários úteis. Por isso, que após instalado o pacote freegames, podemos executar a importação abaixo no Python:

>>> import freegames

Abra o seu intepretador Python para executar este e os demais exemplos.

Os utilitários da biblioteca freegames podem ser organizados em 3 categorias:

1. Funções de desenho
2. Funções auxiliares
3. Vetores

Funções de desenho

• freegames.line(a, b, x, y)

Desenha uma linha do ponto (a, b) até o ponto (x, y).

>>> freegames.line(10, 10, 100, 100)

• freegames.square(x, y, size, name)

Desenha um quadrado a partir do ponto (x, y) com lado de tamanho size e preenchido com cor de nome name. O quadrado é direcionado para a direita e para cima.

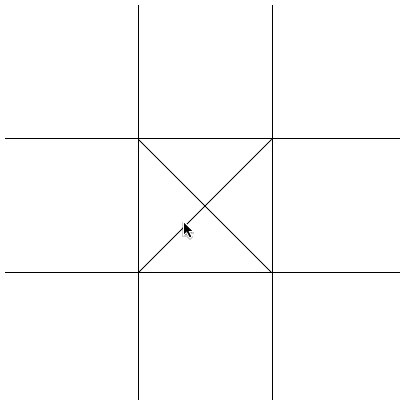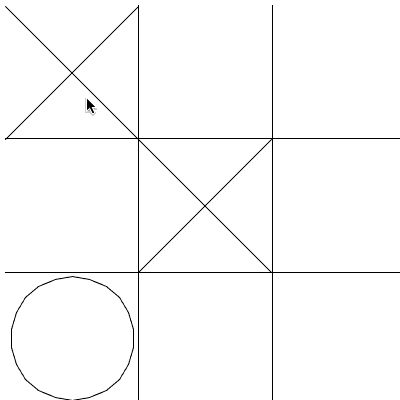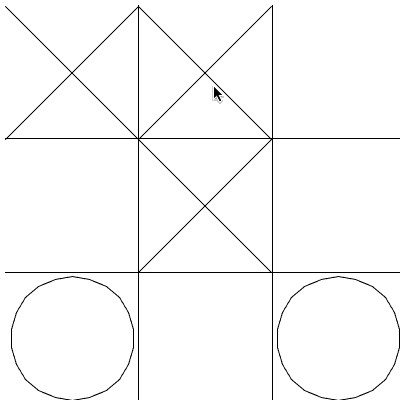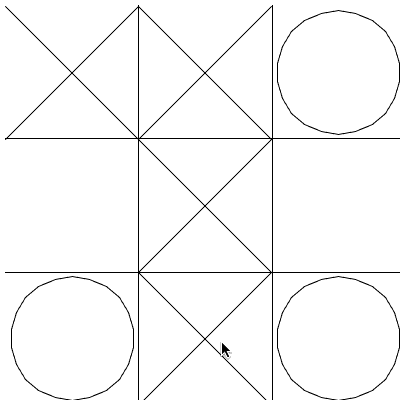
>>> freegames.square(-50, 20, 100, 'blue')

Funções auxiliares

Para calcular posições

Considere a grade de um Jogo-da-Velha abaixo:

Perceba que é preciso identificar a área clicada para fazer a jogada (preencher com x ou bola), porém quando o evento de clique ocorre (registrado pelo onscreenclick) o que se tem é apenas as coordenadas x e y, sendo necessários alguns cálculos para se identificar a àrea clicada, e de forma mais específica o ponto da tela em que o desenho deve começar.

Imagine que para desenhar a grade, é feito um deslocamento para a esquerda de 100 e que cada casa tem um tamanho de 100. Portanto, o lado esquerdo mais extremo das casas serão: -100, 0 e 100. Assim, os valores que identificam a casa clicada estão em intervalos que são:

• Casa esquerda: valores de -100 a -1
• Casa do meio: valores de 0 a 99
• Casa da direita: valores de 100 a 199

Obviamente, o mesmo raciocinío e cálculo precisam ser feito para o deslocamento vertical.

Para facilitar esses cálculos a biblioteca provê a função floor.

• freegames.floor(value, size, offset=200)

Retorna o piso do valor value, dado um tamanho size e deslocamento offset.

Essa função é melhor compreendida com o diagrama da reta numérica:

        -200  -30   140   310   480
<----a----|--b--|--c--|--d--|--e--|----f---->

O diagrama mostra um deslocamento de 200 (parâmetro offset da função), indicado pelo valor -200 mais a esquerda, e um tamanho de 170 (parâmetro size da função), denotado pelas distâncias entre -200 e -30, e todas as outras distâncias entre dois pontos adjacentes indicados no diagrama.

Já o parâmetro value está representado no diagrama pelas letras a, b, c, d e f. Quaisquer que seja o valor desse parâmetro, para essa configuração, o retorno da função será o ponto identificado à esquerda. Ou seja floor(b) é -200, floor(c) é -30 e assim por diante. Considere ainda que a reta é virtualmente infinita para ambos os lados e os marcos continuam se repetindo a cada 170.

Veja, e execute, alguns exemplos concretos:

>>> freegames.floor(-170, 170, 200)
-200.0
>>> freegames.floor(-31, 170, 200)
-200.0
>>> freegames.floor(-30, 170, 200)
-30.0
>>> freegames.floor(310, 170, 200)
310.0
>>> freegames.floor(410, 170, 200)
310.0
>>> freegames.floor(510, 170, 200)
480.0

Para carregar imagens

Turtle possui suporte para carregamento e exibição de imagens. Free Python Games utiliza esse recurso em alguns jogos, por exemplo no Memory. Para carregar a imagem é necessário ter o caminho completo do arquivo, daí a utilidade de uma função que você passa apenas o nome do arquivo, e função retorna o caminho completo, que será utilizado pelas funções de carregamento do arquivo para exibição.

• freegames.path(filename)

Retorna o caminho completo para filename na módulo freegames.

As figuras podem ser utilizadas tanto para se colocar uma imagem de fundo, quanto definir o formato da tartatura, com a função shape, já utilizada anteriormente. Porém, para novos formatos, é preciso antes registrar este novo formato com register_shape (ou addshape), conforme apresentado a seguir.

>>> car = freegames.path('car.gif')
>>> car
'/home/adorilson/.local/lib/python3.10/site-packages/freegames/car.gif'
>>> import turtle
>>> turtle.register_shape(car)
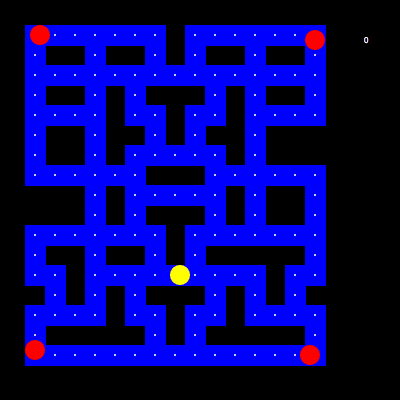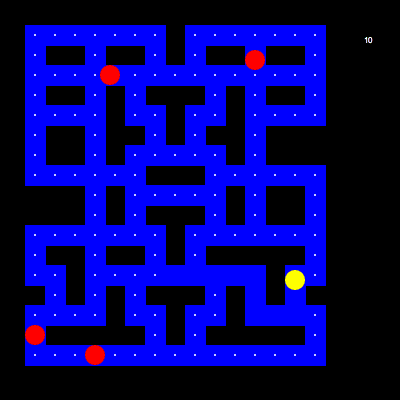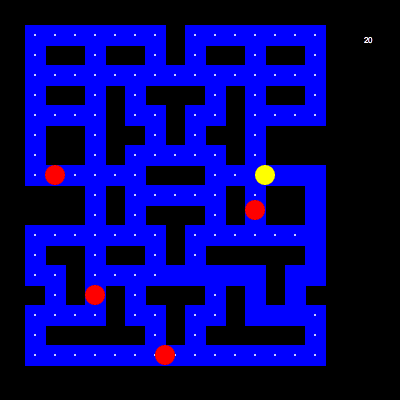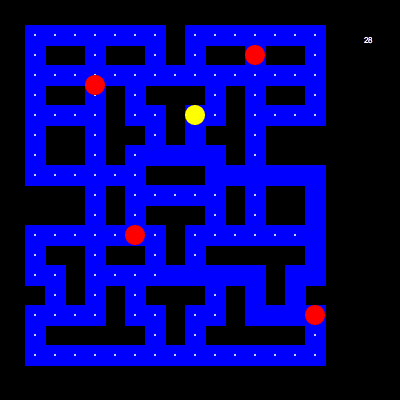
>>> turtle.shape(car)

Vetores

Se você observar o jogo Pacman e considerar que cada ator móvel do jogo (Pacman e os fantasmas) possuem sua localização (x, y) armazenadas em variáveis, deverá ser fácil deduzir que essa variáveis estão constantemente sendo atualizadas.

Para tal, Free Python Games utiliza as operações do ente matemático chamado de vetor.

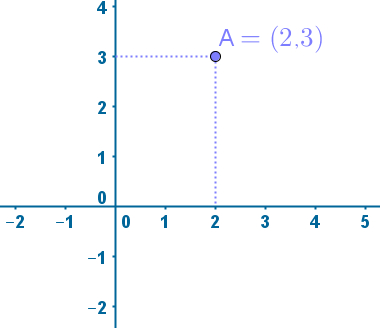
Considere um ponto qualquer no sistema de coordenadas utilizadas por Turtle, por exemplo o ponto A(2, 3), conforme imagem abaixo.

Imagine um segmento de reta que vai da origem (0, 0) até o ponto A, este segmento de reta é o que chamamos de vetor. Na realidade, vetor é o cojunto formato por todos os segmentos orientados que possuem a mesma direção, o mesmo sentido e o mesmo comprimento, mas consideramos apenas um elemento desse conjunto por simplificação - veja as referências para o conceito matemático completo.

Diversas operações são definidas para vetores, mas talvez a mais importante delas para o nosso contexto seja a operação de soma de vetores. A soma de dois vetores pode ser feita pela regra do paralelograma.

Assim: a+b = ( ax + bx, ay + by )

Vetores de referências

Considere o vetor V e os vetores Vy e Vx na figura abaixo. V é um vetor nosso qualquer no plano, enquanto que Vy e Vx são vetores de referência, com valores respectivos de (0, 1) e (1, 0). Assim, se eu desejo que o meu vetor V se desloque para cima irei somá-lo com Vy, se desejo que se o deslocamento seja para a direita, a soma é com Vx. De forma análoga, existem também os vetores para descolamento nas sentidos contrários. Tais vetores estão definidos em Free Python Games e são utilizados para a movimentação dos atores móveis dos jogos.

Classe vector

Free Python Games define a classe freegames.vector(x, y) para encapsular as operações de vetores.

• Criação e representação do vetor

>>> from freegames import vector
>>> v = vector(3, 4)
>>> v
vector(3, 4)

• Atributos x e y

>>> v = vector(1, 2)
>>> v.x
1
>>> v.x = 3
>>> v.x
3
>>> v.y
2
>>> v.y = 5
>>> v.y
5

• Comparação de igualdade

>>> v = vector(1, 2)
>>> w = vector(1, 2)
>>> v == w
True

• Comparação de desigualdade

>>> v = vector(1, 2)
>>> w = vector(3, 4)
>>> v != w
True

• Comprimento (distância até a origem)

>>> v = vector(3, 4)
>>> abs(v)
5.0

• Adição de vetores (com outro vetor e com um número)

>>> v = vector(1, 2)
>>> w = vector(3, 4)
>>> v + w
vector(4, 6)
>>> w + v
vector(4, 6)
>>> v + 1
vector(2, 3)
>> 2.0 + v
vector(3.0, 4.0)

• Subtração (com outro vetor ou com um número)

>>> v = vector(1, 2)
>>> w = vector(3, 4)
>>> v - w
vector(-2, -2)
>>> v - 1
vector(0, 1)

• Multiplicação (por outro vetor e por um número)

>>> v = vector(1, 2)
>>> w = vector(3, 4)
>>> v * w
vector(3, 8)
>>> v * 2
vector(2, 4)
>>> 3.0 * v
vector(3.0, 6.0)

• Divisão (por outro vetor e por um número)

>>> v = vector(2, 4)
>>> w = vector(4, 8)
>>> v /= w
>>> v
vector(0.5, 0.5)
>>> v /= 2
>>> v
vector(0.25, 0.25)

• Inversão

>>> v = vector(1, 2)
>>> -v
vector(-1, -2)

• Move um vetor (mudança interna no vetor)

>>> v = vector(1, 2)
>>> w = vector(3, 4)
>>> v.move(w)
>>> v
vector(4, 6)
>>> v.move(3)
>>> v
vector(7, 9)

• Cópia

>>> v = vector(1, 2)
>>> w = v.copy()
>>> v is w
False

• Rotação (sentido anti-horário a partir de um ângulo, mudança interna no vetor)

>>> v = vector(1, 2)
>>> v.rotate(90)
>>> v == vector(-2, 1)
True

• Escala (mudança interna no vetor)

>>> v = vector(1, 2)
>>> w = vector(3, 4)
>>> v.scale(w)
>>> v
vector(3, 8)
>>> v.scale(0.5)
>>> v
vector(1.5, 4.0)

Referências

Vetor (Matemática)

Vetores no Plano e no Espaço. | 01. Álgebra Linear.

Anterior | Próximo