Skip to content

Latest commit

 

History

History
168 lines (106 loc) · 7.35 KB

3108.minimum-cost-walk-in-weighted-graph.md

File metadata and controls

168 lines (106 loc) · 7.35 KB
Raw

题目地址(3108. 带权图里旅途的最小代价 - 力扣（LeetCode）)

https://leetcode.cn/problems/minimum-cost-walk-in-weighted-graph/

题目描述

给你一个 n 个节点的带权无向图，节点编号为 0 到 n - 1 。

给你一个整数 n 和一个数组 edges ，其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条权值为 wi 的无向边。

在图中，一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点，且图中存在连接旅途中相邻节点的边。注意，一趟旅途可能访问同一条边或者同一个节点多次。

如果旅途开始于节点 u ，结束于节点 v ，我们定义这一趟旅途的 代价 是经过的边权按位与 AND 的结果。换句话说，如果经过的边对应的边权为 w0, w1, w2, ..., wk ，那么代价为w0 & w1 & w2 & ... & wk ，其中 & 表示按位与 AND 操作。

给你一个二维数组 query ，其中 query[i] = [si, ti] 。对于每一个查询，你需要找出从节点开始 si ，在节点 ti 处结束的旅途的最小代价。如果不存在这样的旅途，答案为 -1 。

返回数组 answer ，其中 answer[i] 表示对于查询 i 的 最小 旅途代价。

 

示例 1：

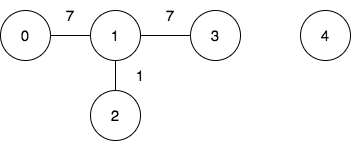
输入：n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]

输出：[1,-1]

解释：

第一个查询想要得到代价为 1 的旅途，我们依次访问：0->1（边权为 7 ）1->2 （边权为 1 ）2->1（边权为 1 ）1->3 （边权为 7 ）。

第二个查询中，无法从节点 3 到节点 4 ，所以答案为 -1 。

示例 2：

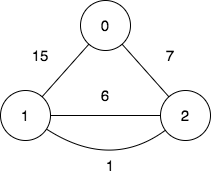
输入：n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]

输出：[0]

解释：

第一个查询想要得到代价为 0 的旅途，我们依次访问：1->2（边权为 1 ），2->1（边权 为 6 ），1->2（边权为 1 ）。

 

提示：

  • 1 <= n <= 105
  • 0 <= edges.length <= 105
  • edges[i].length == 3
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 0 <= wi <= 105
  • 1 <= query.length <= 105
  • query[i].length == 2
  • 0 <= si, ti <= n - 1

前置知识

公司

  • 暂无

思路

由于代价是按位与 ，而不是相加，因此如果 s 到 t 我们尽可能多的走，那么 and 的值就会越来越小。这是因为两个数的与一定不比这两个数大。

  • 考虑如果 s 不能到达 t，那么直接返回 -1。
  • 如果 s 到 t 可以到达，说明 s 和 t 在同一个联通集。对于联通集外的点，我们无法到达。而对于联通集内的点，我们可以到达。前面说了，我们尽可能多的做，因此对于联通集内的点，我们都走一遍。答案就是联通集合中的边的 and 值。

使用并查集模板可以解决，主要改动点在于 union 方法。大家可以对照我的并查集标准模板看看有什么不同。

关键点

代码

  • 语言支持：Python3

Python3 Code:

class UF:
  def __init__(self, M):
      self.parent = {}
      self.cnt = 0
      self.all_and = {}
      # 初始化 parent，size 和 cnt
      # Initialize parent, size and cnt
      for i in range(M):
          self.parent[i] = i
          self.cnt += 1
          self.all_and[i] = 2 ** 30 - 1 # 也可以初始化为 -1

  def find(self, x):
      if x != self.parent[x]:
          self.parent[x] = self.find(self.parent[x])
          return self.parent[x]
      return x
  def union(self, p, q, w):
    #   if self.connected(p, q): return # 这道题对于联通的情况不能直接 return，具体可以参考示例 2. 环的存在
      leader_p = self.find(p)
      leader_q = self.find(q)
      self.parent[leader_p] = leader_q
      # p 连通块的 and 值为 w1，q 连通块的 and 值为 w2，合并后就是 w1 & w2 & w
      self.all_and[leader_p] = self.all_and[leader_q] = self.all_and[leader_p] & w & self.all_and[leader_q]
      self.cnt -= 1
  def connected(self, p, q):
      return self.find(p) == self.find(q)
        
class Solution:
    def minimumCost(self, n: int, edges: List[List[int]], query: List[List[int]]) -> List[int]:
        g = [[] for _ in range(n)]
        uf = UF(n)
        for x, y, w in edges:
            g[x].append((y, w))
            g[y].append((x, w))
            uf.union(x, y, w)

        ans = []
        for s, t in query:
            if not uf.connected(s, t):
                ans.append(-1)
            else:
                ans.append(uf.all_and[uf.parent[s]])
        return ans

复杂度分析

令 m 为 edges 长度。

  • 时间复杂度：$O(m + n)$
  • 空间复杂度：$O(m + n)$

此题解由 力扣刷题插件 自动生成。

力扣的小伙伴可以关注我，这样就会第一时间收到我的动态啦~

以上就是本文的全部内容了。大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 40K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。

关注公众号力扣加加，努力用清晰直白的语言还原解题思路，并且有大量图解，手把手教你识别套路，高效刷题。