动态规划是一个从其他行业借鉴过来的词语。
它的大概意思先将一件事情分成若干阶段,然后通过阶段之间的转移达到目标。由于转移的方向通常是多个,因此这个时候就需要决策选择具体哪一个转移方向。
动态规划所要解决的事情通常是完成一个具体的目标,而这个目标往往是最优解。并且:
- 阶段之间可以进行转移,这叫做动态。
- 达到一个可行解(目标阶段) 需要不断地转移,那如何转移才能达到最优解?这叫规划。
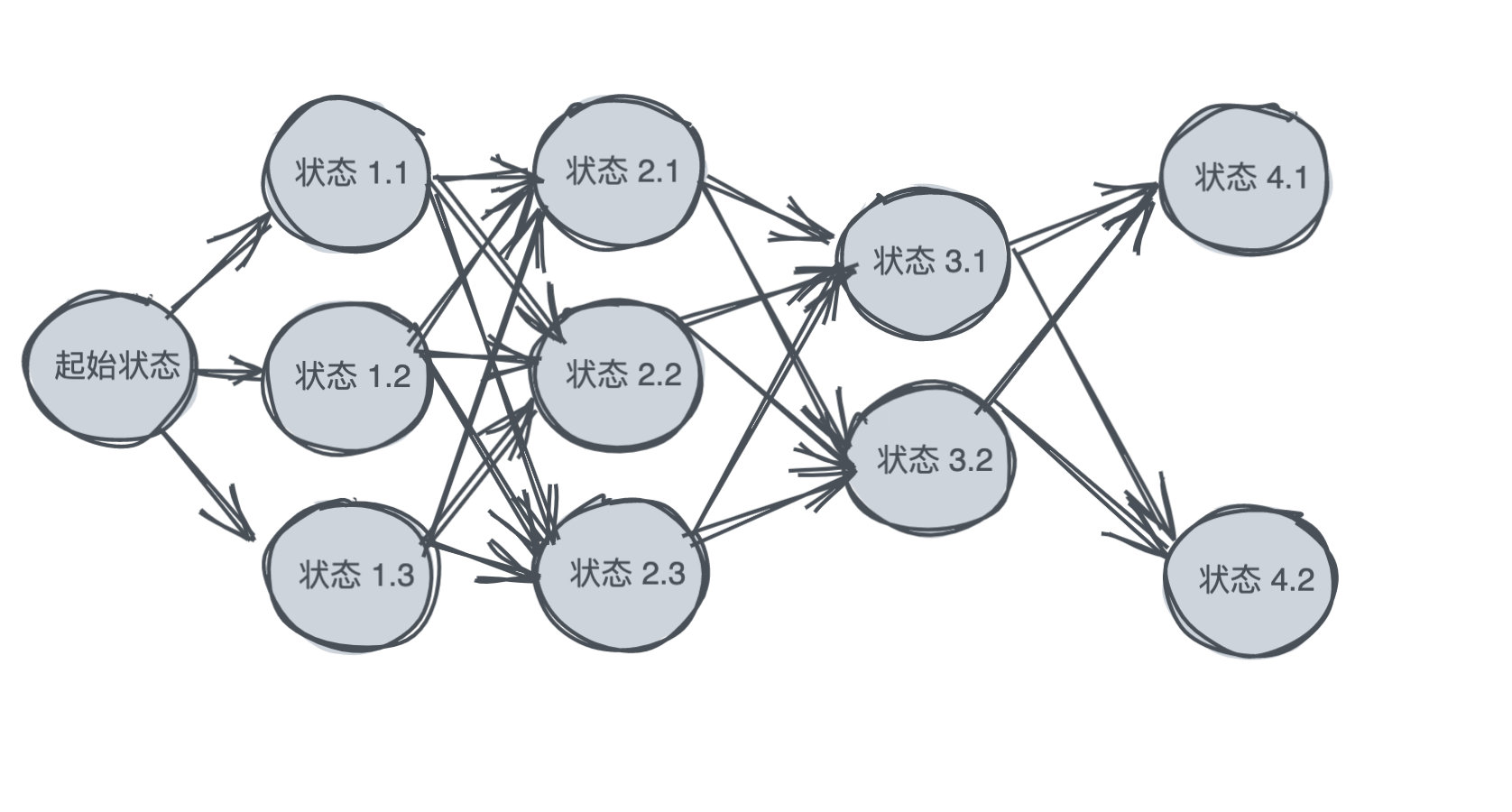
每个阶段抽象为状态(用圆圈来表示),状态之间可能会发生转化(用箭头表示)。可以画出类似如下的图:
那我们应该做出如何的决策序列才能使得结果最优?换句话说就是每一个状态应该如何选择到下一个具体状态,并最终到达目标状态。这就是动态规划研究的问题。
每次决策实际上不会考虑之后的决策,而只会考虑之前的状态。 形象点来说,其实是走一步看一步这种短视思维。为什么这种短视可以来求解最优解呢?那是因为:
- 我们将所有可能的转移全部模拟了一遍,最后挑了一个最优解。
- 无后向性(这个我们后面再说,先卖个关子)
而如果你没有模拟所有可能,而直接走了一条最优解,那就是贪心算法了。
没错,动态规划刚开始就是来求最优解的。只不过有的时候顺便可以求总的方案数等其他东西,这其实是动态规划的副产物。
好了,我们把动态规划拆成两部分分别进行解释,或许你大概知道了动态规划是一个什么样的东西。但是这对你做题并没有帮助。那算法上的动态规划究竟是个啥呢?
在算法上,动态规划和查表的递归(也称记忆化递归) 有很多相似的地方。我建议大家先从记忆化递归开始学习。本文也先从记忆化递归开始,逐步讲解到动态规划。
那么什么是递归?什么是查表(记忆化)?让我们慢慢来看。
递归是指在函数中调用函数自身的方法。
有意义的递归通常会把问题分解成规模缩小的同类子问题,当子问题缩小到寻常的时候,我们可以直接知道它的解。然后通过建立递归函数之间的联系(转移)即可解决原问题。
是不是和分治有点像? 分治指的是将问题一分为多,然后将多个解合并为一。而这里并不是这个意思。
一个问题要使用递归来解决必须有递归终止条件(算法的有穷性),也就是说递归会逐步缩小规模到寻常。
虽然以下代码也是递归,但由于其无法结束,因此不是一个有效的算法:
def f(x):
return x + f(x - 1)上面的代码除非外界干预,否则会永远执行下去,不会停止。
因此更多的情况应该是:
def f(n):
if n == 1: return 1
return n + f(n - 1)使用递归通常可以使代码短小,有时候也更可读。算法中使用递归可以很简单地完成一些用循环不太容易实现的功能,比如二叉树的左中右序遍历。
递归在算法中有非常广泛的使用,包括现在日趋流行的函数式编程。
递归在函数式编程中地位很高。 纯粹的函数式编程中没有循环,只有递归。
实际上,除了在编码上通过函数调用自身实现递归。我们也可以定义递归的数据结构。比如大家所熟知的树,链表等都是递归的数据结构。
Node {
value: any; // 当前节点的值
children: Array<Node>; // 指向其儿子
}如上代码就是一个多叉树的定义形式,可以看出 children 就是 Node 的集合类,这就是一种递归的数据结构。
本文中所提到的记忆化递归中的递归函数实际上指的是特殊的递归函数,即在普通的递归函数上满足以下几个条件:
- 递归函数不依赖外部变量
- 递归函数不改变外部变量
满足这两个条件有什么用呢?这是因为我们需要函数给定参数,其返回值也是确定的。这样我们才能记忆化。关于记忆化,我们后面再讲。
如果大家了解函数式编程,实际上这里的递归其实严格来说是函数式编程中的函数。如果不了解也没关系,这里的递归函数其实就是数学中的函数。
我们来回顾一下数学中的函数:
在一个变化过程中,假设有两个变量 x、y,如果对于任意一个 x 都有唯一确定的一个 y 和它对应,那么就称 x 是自变量,y 是 x 的函数。x 的取值范围叫做这个函数的定义域,相应 y 的取值范围叫做函数的值域 。
而本文所讲的所有递归都是指的这种数学中的函数。
比如上面的递归函数:
def f(x):
if x == 1: return 1
return x + f(x - 1)- x 就是自变量,x 的所有可能的返回值构成的集合就是定义域。
- f(x) 就是函数。
- f(x) 的所有可能的返回值构成的集合就是值域。
自变量也可以有多个,对应递归函数的参数可以有多个,比如 f(x1, x2, x3)。
通过函数来描述问题,并通过函数的调用关系来描述问题间的关系就是记忆化递归的核心内容。
每一个动态规划问题,实际上都可以抽象为一个数学上的函数。这个函数的自变量集合就是题目的所有取值,值域就是题目要求的答案的所有可能。我们的目标其实就是填充这个函数的内容,使得给定自变量 x,能够唯一映射到一个值 y。(当然自变量可能有多个,对应递归函数参数可能有多个)
解决动态规划问题可以看成是填充函数这个黑盒,使得定义域中的数并正确地映射到值域。
递归并不是算法,它是和迭代对应的一种编程方法。只不过,我们通常借助递归去分解问题而已。比如我们定义一个递归函数 f(n),用 f(n) 来描述问题。就和使用普通动态规划 f[n] 描述问题是一样的,这里的 f 是 dp 数组。
为了大家能够更好地对本节内容进行理解,我们通过一个例子来切入:
一个人爬楼梯,每次只能爬 1 个或 2 个台阶,假设有 n 个台阶,那么这个人有多少种不同的爬楼梯方法?
思路:
由于第 n 级台阶一定是从 n - 1 级台阶或者 n - 2 级台阶来的,因此到第 n 级台阶的数目就是 到第 n - 1 级台阶的数目加上到第 n - 2 级台阶的数目。
递归代码:
function climbStairs(n) {
if (n === 1) return 1;
if (n === 2) return 2;
return climbStairs(n - 1) + climbStairs(n - 2);
}我们用一个递归树来直观感受以下(每一个圆圈表示一个子问题):
红色表示重复的计算。即 Fib(N-2) 和 Fib(N-3) 都被计算了两次,实际上计算一次就够了。比如第一次计算出了 Fib(N-2) 的值,那么下次再次需要计算 Fib(N-2)的时候,可以直接将上次计算的结果返回。之所以可以这么做的原因正是前文提到的我们的递归函数是数学中的函数,也就是说参数一定,那么返回值也一定不会变,因此下次如果碰到相同的参数,我们就可以将上次计算过的值直接返回,而不必重新计算。这样节省的时间就等价于重叠子问题的个数。
以这道题来说,本来需要计算
代码上,我们可以使用一个 hashtable 去缓存中间计算结果,从而省去不必要的计算。
我们使用记忆化来改造上面的代码:
memo = {}
def climbStairs(n):
if n == 1:return 1
if n == 2: return 2
if n in memo: return memo[n]
ans = func(n - 1) + func(n-2)
memo[n] = ans
return ans
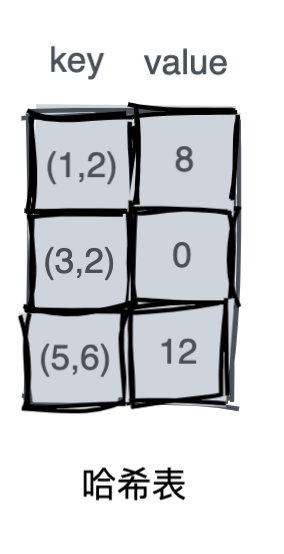
climbStairs(10)这里我使用了一个名为 memo 的哈希表来存储递归函数的返回值,其中 key 为参数,value 为递归函数的返回值。
key 的形式为 (x, y),表示的是一个元祖。通常动态规划的参数有多个,我们就可以使用元祖的方式来记忆化。或者也可采取多维数组的形式。对于上图来说,就可使用二维数组来表示。
大家可以通过删除和添加代码中的 memo 来感受一下记忆化的作用。
使用递归函数的优点是逻辑简单清晰,缺点是过深的调用会导致栈溢出。这里我列举了几道算法题目,这几道算法题目都可以用递归轻松写出来:
-
递归实现 sum
-
二叉树的遍历
-
走楼梯问题
-
汉诺塔问题
-
杨辉三角
递归中如果存在重复计算(我们称重叠子问题,下文会讲到),那就是使用记忆化递归(或动态规划)解题的强有力信号之一。可以看出动态规划的核心就是使用记忆化的手段消除重复子问题的计算,如果这种重复子问题的规模是指数或者更高规模,那么记忆化递归(或动态规划)带来的收益会非常大。
为了消除这种重复计算,我们可使用查表的方式。即一边递归一边使用“记录表”(比如哈希表或者数组)记录我们已经计算过的情况,当下次再次碰到的时候,如果之前已经计算了,那么直接返回即可,这样就避免了重复计算。下文要讲的动态规划中 DP 数组其实和这里“记录表”的作用是一样的。
如果你刚开始接触递归, 建议大家先去练习一下递归再往后看。一个简单练习递归的方式是将你写的迭代全部改成递归形式。比如你写了一个程序,功能是“将一个字符串逆序输出”,那么使用迭代将其写出来会非常容易,那么你是否可以使用递归写出来呢?通过这样的练习,可以让你逐步适应使用递归来写程序。
当你已经适应了递归的时候,那就让我们继续学习动态规划吧!
讲了这么多递归和记忆化,终于到了我们的主角登场了。
我们先来学习动态规划最重要的两个概念:最优子结构和无后效性。
其中:
- 无后效性决定了是否可使用动态规划来解决。
- 最优子结构决定了具体如何解决。
动态规划常常适用于有重叠子问题和最优子结构性质的问题。前面讲了重叠子问题,那么最优子结构是什么?这是我从维基百科找的定义:
如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。最优子结构性质为动态规划算法解决问题提供了重要线索。
举个例子:如果考试中的分数定义为 f,那么这个问题就可以被分解为语文,数学,英语等子问题。显然子问题最优的时候,总分这个大的问题的解也是最优的。
再比如 01 背包问题:定义 f(weights, values, capicity)。如果我们想要求 f([1,2,3], [2,2,4], 10) 的最优解。从左到右依次考虑是否将每一件物品加入背包。我们可以将其划分为如下子问题:
不将第三件物品装进背包(即仅考虑前两件),也就是 f([1,2], [2,2], 10)- 和
将第三件物品装进背包,也就是 f([1,2,3], [2,2,4], 10) (即仅考虑前两件的情况下装满容量为 10 - 3 = 7 的背包) 等价于 4 + f([1,2], [2,2], 7),其中 4 为第三件物品的价值,7 为装下第三件物品后剩余可用空间,由于我们仅考虑前三件,因此前两件必须装满 10 - 3 = 7 才行。
显然这两个问题还是复杂,我们需要进一步拆解。不过,这里不是讲如何拆解的。
原问题 f([1,2,3], [2,2,4], 10) 等于以上两个子问题的最大值。只有两个子问题都是最优的时候整体才是最优的,这是因为子问题之间不会相互影响。
即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。
继续以上面两个例子来说。
- 数学考得高不能影响英语(现实其实可能影响,比如时间一定,投入英语多,其他科目就少了)。
- 背包问题中 f([1,2,3], [2,2,4], 10) 选择是否拿第三件物品,不应该影响是否拿前面的物品。比如题目规定了拿了第三件物品之后,第二件物品的价值就会变低或变高)。这种情况就不满足无后向性。
动态规划的中心点是什么?如果让我说的话,那就是定义状态。
动态规划解题的第一步就是定义状态。定义好了状态,就可以画出递归树,聚焦最优子结构写转移方程就好了,因此我才说状态定义是动态规划的核心,动态规划问题的状态确实不容易看出。
但是一旦你能把状态定义好了,那就可以顺藤摸瓜画出递归树,画出递归树之后就聚焦最优子结构就行了。但是能够画出递归树的前提是:对问题进行划分,专业点来说就是定义状态。那怎么才能定义出状态呢?
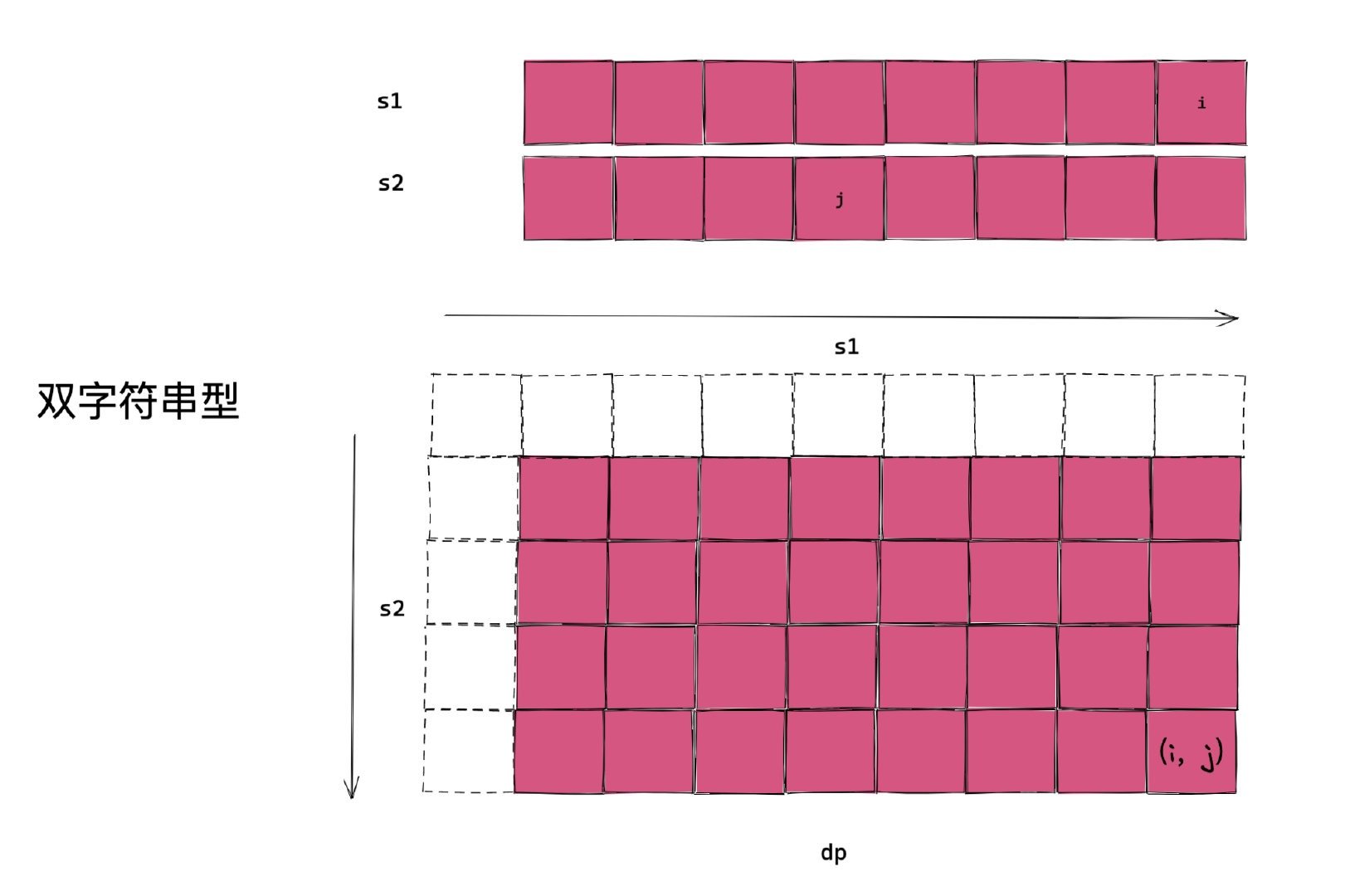
好在状态的定义都有特点的套路。 比如一个字符串的状态,通常是 dp[i] 表示字符串 s 以 i 结尾的 ....。 比如两个字符串的状态,通常是 dp[i][j] 表示字符串 s1 以 i 结尾,s2 以 j 结尾的 ....。
也就是说状态的定义通常有不同的套路,大家可以在做题的过程中进行学习和总结。但是这种套路非常多,那怎么搞定呢?
说实话,只能多练习,在练习的过程中总结套路。具体的套路参考后面的动态规划的题型 部分内容。之后大家就可以针对不同的题型,去思考大概的状态定义方向。
两个例子
关于状态定义,真的非常重要,以至于我将其列为动态规划的核心。因此我觉得有必要举几个例子来进行说明。我直接从力扣的动态规划专题中抽取前两道给大家讲讲。
第一道题:《5. 最长回文子串》难度中等
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
示例 3:
输入:s = "a"
输出:"a"
示例 4:
输入:s = "ac"
输出:"a"
提示:
1 <= s.length <= 1000
s 仅由数字和英文字母(大写和/或小写)组成
这道题入参是一个字符串,那我们要将其转化为规模更小的子问题,那无疑就是字符串变得更短的问题,临界条件也应该是空字符串或者一个字符这样。
因此:
- 一种定义状态的方式就是 f(s1),含义是字符串 s1 的最长回文子串,其中 s1 就是题目中的字符串 s 的子串,那么答案就是 f(s)。
- 由于规模更小指的是字符串变得更短,而描述字符串我们也可以用两个变量来描述,这样实际上还省去了开辟字符串的开销。两个变量可以是起点索引 + 子串长度,也可以是终点索引 + 子串长度,也可以是起点坐标 + 终点坐标。随你喜欢,这里我就用起点坐标 + 终点坐标。那么状态定义就是 f(start, end),含义是子串 s[start:end+1]的最长回文子串,那么答案就是 f(0, len(s) - 1)
s[start:end+1] 指的是包含 s[start],而不包含 s[end+1] 的连续子串。
这无疑是一种定义状态的方式,但是一旦我们这样去定义就会发现:状态转移方程会变得难以确定(实际上很多动态规划都有这个问题,比如最长上升子序列问题)。那究竟如何定义状态呢?我会在稍后的状态转移方程继续完成这道题。我们先来看下一道题。
第二道题:《10. 正则表达式匹配》难度困难
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa" p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa" p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab" p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:s = "aab" p = "c*a*b"
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:s = "mississippi" p = "mis*is*p*."
输出:false
提示:
0 <= s.length <= 20
0 <= p.length <= 30
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
保证每次出现字符 * 时,前面都匹配到有效的字符
这道题入参有两个, 一个是 s,一个是 p。沿用上面的思路,我们有两种定义状态的方式。
- 一种定义状态的方式就是 f(s1, p1),含义是 p1 是否可匹配字符串 s1,其中 s1 就是题目中的字符串 s 的子串,p1 就是题目中的字符串 p 的子串,那么答案就是 f(s, p)。
- 另一种是 f(s_start, s_end, p_start, p_end),含义是子串 p1[p_start:p_end+1] 是否可以匹配字符串 s[s_start:s_end+1],那么答案就是 f(0, len(s) - 1, 0, len(p) - 1)
而这道题实际上我们也可采用更简单的状态定义方式,不过基本思路都是差不多的。我仍旧卖个关子,后面讲转移方程再揭晓。
搞定了状态定义,你会发现时间空间复杂度都变得很明显了。这也是为啥我反复强调状态定义是动态规划的核心。
时间空间复杂度怎么个明显法了呢?
首先空间复杂度,我刚才说了动态规划其实就是查表的暴力法,因此动态规划的空间复杂度打底就是表的大小。再直白一点就是上面的哈希表 memo 的大小。而 memo的大小基本就是状态的个数。状态个数是多少呢? 这不就取决你状态怎么定义了么?比如上面的 f(s1, p1) 。状态的多少是多少呢?很明显就是每个参数的取值范围大小的笛卡尔积。s1 的所有可能取值有 len(s) 种,p1 的所有可能有 len(p)种,那么总的状态大小就是 len(s) * len(p)。那空间复杂度是
我说空间复杂度打底是状态个数, 这里暂时先不考虑状态压缩的情况。
其次是时间复杂度。时间复杂度就比较难说了。但是由于我们无论如何都要枚举所有状态,因此时间复杂度打底就是状态总数。以上面的状态定义方式,时间复杂度打底就是$O(m * n)$。
如果你枚举每一个状态都需要和 s 的每一个字符计算一下,那时间复杂度就是
以上面的爬楼梯的例子来说,我们定义状态 f(n) 表示到达第 n 级台阶的方法数,那么状态总数就是 n,空间复杂度和时间复杂度打底就是
再举个例子:62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
这道题是和上面的爬楼梯很像,只不过从一维变成了二维,我把它叫做二维爬楼梯,类似的换皮题还很多,大家慢慢体会。
这道题我定义状态为 f(i, j) 表示机器人到达点 (i,j) 的总的路径数。那么状态总数就是 i 和 j 的取值的笛卡尔积,也就是 m * n 。
总的来说,动态规划的空间和时间复杂度打底就是状态的个数,而状态的个数通常是参数的笛卡尔积,这是由动态规划的无后向性决定的。
临界条件是比较容易的
当你定义好了状态,剩下就三件事了:
-
临界条件
-
状态转移方程
-
枚举状态
在上面讲解的爬楼梯问题中,如果我们用 f(n) 表示爬 n 级台阶有多少种方法的话,那么:
f(1) 与 f(2) 就是【边界】
f(n) = f(n-1) + f(n-2) 就是【状态转移公式】
我用动态规划的形式表示一下:
dp[0] 与 dp[1] 就是【边界】
dp[n] = dp[n - 1] + dp[n - 2] 就是【状态转移方程】
可以看出记忆化递归和动态规划是多么的相似。
实际上临界条件相对简单,大家只有多刷几道题,里面就有感觉。困难的是找到状态转移方程和枚举状态。这两个核心点的都建立在已经抽象好了状态的基础上。比如爬楼梯的问题,如果我们用 f(n) 表示爬 n 级台阶有多少种方法的话,那么 f(1), f(2), ... 就是各个独立的状态。
搞定了状态的定义,那么我们来看下状态转移方程。
动态规划中当前阶段的状态往往是上一阶段状态和上一阶段决策的结果。这里有两个关键字,分别是 :
- 上一阶段状态
- 上一阶段决策
也就是说,如果给定了第 k 阶段的状态 s[k] 以及决策 choice(s[k]),则第 k+1 阶段的状态 s[k+1] 也就完全确定,用公式表示就是:s[k] + choice(s[k]) -> s[k+1], 这就是状态转移方程。需要注意的是 choice 可能有多个,因此每个阶段的状态 s[k+1]也会有多个。
继续以上面的爬楼梯问题来说,爬楼梯问题由于上第 n 级台阶一定是从 n - 1 或者 n - 2 来的,因此 上第 n 级台阶的数目就是 上 n - 1 级台阶的数目加上 n - 2 级台阶的数目。
上面的这个理解是核心, 它就是我们的状态转移方程,用代码表示就是 f(n) = f(n - 1) + f(n - 2)。
实际操作的过程,有可能题目和爬楼梯一样直观,我们不难想到。也可能隐藏很深或者维度过高。 如果你实在想不到,可以尝试画图打开思路,这也是我刚学习动态规划时候的方法。当你做题量上去了,你的题感就会来,那个时候就可以不用画图了。
比如我们定义了状态方程,据此我们定义初始状态和目标状态。然后聚焦最优子结构,思考每一个状态究竟如何进行扩展使得离目标状态越来越近。
如下图所示:
理论差不多先这样,接下来来几个实战消化一下。
ok,接下来是解密环节。上面两道题我们都没有讲转移方程,我们在这里补上。
第一道题:《5. 最长回文子串》难度中等。上面我们的两种状态定义都不好,而我可以在上面的基础上稍微变动一点就可以使得转移方程变得非常好写。这个技巧在很多动态题目都有体现,比如最长上升子序列等,需要大家掌握。
以上面提到的 f(start, end) 来说,含义是子串 s[start:end+1]的最长回文子串。表示方式我们不变,只是将含义变成子串 s[start:end+1]的最长回文子串,且必须包含 start 和 end。经过这样的定义,实际上我们也没有必要定义 f(start, end)的返回值是长度了,而仅仅是布尔值就行了。如果返回 true, 则最长回文子串就是 end - start + 1,否则就是 0。
这样转移方程就可以写为:
f(i,j)=f(i+1,j−1) and s[i] == s[j]
第二道题:《10. 正则表达式匹配》难度困难。
以我们分析的 f(s_start, s_end, p_start, p_end) 来说,含义是子串 p1[p_start:p_end+1] 是否可以匹配字符串 s[s_start:s_end+1]。
实际上,我们可以定义更简单的方式,那就是 f(s_end, p_end),含义是子串 p1[:p_end+1] 是否可以匹配字符串 s[:s_end+1]。也就是说固定起点为索引 0,这同样也是一个很常见的技巧,请务必掌握。
这样转移方程就可以写为:
- if p[j] 是小写字母,是否匹配取决于 s[i] 是否等于 p[j]:
- if p[j] == '.',一定可匹配:
f(i,j)=f(i-1,j−1)
- if p[j] == '*',表示 p 可以匹配 s 第 j−1 个字符匹配任意次:
相信你能分析到这里,写出代码就不是难事了。具体代码可参考我的力扣题解仓库,咱就不在这里讲了。
注意到了么?所有的状态转移方程我都使用了上述的数学公式来描述。没错,所有的转移方程都可以这样描述。我建议大家做每一道动态规划题目都写出这样的公式,起初你可能觉得很烦麻烦。不过相信我,你坚持下去,会发现自己慢慢变强大。就好像我强烈建议你每一道题都分析好复杂度一样。动态规划不仅要搞懂转移方程,还要自己像我那样完整地用数学公式写出来。
是不是觉得状态转移方程写起来麻烦?这里我给大家介绍一个小技巧,那就是使用 latex,latex 语法可以方便地写出这样的公式。另外西法还贴心地写了一键生成动态规划转移方程公式的功能,帮助大家以最快速度生成公诉处。 插件地址:https://leetcode-pp.github.io/leetcode-cheat/?tab=solution-template
状态转移方程实在是没有什么灵丹妙药,不同的题目有不同的解法。状态转移方程同时也是解决动态规划问题中最最困难和关键的点,大家一定要多多练习,提高题感。接下来,我们来看下不那么困难,但是新手疑问比较多的问题 - 如何枚举状态。
当然状态转移方程可能不止一个, 不同的转移方程对应的效率也可能大相径庭,这个就是比较玄学的话题了,需要大家在做题的过程中领悟。
前面说了如何枚举状态,才能不重不漏是枚举状态的关键所在。
- 如果是一维状态,那么我们使用一层循环可以搞定。
for i in range(1, n + 1):
pass- 如果是两维状态,那么我们使用两层循环可以搞定。
for i in range(1, m + 1):
for j in range(1, n + 1):
pass- 。。。
但是实际操作的过程有很多细节比如:
- 一维状态我是先枚举左边的还是右边的?(从左到右遍历还是从右到左遍历)
- 二维状态我是先枚举左上边的还是右上的,还是左下的还是右下的?
- 里层循环和外层循环的位置关系(可以互换么)
- 。。。
其实这个东西和很多因素有关,很难总结出一个规律,而且我认为也完全没有必要去总结规律。
不过这里我还是总结了一个关键点,那就是:
- 如果你没有使用滚动数组的技巧,那么遍历顺序取决于状态转移方程。比如:
for i in range(1, n + 1):
dp[i] = dp[i - 1] + 1那么我们就需要从左到右遍历,原因很简单,因为 dp[i] 依赖于 dp[i - 1],因此计算 dp[i] 的时候, dp[i - 1] 需要已经计算好了。
二维的也是一样的,大家可以试试。
- 如果你使用了滚动数组的技巧,则怎么遍历都可以,但是不同的遍历意义通常不不同的。比如我将二维的压缩到了一维:
for i in range(1, n + 1):
for j in range(1, n + 1):
dp[j] = dp[j - 1] + 1;这样是可以的。 dp[j - 1] 实际上指的是压缩前的 dp[i][j - 1]
而:
for i in range(1, n + 1):
# 倒着遍历
for j in range(n, 0, -1):
dp[j] = dp[j - 1] + 1;这样也是可以的。 但是 dp[j - 1] 实际上指的是压缩前的 dp[i - 1][j - 1]。因此实际中采用怎么样的遍历手段取决于题目。我特意写了一个 【完全背包问题】套路题(1449. 数位成本和为目标值的最大数字 文章,通过一个具体的例子告诉大家不同的遍历有什么实际不同,强烈建议大家看看,并顺手给个三连。
- 关于里外循环的问题,其实和上面原理类似。
这个比较微妙,大家可以参考这篇文章理解一下 0518.coin-change-2。
关于如何确定临界条件通常是比较简单的,多做几个题就可以快速掌握。
关于如何确定状态转移方程,这个其实比较困难。 不过所幸的是,这些套路性比较强, 比如一个字符串的状态,通常是 dp[i] 表示字符串 s 以 i 结尾的 ....。 比如两个字符串的状态,通常是 dp[i][j] 表示字符串 s1 以 i 结尾,s2 以 j 结尾的 ....。 这样遇到新的题目可以往上套, 实在套不出那就先老实画图,不断观察,提高题感。
关于如何枚举状态,如果没有滚动数组, 那么根据转移方程决定如何枚举即可。 如果用了滚动数组,那么要注意压缩后和压缩前的 dp 对应关系即可。
上面我们用记忆化递归的问题巧妙地解决了爬楼梯问题。 那么动态规划是怎么解决这个问题呢?
答案也是“查表”,我们平常写的 dp table 就是表,其实这个 dp table 和上面的 memo 没啥差别。
而一般我们写的 dp table,数组的索引通常对应记忆化递归的函数参数,值对应递归函数的返回值。
看起来两者似乎没任何思想上的差异,区别的仅仅是写法?? 没错。不过这种写法上的差异还会带来一些别的相关差异,这点我们之后再讲。
如果上面的爬楼梯问题,使用动态规划,代码是怎么样的呢?我们来看下:
function climbStairs(n) {
if (n == 1) return 1;
const dp = new Array(n);
dp[0] = 1;
dp[1] = 2;
for (let i = 2; i < n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[dp.length - 1];
}大家现在不会也没关系,我们将前文的递归的代码稍微改造一下。其实就是将函数的名字改一下:
function dp(n) {
if (n === 1) return 1;
if (n === 2) return 2;
return dp(n - 1) + dp(n - 2);
}经过这样的变化。我们将 dp[n] 和 dp(n) 对比看,这样是不是有点理解了呢? 其实他们的区别只不过是递归用调用栈枚举状态, 而动态规划使用迭代枚举状态。
如果需要多个维度枚举,那么记忆化递归内部也可以使用迭代进行枚举,比如最长上升子序列问题。
动态规划的查表过程如果画成图,就是这样的:
虚线代表的是查表过程
爬楼梯我们并没有必要使用一维数组,而是借助两个变量来实现的,空间复杂度是 O(1)。代码:
function climbStairs(n) {
if (n === 1) return 1;
if (n === 2) return 2;
let a = 1;
let b = 2;
let temp;
for (let i = 3; i <= n; i++) {
temp = a + b;
a = b;
b = temp;
}
return temp;
}之所以能这么做,是因为爬楼梯问题的状态转移方程中当前状态只和前两个状态有关,因此只需要存储这两个即可。 动态规划问题有很多这种讨巧的方式,这个技巧叫做滚动数组。
这道题目是动态规划中最简单的问题了,因为仅涉及到单个因素的变化,如果涉及到多个因素,就比较复杂了,比如著名的背包问题,挖金矿问题等。
对于单个因素的,我们最多只需要一个一维数组即可,对于如背包问题我们需要二维数组等更高维度。
回答上面的问题:记忆化递归和动态规划除了一个用递归一个用迭代,其他没差别。那两者有啥区别呢?我觉得最大的区别就是记忆化递归无法使用滚动数组优化。
不信你用上面的爬楼梯试一下,下面代码如何使用滚动数组优化?
const memo = {};
function dp(n) {
if (n === 1) return 1;
if (n === 2) return 2;
if (n in memo) return memo[n];
const ans = dp(n - 1) + dp(n - 2);
memo[n] = ans;
return ans;
}本质上来说, 记忆化递归采用的方式是 DFS,因此会一条路走到黑,然后返回来继续其他可行的路一口气再次走到黑。而迭代使用的是类似 BFS 的方式,这样一层层访问, � 太远的层可能用不到了,就可以直接抹去,这就是滚动数组的本质。
记忆化调用栈的开销比较大(复杂度不变,你可以认为空间复杂度常数项更大),不过几乎不至于 TLE 或者 MLE。因此我的建议就是没空间优化需求直接就记忆化,否则用迭代 dp。
再次强调一下:
- 如果说递归是从问题的结果倒推,直到问题的规模缩小到寻常。 那么动态规划就是从寻常入手, 逐步扩大规模到最优子结构。
- 记忆化递归和动态规划没有本质不同。都是枚举状态,并根据状态直接的联系逐步推导求解。
- 动态规划性能通常更好。 一方面是递归的栈开销,一方面是滚动数组的技巧。
- 背包 DP(这个我们专门开了一个专题讲)
- 区间 DP
区间类动态规划是线性动态规划的扩展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。令状态
区间 DP 的特点:
合并:即将两个或多个部分进行整合,当然也可以反过来;
特征:能将问题分解为能两两合并的形式;
求解:对整个问题设最优值,枚举合并点,将问题分解为左右两个部分,最后合并两个部分的最优值得到原问题的最优值。
推荐两道题:
关于状压 DP 可以参考下我之前写过的一篇文章: 状压 DP 是什么?这篇题解带你入门
- 数位 DP
数位 DP 通常是这:给定一个闭区间 ,让你求这个区间中满足某种条件的数的总数。
推荐一道题 Increasing-Digits
- 计数 DP 和 概率 DP
这两个我就不多说。因为没啥规律。
之所以列举计数 DP 是因为两个原因:
- 让大家知道确实有这个题型。
- 计数是动态规划的副产物。
概率 DP 比较特殊,概率 DP 的状态转移公式一般是说一个状态有多大的概率从某一个状态转移过来,更像是期望的计算,因此也叫期望 DP。
推荐两道题:
更多题目类型以及推荐题目见刷题插件的学习路线。插件获取方式:公众号力扣加加回复插件。
- 从数组两端同时进行遍历的时候使用记忆化递归方便,其实也就是区间 DP(range dp)。比如石子游戏,再比如这道题 https://binarysearch.com/problems/Make-a-Palindrome-by-Inserting-Characters
如果区间 dp 你的遍历方式大概需要这样:
class Solution:
def solve(self, s):
n = len(s)
dp = [[0] * n for _ in range(n)]
# 右边界倒序遍历
for i in range(n - 1, -1, -1):
# 左边界正序遍历
for j in range(i + 1, n):
# do something
return dp[0][m-1] # 一般都是使用这个区间作为答案如果使用记忆化递归则不需考虑遍历方式的问题。
代码:
class Solution:
def solve(self, s):
@lru_cache(None)
def helper(l, r):
if l >= r:
return 0
if s[l] == s[r]:
return helper(l + 1, r - 1)
return 1 + min(helper(l + 1, r), helper(l, r - 1))
return helper(0, len(s) - 1)- 选择 比较离散的时候,使用记忆化递归更好。比如马走棋盘。
那什么时候不用记忆化递归呢?答案是其他情况都不用。因为普通的 dp table 有一个重要的功能,这个功能记忆化递归是无法代替的,那就是滚动数组优化。如果你需要对空间进行优化,那一定要用 dp table。
理论知识已经差不多了,我们拿一道题来试试手。
我们以一个非常经典的背包问题来练一下手。
题目:322. 零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
这道题的参数有两个,一个是 coins,一个是 amount。
我们可以定义状态为 f(i, j) 表示用 coins 的前 i 项找 j 元需要的最少硬币数。那么答案就是 f(len(coins) - 1, amount)。
由组合原理,coins 的所有选择状态是
减 1 是因为存在 0 元的情况。
明确了这些,我们需要考虑的就是状态如何转移,也就是如何从寻常转移到 f(len(coins) - 1, amount)。
如何确定状态转移方程?我们需要:
- 聚焦最优子结构
- 做选择,在选择中取最优解(如果是计数 dp 则进行计数)
对于这道题来说,我们的选择有两种:
- 选择 coins[i]
- 不选择 coins[i]
这无疑是完备的。只不过仅仅是对 coins 中的每一项进行选择与不选择,这样的状态数就已经是
如果仅仅是这样枚举肯定会超时,因为状态数已经是指数级别了。
而这道题的核心在于 coins[i] 选择与否其实没有那么重要,重要的其实是选择的 coins 一共有多少钱。
因此我们可以定义 f(i, j) 表示选择了 coins 的前 i 项(怎么选的不关心),且组成 j 元需要的最少硬币数。
举个例子来说,比如 coins = [1,2,3] 。那么选择 [1,2] 和 选择 [3] 虽然是不一样的状态,但是我们压根不关心。因为这两者没有区别,我们还是谁对结果贡献大就 pick 谁。
以 coins = [1,2,3], amount = 6 来说,我们可以画出如下的递归树。
(图片来自https://leetcode.com/problems/coin-change/solution/)
因此转移方程就是 min(dp[i-1][j], dp[i][j - coins[i]] + 1),含义就是: min(不选择 coins[i], 选择 coins[i]) 所需最少的硬币数。
用公式表示就是:
amount 表示无解。因为硬币的面额都是正整数,不可能存在一种需要 amount + 1 枚硬币的方案。
代码
记忆化递归:
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
@lru_cache(None)
def dfs(amount):
if amount < 0: return float('inf')
if amount == 0: return 0
ans = float('inf')
for coin in coins:
ans = min(ans, 1 + dfs(amount - coin))
return ans
ans = dfs(amount)
return -1 if ans == float('inf') else ans二维 dp:
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
if amount < 0:
return - 1
dp = [[amount + 1 for _ in range(len(coins) + 1)]
for _ in range(amount + 1)]
# 初始化第一行为0,其他为最大值(也就是amount + 1)
for j in range(len(coins) + 1):
dp[0][j] = 0
for i in range(1, amount + 1):
for j in range(1, len(coins) + 1):
if i - coins[j - 1] >= 0:
dp[i][j] = min(
dp[i][j - 1], dp[i - coins[j - 1]][j] + 1)
else:
dp[i][j] = dp[i][j - 1]
return -1 if dp[-1][-1] == amount + 1 else dp[-1][-1]dp[i][j] 依赖于dp[i][j - 1]和 dp[i - coins[j - 1]][j] + 1) 这是一个优化的信号,我们可以将其优化到一维。
一维 dp(滚动数组优化):
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [amount + 1] * (amount + 1)
dp[0] = 0
for j in range(len(coins)):
for i in range(1, amount + 1):
if i >= coins[j]:
dp[i] = min(dp[i], dp[i - coins[j]] + 1)
return -1 if dp[-1] == amount + 1 else dp[-1]最后推荐几道题目给大家,建议大家分别使用记忆化递归和动态规划来解决。如果使用动态规划,则尽可能使用滚动数组优化空间。
- 0091.decode-ways
- 0139.word-break
- 0198.house-robber
- 0309.best-time-to-buy-and-sell-stock-with-cooldown
- 0322.coin-change
- 0416.partition-equal-subset-sum
- 0518.coin-change-2
本篇文章总结了算法中比较常用的两个方法 - 递归和动态规划。递归的话可以拿树的题目练手,动态规划的话则将我上面推荐的刷完,再考虑去刷力扣的动态规划标签即可。
大家前期学习动态规划的时候,可以先尝试使用记忆化递归解决。然后将其改造为动态规划,这样多练习几次就会有感觉。之后大家可以练习一下滚动数组,这个技巧很有用,并且相对来说比较简单。
动态规划的核心在于定义状态,定义好了状态其他都是水到渠成。
动态规划的难点在于枚举所有状态(不重不漏) 和 寻找状态转移方程。
- oi-wiki - dp 这个资料推荐大家学习,非常全面。只不过更适合有一定基础的人,大家可以配合本讲义食用哦。
另外,大家可以去 LeetCode 探索中的 递归 I 中进行互动式学习。