diff --git a/_site/feed.xml b/_site/feed.xml
index 89934bf..e31c592 100644
--- a/_site/feed.xml
+++ b/_site/feed.xml
@@ -1 +1 @@
-Jekyll2018-08-02T08:16:22-07:00http://localhost:4000/Python for climate scientistsMaterials for Earth science data wranglingBaird
\ No newline at end of file
+Jekyll2018-08-02T08:17:22-07:00http://localhost:4000/Python for climate scientistsMaterials for Earth science data wranglingBaird
\ No newline at end of file
diff --git a/collections/_matplotlib/pcolormesh-grid-fix.md b/collections/_matplotlib/pcolormesh-grid-fix.md
index 107b8a2..82823f6 100644
--- a/collections/_matplotlib/pcolormesh-grid-fix.md
+++ b/collections/_matplotlib/pcolormesh-grid-fix.md
@@ -4,11 +4,11 @@ date: 2018-08-02
order: 1
---
-One of the most frequently recurring frustrations with Matplotlib is how the ```pcolor``` and ```pcolormesh``` functions work. I tend to use ```pcolormesh``` more, since the two functions are practically the same but the latter much faster.
+One recurring frustration that I have with Matplotlib is how the ```pcolor``` and ```pcolormesh``` functions work. (I tend to use ```pcolormesh``` more, since the two functions are practically the same but the latter much faster.)
-You may be familiar with how they work: give a set of ```x```,```y```, and ```z``` values, and it plots individual data as filled pixels corresponding to a color map range you specify. Here's an example using the [NCAR Large Ensemble][lens-link]'s topography file (download it [here][topo-file-link]).
+You may be familiar with them: given a set of ```x```,```y```, and ```z``` values, ```pcolor``` and ```pcolormesh``` plot individual data as filled pixels corresponding to a color map range you specify. Here's an example using the [NCAR Large Ensemble][lens-link]'s topography file (download it [here][topo-file-link]).
-First import the necessary packages:
+First, import necessary Python packages and open the topography file:
```python
import xarray
@@ -17,8 +17,6 @@ import numpy as np
import matplotlib.pyplot as plt
```
-Then open up the topography file:
-
```python
topo_file = xarray.open_dataset('USGS-gtopo30_0.9x1.25_remap_c051027.nc')
```
@@ -81,7 +79,7 @@ Looks like the ```units``` attribute tells us this field is m2s-
topo_data = topo_file['PHIS'].values/9.81 # surf geopot. divided by gravity
```
-Also pull out the land fraction values and set everything ```<0.1``` (i.e., less than 10% land) to a ```np.nan``` (NaN value in Numpy):
+Also pull out the land fraction values and set everything ```<0.1``` (i.e., less than 10% land) to a ```np.nan``` (NaN value in Numpy). I do this kind of thing when I want to apply an ocean mask, for example:
```python
landfrac_data = topo_file['LANDFRAC'].values
@@ -167,7 +165,9 @@ I realize that this kind of thing isn't *that* bad, especially if you're looking
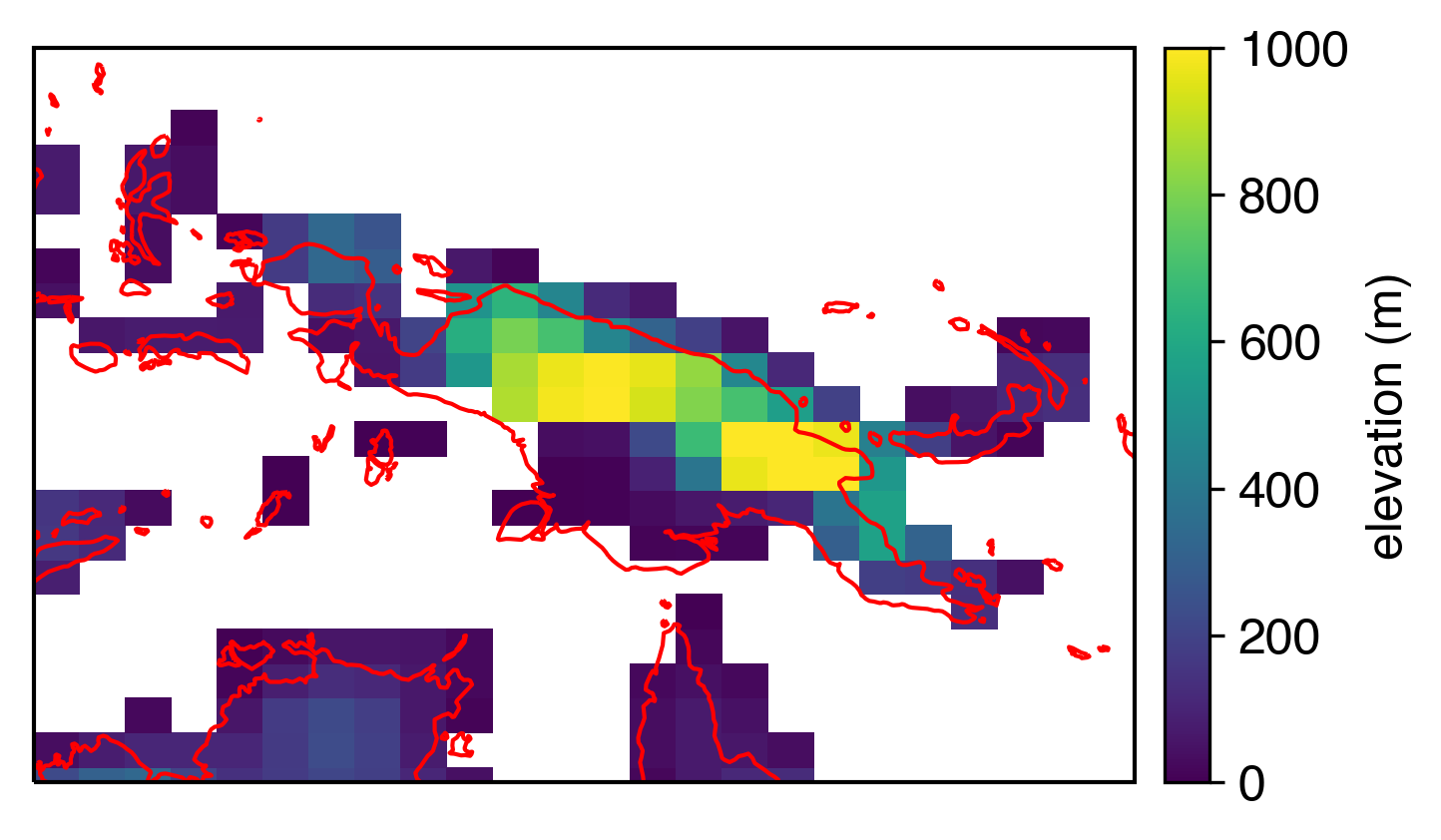
-What's going on can be found in the [```pcolor``` documentation][pcolor-site]: There's actually an *interpolation* happening, where the function interpolates the original grid to its **vertices** and thereby shortens the latitude and longitude data by a row and column each. So the elevation values plotted above are correct; there's no interpolation happening there (to my knowledge). It's just that the latitude and longitude grids have been interpolated internally. This leads to the offset seen above.
+Gross.
+
+So what's going on? That can be found in the [```pcolor``` documentation][pcolor-site]: There's actually an *interpolation* happening, where the function interpolates the original grid to its **vertices** and thereby shortens the latitude and longitude data by a row and column each. So the elevation values plotted above are correct; there's no interpolation happening there (to my knowledge). It's just that the latitude and longitude grids have been interpolated internally, leading to the offset seen relative to the map.
---
@@ -201,7 +201,7 @@ lat_extend[-1] = lat[-1]+np.diff(lat)[-1]
lat_pcolormesh_midpoints = lat_extend[:-1]+0.5*(np.diff(lat_extend))
```
-Note I use ```np.diff()``` to calculate the spacing between latitude and longitude points. If all of your values are equally spaced, you can just use the actual step value here. To be safer, I use the ```diff``` function, which would work better for an irregular grid.
+The above code isn't very complicated, and I imagine it can be simplified a lot more. For example, I use ```np.diff()``` to calculate the spacing between latitude and longitude points. If all of your values are equally spaced, you can just use the actual step value here (e.g., for a 2.5x2.5º grid, use 2.5 as the spacing). To be safer, though, I use the ```diff``` function, which I do in case the grid is not regularly spaced.
Now plug in the ```lon_pcolormesh_midpoints``` and ```lat_pcolormesh_midpoints``` arrays as your new ```x``` and ```y``` values. The size of each is one longer than the dimensions of the original ```topo_data```.
@@ -237,14 +237,44 @@ Now it's looking good...

-The coarseness of the model grid is still going to look a *little* funny against coastlines, but that's about as good as we can get at this resolution.
+The coarseness of the model grid is still going to look a *little* funny against coastlines, but that's about as good as we can get at this resolution (which is about 1x1º).
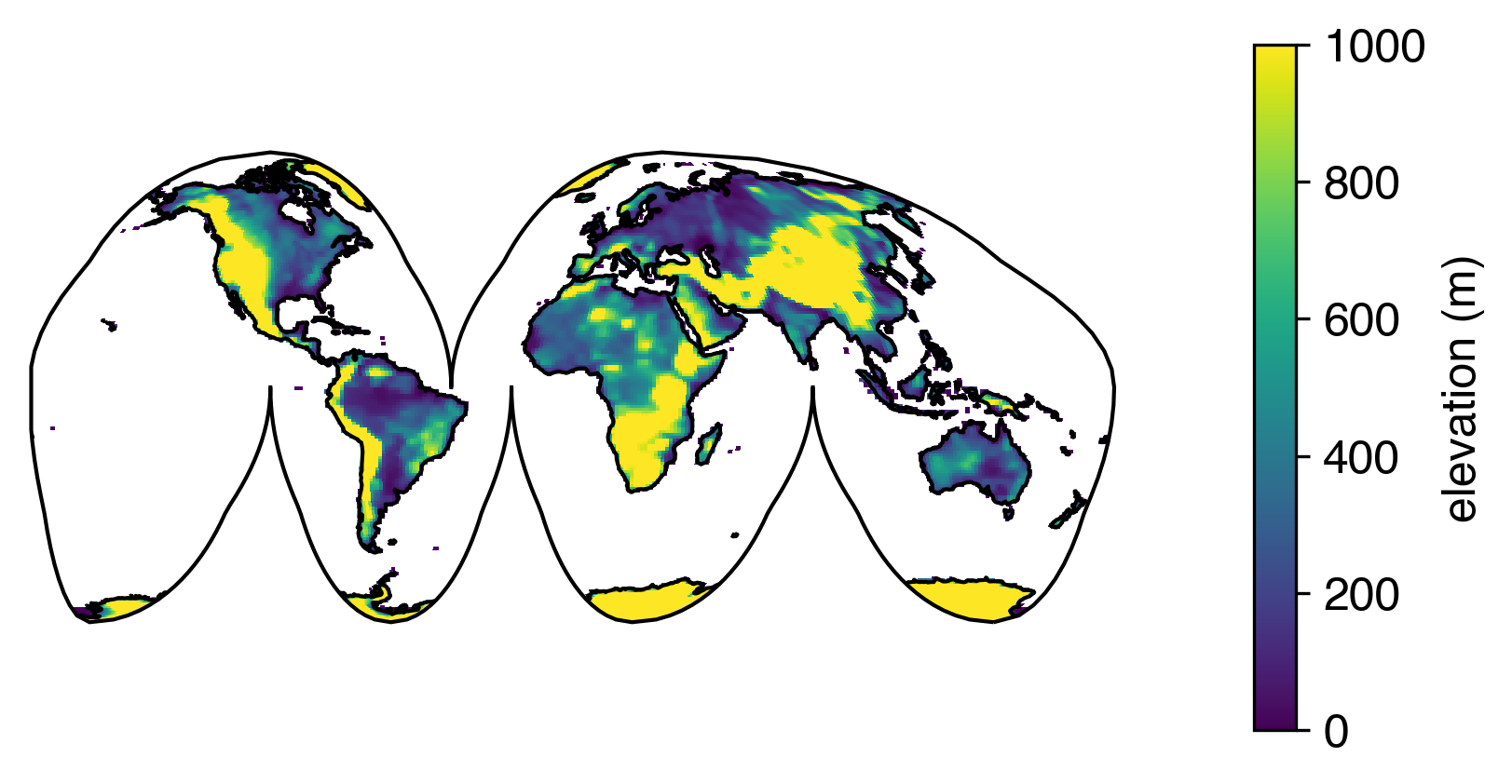
-Even on a global grid that requires reprojection, we can be rest assured that the coastlines are lining up as well as they can:
+Even on a global grid that requires reprojection, with this fix to ```pcolormesh```, we can be rest-assured that the coastlines are lining up as well as they can:
+---
+
+## What if latitude and longitude are two-dimensional arrays?
+
+This should be pretty easy—you'll just need to be a little fancier with the array subsetting when calculating the midpoints.
+
+Something like this should work (but I haven't tested it enough, so it's not once-size-fits-all):
+
+```python
+# extend longitude by 2
+lon_extend = np.zeros(lon.shape[0],lon.shape[1]+2)
+# fill in internal values
+lon_extend[:,1:-1] = lon # fill up with original values
+# fill in extra endpoints
+lon_extend[:,0] = lon[:,0]-np.diff(lon, axis=1)
+lon_extend[:,-1] = lon[:,-1]+np.diff(lon, axis=1)
+# calculate the midpoints
+lon_pcolormesh_midpoints = lon_extend[:,:-1]+0.5*(np.diff(lon_extend, axis=1))
+
+# extend latitude by 2
+lat_extend = np.zeros(lat.shape[0]+2,lat.shape[1])
+# fill in internal values
+lat_extend[1:-1,:] = lat
+# fill in extra endpoints
+lat_extend[0,:] = lat[0,:]-np.diff(lat, axis=0)
+lat_extend[-1,:] = lat[-1,:]+np.diff(lat, axis=0)
+# calculate the midpoints
+lat_pcolormesh_midpoints = lat_extend[:-1,:]+0.5*(np.diff(lat_extend, axis=0))
+```
+
[pcolor-site]: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.pcolor.html
[pcolormesh-site]: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.pcolormesh.html
[cartopy-site]: https://scitools.org.uk/cartopy/docs/latest/
[lens-link]: https://www.cesm.ucar.edu/projects/community-projects/LENS/
-[topo-file-link]: https://
+[topo-file-link]: https://bairdlangenbrunner.github.io/python-for-climate-scientists/nc-data/USGS-gtopo30_0.9x1.25_remap_c051027.nc
diff --git a/jupyter/.ipynb_checkpoints/fix_pcolormesh_offset_for_maps-checkpoint.ipynb b/jupyter/.ipynb_checkpoints/fix_pcolormesh_offset_for_maps-checkpoint.ipynb
index abfb267..fc8b1fb 100644
--- a/jupyter/.ipynb_checkpoints/fix_pcolormesh_offset_for_maps-checkpoint.ipynb
+++ b/jupyter/.ipynb_checkpoints/fix_pcolormesh_offset_for_maps-checkpoint.ipynb
@@ -5,8 +5,8 @@
"execution_count": 1,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T01:23:10.847236Z",
- "start_time": "2018-08-02T01:23:09.284837Z"
+ "end_time": "2018-08-02T03:29:33.746356Z",
+ "start_time": "2018-08-02T03:29:32.390963Z"
}
},
"outputs": [],
@@ -14,7 +14,6 @@
"import xarray\n",
"\n",
"import sys\n",
- "sys.path.insert(0, './cartopy/')\n",
"import cartopy\n",
"\n",
"import numpy as np\n",
@@ -38,8 +37,8 @@
"execution_count": 2,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T01:23:10.950094Z",
- "start_time": "2018-08-02T01:23:10.850608Z"
+ "end_time": "2018-08-02T03:29:34.709841Z",
+ "start_time": "2018-08-02T03:29:34.522699Z"
}
},
"outputs": [],
@@ -54,11 +53,11 @@
},
{
"cell_type": "code",
- "execution_count": 16,
+ "execution_count": 3,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T01:47:28.847165Z",
- "start_time": "2018-08-02T01:47:27.343763Z"
+ "end_time": "2018-08-02T03:29:36.079408Z",
+ "start_time": "2018-08-02T03:29:34.712792Z"
}
},
"outputs": [
@@ -98,11 +97,11 @@
},
{
"cell_type": "code",
- "execution_count": 20,
+ "execution_count": 4,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T01:48:02.789285Z",
- "start_time": "2018-08-02T01:48:02.185810Z"
+ "end_time": "2018-08-02T03:29:36.811807Z",
+ "start_time": "2018-08-02T03:29:36.094812Z"
}
},
"outputs": [
@@ -142,11 +141,11 @@
},
{
"cell_type": "code",
- "execution_count": 27,
+ "execution_count": 5,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T02:35:34.306803Z",
- "start_time": "2018-08-02T02:35:33.377692Z"
+ "end_time": "2018-08-02T03:29:37.817947Z",
+ "start_time": "2018-08-02T03:29:36.814822Z"
}
},
"outputs": [
@@ -186,11 +185,11 @@
},
{
"cell_type": "code",
- "execution_count": 28,
+ "execution_count": 6,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T03:08:24.136330Z",
- "start_time": "2018-08-02T03:08:24.107452Z"
+ "end_time": "2018-08-02T03:29:37.830586Z",
+ "start_time": "2018-08-02T03:29:37.822196Z"
}
},
"outputs": [],
@@ -214,11 +213,11 @@
},
{
"cell_type": "code",
- "execution_count": 24,
+ "execution_count": 7,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T02:34:56.382794Z",
- "start_time": "2018-08-02T02:34:54.420706Z"
+ "end_time": "2018-08-02T03:29:39.075319Z",
+ "start_time": "2018-08-02T03:29:37.833835Z"
}
},
"outputs": [
@@ -258,11 +257,11 @@
},
{
"cell_type": "code",
- "execution_count": 26,
+ "execution_count": 8,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T02:35:16.532107Z",
- "start_time": "2018-08-02T02:35:15.172629Z"
+ "end_time": "2018-08-02T03:29:40.455207Z",
+ "start_time": "2018-08-02T03:29:39.078480Z"
}
},
"outputs": [
@@ -309,11 +308,11 @@
},
{
"cell_type": "code",
- "execution_count": 15,
+ "execution_count": 9,
"metadata": {
"ExecuteTime": {
- "end_time": "2018-08-02T01:21:25.146596Z",
- "start_time": "2018-08-02T01:21:22.737334Z"
+ "end_time": "2018-08-02T03:29:43.537643Z",
+ "start_time": "2018-08-02T03:29:40.458512Z"
}
},
"outputs": [
@@ -352,13 +351,25 @@
},
{
"cell_type": "code",
- "execution_count": null,
+ "execution_count": 10,
"metadata": {
"ExecuteTime": {
- "start_time": "2018-08-02T03:18:26.151Z"
+ "end_time": "2018-08-02T03:52:51.898675Z",
+ "start_time": "2018-08-02T03:29:43.541001Z"
}
},
- "outputs": [],
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAADLCAYAAACbOm9uAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXecFdXd/99nyu33bl+WbbD0BRYBQRFBUMGOJRG7xhIffSzPk/wSU0x7UiRPTHvUJBqNidEIxk7sggo2pPell12W7fX2MjPn98csK4jI0myZ9+t1X7t35syZc+beO5/5fs/3fI+QUuLg4ODg4PBxKJ91AxwcHBwcPr84IuHg4ODgcEAckXBwcHBwOCCOSDg4ODg4HBBHJBwcHBwcDogjEg4ODg4OB8QRCQcHB4dPASHEO0KICd3/CyHE74QQXUKIeiHEzXuVqxBCvCuESAghFgshKvfad7UQok4IERZC3C+E0I51ux2RcHBwcDiGCCHOFEI8AEzaa/P1wDRgOHAm8AshxJjufY8CC4E+wNPAnO56hgD3ApcAg4Aq4LZj3X5HJBwcHByOLZMADYjute0q4G4p5W4p5VpsIbhUCFEOjAF+JqUMA78F+gshhgGXA89IKd+XUjYDvwcuO9aNd0TCwcHB4RgipfyRlPLrQNtem0cBK/d6vx7bOjgO2CClTHUfawEbu/cd6JhjiiMSDg4ODp8+IaBrr/eR7m0f3f5J+/ZsP6Yc80EPBwcHhy8aZ57ql23tZq/KLl+TWg8k99r0oJTywYMc1gl493rvAzo+Zvsn7duz/ZjiiISDg4PDR2htN1n8Wmmvyup9tyWllOMO8RQbgZHAlu73w4HVwCagUgihSCktIYQCDAXW7HUMHznmmOK4mxwcHBw+gkSSkWavXofJ48C3hRC5QogTgSuBp6SUW4HNwP8TQniBHwHrpJS7gSeAy4UQw4UQxd37Zh9xZw+CY0k4ODg4fAwW1rGs/iHsENYabDfSN6SUe6yKa4DHgJ8DS4GrAaSU64UQPwDewHY7PQj8/Vg2EkA460k4ODg47MuY41zyrVf69KpsTknd8sNwN31hcCwJBwcHh48gARPnARockXBwcHDYDwlk5DF1N31hcETCwcHB4WNwJMLGEQkHBweHjyClJO2M1wKOSDg4ODjsh8SxJPbgiISDg4PDR5AIMlJ81s34XOCIhIODg8PHYOKIBDgi4eDg4LAfdgisIxLgiISDg4PDftghsE7WInBEwsHBwWE/JALTSW0HOCLh4ODgsB+OJfEhjkg4ODg47IfAdEQCcETCwcHBYT8kkEH9rJvxucARCQcHB4ePIKVjSezBEQkHBweHj+BYEh/iiISDg4PDfjiWxB4ckXBwcHD4CHbuJkckwBEJBwcHh/2QCNLScTeBIxIODg4OH4vluJsARyQcHBwc9sNyLIkeHJFwcHBw+BicMQkbRyQ+ASGEBgSBTimdZao+DwghPIAf6JJSGp91exy+nEgpyDiWBOCIBEKILGAAMEAIMSAYDI7Qdb0ynU73U1U1X9d10zAMJSsrq03X9Xop5c5oNLolnU5vBd6UUm77jLvwpUIIEQImAcN9Pl+5x+PpL4QoNgyjKJVK5aiq6nG73ZlkMunyeDxJl8sV0XW9S1GUdillayaTaYrFYvWmabYB7R95tQEdjrg4HAwJTghsN/82IiGE6AdMd7lcQwKBwEgp5aBEIlHicrn00tLSxKBBg6isrPQOHjxYHzBgAAMGDKBfv354PB41FotRV1fXZ9euXX1qamrG7Nq1iw0bNsRff/11kZWV1WGa5nOxWOwZYIFjcRwaQggVuNblck3zeDwnulyu0tGjRycmTJjgLS0t1YuKiujbty97/ubk5KAoituyLLq6urxtbW3e9vb2wvb2dvZ+NTU1pZubm9MtLS1ma2srHR0dSjgc1uPxuNvtdqfcbndU07QecTEMoykejzcYhtGKLSabgDVSyvhne4UcPgvslekcSwK+5CIhhMgTQszMzs6+2e/3Dz3nnHPMqqoq38CBA8UeISgoKEAIoX9SPVMmfZvNtS8Taa+161VUpGX6AEKuPt5Euu1W4FZNdaHr2q2GYf5dShk79j384iKEGFMxpOhuXfNNyxhx0uk06XSaQq0f7733nq5pn/zVVBSFnJwcsrOzKSsr4/zcGwGQ6TSvZ54AcHW/OLv0vyiykvx1/Q8pLS0lHA572tvbPe3t7fnt7e0D29vbaWtro729nZaWlnR9fX167dq11o4dO3zZ2dlNqqqu6OzsfM+yrBXAKilly7G9Og6fB5xU4Tbiy/bgK4TwATNycnJuisfjE88880zjhhtu8J911lm4XK5e1REOhwkGg4zXTsMoyWH1rud69g0cE0S/6kI2fuuxnm05088iumUtRWoLQwcorF2dwTCU77S1Z+6RUqaPdh+/qAghFOD8cWM8Tza1ZHRj0omooeOpe/C+njIKKsl0Al23dXtM/rlszawmGt4NgFvxM1mezTzrqT112uXcp1GgliDTaYSq8lrycaYrM+06vV62KOvZEV0BQL6rnHy9jBdWPcLAgQN76vgo6XSajRs3snLlSpYvX55etGhRorq62iOESHg8nrWRSOS9dDq9DFgF7JBSWsfgsjl8BpSNzJL//dSEXpW9Y/jry6WU445xkz4zvjQiIYToFwqFfp5KpS4eP368ceONNwYvuugigsFgr46vrq7mvKpLSFlx6tlBDoV00LxfOT3XT6Z9XyPh/ZfKOHGsp+f9qnUp7pzVyuZtGVlTl5lhmvKlI+vdFxshhBCCSwZV6HOygor41i05XHS2n1veLeXxb21Da0+Q4ytj8+738Xq9+xyrq14MK9nzvp+7ip3JNT3vd+7cyfr16zn77LNRlA+f/EzTpKamhoqKCoQQdHZ2MnnATLZGl5DMhHvK5bpKyff1Y/6aOeTk5BAIBD6xL1JKampqWLVqFStWrLAWLVoUXblypRqJRNRAILA5Fou9mEqlXgYWO2MfX1xKR2bJ/3pyYq/KfnfEq58oEkKIO4D/BrKBZcDN2O7M3wI3ADHgZ1LKB7rLVwCPAccDa4BrpZQbDr83R8YXXiSEEH0CgcBPLcu65vbbb9e+8Y1v6EVFRYdUx4nadJaY8/fb7hY+Up/gku6bO4qGdvuGdcIYN30KNb56boDLLwqiaYJ5C2Pc8t0WcnPca5atik77d3RTCCEmjR7pmacI6fnlD/M5fbItAud9p5NX/9FKRfEUttW9dcCn+eFDvsKGLc8xOG8yLeHNtKcaDlgWYOvWrUwadz5NXfZv6rjgNFaF5+1TZnr+DazpmEeztWvftqLgVYP0UcvZEl+Jqn7okz5Dv4xd1jY2WsvIoQAPXiZcdDwXX3wxX/nKV4jFYqxYsYJ58+YZzz33XLyurk7zer3vdHZ2PiOlfE1KWXtYF9DhM6F0ZJa89cmTe1X2zhGvHFAkhBAnAs8DE4F64GfAeOBxbOE4G8gF3gKmSylXCiHeAd4GfgXcBFwppRx9ZD06fL6wIiGEyPH5fN+XUt52/fXXqz/60Y9cffr0OeR6yvwjaIhvRqBg8KFnSEUnJHLpkq1YmPsd5/JkUzFwGm+/+Ucm3vwzpFslFeugrP4p2jtN/vDLQk6f7CMet/jx3W38c26U+kZjqpRy4RF1/AuCECJ7dFXw+da2xJS7vp/HFV8JYlmw4P0E51zXgkxKRo+/ieUf3Hfwyg4BRVGR0kJXvAzzTaDIVcFLjQ8Qi8XIyspiSmgmi6L/wiBD/+zx9NUryMrqhxnyYgR0Uhureb95DnnuMqx0ilzRB5/lp4bNhEQ2DbIWk30NhHKGUCM37bOtsbGR119/nblz58Zef/11VVGUVsMw5sbj8ReAt6WUiaPacYejSsmIbHnTP0/pVdmfVL3wSSIxDvgXMAWoBe4C+gN5wMNSyn90l7sP26L4E1AN5EkpU90u2nZggpRy4xF16jD5womEEELTdf1uTdP+Y+bMmerPf/5zT3l5ec/+WCxGNBqlN4IxxDeeLYlleLQQSSN80PKKcGHJNKrHj5m0XU6BvP4UVU5m3fyHcLvddr1Trye++THOP9PPj7+VS2G+xmtvxbjuv5vICnl+t3lb7Ntf5igoVRXnFhVqL55/pp9f/iCPUFClelOKqqn2w3RR4WjWrHudgoKCQ647Fovh9/s/dt90zxXMT80B4LihV7Jq4z8A6C+GUcOm/cpPq7gdkZ+PsCyUcAKEQHp0wvF6Opo2sTWyhCJRTqdoJ2p1AOAnhIlBf1FJk9y1j0syizzceMkWBTyz5lGGDx+OoiiYpsmKFSt49dVXrWeffTZaXV3tCQQCyzs7Ox+3LOvJf0cL8/NO8Yhs+R//nNKrsj+t+tfB3E0PYFsEAAlgNLAIOEVKub67zM3ANODvwI+llOP3Ov4D4BdSyhcPpy9HyhdKJIQQg4IiZ0tEdjBCOZF15gcAbNiwgbNOuY721k0kiPY86eWNmIgeysHvzmfF3HsxDIOtW7dy1Sn/SZfVRsZK0WE2oggNq9t9PHbAFYTbd9AWrSFphBGKQtyKdLfAvlaF/U4gI1NYITeiPUI63okRi1Co92P1rrfJzc1l48aNVFZWAlBRrrHyjX50hU0uurYBw3K9vWZ9ZPqXbVBbCOEaNTw4u7Mr8dVH7u3DlIk+DEPi678Vs9sY27hxI0OHDu11nZlMhuGTryXcsp3WHUuxpF3RhKwLWdT53H5l80JlRJJNAJzkOoe0TFFnbCFNkg754Q292DuUUVmn2288blBVMOzvgMwKkCoKoEUzaDXNIIQtINkBJNC+bRk16WpajA/dVSoaY8RkksRpk0100kqaJBYWKhpZ5NJX9OfxVX/m6+PuoNnVTGNsEykSZCkFdFkt/wE8KqVMHdpVdzgW9B2RI6+fc2qvys467rkaoHWvTQ9KKR8EEEKcDswGzgK2AHdju5tGAxVSyrruclcCX8MWieuklNP2VCaEmAf8TUo5+0j7dTh8IURCCCGKTzrfavrgFQZqo1jevoBAIEB/7yjaRQvJVCflhSeS5+tH0AhgCINWTycdeSmMjnaSnY3EG2tBStx48KpBDDJ0ms24XSGMTAJTZgAIuAtIpDuR0vpYN9NercKt+UkZURSvl75TLqLhtSexpMHYad9h+bxfcfqQb/DWtj8gLZPbbsjinl8UEo1ZXPGfjexuoGHVutigL0scvhCiuKrSu7l/ueL/2R25bN1psGV7mr/NM9iytAuAFStWMGbMmF7Vd1boOrq8cVbyLm7pIbtoGH3yqwi0S95afTcqOi7VS1/3IIo9g9neuYQiyvEIP5usFSREnLSV3MeFuDcn+y8i4MpD+LyYZQXUnhEglW+hhxVcnRBokET7CiwdArslWVviCMPC9GkISxKu8NI+2CSwxaBws0EmaEfOeba3IptbET4vmUwConEMK0Ob2UCD3EnMl0ZNmMRkV09b3GqAtEwgVBV/bu5zkabG/wWWfpmtzc87fUfkyK/NOb1XZX913DOf5G66D0hJKb/d/T4EdAEGMFxKuaV7+43YlsSjwJ1SypP3quM9bEvilSPo0mHzuRcJIURJoHxInVnfTMLopEIbyaDQBMJqF4tbnqJgwAn0OfMi4gNcGDkGqtcglJUgx2vfe3d/UErWFolvwSY0U0XPyiFTECCVrRMrUhEmZL27iwXVv9/nvAV6OZ1GE5nuBzuvO5eR/S+getvzxIwOKnJPZEf7Yvorley0NoBQKDvnKjpWvEe0YRv5+ZWUlk1i5YoHKR44iXZtN/GFdlinaUqu/0YTa6rN1jXV8QopZfTTvapHFyHE2JK+2rJzp/lEImnx8vw4Vcfr1OUMxlsYIPfJwUSq+sDOevJDg3ht5U8PWmeVdxIblTVkXX4uwRHj8DUqZO2w0FIWnuYku3YvwsjEiXTU0pTasc+xuUoRpjApcJWDplE+8hw6ti2ntm0pg5Xj+CDzKn6RzaSsryI0DbweEiOK2TETfj9lDkElyY1vX0tolQupgOkGNQWeDokelSimxBU20LrSbLrJw52TXmLWu+eSvVYnPD6JL5DC/2yIYG0KvTWKSBnQ0QVuF2gqeD10jcqnaWAClu0gMLiSRF+VqNJI4p3VRJctR6iC4MhxtL/xSj9n0PvTp2hErrxq9vRelf3t6Cc/SSR+Bah7iYQPCAMrgVlSyue6t/8eaAGeBJYA+VJKq3tMohk4Tkq5+wi7dVh8rkVCCHEu8CJAv9wTqGlfsl+ZASddjvu08aSyJabX7ou73Q6FzAxMMKNyLZsjhWxf2B9vM+gxiZqSIASWCpYGmYAg0x0p66lN4WuXeCISrSOOyJikSJKq7IvlVvFt6WThyrsxrTQVuRN47YNHOXnYabRYdYw//jZ2erfQ8u5rABS4+tGc2klrayulg4Zz0WkJHvxNH/w+BcuS3HxHM6++K3fvro0MklIm9+vcFwBFEeepqnhB1UDm5pA9tYrNf5pLMBjcJzpICBUpTU6r+h5vrPnlAeuTUjJg1Ax273yPkfd8lVh2Ofx4DZvXP0Pf/OMYePKVeGsjLFzzO9LmvqHIee4yBhRPIc/KB10HXSPePxstbiAsid7QhdXUwluROZS7Khmoj0LoOsKlg9tNfGQxLaN1EsUWWRWdpDMqyZoQwgAkaAmBsECLQaBe4oqYeOvjxEv9fOe3j1KidXLdmq/h1kxuqHiPG7Ma+GbD8YQNDws+GMng2bY1Ei/1Ey9QSeRDbFCGnD4RIlEP/sU+tDikgpJYUw1d65YSXb+abLUPrYkdp0sp3zxWn6PDvvQZniuvmH1Gr8r+35h/fpJITAaeAs4BNgA/BYZj39euBmYAg4EXgJOllFu6xyCeBv4IfAc4VUo59Yg6dAR8bkVC07QrVOl6PM9XQUO0GhAMCI7Dl/GwLvlOT7nTptyFEdSJ9VGRQpAOQWSgiacozj1jnmCw3sHSZCmDXU38avc5rH1hKNnbLPS4heEWpIMKkXKB4bPr06O2e8HXYuJqS6EkMqBAqsBHQkmwedFjhLtqenzjeyNQqDjufLavfh6Afn1PZmf9uwBEo1GKpp7CCZ6N/P2+Ikr6aliWxDO4Fl1zbUuGo8O+aHH1mku/RPe5H++fN00rzB3GwqX/27NvStZlvB3+JwD+44eQXF9Hvrucuta1HGg29aZNmzhp2sWkwq2U/f4y0u2laC+sY8vbjwAwsP90yoacjpo0Sa1ZzbudTwLgVYNMybsSFAWrpACkRInYmhurzCdeoJK/uA12N4MiwJL2X4CMAYqCcLvA5SIxopjWkTrpLEiXpZGmQImrSAFCYv+1wNugEKiXeNvs74kwLOqmBVn3X/ez24zwfqKUMr2NCe59+7ogKfj+j25CTUtifRQsFyQKoWxcHaX+Lj6o7U/OSz6yN8UQSQMZifDW9j9hyBQuzZNIG8kfA79zJu4dWwqH58lL/3FWr8r+4fjZBxu4vg74AVAALARuxB7DuBe4BugEvrtnzEEIMQR7nsQoYClwtZSy5vB7c2R87kRCCCF8Pt9P/H7/HfPnz/eNGjWK8ep0llnzyaGAGBE8epCs/MH0K5mI1a8PzeNUJp2+hv9XNI9sxWRVqoCV8f4M8jQx3VdHnrJvNEzV//0nroj9Y3eFLaQqiJQJlAyoaXB3StydJkpa4upKo7VEyHS08E7bHILkUKCVsSOzjhRxvPjxq9n2QLYCUdmFNDM959r7+hqGwcARZxNreZPf/rSAq2eGCF2QRWrDBrwoD4fD4a9/ahf6CNE07dJAIPC3BQsWeEeP3j+E+wz/NdQMTBKVHfiULHILh7J43l0fW1cmk6G44gTCTVsorJyEcvskvHV+EnPfoHnd2yTNCCdUXE127gBMvwukbeUlI21YRgo/QfC4sbL9WN03ZZGxkLpCJqhj+FWCy3dDLGEPUrtdtlBIyxYJTQVNsweopcQozKLxJD+m17Y0pWJ/V9QUqEn7f4QtGJ52SbA2BQKEKREZi0xIp3OQi/AQC9NnMXxIHS8N2ded/E4SbnjqZtztAn1SO1X5DbSm/GzYkY/5bhPtz84FRTDoglvIalFh7RY27n6dlrR9r1AU5TbLsv7iDHQfGwqH58mL/3F2r8ref/zjzozrTwshhCsYDD5SWlp6wfz5833FxcUANDQ0cHLxdHawnhMC55E99HiSff3svAAmtj3KE99bR86gHGaMNbjxqiwG9NMpKjxw7p/K96/C/3oQT7uFtyVt3xh8Gl0DddIhUBPgDsseEQlu6GDzpn+RIsFuYysAyWSSOXPm8Jvr/0Sju5GwbKf/oOk07FpKOtpOtlpAGYPRhc4H6Vf3Of+6deu4cMZYCvNVcrIVXp4fJxgqsNKp8O3JZPJPx+4KHx1UVb0gEAjMeeedd7yjRo06rDr2pMyYZz3F2NFfZ0PXC6yZL/ht53Ree380/V8wWPbW3VQExrC28w1OqLiaWLQJmU5TGhiBortsYQh4wLAQ3eFTUrddXNJlf/6JIi+WJvC0pnHVdUAy1RPFhLTdjigK6Bq43UivC6kpSF0lWu6jc7CC6QIlA0r3YcIEPdYtICq4whJvm4WlQjLHPr+WlOgxC8WQWJrA9Aiu/smL3Jz1oVu52YxSnQnyVmQ4O+N5vLNpEPr/LmLrhn/1lPHll9Hnnv+ANzqJzH6a1mQNA0LjKR3tjS5btswwTfM3qVTqj1LKzsP6IBw+loLhefKrj53Tq7J/HvePL7VIfG4yWAkhtGAwOPfEE0+8cOnSpT0CATCt9AJ2sB6AJdEX2dS2kDZ/F21/epAnvrcOgGhzgg9Ef279XjMjp9Rw07ebMM2PF0B1WRDTDaZHkMx3kc7WMb0KahKQIDVIhwQZn0AqAlRBl9JOUIZ66vB4PFx33XWsl0sZnh6NmUlS1P9EThp0PQO8o0nJBO3ZcRZnXmNk4Zn7nH/kyJGs2xCmqfhrrO07Bl33U1ZxhqLr+m+6Z2h+bhFCTPb5fLPffPPNwxKIcDjMiaHzsfbyloS7dnHp9Bj/Nbsfz/x0E/5dClpjJ1jQ2VlDH3cFS3Y8xvqW16nuWkAk1gCmhdRtF6PUVaRbtwVCUZBq93ZFoKQsLA2E1S0ImgqWtaczHzbMMCGdRsRt15HImPjrEuhRWxQsl/1XS9iWRSqruwoLkjmCtkqVaKmKkBLTA7G+gq4BKpEyDcW0x8H+ftcMhj38nz2nLFQDiHVdPPy9rSz83hs0f3cW22s/nPk/bMAMiMapvfrn7Pjrb2kzbIHxnnAiCxcuDCxatCj7ggsu+IHX693ldru/KYToXXIyh14gMKTaq9eXnc+FJSGEUILB4JPjxo07+5VXXvHtmZT2UfoGK2mMbtzrOJVhBafxz/m/paqqqmf7kDv/l8ZX/kxk1U6mT/Hx6hMlPft+0jKCORuOx0joqC06whJ4WuzIlVRIYATsm4CaBC0J7g5J9oYoDctfYaO1gsFKFW83vUp+fn5Pnaco57NUXUhpyUmUDjkVvaGLzVtfpC6zmX5V51C/5R3yy46jtnreJ6aUeP7557nqqqtaYrHYUCllx5Fc02OBEGKoz+db8vzzz4emT+9d5MfenF5xK2/tvB+JpCIwlu2R5QCUTbucujee6Cl32ujvs6v2XZo6qxklT2IjK2iV9Yz3nYXXlY1Py0IW5iF9LvuGryhIVexpJFIRWLrS4z6K93WjZCShVU2QzkCq20PjcoGq2K4mgFTaPsbjRnps0bHcOm2j/KRDtiWhdc+TTuZBxm9vM92QycswemgtE3K389DqSZhxjVBBjPxAlJArRX0kROfqAoQB6ZIMeUVdtG3PxXXnM7SldvHnf/ye1tZWHvrVQupbVkAyzUjXRDaHdlDbtIi8wADMeJRirYK1iff3yVO1bt06brvtttjy5cu74vH4rZZlzXXCZ4+M/Mp8OePRGb0q+8gJj3ypLYnPPFW4EEIEAoG/VlZWnv3iiy9+rEA0NzczadhX9hEIgKCWx/Kdc/dLCrd51veY/maapq+mWPTqL6nZlaFfmR1++tOC9XzQ1p/maIBwJBslBels+8ZiesHw2a4FLYZtVShg+nVKQiMwwhnqrZ30LSimWFTwbs18ysrKcOPmRM/ZvF37NIVDT0aWZjNUu4iioQE6h2pUrRjF6jfvYUjBZDY1v73PD3xvLrzwQq699tqsxx577DHgvKNygY8SQohsv9//5j333BM8HIEA2NaxGE31kDETeLUPrbKR63OJaIV0GfZkt81182jqXMdx8iTq2UGnbCGo5pGbOwQhJegalt/+ngiw3U0G9j5Aagoio2D67c9cTUssVZAYXIB3S/fk5vRe8yeEQLp0cLsQlgWpDCIJSInQVXI2JTHdCokCHdMFlibQo7ZIZAISJSNQvQYlvk4GuZvYeuojJGSKOZFyalL5VLhbqCqvo32Yj782nkJzws+OTX3J6tdJ12kjSK9s5+KLLwbg5ptv3ueaTcm/kloW4RszlpxGlR31b6OqKvF4vOd7P3LkSBYsWOB/9dVX/bfccss/2traNgghbpJSrjisD8oBicCwvvxWQm/4TC0JIYTw+/33DBgw4Ib33nvP99GMrbt27WLvlBsAY/NmsKxlLoZh9KSTPhDTym9hUdar3D61k1k/+PDJ/4W4j++vuZBMRiMUSNDR4ccyVJR2HS0qEBI8rbY14W238LSm0aJplNYukJJ0vJPN7e/RaO4EYAAjaBUNZDww4No7MPy2CAgTUvkgDMj9x3o27n6NdDJMkVbB5vjyfUJE95BIJKisrIzV1dV93TCMJ/Yr8BkghFBCodD8K6+8cuKf/vSnjzfzPoGT3eezWVlDa/LDAI3j885nWevcvc+xzzF+kUVIyaPZ3MXQ3EmUZ43FyvEjVRXLq2F6VIQhUZMGSjxj39z3bTRSU0BKzICb9kovlgaFy6Mo4Q+jjYXRHaWmCKSigCp63FCm302szIvpEsQLBQhQ0oBiC4TpgXRFkn592+jjizKn4uMjVB/q6otPSVGkddFf72KgZmeanbH5LFa9qNHyx4cpG38B8//2U4LBIHV1dewdDLBx40aqTpmMe2gZhSeex47f/hyPnsXEzOkowv6u7UmdbhgGDz/8sPzud7+blFK+GA6H/99czuU4AAAgAElEQVSeWb0OvSevskCe9ciFvSo7e8JfvtSWxGcqEl6v91slJSU/W7JkiS83N7dn+5neq0ERdBhNbMgsodw3kpLAcF5v/PMh1b/nxlNYoFC/esA+N6JV6SS/2n0O0YyL7W15GIZKptWD3qmiGOCvBy0hcYUt9KiJkjbRYhlExkTEU8iWNoxUgrrUBpqsOsK0M3DQ2eRMOJVImSBZKJGaBAmuDgV3BxQ/vZOujh1sTC4Bl87mmhUfm79o6dKlTJkyJZJIJAZIKVv3K/Ap4/P5fjJixIg73n//ff/BhPmjnOK5iEWpl/Hp2cSMdkxpUOQdhCkNdoc3M8I1jibs67c3fX1DIZUmy9OXsvLJKLqOGXDb1p2uYHpsgRWGRO9MIEyJVAVSVRGWhUgb9tiERyNW4iVaomLp4GmT5K7pnu0shP15ZkwwrZ6wWMvjAk3B0lVipV4SBQrxou45NXkGeWX2GHHbrmwwBa6CBMcV1+PT0vyt/B0+SkKmuLPRTjudsjTGBGqZ6tuCiWBtNJ/bby0jvWQ1XbF97+VtbW3s+V1Eo1EGjT+H1oZVBE+fTOezLzOq7EIK62xnwB6R2EM4HGbWrFmZe++9N2MYxnczmcyfnLDZ3pNbWSCn//WrvSr75MQ/OyJxTE4sxJRQKPTK6tWrvTcO/C4A88x/cqbnSuh+Onot8dgnVXFQFKHi1bKIGx08+oc+XPnV0H5lvtlwPJsjhdR25JBM6pidbpSkQnC7sKNW2k0sTWB4FaQAxZR4Wg1cbXFE0sCsreX96Fzcmh/F56ffJbfSNRh79nfQDoU1wzpal0qgRhDcbaK2xVj9wZ/xu3Opi6z72LbffvvtqUcfffS5rq6uy4/oIhwhQogJwWDwzerqam9paekhH1+gldJq7kYTbgyZorJwGjm+Mt7f+TdKGECUTsqUIWR5i/ATQkqJFfKg+7PssQZdQ/pc3QKgIEwLhMAI6HZQAaAmTZSUgenRsFwqStpE77SthXSeD9Oj0DjBFrfsLRJvcwYtYZLO0rF0gRYzcTfFUZK2C0pqCpk8P4ZPI1asESkXnHP+YrK0BHXJHB4sfX+fPl609QzKfR1kpEKlv4Hbsz+cID0vobEoNpgtsUK2d+XR3BEksMiHHpFkggLrtE4UxSK5JIe+LzWjdMZYs/MZ2qwGwF7nZE8OMICq029n07onyTTbrrkzqn7Aa2t+ccDrv3HjRi655JJYTU3NmnA4fJkze7t35A4rlKf3UiSePvmBL7VIfCbRTUKIUp/P9/xTTz3l7d+//z77Xks+zmuJx45YIABOdX2V48QE9MJs7v5DBztq98/j8+M+71CVVU+OP46um0hVYrksIgMtIv26B0FVO9IpmSNI5iikszTS+T7QVbS8fEZrp2DINDmhCqRmu6lwW1imQEqQIkzXuuU07lpMc3oH1VufJWw0szu6nkwms3/DgVmzZrl1XT9fCDHpiC/EYSKECPj9/uf+/ve/H5ZAnBn4GjmeEkq9I9hjw+3qXMWq3c8jEHTRxnHuKZQMOw3/4FEowQBqKIjuCdgC4daQLs0elLZAiWdQEvZLZKw9+RZ7UFMmQkq0rhQilUGkDfT2BGrSIlAL7g7I+ASWu9sSERArUukc5CI6KES6b8iOkBICYUmEBNPVbV1IwY/zN+wnEADPDXqde4qXEtDSbIj15aloVs++TtOPT0mjCYv+oXbOH7qWwgtrkarA12zheS6L4lCYUWdtYcctuSTH9WfMibdQ4B8IwPDhw6n0T8TqdqetfeM+wjU1lA6wM5TuyTl2IIYNG8aKFSv8d9xxx3iv11ut6/oN4pOiJxwA+6tlSKVXry87n7olIYRwB4PBpd/5zncqf/jDHx7zgfNwOExWlv2j9fsE775Qxqjh+7rVn4/5WZMoJ2p6WNZaRlM4SDLmQq/1ENom0ROSVEghlW2XVwxwdUH21iRaZxJhWVg+F6lcN4kCjWixwHJBKt9CNMWp+/WvyKQ+TCFR5BpAS2ZXzw98kHYcWzKr9mv7448/zi233LIhHA6P/CxcBaFQ6IFzzz33mjlz5ngPXvrAdHR0kJubh08EiMsIKhoD+kymZOR04sVuTB3iRQLDC97ucWWp2pPV/E0Sd5cJlkRqAndLCjWetkNcPZptTUhQ0oY90JwxEdEkVnOL/d7rQWRn0Tm+iIxP2J9dxMLTZj8wtBznRar2+EKsvwkuC/9mHX+DxPAKuqYk2DL1kUPq70txD+f6Phz3+FqNvS6BIRXSlkaxp4vXXxpHcKf93ZICIpdEUBWL+IYccjZKMqrJjtf/RqR2ExL7o29qaqKwsLCn3unuy1CEvVRrb1izZg0zZ86MNTY2LgmHw1dKKRsOqWP/RmQPK5RT/nJJr8r+a/IfHUviaBIMBv8wadKkgXfeeeenElkVCoU4eepPUENZxOKS7/1ifxd/UElS7mpDEyYF3hhCSBRNYnjtG4XpEj2zbqViv7SUJFbiJjIkRHhoNtEyH5mASirbfkgTJngbFRoefJBMKkZxgZ39tEwdytvrXsWUGSryTiIgstlqrKZK3X893csvv5zy8vIyIcSn7nISQkxUVfWaP/7xj0ckEACXFt0KSJIkKNDKmFJ4Df37T8UIaKQDgnSWINHXIl2SoWukQTKve1azBFOHSLFGrK9mX39NIIXoGXcQlkSaGcxkAiWeRrSHkZ1dWIkkVjKFjCUgFkdLWOgJiZqRuLoMlISBFKDHJabbPpeanaJ/eTOF0+sInx+lc6jE7HRRa0QO0sN92VsgAM7LW40hFZoTASwpCBsexp1RTSpLkPbb4buBZ0IYi3LwNkEyV5Duo1Ex7Wu4sj8MuFiyZN/cZfNST/RaIABGjRrF2rVr/bfeeuskr9e7WVXV8w+pY/9mWFL06vVl51MVCSHEVF3Xr5w9e7bvQGGgx4J33/ofSvucAIB7oJ+nolk8Ec3p2X+61+TaUDPl7jYGBloYnN9KXnYUK2CSzrYnSxm+7vQMstuSCJuoKTv/TqxYIRMQpAMC0wUo4GkHpa6LZHMdA6suZNjA83EpPnaZm5hUOR2flkPCihLtnihba23Zr92KonDfffcF/H7/b4QQhzZifAR0T2x89IEHHvDuHVBwuLyems1w7URUoTGy8Eys0UNIFHlpmKihn9/C49/8LY+edz8XjF5JYVkH3mbI2m7gb5YYPkHH5CRtoyWYEiVjsa1hARu3v0C4tpq162fzxpKfsXjzXyGVsfM3RWMgLdqsBj5IvsTCxkeJLpiPvy6Jvy6JqzmC2tCGq76rZ1xDamB2uEkaOomMC783Rc7QNk49fj3z44Nos2IH6eWBmRno4ht955GxVLZ35FLubafE00myEHLXx9CjFhm/wNsKpa+0UDq3AcMLyXNTBEeNIes4+7s7Y8YMSrSBR/RZuFwuZs2apb/55puB7OzsJ/x+/08d99P+SITjburmU+uhHe3qn/3II494s7OzP63T9pDJxMm+6FzWT/8v/m/76VwW2H+u2mBXI5XeesZk72J0/m5wmz25eyy1e/5EAvsJ162gpizcXRI1BVb3ZC5XBLxN4Gm38IgglTf8hJJ+E2lr3EDastOXN5s1xI0OhiQG09raygTtbCq18fu1B2Dq1KmMGjUqoKrqtcfo0uyHy+W6deTIkUWXXNI7c7s3rM98gJ8QnW3baRvuonOARvHx9Xww+mlG6D6GJyX3jn2CpWf/ktz3mvCvayJnYQ3xPtCnIIzWJ4HpUahd/yo7mt6nJrqaD1qfpjFiz50ZGZhiRycpAmmaNMgaVvEuuRSSIEpdZC16bStaWxyRNu0wV8sie2uS3E0mgTqJGldo3JFH/NVC0vPzCa/O563qYayPl/Tk/5qw6mIWJA/9njrerbNgxFy+PXQePjXFZTmLGTd1A8Ky8O+I4G8wcEUsOsbmIz06/V6Okd4VQD9tGKkdOxn7lf8BoNGsoampiTM9V3KGflnP61CZMGECa9eu9Q4cOPDbwWDwX0KIj1/u798V6VgSe/jUJtMFAoG7zzrrrOwZM3o3i/Fo09W8hXuvUbh2wuYDljndawKtEGzlno7+vJYeSTpHYvjBv1ugJuwnTku1BzSVjEBNSwL1aUyPilRAjxhYukKkTCfjF4SafOx+/zm2tS/qOU++UsyzC55g8uTJACzKvPyJbf/Vr34VOPvss38mhPirlB+TfvYoIoTI8Xq9v3jooYf8R/KAGYlEGD/2aoTfiz+uIaUkanWQbeYSOaOZQNsubnK/x6hbNbbPj1ChVALbAViatZDyMy4hWGfhaYfU3EL6rU+g1O1mU+R93nrrLRYtWsSdd96JJlwYMs2S1CuUfOMmCleWUfBikvbmxRRRTgu2231o6ZnIoM8eEK9vsteRcOnoTVHSWTkoBuRUQzJXxfBDOmRHqG0/8+F9+vXA8H+wNlVqT6TpJQmZwivscbArg+1AO+8lXdRGcggYFqgCb32CtuOCRPpDvDCf0E4TrcWgYIlKp4Tlz/yEicWbWNQwh6KiIgBGaCdSog48JJfT3hQXF7NkyRLf9ddfP+3FF19cKYSY/llmG/08IQHD+vJbCb3hU7kKQogJqqped//99x+xf/twWLJkCYZicvX4QK+PuTi0FtWfwdK6Z/F2XyklbafrUNPSjoDpHk6WAkyXguHXMLwKliYQJnQ2bWZ7+2JO9lzAMO8EhnlPosXc3SMQvWHSpEkMHjw4IIToXUzeEeD3+398ySWXaCNGjDiieor6DqKxeSVtzdVsb3iHHXULGVpwKvU/nMj6H/2Lt2+by5VnNrFtvSAT7aTD1UVh/kiys/qTWLmemncfo35snES+fcPO+DVqw6vJV0qYOnUq3/nOd9i4cSO7G3dxRsU38OWV0vyj+8ma/AH1lw6hrPJM2rQ2Plj7HrrwUBNeSVo17cFsv8+2OgwDdBVPSwp3l0mkXBAdnqZkWi1jJm3mp1Of269fo10erg4e2tSVPQKxNyd7FB6pfIyOESGEYX+JMkEwApLwQIt4nsKOu/+HNfN+h5Zrj0tkZfYN4V5vLEZyZE+yHo+Hxx9/3POTn/xkgM/nWy2EOOWIKvySIOmdFeFYEkcBIUSu3+9/9qGHHvLune/o06S5uZkp4xKoau/96yVqkLOGVvPa5uGIiBdTB0W3J9hpKdDjlj1vwpA9s38tP3T107BctqjElixjxzv2srTtyTo2yGWH3Ydf/OIXgcsuu+xuIcSzx2rdCSFEpc/nu+muu+7yHEk9UkqSiQ5uXXg6Qwqj/HnbuUSTbtKROM3PvExy/TY6m5q5dOj3eXv7HAwrRWtmF95gIeHanSAUMvXNDFr/F4bcegovvlpOSrQRN9totXZTPHMCbS9tQkFgZJIMndGXuydE+cb9uUxe/wY/vnMV8vuS4beVMmXqxYwLnc2izudoCG/gtLKbUQG8HqTfh5HlIePX7NThAraf9fBBevchj4QL8SspZga6Dl74YxioBWg+yUKPZ+FaW4u1K4k5MpuKfs3sbLSX1R2bey65aTv8+JWWB6gMrGVjzA7DHa6d+Im5wHqLEIJvfetbalVVVdbMmTNfDQQCf4rFYj/8oi6EdbQwvwTjDUKIImAiUAxYQBPwwaGscndMr4IQQguFQnOvv/76vJkzZx7LU30iV//m9wwbdOgJMt2KgaqZthspBq6IxNNp4WtKo6Qs1JSFpQnSAYVYX41YXwXTA1ocQtWxHoF47LHHWGfuv6reoXD22WdTVVWVr+v6zQcvfeh0D1Y/9etf/9pTUlJy8AM+geMHXIaSF2SNOZhz/NtYPOZpvjngZdJ3/xFtcT0nJk/hq9k3MLv6F8QzHfj0HGqr1+LZE0QkLdI7d7NsRwFP/LyO3T+cxbaX/0xDxxoArLTBr//i4dcrRnP5KzPI5BWyeEWCb56X4PYbsvf0B3/2DbS3baI6Zi/8ZFppMukouFzIkB8zy0ui0E2kXCfcX0cOP/gqsuszcdqsGBlpcEFgJ2M9h7+iZK0RQYsoxAsUVjbMZf3Tv4THVtH67PuEynbZhQrzmFf/QM8xG6LvUZFtJwquNhZz1zv/fdjn/yhnnHEGmzdv9k6dOvU/A4HAps97RuJjifyCj0kIIWYIIZYAK4CbgUnAZOwFjxYLIRYLIS7qTV3HVCQCgcBvqqqqxv7ud7/7TFMYexMe5kX6HvJxlhTI7i+BlpTdLiZ7QRtlz2QuaYdr6nFJtEySzAPDLXn/lR8BMNl1IVddddUBk/r1FiEEDzzwgF/X9VlCiKNuknm93h9UVVX1v/nmm4/oW9/W1sbKnU9RNOMKBgTbiXS74/7+5xitkRLGtI0iILKYZz3FeSXXAtDHM4DLB/43JRO/0lNP4YlnEFu0ntQme0yhODAcIVTOf+PrzL23jdtOC3JLdh2PjFzJhp+38df/K2LWD/LJyf4wH9YP73ycPL2UQld/BlGFougIv99ebEgIlLSBHjVR05KOkSYbTz74BM48xaLeUGizkuQovp48TIdDuRbECFq43ttCV7iGAlc/ahfMof7FGBu++QgA6yNvMb7y+n2O29a+iGFF0wAYP348pwy77bDb8FH69OnDCy+84Hv44YfLQ6HQW4FA4B4hxGfiJv5sEZiW0qvX5w0hxLPAVOBaKWWxlPIMKeVlUsrLpZRnSSlLsZdOnSiEeOlg9R2zHmqadkUgELhx7ty5vgMtV/lp8a8//pRNL+zgUCcONiazSIdduMJ2ZJNUwNQFpkdFTWTQO1N4W9NIFQyvnRjQ1Ql9ntnWU4c7c/T6XlVVxQ033OAOhUL3H7VKASHEJF3Xv/vEE0/4j1TMLiy7EZAEa00Wzh7LZWuuo+9No/ngkR2MjI9idv29/HHjXYwZeBmJbI1y/3H41GwWxJ9k5Ut2eonhfc6k6YPXyMsaRHLjJgBylUJUt5enhixgnOvDa5rJHPgzvdAfI3VCLnVDunhu7WwCajZrT2+l7X4Pm6/PQeoqWtwguCvN8cdt71X/itQAVS4vRerhi8MedpsRyl+RBDd1UKT0oy1tWw+ZXTVocfu5KrV7F8s2/o3i/DGEw2HAfmDIHnESAIqis2LXU5xS9Y0jbs8ehBBccsklbN261Ttt2rQbA4HAZiHEyUftBF8QZPdD4sFen0Oul1J+S0pZfaACUsrNUso7gIPOwTomd28hxGi/3//Qa6+95svLyzsWpzgkfnjx4yhC5+lNSWYO6/1DkSEVRFJFjdszgDMuBamBVDXcrYnuMEpJe6VCqsyewRsLKGgpkyFiNJvlKl43nzyqfZk1a5brySefPEcIcYaU8vUjrU8Ikef3+5+fPXu2t6ys7Ijbl5L2ggsb5t8P84Hf2tsDWaUsjbxAUb+XUXSdgJWFNDJ0JW1LYVTuWVR3LqA0ewzrG+2V/Iq1gbSwjmxRQFGiD/X+PuQN20Y6A0UFKuk++TSuaCTnwlPIu2I6I4sbuLf/s5SoH2YT3vmXKBPuLmD8aSeR1i1OrmhhwehlMBqq+l9B9mNeMn6FlmcGU5k9mA03HlX9/URK1CBnzlrIvNRkRm8sIp5ooza6hpbEDpLEmeQ6n82uDTRHt5AwuyguHsr27aspLCwk2WK7ufJOPZPsDXFWbJ1NTc036dev31FrX0FBAc8//7z32WefLb3hhhvmBYPBR6LR6Lek7P6Qv8RICab1uRSAg7JnlcLusOavYY9HKB8pc2f33/DB6jvqaTm61x3Y8PDDDxddeumlR7XuI6F08KlECxtpnGPgcvXuwz+9ega1K0sI7hS4IhJLBakIvO0mgc0dWAEPyUIPkRKN9nEZlJhKcLtC0XsRupYuZBkLaW5t4mgL5csvv8yll15aH41GBxzJGsdCCBEKhV645pprpt93331HzSV4fMlMVtQ/DYDi9eLJuMkbcDz6haegZnXfwC0I7IbO558lmeqivn1Nj6W392DsqMJzWNtirw89uc/X2HFNEUZnB75tL7P9zTq0/Hx844aSc95FhLYpmG6Ycfl7zCpcs0+bvrptOiE9ydhQTU8CvrCV4Nz1V7C7IYe/nvI3BuvhfQTm0yAhU4x47naG/i2G0hmDZIrqtjdIpLsY4TmZNyNzGFE4jR3hFSTTnZQFqsjvexwrt/wDgGDVWPJHnMyuF/5OoVLK7vD6Y9LOtrY2brzxxsS8efOao9HoRVLKlcfkRJ8T/IP7ymH3Xn/wgsCKc2Z9LtNyCCFeBVzA8o/u67YielfP0RQJIYQIBoOvXnnllVPuv//+Q1534FiyadMmqk6fitHSysB7b8HKLmTLlL9/4jED37gO7wYPwVqJK2zibUyghpMQT4BhkqosJtzPRTLXvqn1WZZEX7ODhq5q1huLGaqMYf0RDlgfiDPOOCP+zjvvzEokEncdbh2apl1ZXl7+5+rqar/Hc0QBTQCc6pnJDn8NuyPryb/9BlyDSxhZuBZPvo+HB73CedWXU1eXB4pEqJIBD8Obb93JoJyJVDct2G99EMuyEELw7rvvsm3bNq644gpcLlvLRuknE5VdNA2WBCZX4D3pFIJrdQpX2QE5iXwX7967f2r5LZkog/UjdxUdDZ6JBbl785l0LS+g/4sR1LpW0DUS0Ra2tL1Hm2zkzffmM3HiRIZ7J9JOE0NDJ7M1uZL68L7Zg7P7V/H2vx7fZ4XGo42UktmzZ3PzzTcnDMO4K5lM/u+xnrfzWeEb3FcOu+eGXpVdee5dn1eR6AD6HmmU2lEVCa/X++1Bgwb9z7Jly/wHWoL0s0RKScH405CZNHkTTic11s+OCw4c8ljx0tcJVetk7TRxt6Vx1bTaAqF0L3npdpEYlI/hU9ESFp76CG0bPmB15m1GiZNZZn38IjRHg23btlFVVRVPJBIDpZSNh3q8EKLI6/VueffddwNjx4494vZEIhGKskrIyxrEjCf7cl/VvmlGFiQFt6y4Eu8bQQr/P3vnHR5Hda//z5myfdV7sVzlXnAvFBtjG2x6MYQWEhJaICSQQnJzAwm5qZSQX8oN4VJCCBBKKAFsbGNjgw3uuMpdkiVbvay2zu7M+f0xK9ngJskythPe55lH2t3ZM2dmd+d7vu19l7egtLRhZqdRU/ERO5o+xEiEyNV7UxHaiq7rDHZNYLuxFl046ZsyloWb/05eXh6KomCaJoqiEA6H8Wdl8KtlE6jXc5lXOZis33lwVgcgGGbr94vZfUXXNEgORmWijamvf+e4xjgWlkQFt625Ht8CHzkvb4W4TVQoDYM6o5ItcjUFlLAlvI6LfTcBsDe9jm2NSzrG6OsYSW/nUBYFutdU11VUVFQwd+7cUFlZWVkgELji37EBzzOgQA54tHNGYsNFPztVjcQrwBtSyqOvho+BHktcCyEm67r+0zfffPOUNBBghzFKtKGEdpWx4/EHqf7+L9kZPnxIrs4MIjSJVO3qJTVm2trHpt2QBZCIBqGqHq2yAdf+IKKhhZ3mJwwSY0+ogQDo168fX//61zW/3/+L7rw/JSXlL3feeaezJwwEwLCSaaTkD6R8a/AQAwHwbP1kjAofvn0mwkhgpfmx3Bq5A6Zw1hn3MtV/NWGzlTxXL0amTmdbbBWTen+ZoennUh/ZQ1FhMR49hRxRiK45UBSF/JJhOIpySHh86MJkcFYdey7WbWpxVWHg00GG/uF2TFNiWV1fDE3/4C76vJ5g8r238khzn564TIdgqkuybvITcHEjIjsT4fOCQ0c4nWSrhUxgOq00UegpYYH5IgvMFylrWMzk4i8D4HKksSu2/nMzEAAlJSUsX77c+4Mf/GCUx+PZpGnaDf+O/E+nceK6HS8DTwkhGoQQuw/eujJIjySuhRCpXq/39eeee+4QfYhTDZmJTKykh2wFg9yycBrvXXyo8M9GIxXVafdIqFELtTVCS912qgIbUVUnHi2VraEP0aodSCzcih+fkooiFUxxdI7/nsL999/vePLJJ68WQvxCSnlkvpHPQFXVOfn5+ef+5Cc/6RHSwMnn/Bct+iaWPZcL2AuE10Jevr3ELpxQwirCEnirBcKUBAemE8pXaestSeTG0WrdFHwwirE78mmo2Uh523pyvP3x+vPxpRSQLUciIgZtdbtpNKoZ4prKrvgGzIwM9Esz2dyajkdPkO4I4SoKEu6bhndrArG9goLNYRw/22nP6Zl8Lpp5aKjpK5VnsXp/MUOya3mx76KO5y8b/AkLB04k770G5t12Dn+Zfj5bb+mZxHb/52/Dcltk9GrhmeFP09rmJivNQmZ4kap9ndRABG8oxtA6Bx+E/klvfSgDHWOYH/orH1Y+zb59P6empstOZI9AVVXuu+8+ddasWb4rrrjiTw0NDRcLIW74d2nAsxPXp155axfxW+Ae4GOg21IDPRJu8vv9T1x55ZXXPfXUU8cf2P4cMGzk9WzeYK+8fL0HUbs4jsv16S9EZaKNCx7/HhlbLby7A1SUzWdPeD29KcXEpJ79GERoDjcRDoc5J2c2tVRhWnHCBGkKNeDxeE74ufz0pz81H3744X+2trZ2qltRCOH0+Xx7Xnrppfzzzz+/28edqV9DTEaozYmws3k5va4dxZe/lc7OcC5LN5ciDAVn/YGehYRbkrrTpioRliScLwj1ieNMi2EEnDiqdXx7IbXcwFkVQASSjW1Ohx3eS5ggLcy8dKI5LlYtf4xog13h89sV44mnplEWymdVTTGte1PJWK+Svi2CXtHI/PJHKHEPp8m3nU3z8ikq+LRtfDKQS1PCx13pZTiTZLsfRi1uevkOit5L4K5oRXocGOku2op1sr9cwVul73T72rVj4NO3Y+TEmTFiC24lzod/Hkvu4hosrwvT77AV+DwaCY+CXtnIktW/ZKxzJqui84/72D2JcDjMl770pcjixYt3tLW1zZBS1p3sOR0v3P0LZJ+HbunUvlsv+8mpGm6qBIZLKbtHCZDEcZtKIcRkTdOufeSRR04LAwFgbT/QxxAsL+POH9Yf0kPRS/Pjr5R4K+YrDJUAACAASURBVEI0VW2gOrKVcUyjRAxkl9xMQDYRlRHcbjeZmZlsMj+mgN6YmHhFCmd4p/Dzn//8EA2Ansbdd9+tWpY1RwhR2pn9nU7nPRMnTkztroGY5b2RWd4bCcpWPjLfpTVcTa/rb0OOuoynVpzNBysHozdqOOtUnE3gbAItBFpEEM2AWBrE0gSmE4QqMeMq0hRYOoQKoX6EAxFP2OXFB2+KAFVFqgpxj0Kvqw/8gJf9bhMjXZXkOgKMytlH79IamqYYBItdWHlpjEiZTk1sF1raMIZPreSB3zQyf3GI7/6knl3lBtf5q/hS6voOAwGwJVaI5ZSgCtBVLKeG5VTw1JsEHyli8r23duv6HYxtN/2JkpJ6zkktw6vFaD4rSmhwFkrUQCqCeIpOLE0lkqHSOjYHhyOFcL/Pn0H5WPB4PPzzn/9033XXXYO9Xu9GIcSwkz2n44VEYFlKp7ZjQQjRVwixRAgREkJsEUJMTT7/vWQoqEEI8ZOD9s8QQryd3H/zcahTPgG8kuy+niCEGN++dWWQ4/IkhBAOv9+/7Yknnujdk7TSJxqRSITS7HFUhexyQdWh8H8PZXPDVZ8mUJvy7VtJ+6CSfTVr2Gftod48OgXDecpVrJFLiBFFQ6MNWyviRKv//fjHPzZ/+9vfPhcIBL58tP2SDK97161b5x04cGC3jzfaNZ1N8eUMGHQxXGyLJUmBzVml2iSIjlbQQ/Z5x9IFwRILR2EIlyOOqkha29yYYR3CKooJWLbCnHevIPuTGEo8GRLUVUyngtTsEIywIJSvEc4WtPzrX0SDjQRaK3njT25mTfNSYwZ5LTiQt2qHs7migLSVTvLfrWXPrgVsM9dSKPqRyPXT0LwdMxZGTfFz648yuWh0GwOKNVpaJbdvmUPj2z76bvejNQSxstKI9PLR0ldDC4N/bxxHi4ESiSN1lWiem0CJxovf+80hlVNBK8rFW+cyt2gNt6Ue+fvTaIX46q7L2bS+N2lbFTx1JlrEoqWfTlt/CzWkUP/4k6T3H82q5x/mZPGgHQt/+9vf5K233hqORqNzTdM8Or3xKQxX/0JZ8uvOLQS2X3H/UT0JIcRq4A3srqErgZ8DNwLPADOAMLAI+I6U8jUhxLOACXwLuAB4FOglpTxUf/koEELsOcJLUkrZt9PjHM8NzOPxPDB58uTvLliwwHM65q0ynUU0GdX4iktxhXax5J9FDC490C7w5YqzqfxpKbXz/kFANrLPOtI1P4CzxIWs4j0K6E05ZWRTQK2sOpGnQV1dHSUlJdFoNFpyNFff5/M9fOWVV97x9NNPd9vrO2vgHaze8SyDB11B4vyRdu+ImmTJVWxjoUbBU5/seTBtz6FljMFXx37Ij7LKiMgYf2gewsctfdjZlElrkxfRqqOGFTK2ShwBCwRYmuhQAgSQqv3Y0kAKgasiwOqlD5OVOxyprGHLu4WY3hgvtg1gfVsvylpz2NeYSs4rbnzLdrJgv82BdEbmHHa1fkwg0YBD95GS3Zdg2z5i4RZUlwdF01GEhjuqMy7zYkRmBqG+qQQLVBJOW3QqfbuBoymGEotDwkJEYmAYNrOsz4tRlE5rPxet/QWiNMh5fbYxxLOPO9KO/F0Yt+4qGveko8QUlAToAYESByPVlnWt//P/kurIY1vLUoakT2Nz04ktjuguVqxYwezZsyORSORH0Wj0kZM9n+7A1a9Q9vpV52jSdlz14yMaCSHEaOBVoI9M3myT3etfA3ZJKX+WfO5eYBx281sLMEBK+8YhhNgIfFdKOe/4zqp76Ha4SQiRD3zvySefPC0NBECpMgqA4N7t5LhnMf7yWiqrDiSdnylZSvVUjYgaJsWRfczxztEuoV7ZT67SC4/iJ4ciIoRP2PzbkZOTw9VXX43T6Tzit1oIkWma5u0PPvhgtw3EtJwvs2r3s+SOno6cOhK9zTYG3hqJd7/EXylJKbcft/NaRbIFoUK4bvTH/CjLFghyCydnerdxQdZGLi7ZxMCSGvT8MAhoOAOqZkDtOJWWfgr1owVNl4WpvyhGwiVwNZu20FNcksj1k993CoHAXmLaMMZfVUPENLnKv5378t7lW70XMji/lv1nAUX5TMu+Cb+SQWVwA2nZpQy+4vsIv4eW1j0MGHY5ViJOPNhKrKWBUOM+HFGFpdVPU1+5Bu/uVrSIxPRANAv2T3FQcaGfPVdksP1rmWy7q4Ad3+xD04z+tlzqR5vJeHY1ieparOUm7705hocWzeGhpsMry70Z9hBYn0XOSoXcVZLsdZLU3RYpFRaF89pQXvmAJqMafbgdydmTODFNcz2BSZMmsX79end+fv6DXq/3v0/2fLqLHqpuGgPsAJ5JhpVWAQYwAji4IXEz0B8oBYLtBuIzr3UKQoiXhBDTOrHfDCHEMSkhum0kfD7ff998881Kr169uvS+qdplFCsDWL9+/QkPwxwLKyL/YlLmFRS5B7Oh4g0cE6Zy7wOf1gqwNDCFiTgMp1E8Hmf9+vWsXLmS8vJylppvsM1aS6W1jc3WSmrZixMP9fX1J/xc7rrrLpemaXcJIdTDve5yub41d+5c0V3qDcMw2Nj6HlmFo8gadTYIEMnPTwpQTFDiEsW0n7O05KbCJRd8xIM5n64gazR9tJlu4lIlYSlk+MMUjammZHg1vUtriOcZGKmQ8FukeiM4nHGQHJAbVWwPxT1lPAYRPP48GlsV1q6Lk6l4SVVU4lIjamogoXGUH2dKFlPyr2Nc0dUMLJqFNyWH0hvvY9Cwq9m44nGmpV7XMT9FUaiRFQxRxrO25R3ayreQsagCGU8g2r+2wt7UqEAx7HCZlawXbE7UsCH+AeV/+BW7HvkJsep9uOoUPMrhG+RHOmoRpUFb0GrtZow1G9C37qNp+QLeX3o/O6oXMcp3Hhve/z25xeOItNVx5pyfd+uz/DyQLJP1pKWl3ed2u+862fPpDqTs3AZkCSFWH7QdnPHOAqYD84Fi4CngNSAFODih3JZ87rPPH/xaZ/FN4EtCiE1CiD8LIb4phLhBCHGjEOLbQoinhBA7gKuAY7JDdqsEVgiR73a7v/LDH/6wyw0RGjpuvIw+YzQuvJzpu4x32/7anWn0CJY3vNzx/3s/+zmjR49GSnmAGkKBbEcvdkc++dTzVVVV9CsegI6DEAGefPJJCuhDsRiA5YAmWcceYwMNVJOTk0OqyGT19o/o37/TC4IuYcyYMRQXFzvLysrOw/5CdkAI4Xa73d/64Q9/2G0vYtmyZbSZTfSdeCcJ3b4GwrQNBNDBhmtpYDrsUBFAJE/yYW0fHnM0k6u3oosE/2ocRWUwDUXIju0vQ55lqG5Xg32v9gwqajJJpJgoqQYWAmtjClIBw6eQcAmMFIjkguVKoX/Vdex4/ynS84by6msbmT3W/uXWJFKpCaTgaFbQohKjKB29KYyIJVBbw6SU68R9Gnv37cSnpOEQh16eLL2APuoZrAnOR4QUUv6vF0WX30w0E+I+QICz2aaSB5voMTCumFVv/pE0ssnNHA6j+rH/9b/T67rbeHj1DEomP88cz4FK0VuqJrNw9TBSt6pE1q9j565XkZZJ3Iri0zMZ7ZtFllbE/OYnANhf8THjPLPwvr+tux/n54L8/Hw++OADz7hx437lcDhaDMM4Ns3uKQIpQXa+BLbhGNVNG6WU7Y0sfxRCPIBtPA4mkvMAzdihps8SzLW/1ilIKfcDtyS1JC4CJgK52Pf7cmAxcJ+UsrYz43XLSPh8vv++6aabRH5+1+m3FyZs72ZK/1tYvusvbPadOl/0RMLW8tm2M86gAXZuYufV/4txmeTMiwLkXnIVdW+8jJSSWQOuxq9mMEJMZnHiZS655BK+Ir/yqfEaGxs7EoytspGxQ8+i1ahBV92kiUxKHENZFeq5MONtt93mu//++7/OoUZi7oQJEzieZPUDsx7FkibeZogKy75ZJ5lv28tapQJCQsJjG4iWMQYOn8H+mnQe2zUT6bRwpUXxugw0xaKhyYfY58JySlYV9GaoXsdGI8InzQVoDhMzVaI5TOIJlXiaRaJFwRGUqHFQTIFUJZZTEh+UifVulIFpZ/LByvXce38Djz6YTUPcj5FQsXSIewVGmg7CixqJo4QN9NogamWE8r1LGOuayfyWQ7vv26VB16xZw+2XPMTquldxlUbQhAtXvcDZYntQTcPA2SzI+ThK2ZI/41czqYtUo+s6Ukr6p45n529/wshHr6I+kcKvmoqoM1IY7qnijpz3KD27lj/Fz6P1yaUMKZpDW/1udoVWY1kJ1rR9+jsihGB15Li5HT8X9OnTh6VLl7onTZr0Z1VVW03TfONkz6mz6KFARznQUTaXbDpUgHnAMGBB8qUhwCfJ/dOFEBlSyqaDXvtDVw+cZGL4S3LrNrocbhJC5Jmm2S0v4mA4hYvM1P4UZo06nmF6FOPGjSPrsisYd/E+7vtZAzv32MUEDoegbvIdNC1+F7fmx6V52RPbSN+08ezR7B62a3LvOGS8ePxAfmOYyzYQAHEzQn2iitXh+ShCRQhBQ0PXJDEPh6uvvlpEo9HZn+X/T01N/e63v/3t4yIsCssgGVo+jsYIWsRCSGmHXZKbVMHSBZYqUAy7wgkpsCwBYRW9RUUNqkgpUIWFqlhQ60KLCJwNCr/eNJNLdszi+vVfZceefMy4QlpaGI/L/gws9SCv5WBIsPJ8eDKL2Na2nF7a3fztlQAbtsTwqDHczjgJn0U0w66KChY7CRV7iRamEPYkWF3xPF41jcX1rxz1/MeMGUOmuxhP7/4EN67BdNnd+EpcokUl3mqBkSbZFv6QhGIxqeTGDi4qIQS7AqsY6pnClu++xYOLJ1JnpLChuYBfbpjFqkgftobyUCMKctwAdtV/gEhWdznFkXttRvW6HCEEBRkjmHXG/d34VD8fDBkyhEWLFrk9Hs/zmqadc7Ln0zkIpNW57RiYBxQIIb6W/F3eCVQAfwXuEEIUCiEGYlcy/V1KGcKuhHpACOEWQtwM+LEb4k4KuuxJ6Lr+lblz59IdL+JgvLfjd8f1/hOF+ldf5swBtxA2nmfynL3MvcTPVRf5OPvLrdQsv4vGqrWk6Xk4XWkIXac2spMsUXDYsTIzM+ntHkGLUUOKlsWQ1KlE/YLG5h301YaiR6DZrMUkQWpqKgAzFLsnboH1UpfnnpeXx/Dhw+OrV68+F3gLQAhRmpqa2nf27NndvCI29lsV+Cw/SthAMb2oMVu6tf3GnXALtKh9w1STtlGv1bF0DUfUbqKzEnbcXlUkjW1eUCXCEmhhUJb5qZR+FCBFQOswKO7VQjihUxNIsV0UCXGPTddu6qCF7UWZVCW5X72Z/Y89SmtRX9wTr2bOdf9gyzKdgYP28+3aL2GkKsT9YHokRqiV8HsrCWxYRoqewYT8G/D5jm1D39nxa8YXVrDhrffxzxhDWHHgaFVxBCV6G0TfXUnTx4sZM/5O5n/wq0PevzH4Pn3SxxN6fC0vbCglXltO6uQiHtpxKVoEHBYUjLmAyI4E+6rXcob3PDL0w3+3AHDZ67T9zZvISz+1WxPGjh3Lyy+/7Ln88stfEUL0b6ezPqXRA56ElLJZCDET2xN4BFgFXCml3COE+CuwEUgAv5RSLkm+7W7gWaAJKEvuf9KIFLtkJJLU0rfefPPNp03jXHfwwY7HgcfZ/OZXeb6hhn/cu5TW0D8hlMAyo9w018GY74/mkbcvZe99ZUiZYKlrIU7FQ46zN5tqVpCamoqu6+wJf/K5zn3u3Ln+bdu2XUnSSDgcjuuuvfZa9XiEn3bt2kU91ZzpvByaW/FsMxH9MjGdAksTxL0Kakx2JJaVpJHwV0DCJWxDokA8FRJVXuoTXlRD4IiB3gaOoK3spxgSqUE0TcGZFmNYyj7ClgNFSPYLSUCkoLeoiOTPRVigBwXRXnHyRrbSsmsamz9eRkm/mylfkcF7H4S59HyF0TMfpSLhpyyWz/+8M4rGh1/Cb/gYkT+HFduepStcYx9XvYA3o5DQB+vwjhlPNBvyljazv+w19se3MJyJrDiMgWjHH557gAvnXIhY/wGWFSc7XEhKVh/UqEQ1LIQF0XMvIl6dy4blb9GvYMYRx9LT7Iq7VG8hYbPTIeuThlmzZnHttdf6/vGPf/wZOHV0BA4HSWe8hM4NJeVK7PLWzz7/IPDgYZ6vBWb2yMF7AF0NN410Op3ZU6b8Z4hULd7/JM1vvk397jYGTPkKAy+4nSHPfosdexP8+RsbibWuJv/eu+h9zZ30P/tGRk26g0ajikm9L+n+QYVib93EnDlzhJTywvbHbrf7hmuvvbbbWhFSSvr370++0geXOw2cDqxUj33jT3ZDK6Zd3SSS1T3tvQ1aWOJsleghsHS77l+NCoQpUKPJhG9SvubgBDjJ/0vdNUxNKWNkWjW6ZoLXxHRLSOY+hAVYkJPfwldKljPpziz8RaXsfuohZCjMy0vsIpGoBcuWJXjo5q3su/9pcpUSRpRcztryf3TJQIAdOhpWOpem594hUdWEVKBlRAYRh8Hg7Ol8Ipcf9f2zZ89mIjOZYs1kcOEF1K2cj7PVRItaOAIJ9IBtYf0TJjB2zO3s3jGfERffd9ixVn78GOlpfWkNVbGtYh79U8YzzX9MobGTikcffdTp9XovVFX14pM9l2NDdHI7dSGE6CWEmCyEOPvgrStjdGl56fV6v3rzzTc7jlfi8nSDEIIt/3y447Fxyc/oO+ESAv98n1hFPUYoTu7dc3GGJuJZk4brGNKWDQ0NeL1e3O5DVfIWmC8e11wHDx6MEMInhCgBTK/XWzBp0qRujyeEIE8pwetIR0oLYVokfA4i2RoJt7BLQGMSJWEbBkulo0TU1WxhqWD4FZSYQDhASRoBLQhaxE54C2kbEdMhsByCaCZk+MIU641MdUnqEzXMNwehaCamX6BGdPQwYIGRBi8Me4remp+vptTCq5B//5XUPf4Uf38GnEYtf33NRHEa/Pc93+IHS36ApmnMcl3HLNd1HYnprmDlx78le+wG2lZ+iP+W6bRYKeS5+rGv7dhFGDOUq/AKPwuslzAMg0x/IeUfvsjexjUU50ygNOccMupDqEYGLdPyyYlNo3rrwiN+NrV1ZR0aG7vaVrGLVUz0tPFR+F9dPq/PAz6fjxdffNFz/vnnPyOEGCClPP5k3IlCtynxTg0kq6h+BOwFDiZelNjJ8E6h03f7ZFb++htuuOHkClafAnA4HFSte4fA5mp2b9tDhq83db97GW3rPgwriqIefuH+ySefMFSfSHZ2Nh6PB4/iZ4r30h6dmxCCs846KwGcBcycPn16QlUP2zrRaShSoSVei8xIIzyikOaBLqKZgoS7veRVYOrJfonEgQ0pUUxQDYnpBjNpE53NoBq2URGWrR8uLDBd9phShdawi3mtI3gykMvvd0ylpc6PtAS638DIiWM6wXLa+/bWPq0mN3BuJnmFdkXiwleLmKRfwMaPlvOPh5dQ4O1Poav7VV7tKOw1meCHa3DX7sJ02B6X0kUP0OFwMMA/geqm9QCEwnUs3/Zn4sEWVEMiTEgpHkyw5sjMzpqmMdBjU6O4FR8ChY8jb/HKK0dPxJ9MnHXWWdx8882elJSUUzMxCcmCDNG57dTFHcA4KWUfKeXgg7ZOGwjoWript67rrsGDB3dtmv/mKCwspLFtDxneElZ++BCWsAjJANNmfTouPXzwlxg9eiz7zAM/eF04WR5+ndT03uQXjSPVmYsQAiEERWr3+ynOPvtsn8fjmZiamjpj5syZ3m4PlERfhhKVITa3Lqa5VCeSDYYfTFe7BwCm0/YqlIREmBItIjsa35S4zesUTzNJ+KT9+1Ow9cLbKTeE7YW0h6siLW4WVg/kb3sn0FzjR2vWkBHtwM7JMRLeQ5d75+ZuJ33SdASCkBJkhfouE84aToOxFwEEEvXMjz7XLS+iHetf/Rnpl1/E9offRRiSSLyVcLzrZJsra17DkiZpjnzGZ19OrrMvH1U/R+3mpVhV9ZQvfIaMoiOrzY3TzmVb+CNGO6cTsYLI5PL32qtu6Pa5fR64//77HYZhXC6E6Flt3x6EtDq3ncKoByqPd5CueAUTJ06cmDhdKThONJavmcfAgQMJGY1UhD6hYX0tPv1XhBLN9HIPo9bcS85ZF+K86kxCP/sN8Zpair77X7ClCkd1gLa9Zbh9fclhADubPqRJ1hEMBjtVdfNZnHHGGbjd7smJRCL7eEJN7VhmvcnevXsZMGAEVv1G3IXDQIAZT+YWmkCLShxtEj1oZ5WNFJVomooWsw0GgJYRxUpRaPPrKGEVNSxQY8KulDKSXdsJmzXWqtVpSqTSqKSgBjW0sEAPalCt4YzZvRltg+Lsmf3EIfP9cdZWvvHYai694qvsWRNi2nidGUNq2BnJ56VfNZC+tGciHHVP/p1UTx7q66spa/sIgEKlL4MZy0Lr8GwHn61aay8oaDH209Zcwa7W1SxdupRp06Yhtv2LAcootm19/7BjnadfwxprCQArQ/Ppmz6Wyrb1pOg5BOJ1jBz0JT4pe75HzrWnkZmZySWXXGK9+uqrNwO/PtnzOSxObS+hM3gC+KcQ4hdA48EvJJPpnUKnjYTX6z172rRpn69K/GmE0tJSTNOkZMC5VO1+n1i0Fcuyk5CBRD1F7oHoEyZjZEXJ/f6NmLvDZK83cG8XoGeSU3iu3XtgJOirDmFVy5tk+rMZpkxkjbm4S3MZMmQIbW1tgyzLcvSU5nFxcTF9zQE0vrkcT9YwAsNMtFYVR4vAEbQNgTAP8BQoiQMUHaYDPPshHvCiGqDGkpThGbaH0ZH7a+e4lBDPTHDOyDKcSoKllf2wtviTZbc2gaBigu47MilmpuJl2dSl7DozyPJIbz5sHcD8TYOJvf8H0ide0CPXRFEUBrknsHrd86Q7C2mOVdMiG2gQ+7o13qbgUoQQTJ06lf4MR0Gh2DoyWWcwyTJcXV2NqqoUKf2oZD2BeB1ORyo7yud/mj3gFMPdd9/tfvvtt78lhHhIylNvTS56ppnuZOKbyb9//MzzEug0C2ynjYTT6Txz3LhDqri+wEFQFIW9u5Yw6uoHqFz4d4ItexlWfAl7WlaSN3QajtUml39lER+W9GdNeDDaJxFbJ0ERSF3F0hTwOlBFNuMTF1LbWsZaawmjlDPxSC8qGsvkW8ecR0FBAYZhuLOysiK6rh+aHe8mcihmb/A9dr73F7J7XwfCgx4CR8Cyq5ssm8obgJYQwbpKYkYAzeklK3sovn12/iKSrWK6wPRYmD4ToUqUZh1Hs+j4YQ4srcaSAguBrpmEXRLVEJDMXwgLFOXYv2IVydpgCe/tHoA6rwraQvRt7B5/1eGwqvlNzvZdgUO4WR5/A124aFW7FnaakHIxW8MraE3UkekoYGjGdHbIDcd8Xzhbw1ObwtzBd/NB60u0GQc4wmKGPYfW1lbS0k49DQqAiRMnkpub629ra5vOgc7jUwNS2PT1pzGklD2iudtpIyGldKekdIVj6j8X6198AHig47E/qzeTb3iJX15qJ5DvSKtizl98JPIz2HNdARdfvpzr0j9is1HA/9s9jZpt2aRvySLn/WzO2KGxLbEGgygCBZ+SSql6BmvjS454/PbqM4/Hc3wZ689gSfwVDMNgQM4k6n7wKEPH3Igv7qG+ej3hRAuaNxWPO5O6+k001G8hRWTgVv3U04iWVkVR0WT2Domjz9b59dDXOviLAlaEu6tm8v7awSiG3VexsyabCj0DRbFImCpWfoyIV0drU1FjIBJgNLn4WcOgDnbZg9Hv5VsRcZt4z1cFhdsifLLkZfr7xrDww54lJl0atJPEo0quoKphLfnZY475ngv63MMnjrU0N2wjpc8gRtdeyJKap8h0l7Cy4VW2bNnCkCFHzi+OHHo92+oWk5XSlw9bXmZQ7zkURbI5l8tozDP5pOYNdM3T0aR5KkIIwe233+574IEHruVUMxLQI810JxvJju0rgBxsyo9npJRvdmWM//hKpc8DKioZVa1ARsdz++cUk7+glvQpQX6Z+wngZrijmcLSV1mYP5QFpYMItGSR2zaC3PhgMC2saJTGWCUb4h8yVJ/E5viKox7X7Xb3qJEAuyKnomUNI7IvYMNHj9sNYVoxfjWDaEsFjYl1ZGkFDFIvZHHcvnlO8V7CyoZ5bGtYgrXOJNs1m1+6LuC3WpwMZwSXGmdbcw44LWRcRaoSM6wjXQLdmUBVLFSPgXTHIRccegKXniAF+FfVMAa69nOV78Dq/dv7x+CsV1DidtLcU2exd8PbqJZCfqKopy9JB9ZXdL6i6J09j1A8bBbRphoQgo2h3WSlDSRRmEVu4kwuOPsmKhoOHzYeP+AmyipfZ8B5XwO/h30vbyJmBFh4kJcZjUZRVfWUDTW1Y/DgwTgcjqEnex6HxSkXAOsahBD/jW0gfo2dxB4A/EYIMSrZyNcpfGEkTjAGXfotWht3M2rYAXqFoSuuI3dXHCyL+D/ybGb5JEwEEcuBYaqoboFZmAmWTcstwgbZgVRG1elsMD7ANE2OVt7qcDh63Ei0Y0P9O8zK+joSi3cbDiXGOxgfhl5nmv8aZEkhDSWSLc/8P7xnjyclI0FNIIV4XMVMqKBaIFTUqIJlCUzT5sZxuOOkuKMUpbTSz9fAAFcNfjXK/KZhbG3K5e2mEQxy2IR3jZaHt3YMxddk5z6UmEXDmsXUNGxkYs5c5u87Lq6zHsXeTfPpPe5yqjYvQGT0pa2xgqayPRSljaQlXIVlWR1eoWmanOeayyb5MS2ygfyrbkSW9KZl6WIyPSUM8n+6wdXlskkRpJTMctgNdu/GX/h8T7AT6N+/P4Zh9D7Z8zgE7SWwpzduAaZIKdsrnBYIId4BVnCYTu8j4QsjcQLR0NDAttcf44ar/MycaleiTt9yEamv+FEMg0RuKpnrA8yedTWVF2WghSCl0sTZFCfTMIn747T18XYotDmCFu5aum0plwAAIABJREFUD5mJBHrDagboI9htHVl85kQ3Pc5v6PwNd3GbfYPaunUrI0c+jrLPT0CJIU0FpVXD0ajgiiUb8pw2vYelKVhOlVi6iuYL88PitxjjONCDco1vGfSCzfEwl3xwB9S4cDYL/A3gbrBQ9jezY+MrhIO1jPVfwHunkIFoR3/PWOLjJHWrFlGYP4Z95SvY27gaieTdd9/l/PPPZ5b7Bjaqq6lN7CDVlU+ve/4Lz4QEka0wpK4vC8NvUrNvHSMKL0Kg8Lu/38P1s+8gRc+hzahjb2ILU9Q5J/tUD4uSkhLC4XCGEEKXUsaP/Y7PD+I09yQAFQ5RPWvlIFbazuA/q3W6i4jFYixYcPhQ6Sz3DR3bkVDafwIFo7L4/S9yABj0f7fT9FoRCSeYLgUsCaYEy8JfIXE3SNy1MYQlSXh1ex+SFBQdjKt2BZGWUNgn9zBBnMd54srDHr+g4CjkcEeBZVm888473XrvsXDNqFtxp+WhRwTqfif6fgfOBgUtTEflk2LYOQclbgv6EFEIxRy4ROKwYw7VPTw24QWUuKDw/Qi57zegryhj7fLHcAck45nO0uYTv4qurKxkw4ZjJ5wPxsL3f8jw9elkefsiVYVpg+8hkzxcePnZBQd6zeoje5gw6GsMmX4HVp6HWFxDqpKg0+Y12R1Zy8Z9/2LDvjeYOnUqVeEtaIoTM8kLF9RDzDjzfxh67X8x/uKfMuWqhw87n88bDoeDjIyMKFBysufyb4jngJeFEOcIIYqEEBOBv2GLHnUaX3gSR8HLL7/M9ddf3y0FvdGT76I1VE75y33weRXurRlNydshlHAcYZpgyg5lN4CMFfuRLa0IoYDXjZbqw+HQsHSVWJYT06mgxiVqyEBGohTTn/1UsJJFOHBSLPpRzACWJ2Vwy8rKyM4+tuTq4bBr1y5mz559QpQD681qctUSPLXQ5ha2UJEOWtg2DCQV7VAAYXsWamaM/xn6Woco0eEwxxPlR0Oa0J4Dc+9e1rS9QS+llDJrTY+fw5Fw5ZVXsmbNGkyza4Sd81qf5Jz8r/Bx9euklRYzaOBlfLDtj0gsZihXoTgc+LQMms0aMlz9KVwsUaNOPGX72Fz1PvlaX/YnPq2/Pko9h+xgBkKNsY9teONeFn74I/gQFEWjZMSFXJC/m7b6ciSSDxNv9+Sl6BK8Xq9ZX19/5A/3JEGc5tVNwH3A94D/xTbC9cBLwI+7MsgXnsRRcLAexGcxP/Jsx3Y4RCJNWAmL5avsld5rm0ciTAuRSCDiJsKIQzxxYEvYf6VhQCiCaG5DqW9Bq2vF2RjD0WqTv4lwDGma5IoiRqiTGaOeyzj1PBRUVjCfQqUvw7SJ7Nix46jzP1lII4u65q2IcBwpwHRJEl7ZIfsJ7doU7Z3ckszU0KeU3I6EhKkSi7axIvgGKUoGZebnZyAA6urqsKzuxSg8Wgr9h1/Kjl1vYfUtoK8Yymrep0Hux4onGJxyFtt3voWxrxqtPoirvJl4SwPV8Z2kXXolQtdx59ilvb2dw8kS+VjSJEPNY6TrHKIpUJBrV11ZVoKqbe+xuXUJq8xFrDGXkO4pYqB/EudkX3/Y+a1du5a77rqLWOzw8qvHg2g0qgCRHh/4eCC7sJ2ikFKaUspfJKk4PFLKEinld6SUnw1BHRVfeBJHQVdXhAfDGFUA62F/cwzwIuqcYMXtigkr+c0yLbBMSJi2kQCQEmmaiMiBm6IWDKHpuh1qMk2EqqI4XahuF9meAkgkKA2lo0dcaNJBg7WPm+beSSBawwDPOIoSvbpEQdHuQZyIRqxNxgoK/YPZ9d7TpI+4CSsNhCox2xzooWQ0TSVpOCR4TAZndEplkVCtl/K6t/HgZaj4/Ht6jsfzemfvYwDkF49ny7pnGTviShwb5rFTbiKLQvxhJzmO3qz/6I8kpIFT9SKkwMK0vzNxg0jdXgAsXUF1e9kYep99oZ32AT5jY+ORALVFLZQ+ejfRrdn4/7KShoYtrGh8hTR9AUWugRQVTmZe2S8B+PrEe1kbX8Lvf/97AoEAfn/P9dWekkYCTmkDcDQIITZIKUcIIbZyhLPoCn/TF0biKIhGj716PRKa1n7A7bf4KLkgk6mbLyZjMyhG4lMhpg4oCui6bSjM5EpUVWwqblUFvxfpaOctkmCmoUiJ5dSxnCpKJI7WpDMgeyZWupecQh8Jt4Ioq2D9xqdpEBUMVcdTqPTtVIVLJBLp+Ovx9GwUQFEUKls2UejtT+IP/8J3/WXEMiRxr8TSbHEiqWAbCIeFcJg0RL28EvJzhbft6GOva6SqdQOTs+ayoO7z1023LMvEThZ2G3v3LCe/YBQrdv4fhX3H4qysQUvP4J3aPwG2xG44HObc1IvZRzl//OezXHrppaT7XqAlZBuJyuAnrG1YRCKRoLy8nKKiIuLxOCtWrGD06NGcM2IOIS1EcH8taX97gke+q3PG1300mGFeaJzAbx4bxN7nXqM1ZDLdfx0tWgtVzmpIOqZPP/00hYWFXH755cd1vdoRi8UOl2A96TiNE9d3Jv/e1hODfWEkjoJ2I3FwKWJnoXn9vPRKmIvvOcY3TQg76GeB0LRkK3HSOKiqrd/gcmB5HViO5ByS9NpSEbbIj1ND1VUQgoTfQaBEw0gFj683kxqvY3/9erYZq8kSnVMTDAQCALS0tPS4kQDQdZ0NlR+Tn5/PyKrZxLJ1zKw4UrUwwzpKxBaMkKpEd5g0RT0sahnCZd4VKEeIkG6Oh4msXo+v31CW7Pj8DQSAaZoWx2kkNE2jrnYjQ/tcQtnut5DSYmnTC/Qf3YCqO7nrhomcd955rO4QMbORlcjCUsIUuAZSH6/A6/XicrnIzc3t2Kd3794A5BjZbDR2cSYXklewklvvaGb1/BSaLEFASWHYjS6CW7/MqtV/oCr+aX2MUb3n8uvv/pGqWBm/+93v+MY3vnFcVXRSSgzD0DgFjcTp6klIKZcm//2OlPKig19Lsnm/ChyeEOww+MJIHAXl5eUG4GhubiYzs2tklaWuiTSM2swT36lhyV9e54IbZpPYno0wHSCTXoWRQETjYCQ5iBwOsKykB6GAw4F06UiniqUrxP0aCVc7bSodSmaWpiFznAjT5ksydYjkWiTcCuq5A8ir6sX+j6oJZXZOULCurg6A+vr6bldIHQt5eXnkekrZt3c5M27Lxa9FsaRCRSidmjY/QoBbj5PlDqEpFqGEk6VRlamuw/9y/1A3jUyhU1a+5ITMtzOIx+MJQD/eMJ0Qgi3lbzDSNZUNsfeJyjC71r0MwHdXvUZMRihQ+pCTNZSclIFE4s30zp1MiZyIGjPJ9gzj4rN/jRqMYlSUo6LxbuivHdK4PlIppj9O4abyT8NZxyKmDBiMftZkzG81cPvOZ1l5Roit1miaP17GmJTZGKEWskQB7+15kekZN9GaqOeb3/wmP7r7JygojNbPZVGs6xVkzc3NaJpmJBKJ7rvtJwC2qNXpmbhO9kJIYKYQ4rMVCel0sZLsCyNxFGzZsiUKOGpqarpsJD5876eEw/cxekQar/yrjXcufJtJJbfhakygxiwsp4qwHKghA6VNgGnauQpF2OEnTcVy6iRSnbT2d2H47UogNWaL/KiGBKEgLIhkKSTcNjOqsAAF1IhCPNWidpKkbZtCcGkDPn/nPImampqOvyNHjuziVes8fvrovXz3Z4+ikEO2I0iqFubSzDXkqQGiUqPR9BG2nCjCop9ezyjH4Y3ceiPKsn+Mxl+zBrfi4/yUrzAv8NQJm/fhIKUkEAhoQgjZ0NAgultZdjA+iS6hsbGRhQsX8uOvPkKINpoSNUgjRLW1i+q6XRREhrKv7dBemQGJGeyossu3x7jO+9Rr7RVwAMXCpqRfFXyHnHc3oix2cFOsifTx59CyYRnO0t6UtWxmR9mKDl37RU1PA3Cu8yrqrGo2J1bwnvEiI137+STa6QUqAFVVVbjd7lNTeOg09SSAF7BpM2cCn1UxSwAfdWWwL4zEUbBp0ybF6XTWVlVV5Q4d2nXmAI/Hw6MPZnPPj+u55HwfjcMEWRtUnC0gTDtkJBIaIuGAeDJJrtm5CKkKLJeO6dawVPEptcR2EjxLt8V+DD+2kUhWW0j1AAmeFTOofPOvZKcMwOXoHPdWZWWlCahVVVVdPueuID09HSsSwaUY5DtayNNamOmOomAbg4hsJS4tUhQ3cGQvyCsSCAv8WX2IV4VpUmtO6LwPh4qKCnRdD/l8vupNmzYNnTZtWo+Mm5mZydVXX83VV39aEvrckjtIyBgxGcHnyGR7ox1hKHEPx+XLZlvVAgSCUcVXsqrCvk98lqYcYK+0E9uBQIBRaZMIRlsZpk7EMegCzAFuWl9cQCwepaCggDP9V7IscGCM92L2/2lKNq2ygT2xTV0OzVZVVaGqanXXrsrng9M1JyGlfAZACLHlcJTgQog5wK7OjveFkTgCWlpaaGlp0V0u13t79uzptnDw+ddU8dAfvTz+bCvv3PAbLuC7ZK9vl/yUiIRmh5ewE7ZGmgM1ZqEYFlITmC4FLSrtfZK6zu2eRNwrCOcJolkSyyERprAFfjRAlagBQfOf/05qQKeicU2HdsGxUFZWFgb27969uz8nsEz60ksv5fovf52sfWXcVtySfPbA4dzCibsTHv/bwWGER0cI1KZTtHM4tdbhqbobGxvJyMg4IXxG69atw+VybYzFYtvWrVvXY0biSHiv4tPszzML76AhWsmbG/7Ml0Z+DzXjXAq9g3m38veALZuKy8nCyHP41AyG+KZghSN4lBTej75CSkoKr659jjPOOINisx8rn76H6VOjBAbl0Vy/g5q6dRxpaT0+5UKqI9vZYixnmuMy3k+83unzqKqqwjTNPcfe83OG5N+BKrxKCPEb4OAwiA5cDHSa+fELI3EErF69Gp/Pt72lpWXjtm3brqKb10oIwaB7xvPTr3/AxbOK2f7lP/HtmWOY/8Z4fHsl3v12U127FoNiWLT2dpDw2s1l6kGSCcICLSZtwR+HIO4RGClgZhvk5ATI9bbhUhNsrMmHDX4Sv/obifh+9oT3d9pAAGzfvt0CFm7evLkA6LrqUSexY8cOEhh8s28D3bm8uxJBXg6M4o2qEVhNTgyfQGSmQzx0yL7TUq9lSeB5Rvqms77t8JrRx4OPP/440dbWttQwjJ1Lly695p577jlh1+1weLf6gNFY2nBouXNCxlkVfTf5v8Hm4DJCZgvpIqdjn0vH2muh/YpN9bNoyQ87d+yW7of2du7caba1tW3t9gAnEqepJ3EQngYasJVaioGVwHXAtV0ZpEurxM/Wgc90XMtMR5eOd9pg8eLFZjgcfseyrC3r1q07rsqLP1y2hMvn+Pjl/2sG4NH8NWy59U+ECgSmU0GqB1a2WsQOO5kOO4Rk+CHusR8LKUGCpQniXkE0A+KpJqrTbNf6QRESSwoy/r6FyvhWtuxZj8NxeM3tw8GyLHbv3u0BXt20adMJ/Zmced6VFN10JrnZXTcQMRmn3nShJle3wkr2V6gWOD5NTTNz7P0sCTyPQKHOKO+JqR+CefPmhQzDWAwsW7p0qXIiutW7gvNTvsLIzAtIV3Lpp41gu9iI7vAyc9gPmVp6J1OyrgEgVz2Qw4zIMH2dI9lvlTPOM+u4jt/c3NypvpGVK1cGTdP85LgOdoLQTodzrO0UxkTgq8BPgbiU8gfYBuKOrgzS6V+noijB1tZPi6m8a/y9K8c6rfD222+HotHoImDP5s2bj5tN9a3824g98RB9S3S++bU0NE2w+Q679r106Y3kveDCXRvFctjJaAQkPPbfdjLKCLYojxRgOSWeQc1Myq6hKeahPuRjbyCN1mYP3g0uosFG0lwFFBd3TWCnsrISXddDhmF8VFlZ6UkkEl3yQjqLeDxOa+Nuyr4Ro7NVozEZZ2HEj0vEyVEjgE6W1sbQjBqaCz3E6vzEYgEcjgOL+DP7fp2NoSV48nqjZ2TSuK+ix88lFAqxdetWD3ZCMGwYRnTHjh2e0tLSHj9WZ9Fi1rGhbR4FKcNoibfSFKlkVJ/rifZOQwsmiDSVA5DiOuBJCEXgcaaTY5awOvIu9fX13aZ2ycjIoI82jN3xjUfdb8OGDTrQNcKrL9BZhIBsoAIYmHxuNXBOVwbpiujQvhtn3DKy2up0vuO0RVNTE1u2bHECy4BYIBDQmpqayMjIONZbj4i9v/wlvYTC/MWP8fQLAX7yvUwuvcCLEILtZ/+Vvk23ULjIjRSgGhJPja0brYctQrkabb0AAZYK8QyTzF7NnF+4lV7ORpa2lLI/kMLAzHq2JHLRwi5C0XrcSte7Yttj68FgMJSamlq/devW/J6SQD0YmzZtQk1LI5waBjo3z+3xBMvaBvJW+VDCQSeKZuFyxZESwg0S75/epLFlI+V7dyKlJNtZTMBqImvEmWRNmcXG338HX+9BPX4uCxYswOfzrW9sbAwBpKamvvP2229fd7KMRKkyih3yE4rGXkj22HNJ3RFFrW9D+L0kDAukJCW1F8OCZ7MhtIRCpS/9leG0mHUMyJxBYa/JrNj5JGvXrmXWrO55FJlKPjVm+RFfn6ZdyRLzVQR4sG9ipxbk6Zu4Pgi/x164nAVsEkI8h52T6JJR7nS4yTCMvV7xnyFxPW/ePHw+33IpZURKafl8vm1r16497nErf/Fzyu/6Pj//r0y+/2ADt3+vjkTC9ld3X/o4+6cIQnkKMrmwdrSaOJoNPPUmWhQshySebqL4DyQq1OQ3OcMTRlNM4nEVV4NJbXA7WUpel+e4evVqKxAIvA+gadrqNWtODP+R3+/HisfIFJ1jLa5MtLErnmW/1xXDiqmIcg9yZSrBv1VTc+evaWrdxTjnDPLz85mUeTkRq40zrngAzzUXEIhVo3tSGXjmTT1+Lq+++mq0paXl+fbHgUDgpRdeeCHQ4wfqBKSU7JB29CZ15ATiXohmO7CyUjCTGlRSVbDSvBQVTGBSymUALDP/hQsPWv/+BAZnkDZgNDfe3LmcxOEwwn0Oo9yHT96f6bucJeYr6Oh4SEGe7NjckdDD3E1CiKFCiJgQIi/5+HtCiIbk9pOD9ssQQrwthAgJITYLIc7s1vSl/B9gBjax303AHmA3thBRp9FpTyIUCu2ac/e0RFfec7rimWeeCTY3N3cw90UikcXLly8fdt555x13pc+OK38M/JjxM2qYeW4J8xaHuHCGHR7Zec3/AnDGz2/vSFirIQN33CLN4WHf7ARFhY20ht20BDws0QYQznagCYt8b4AWw41Z6UVds5UYUVbUdb7KpB2LFi0KxuPxjwCam5sXLV26dMZNN93UuS68LqBPnz648rz871/C3HvbocNHZAxTSuJY7Izr/7+9Mw+Pqjob+O/MnsmeQEASQBaxiKIgbli3qlhrrbbW7XOra611w7YuWKxLa1u1rqCIWMQFUJRFUKRsArLvshMIAbIvJLNvd+77/TGJRiCQSSYk4P09zzww9557znsnM/c957wbtXomlztruTp5PXRaD6dCj8/vwjR8IuWRLSxYMo9zzjnnu+t1dFRWJlcM/4a/dthKxg3JpP5yIKs+eCyh9xEOh5kyZQq6rk9pcHj2unXrbBUVFeTk5DR6baIJhUKc2vEi0mw5nH3iXUS3K0oHgyfPhD/Hjs0tWIJ1dcg7WFHdkzFpOZxc1JsTtm7GlpbNnsE2gh11kqu6UrZzCWd1vIbllU2vuFfPPO+ERs9ZzQ66mHuiUNTYS0e24JZbDUViVxJKKTPwDmCre38x8CCxWb4fmKuUWisiU4HXgAogF7icWLrvbiISPmjnjY/5OjBRRDbXHfprc2Rv8kNPRAq3bdvW/kLnE0xNTQ0LFiywisjk+mOBQGD+7NmzvYkcp3Pnzgy50MnGLQf+3YMdIblMw14VREWiaE4roTQTlnIbRdtz8O5OQ0qSKNuXRq69hj7J5fR0VmEzRTF5dLaWz6VLh9PiMlhDzE6wbt26JGAJgIh8M3/+/FZJJWs2m+mVdx1/ezNIOHzgdMwvGuW6RnlUOMNu5dIkDXuDVcfWiI/OQ79mt7aVgqIdP1AQAA+89ttY7IQ5yI5dYXyrt7Pz7cn7D8MQ6w0Msd7Q7PuYPXs2Vqs1X0QK64+JiN/hcMycNOnAuIREE41GGTduHJ0tx+NwJFES2E6/3r9B65BCOMNGUmXMG05LgqhDxWJrbLF/dUvM7TrYMQnTmQOI9OtO1A7YdEyn9eEkx9msrp5OP2fTJrLLli1DKcUZjiGHbDffNZ5ibSfdz+rk9vv9/0vAx9A6JHYl8Qg/DGK7GRglIltEZDfwFnCDUsoO/Bb4q4jUisgEYiuBnzXjDqLA+0qpPUqp/yilzmxGH3F5NxXu3LmzfS4LE8jHH39MUlLSPBFpaKVfvGrVKkeiU28fl2OhvPIgmWYFksoCmEIRiArhDAtaMiSVQWqBmaRSE5aAItkZoqetgkHOAnLtNQSjFrxrVxOJhuiZG7+f/po1a3A4HCUiUlN3aH1JSYm1srKyZTfaCOv/9zKmjG68OLLmgHNRke+S5e5PRDSuWXUPSSqFsAQOiIYvLi7mtttup3v/X/JQZiED/5RD6gXnkpGR8V2by1Ju47KU21p8D2+//bbP5XKN2v+4y+V6Z+TIkYfOSNhCBpovwGa188DQp0g3d+DC3Ls459T7sXU9nlCmlXCaGTErzGGI2iGYCcEMRShdEU6NBWwisQJYoUwL4XQL5rpM4JEMRccTzuE058VsDizmgi63H1ae+oDTVaHZnGG7lMscNzXaNhwOs3r16iRidr/2h3wfkHq41+FQSvUBbgeGNzjcH1jb4P0moDfQB/CKSNFBzsV3CyJDRaQ3cAVQDbyhlNqplPpXPP3Es3VUWFxcbI+n86MNEeHll1/21NbWvrLf8arMzMy9K1as6HXuuec2dnncfO1KpZ+j9oDjxy2NYPKEwGJCy3bi72AmagVzBCyemNeT/8Qw2fYwqaYgvf1uXnpHWD61DP+enQzMuYrZK5+OW57Zs2frmqbNqH8vIlp2dvbyefPmXbB/xG+i+ParGZxwykk8OfSHTgE55hRyGjg9ufUAn3qP57WtP6PzCzaOL6tFkrPBF1MKvXr1+q7tz3/1V+x9e+C9sTs93ryRwLoXqdwvenyWd1yLZS8vL2f27NlmXdcPlof9f3v27AmtWbMmdeDAgS0e62Cs179BR6fL3fcjyRZKFFh8YPV+//CKpEAoE7QUHVPHEGZnCH/ABnuTyNoEVj2WfVe3Kuw1GjlrTQR3mRGzsO/kFJIzLiRpzhIWlr7HzzPNfFUzplF5UlNTKSoqom/3/tz39v9x++2NK5ZVq1aRlJS0JxgMHjhDaC8kYEqslDIB7wIPiYivQSBnGrFSovV46o7tf7zhuWYhIhvqtrtMwK3ALcQKEjWJeFYSleFw2FSfIfRYZMWKFZSWlgaAufufC4VC07/66quE+js4/C7S0374J3i0fADmQKy2hAqEsZbUklKmYfXFguuiDgjkQHq2l4BH44Z7HfQaVMWGySn0KMvhbMcVrChr3jbH1KlTvT6f74uGx2pra6fMmDGj1XL99+jRA4lE8XgP/dGaUJxiL+JnXbdj9gSRSJjyUAHwfXbTemz2VKIuLxIGz8x5pJ88qEWeaY3x7rvv6jabbcp+q04gVvBF07SRb7zxRqslrutk78kJva4gpcqM0iF0fAh/rk4osy6+Jhl0G7ENdiAlJUBaUhC7PRLzlLMqrJ4ozpIgqYX+WIxO3QxaNyt0i0JLMTO4/wMkmVLZE9p8SHkAcnNzcWvVh1QQAHPmzNHD4fBXh2zUxsSxkuiglFrV4HVPg27+COwUkf3rINcCSQ3eO4GagxxveC4++ZW6Sik1WilVBMwAcoC7gLx4+onHJiHJyclF27dvj0/So4jnn3/eHwqF/iUiBzyxAoHA1EmTJh0YytsCMnzaAUri08VnYIroscp1ug66kFTsw1Gr4+4tZP9mL49f+xnubensuXUSjuUa+0rLKduzkvXBBXzjn9LIaIempqaGDRs22IGvGx7Xdf2L6dOnN7vi2uFQSmHP68biFYfWQykmB2fYraSYQ0T0EIuK3qPAtYqBpgswm38YZ5GxNwTlbsqHPkdozQZO3dEt4XKHw2FeeumloNvtbnTpHgqF3pw4ceJ3WXUTjVk3kb/zCyIWjVC2jjIJkqYR7KQT6CL4uwj+LlEiXUKk96wlJ8VLeU0q4e3pZGxTZOQHsRfVYimrxVzuoj4iU8zgPw5qTxQqB5jZd1Y2Zxx3LTtD69ixY0dCZJ8wYYLX7/fHbxE/UsRXma5KRAY1eI1u0NOFwI1KqaBSqn7CUEhs++jkBu1OAtbXnctUSmUd5Fy8jCBmFL8B6CoiD4rIwni9yeLy1jGZTJu3bGmfEfQtZdeuXcyePVsikUhj6+nFu3fvNhcXJy4XWTgiOBw//BOk7DKjojpEIrEiRKJDVDDVGXedlggZZh/WVWX4rD72VK/7wV57c5k5cyYpKSlLReQHT2sR2SEi1atWrWrxGI2R2r0vE2d/v+0WkMZLZJ6ZUoA/6savu6nVq1gd/fqANnP3vk15RRHzvv4Kr1bD/H0fJlzm8ePHIyLrRaRRn3MRqbBarZPeeOMNLeECAKru5xv21Hy3WjA7NMQiiClmsMYUq/xnNumYlKBVO0gqg5TiCNZqHwSCse9aJBJLDUNdsOZ+nsnWnj1JTjsuIUpi9+7dFBYWmmmv9og6EmGTEJFrRMQuIg4RqXfjOx64EbhPKZWrlDoReBgYLyI+4HPgaaVUklLqTmKBRMvjlV9EuorIw8S2ry5RStmVUnF7p8alJNxu9+pNmzY1v6ZnO+bZZ58NAiNF5KDGRhHR7Hb7zMmTD/SQaS6fbMvD2SCD3a93DCEzX8PkC8Uq1IXC4A9g8ocwRwRTBAZn7yQiFqJV1diTsw6YRTeXjz76yNfQ7bch4XB4wqSo/ymzAAAgAElEQVRJk1qtYHY380l8OjXKlh1BqvVDL9ayTF5qvXs4Lrv/IRP1ZWZmMnjw4FZJ5qdpGsOHD/fV1tYe1qXQ4/E89+qrr0b2z1aQCHaHNpOV3ovagvWxtCQRE9GwGRyxn6jSwew3oaptVFemsWdfJuasECatrhaJFgusIxyGYAhLhRtbbRibV0gugtTdCmcZmINCIMcODjuP3XWAjT5upk6dis1mmyEiraI8E0VrpuUQka+A94ENxJTlGyLfVZJ6CPgJsI9Ylbnfikjcz12l1ClKqR3ElM4MoC+wSyl1ejz9xKUkNE3bvHbt2oRuubQHCgsL+fjjj/VAIPDCodq5XK5x7733XsKMMtkV+ZzeP+YL4NYDlI/qiaMiNosWnx8J1bnHRjTslSHSChSj513MnyYNoWjBp/TIaJZH2wF4vV7mzp1rqfPRPoBgMDjhgw8+CLdWzNOqOS+Q1+FSzrzPyt/Lz8dyiDQd1719PjuLv6abNfGR001l4sSJeDye7cD8w7UVkXyTyfTFq6++mvDJlVKKpSu+pHL9QqJ7qzHVWDHts2FyWVG6Im2nImOrInODiexvbCR9lUbGXCcZuzQs3jqdbzaBxQKWWGVDS7Wf1HwXHVfU0nmxm4wdEXy5iqpTzeihIHqHJicPbZQPP/zQ7Xa7m150va1IcDAdgIgoESmr+/9zIpIlIjki8nKDNuUiMkREkkRkgIisa+YdjAZeEpEegF7Xz+PA2/F0Em9w2KYNGza0WurotmLYsGEBpdQbIlJ9mKb/27x5s2Xv3r0JGTcjzYTbE1uvDvn2lu+W+8B3+8MoBVYLmBSmiNBxmRB4ZTJdup/D+k2J2UaZNm0aTqdzpYjsa6TJOr/f716x4oDU9Alj0+bJaHtcfPGlCWsjK+LySo2qEZ/R5brfsax0/1oqR4ZwOMyjjz7qd7lcf2rq3q7b7R724osvRqqrD/f1ip8+ffqQa+1N5MvlmMIKU0hhCiqsboUoSKqK4qzUSNsdJmObn5QttZg9scmHnmRFUp2QlgIZaUiSLVbPRNdRug66Tm0vK7oFIkEvPk8p2ZkntEje4uJiNm7caAUSn4o3gTR1FdHOE/z1A+rd+OolnURsldJk4n3gb6uqqrJ7PK3q/n1EWb9+PdOmTYv4/f7nD9dWREJWq/XTDz/8MCFW3GSnwuMVPvJkkWwLUfWbAPtOTo6VNAWU1QJOJ7rTjpgVyXtD7J36DlK1j16FmYkQAYC3337bU1NT82Zj50VEwuHw6LFjxzZuLGghVquVPpnnUTR26UHPl5Zr9Pill8wrB1I4oVFRW5233npL9/v9q0TksKuIeupWExOeeeaZuCJmm0pPyylU5S/DurUmViI9GvOEswQFaj1Ub17K9hXjWbToORYv/icrlr/GjpKv8XW04uuVQeD4TMLHpRHqlEI4J5lIh2Qi2U60NAeuE3XCmYJv4wZsPXvy9fxmBe1+x7hx43Sr1frp/ravdkkrrCSOMMuIBe015FJgYzydxJsqXEtJSdn17bfHRtJGEeH+++/3RSKRp0SkSdtIHo9n9KhRo/yJ2Hrp0tlCWaXGTan7KK7JwGzWY4n8NO27cqbhiBel65i9ISrmTcbvr6LEv5s5kcTMpIuLi1mxYoUFOGQOj1AoNO6jjz6SUKjV9AQvvHkPWkkscM/ljjJ/sZ9ZX3vJeTiXXmdVk2s+jYrxTX42J5x9+/bx1FNPhVwu1/3xXuvxeJ4YM2aMlijvoIbYNQt2ayrh4iKcJWDf7sW0ZAfRZetZMv/vVBQsJ9VtpnDPTiLREDNmfkJJ6Uq2r5nI7k1fsXbZSHSLCUdBFfZiN6awjpZsoegiB0pTWOfvpmb6dE6t7NsiOUWEN998M+DxeN5K0K23KokKpmtD7gHuV0ptAGxKqaXA63XHm0zclu5oNLpi7dq1fRIZVNZWTJkyhfXr11dGIpF4pqZLampqXEuWLElpyWfw88y72JsT4YQeMTcSLWRGROFssEgLht18XTWBtIocMpPyKNE2MoiLcDgSl0rp3XffjdpstknBYPCQKVdEZFdmZuaGqVOnntFagXWDBg0iGvCSMSSEv6AcS+ccxKeTHijh1B7XsnxL44FcR4Jhw4aFRGSiiBw6//VBEJFyh8Px93vvvfevc+bMcSZSrq/cY7FYHFRvWopWUcHeDV+R6uyMHgrRJ+unbK3+Yd3pCy+8kLKKPWRmZkJlrD62rmsxT6dwBLNZQboVFJg0KFs4jZ6nXsWStRPjkuvqq6/mgQce4OKLLwZgyZIluN3uWuKssdxmtO9VwmERkUKl1GnAGUB3Yvmglokcwn3wIMRtX3C73UuWL1/e/peKh8Hv9/OHP/zB7/F47hCRJnvuiIgEAoHXRowY0aLPYOKul9hTHOGUvjHDtWNjEhlLHHRaVff3UwpryESW6oQ7XIHyhzgj6ec/KGLfUqLRKCNHjgx6PJ7Xm9K+trb2P6+++mqr7TV27NiR8zrfSm55Hy5IvYWLglcTKi2honZbmyuIdevW8cEHH4Q9Hs+fm9tHKBT6z/Lly2umT5+eSNEAON98JZl0JFxQwJm5N+DyFOEJVx6gIOrJyMhgUPLlmOvyYRWumwamOnuEx48pIogC37YtaEEfec74a7xPmzaNSy65hCGO2I7HqFGjgsFgcES7zfrakASm5TjS1GWXfVQp9SjwF2KxGj2As4CH6o43meZkdF29bNmyCAdGBR5VPPnkk+FgMDgrnr3lejRNGzt16tRnW1KU5ae9fku3XCsWS8xFM9hJyNqmYw5oSHoKpKdgrvXQrbgPAc3HrnBc24hNYubMmYRCoSIRaWo+8Knr168fvWXLFvr2bdnWQ2MsLG15uoxEE41Gufnmm33hcPiRQxj3D4uIhJVSt915552f79y505mamrjU+/NC8UfZr/R+yaWmawngY1n1HLqfexlmZwoRm07RdRDdU4N/5kI6nnYhcxYPP3yH+3GcOp5SKSSfb1m2bBmfffaZikQi78XdURvRzo3Sh+JwP8647qw5SuLb3bt3O4PBYEK3PY4kq1evZvTo0SG/339vc64Xkar09PSpY8aMue6JJ55olreXIOwKfl81zupWmOpqS/h0Fy5vEWFvNXu0tRxvaZ0H8osvvuh1u92HNdjXIyIhp9P55muvvTZ01KhRx3Qer4a89tpr+t69ezdrmvZuS/sSkbnp6enTH3/88V+PHDkyvjS9rcBsPaZculv7smL1G6Rk5FFdtgnHjq6E91aTYT2ObpGecfc75IQ/ETZHQIPC0AYuOe8K7Cn2eX6/vyzR99BatMdVQlMQkQNyoiilbPGmGq8n7geciASTk5P3HK3Ga13XueOOO3yhUOhhEWl2vgS32/3Sq6++Gmhuuoq0Tr2JBGrR0RlW0Z+0XbH0G5ZqL+V7V7Nh12QC3kqmzvqMTeG4gy0PS0FBAStXrkREPonnukAgMOL999/H5zvmwmUOSmlpKcOHDw+73e6bE7VN4na7/zh27NjQ+vXtp7Tz7sgWVq9azF8evoVXXnmF9J1mzrNfTXXtDhau/Hdcfem6TsG+ZVRrxaR37oMtOYsOuam+2tralw9/dTshvrQc7RKlVIZS6l2l1D7Ao5QaoJT6RCnVIZ5+mjcLFlnWmmkaWpPx48dTWFi4JxqNvtfCrtaEQqHyr7/+ulkXh1QIS6cMVoR0rstYQejXtZQOcrKi4AP2utbRw3oKu4ObGDJkSKtEDf/3v//VTCbThyISVwI6ESm22+3LP/us/abdSSSPPvpoUCn1togkLGmZiFRrmvbEvffe62tP2/P9+vXj/vvv50+P/JmICrPOM4d45fP5fJjNZnbuWwKA7vXy1fRPqa6u9gDzWkHs1uMoVxLAKGLP+IGATsz1tYJYVtom0ywl4XK5Fi1duvSoM16Hw2GGDh3qd7vddx8siV88iIh4vd43Ro8e3axCTDpRght3smCBRl+rmX4dy4jadPZpJQTFR3ct7vTxTUZEGD16dMjn8zUrx0Jtbe0bo0aNOnaCZRph48aNTJ48Oezz+Z5KdN+RSOTtzZs3V3755ZeJ7rpFxLaQFXZnJi4tvoX2zy78B11PGvzd+1RzRwY5LuG9994LhEKh11v6mzuS1FemOxoN1w34BbEU5YXEHlkR4DHiLGDU3OjpjevWrWuVwKDW5KOPPiISiawXkcWJ6C8ajX46Y8YMc3OKET39j1iZ2a1rA5hQaLoZU51jUw/Vl/l64nJE7c/atWsJBoMe4iyI3oAv16xZY9u3r9k23KOCZ5991h+NRl9oagxNPIiI5vF4Hh8+fHhCKx62FLPZTOfjz6LUtYmk1E5NXsXm/ukh1qx9h5o9sa/UCRffiVurYFbJGCZPnqwikUj7T8OxH0qkSa92zC4ONGJ3Bcrj6aS5SmLLjh07ktrTUvlwRKNRnn76aa/L5WpZyGgDRKTIarXuXrhwYdzXWq0x18POJ2WwNRJh5aqeVM+ZgdOcRoF++Lz9LWHy5MnRaDT6cXP32EXE73Q6F82YMePwjY9SCgsLmT59OqFQaERrjSEin+Xn5/u++eab1hqiWfTzncRZmVfjc5U2qf0Jg66n/J2xyJnZWC1OTuh+OdvnxFyWFyxYgMViKRSRPa0pc8I5il1gG/AIME0p9QZgUUr9E5gJPBlPJ821SVQrpUKlpU37ErUHJk6cSG1t7S6akJQtHnw+37jx48fHXVjmwf97hvTe2VQPOJdXyy8h5bMCqnev5eSk8xMp3gGICOPGjQv4/f74IqP2o6amZty4ceOO2S2n4cOHB5VSIw5WUChRiIgWCAT++uijj7ar1cT/ykezbN+UJq0iLsv9IztWf4Ktdx6B5QV0GvIbthd+v4U2YcKEoNfrfa8VxW09jnKbhIjMBU4H9gLvAEHgShGJK11Ds5P1OZ3OHZs3t+6MN1FomsZjjz3mc7vdQxMdyBOJRCZ88sknxLvlFHREce2oJhk/y4u709GfhclspTDYul5j3377LbW1tUGakZ9+Pz5fvHjxMbnllJ+fz2effRYNBAJx1QJuDtFodNyGDRu88+e3XbqRljCreCQDT7qdnO02+lvPY+8X32ebj0ajfPrpp6JpWvNKJbYxx8BKAhEpFpEXROSPIvKMiMQdcNVsJREMBle1Jxe+Q/H222+L1+vdQCt4V4jILovFsnPWrFlxXWdNyST9VxeSk+QnxRHGJCaIaGRbuiRaxB/w3nvvRaLR6HstVZYi4k5KSpo3adJR+fsH4Djz8WSZOhEO/9C89sgjj/jrflitXn9ZRCI+n+9P999/v7e1qv+1Nqs3/ZdC7zpWVX/+g+OzZs3CZDLtFpGCNhKt+RwbWWATQrOVhM/nW7J06dJ2tUw+GLW1tQwbNizocrnuba10AC6X6/VRo0bFFTjwt7/eRLS8nN2BbGrWdmRrxVxSrFlsDnyfBVXXdQKBxDmRRSIRxo4dqwUCgYTkuKitrR05cuTIo3LLKRqNUqbvJig+TKbvfwaLFi1i/vz5/mAw+OKRkkVEJhYVFe0ZP378kRryiDBixAify+V6pa3laA7HiHdTQmhJbYg1y5cvb/d69MknnwwDk0Wk1ZY9IvLxnDlzzOXlTXcauOqqq/Au38LsDXl0/ypAyd6ldLZ+H9n64YcfYjabcTqdCasv/cUXX6CU2iEi2xLSIczauXNndOPGxKcMaW3MZjMigl+8WCyxxAOapnH33Xf7/H7/Q0cylbWI6G63++6HHnrI73Yn3JGqTSgrK2P+/PkmEZnQ1rI0G5GmvY5xWqIktpSXlzu83va7mFi9ejVjx44Nud3uh1tzHBFx2e32Ke+++26Tn+ZZWVnkZQ6k8I7nWb4sFohaHPz+2W21WnGQTF91+g9mui3h5Zdf9rpcrkNW34sHEdF0XX9zxIgRrZc//Ajy+uuv66WlpRvb4sEmIksikciUJ5544pj4LMeOHavbbLYpjZUDbvccG95NCUG1ZAcmOzt7y5QpU35y/vmt65HTHCKRCP379/fl5+c/qGnaf1t7PKXU6R06dFhYUlLirHdvPRwFBQX06tULgOzUnlR7CnCoZAaZLmSRFp976WXJtwIwy/f+Qc9v27aNAQMGeAKBQE68UdaHQimV53Q680tKShzp6S0vbdlWFBQUcMoppwT8fv+ABK604kIplZ2UlFQwb968tLPPPrstREgImqaRm5vrr6io+JmIJD6nzBEgJaur9L+0aXPLpZ/8ebWIDGplkdqMFk1Rg8HgnEWLFrXL9dazzz6rlZSUrIpGo2OPxHgislrTtK2ffvppk6/p2bMnPp+PXqln4gtUARAUX7O86mb53m9UQQD8+9//DhIrtp4wBQGxWBGLxfLV6NGjj9o5la7r3HjjjT5d159pKwUBMdfyUCh053XXXef3+5sVyN8u+PjjjwmFQluPVgXxHUe5C2yiaJGS8Pv9c2fNmtXulpPLly/n5ZdfDrjd7v87krnra2tr//b000974xnS6XSyw70cX6gGn8+HiPBNnKuIw1FWVsbEiRMlEAi8ltCO63C73c/+61//CrZm1brW5KWXXopu3bo1PxgMvtTWskSj0U9dLtf/hg4delR+mLquM3z4cK/L5RrW1rK0CAGlS5Nexzot3exevGrVKkc0Gk2IMIlg3759/OpXv/IHg8FbRaTkCA//RVlZWVlzisqYTCaczoQWLPuO559/Pmw2m8e1JOvtoRCRtbqurxwzZsxR94tZunQpzzzzjN/tdl8tIu3ii+x2u3/30Ucf1RyN7sUzZsygurq6BPhfW8vSUgwX2BgtUhIiUmmz2SrWrl2bKHlaRDQa5frrr/f7fL73o9Ho1CM9fl3Sv7/8+c9/9rUXn/fi4mLGjBkT9Xq9z7bmOLW1tX956qmngol02W1tysvLueqqq/zBYPAWEdnd1vLUIyIun8935e233x7YsmVLW4vTZHRd5/HHH/d6vd4nj4rqc4fAcIH9nha7zWia9vnMmTPbxUf12GOPhZcvX77R5/M92FYy6Lo+rby8fNdHH7U8n9kQ6w0Msd7Qoj4ef/zxoFJqlIi0ag4VEVmpadqCl19+uV3Mxg9HKBTi8ssv9/n9/tei0ei0tpZnf0RkVSQSefDSSy/1Hy1R7ePGjaO4uHiXrutHfx75prq/Ht26sEm0WEn4fL6pkyZNanM/2NGjR8uoUaP2eTyeX8RTszrRiIi43e57hw4d6m+Je3BxcTHrootYE13Azzv8vll9rF27ls8++yzi9/ufabYgceB2ux/85z//GW7vOb10Xefmm28O7ty5c6HP50tYwsdEEwqFxrhcrrFXXHGFPxhMqL9BwnG73TzyyCMBt9t959G+iqjHWEnESIQD/sLt27fbqqqqEtBV85g8eTJDhw51+Xy+80Wkus0EqUNEFkcikS+feuqpuNOpiwjH9RxMXl4elVKC3ZbarKJDuq5z2223+SKRyNDWTFLXEBHJB9564IEHjvie089OeZSfnnT/YQMPRYQHHnggPGvWrM1ut/ua9l7jwOv1PrRp06a511xzTeBQtr/Luz3M4F53sXv397tmlw56isMF502fPp2Kipabqp5++umIruvTRGRliztrJxg2iRgtipOoJysra/Z//vOfS26//YDSqq3O9OnTueGGG7x+v/8CEVlzxAVoBKVUp6SkpB2LFi1KOf3005t0zZCBT7G25kuqClcDMODO/7BmzCPNGv/111/Xhw8f/q3b7T79SD4IlVLJycnJBZMmTcq5/PLLW3Ws8y5+Bs/OjWxLXY+2eQ+aHiajZ39OHHAjlr3VOOzpzFn4fVZkEeGxxx6LvPXWW3u8Xu8gEaltVQEThFLKnpaWNveyyy47fZ0vx1GubcD9v4XkXXIDymxG7BYyFhWzsWYOZmUl9aQBWOxOatYtRkTIyfwJ+qWnYFqxi5DfBQihTBMRdzWRknJsWTlk5vVDM2ukbffSNakfCyo/OKxc9axevZrzzjvPFwgEeovIUVPD+lCkpufJwHObtmu9cOZjh4yTUErdBjwDdABWA/cA24H/AHcCPuBZERlV174H8AGxDK7fAr8TkTYzTiVESSilrj377LPfXbp0aWoCZGoykydP5pZbbvH4/f5LRGTFkRy7KVgslpu7des2avPmzcmxil+No+s6Z/7kd6zOj/048+56gL3vvN6scbdv386AAQP8fr//tLrZ/RFFKXVRVlbWjPz8fGdWVlaL+9M0jZOTz+G/81+je/funPzgPfykbA7Ll0ax9erGv271cP0tNs59+TZKP/gvYU8N6Dq6aJzZ+TqWl37MSb94mB0bPsbqC+z117gGikjbLX2bgVLKmZKVudjv9p9mO7k3HR37GNzZg66Dx6tjtyl+9lMnN/46lbET3az1Wbn58gi/X38Xkfn5+It20uUnGg/9rIiFgRP4qT2fn/ZJIyvDxMfTvCzwpLN67cmEFq/Eo1XT+cTzSAskkezowIqtjceiejwe+vbt6y8rK7tT07QWpZ9vT6Sm58npg5umJBZ81biSUEqdAKwFrgW+Bh4GrgNGAA8BlwNZxEoYXCoia5VSi4CFwL+B3wM3ichpLbqhFpAoJeFwOBzV+fn5zry8vASIdXhGjBihP/bYYx6/3/+z9rSCaIhSSqWlpX1+7bXXXjpmzBh7Y+0uc9xEVXcza7Z/gLKYSD/jXHz52xh07lCWTH08rjEDgQADBgzw7dq16/HWLJhzOFJTU0cOHjz4dzNnznTWpxUREWpqaqhXHFVVVZx/yk3s00pxOLNwufZgjoLZZCWTjlhMdmqzNWqKNkI4QsgURtdDnPrr7tz5czd3XJqFw/HDHVNNEzZuDTP49xqhghIy7F3wpIaQGhcpadaguybQ9WhTEPUopRw9T8rafHx2oMenY44jPc2c0P5rdD8DP3sI69xCglu3Ei4vxuUrRiwmTuhxOabOHZkz/q906tTpu2tuuumm4PTp0ye73e6bEipMG5Oanienn/NAk9oumPX4oZTE74FfisiVde+tQAhYALwrIh/WHX+D2IriTWAzkC0iIaWUCdgHnC0iW1t4W80iIUmBRCRos9mmfPDBB626rRGJRDjVcT7pjs488diT1X6/f2B7VRDwnRH7pokTPvGk2nLonXUOEMtM29BVNCJh1myPrSBE03nz1nySSKG6eEO843H33XeHSktL54TD4ZGJu5P48Xq9Q5cuXbrj+eef1wBO63IVJpOJ7OxsbLZklFJ06p5Hta8QmzUFj6eEzIyedM0aSE7aidSGy6kNl2E220j9003ct3oII9cOZO/aHqweaeO+KzscoCAALBbFmb+uIFQQC5F56IEgA/K8nNbPnu+uCWQfrQoCYr+zgs37+lRWmb8471dFFOxOrH9GpsnJrmvfYfuo2ez5ei9lW3T8uzuT99NfU1q6isJ10+jcuTM9zvwtAO+//z6ff/55lcfjuSehgrQHEpe7aSrQUNucDviB/sRWGPVsAnoDpwJbRCQEseSPwNa6c21CQlYSAEqpQdnZ2QtKSkqcNputyddVV1ezdetWbDYb9/5uFGs2/5cU53F4/WWckHUu9qCJXHsfZlS8RZI1BY0QDluqOxj2HH8k8v0nAqVUP2AjQErH4/FWFgKQntoViUaJ6hFE0/BrNSiLiY/fyuGeCf2I+v24ly5p8jjPPfec9sILL+zyer0DRaTNPc6UUrnJycnrOzsHZO+s/IbM/7uSj25YSn56LkGfzgMn+bHbE5O8sJ7e83+HfD6ZW3N3cdZAO7//SyWZ6Ukfbtjiua29G6mbilJKdctLGhYIhP/+5r9z+M0VKa0+5ppvg1z5ajpVC/ewbME8SktLuf766z1+v/9cEYlvNnMUkJaWJ4POur9JbefPeWI30HDyMVpERu/fTil1DTCKmH3iFaCHiBTVnbsJuA0YB9wuIpc0uG42MFZE2iSXvCVRHYnIqszMzPUffvjhOXfccUej7YY4bmZz9xKiSRuozRfCmhdL546Ahm2fwmy2EwhWY7UkUVCzjKho5AdW47CNI0qE5PTst32u6vuOph+8iGxSSl1scjjmZvzmBG66oAtndq3m3wtOo3qrC6spjQx28ceLdnNSkoUZs324v1lMt1/ccsh+dV2n+1N/pUv2FpKXLmL1bL/P6w1c0B4UBMSqYimlLtoTXbUeUJuf2EhOh0wuoz4vUWIVBMCOi94jeI7OP14V7ni4gsrq6C/2FrtnJnygNqTOxfQfSqnZf/pb1dJZ832mF57qkPDtJ4BwWHhgWAXvzRSG3X87f3zvj3z77bdcf/31vjpb4DGnIOpR0SZPoKsOY7juALxLbBVxp4h8rpT6G5DUoJkTqAFq9zve8FybkLCVBIBS6oLc3NwvCgsLk+tz9NfU1DBv3jyu/e21pCfnEfG7CFk1zv3LKbz18zKO72o56GzyA08Hnl5xJaHtNeyb+CkW9z7NV+a6RkQ+P6DxUYLJZLoiI9M047N3OnPB4FgKji/8Dp7d9kvW3jSSaI0bpaDjGZdygpzKNytidW/8fj/n9r+TJN3JkoJ3OaPvney1FeKpXEkobMZuF3SXV4K+aO/2WAVMKXV2ZoZp6dsv5nDNL1vXt2HBEj/3PVZBZoa9cOkq7+DWDiJsa5RS6aednPppZXXgklef68ivf5HcLJfpxuj9TC5lX37L4MDVzKl4lwULFnDFFVf4fT7f5SKyMGEDtTPSUvPkjEF/bFLbeV8PO5RNIpmYR9MS4MH6CVydcfplEZlS9/4VoBL4BFgBdBARvc4mUQGcKiLFLbytZpFoJaHS0tK+6ejuOriH6gtAkWU3WyPfu05bO3bk8RkDebrboZ9llVUa/3i1ho8mu+mYnfTGth2+P4tI3HEH7Q2zWV2cnWme88yj2fz+1lhq7b6j/4Dvtfcp3reO/mkXkxPMoSScj6CTmdGDDbICj2svyfYO9OtyOSt2xewX97x/FvqsLSxYGtTyC8K9RGRPW4KrXyAAAAdbSURBVN7boVBKDcztbFn9+1vTeeKhTEymxD3IADZsCTHs+So2bglLUYl2bVSXoz/qNw6UUhf27WObk5luMv/zyQ789Kz9J6PxEQzq3D+skrET3KRaOjA46xryK76hiB1opsil0Wh0ToJEb5ekpebKmQObpiTmLnzyUEriHuBGEblov+P3ArcAVwInANOBc0UkXym1DPgUGAk8ClwkIhc2915aSkKVBMTqC9iw7z2Nc0lTWYjVRLm5hI2Bb75rk/fkMM6/soIPui844PpN20K8OdbFx9M8nHxi8sJFyz3XiUjTS74dBSil+pzY27al/0k206vPdaRzjoUBT96B57PJVHryCekBIsSSgCabM/BFazGb7FjFQlBiVVI79k6hiyNMcpK1aMlK30lHQ3EXpVSX0091FGSmm+xv/rsjvY5vuu3qYOi6MGehn5FjXaxYE8RmszxVVBJ6od7o92NDKWVOdppu65BlerdHNyt/uD2dqy5LwWqNXyE/+mwlr78b4SznFei1bjazEixSUavtO71+H/1YJi01V84ccF+T2s5d9NdDKYkRwH3A/tvjvYgpgFuJbTE9Vm9zUEr1IRYn0R9YCbRpbrGEKwmA/ups2cparNjJIJsO5jy+jcaURO6l12O56gyyetRwf++v+V1aBfkFYb6c42PqTB/5u8KkpdpHbdvhf64NsrgeMZRSztNOThlTVBK48aG7M7jnlnSGBc5jzsqTSZtXg/p6LVt9SzD36UpK3oncPGg+V53mxGwS3p/kYdpXPjxeuTMQ1MceTWkQlFLW7l2TnvF6Q0/cdVM6992eTl6XphVpAohGhRVrg8yc6+eTzz047Eryd2n3BYP6ByISV53xYxWllE0pfn3mgKRxRaUR+3W/SuEXlyTz0zOTsNmapjCuntGT6XfPIolkNDSsNsvf/GHf348mW2BLSEvJlbNO/UOT2s5ZMvyYLjrUKkoCQCn1sNnpeMWmUrGHzYRNEfyhapJOOZl+l2cwJLyJohKNJSuD+AM6g05z7vn8K8+DwMxjYVupqSilTvrlpalffrPC133IhU5O62fH2tOMq1tvnjihnPxdETZtC7Nle5ilqwNs2BymRzfH+OVrfA8dze6cSqnjLzk/dfzqb33nnHdWEoNOdXDSiTZO6mOjZ3cr1TVR9pZoFNW/SjV27YmwYEmA4zqZSU2xTluy0vcvYPnRpCSPNEqpU/r9JOmPziT999t3Rjjv7CR6H2+laxcLuV0sdO1iIe84Cx2yzKzZEGLuIj9zF/pZsyFEj25Wyqv0cZVV2r/ayke/rUhLyZWz+jdRSSw1lETzO1fKPuRC5yvrNob+EAxJ7It5nEVyj7PoS1YGRm/bEVkNrAHW/dh/6EqpjsCVN/829cnK6miPzdvCqrRCo/fxVn5ygk1qXPqUBUsC44EvJMHV5doSpVQ6cOVvf5nyUCCon74lP6J2F0XIzjSTe5yFvC4Wyck2+/87wf13EfYA37Rn20t7RimVA1ygFN1vvzHt8X010aziMk0VlWiUV0Y5pa+dc890uN4c67qe2Of8o12ZpaXkytmn3NuktrOXPWUoiRYPopT6sSuB5qCUMv1YlvcN+bHed1ti/EZ/SFpyrpzdr2nZl2ev/NsxrSQSFidxKIwvX/P4sT4of6z33ZYYv9EfohCU8ZEAR0hJGBgYGBx1tJPqkm2NoSQMDAwM9kc40Gn1R4qhJAwMDAwOgjJWEoChJAwMDAwOwo+jfnVTMJSEgYGBwf4I0PQEf8c0hpIwMDAwOAiGd1MMQ0kYGBgY7I8AUcMmAYaSMDAwMDgIhk2iHkNJGBgYGBwMQ0kAhpIwMDAwOBBju+k7DCVhYGBgcAACRnYYwFASBgYGBgdirCS+w1ASBgYGBgfDsEkAhpIwMDAwOAhiJPirw1ASBgYGBvsjGEqiDkNJGBgYGBwMQ0kAhpIwMDAwOAgCumGTAENJGBgYGByIgFEgMYahJAwMDAwOhuECCxhKwsDAwOBAxPBuqsdQEgYGBgYHQaLRthahXWBqawEMDAwM2h91WWCb8joMSqnLlFL5SimfUuoTpVTqEbiBhGEoCQMDA4P9ESAabdrrECilMoEJwF+APEABz7W6/AnEUBIGBgYG+yGA6NKk12H4FbBGRKaKSA3wL+CG1pY/kRg2CQMDA4P9EUmUTaI/sLbB+41AJ6VUioh4EzFAa2MoCQMDA4P98FAza47+SYcmNncopVY1eD9aREbX/T8N2F1/QkRCSimt7rihJAwMDAyORkTk5wnqqhZIqn+jlLIRe+7WJKj/VsewSRgYGBi0HluBkxu87wvki0igjeSJG0NJGBgYGLQeU4HzlFLn1Xk6PQ+Mb2OZ4sJQEgYGBgathIhUA7cB7wN7gQrgn20qVJwoMaovGRgYGBg0grGSMDAwMDBoFENJGBgYGBg0iqEkDAwMDAwaxVASBgYGBgaNYigJAwMDA4NGMZSEgYGBgUGjGErCwMDAwKBRDCVhYGBgYNAohpIwMDAwMGiU/wfxveHswZBnDQAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
"source": [
"map_proj = cartopy.crs.InterruptedGoodeHomolosine()\n",
"data_proj = cartopy.crs.PlateCarree()\n",
@@ -382,13 +393,6 @@
"\n",
"fig.savefig('../figures/pcolormesh/pcolormesh_correct_homolosine.png', dpi=300, bbox_inches='tight', transparent=True)"
]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {},
- "outputs": [],
- "source": []
}
],
"metadata": {
diff --git a/jupyter/USGS-gtopo30_0.9x1.25_remap_c051027.nc b/nc-data/USGS-gtopo30_0.9x1.25_remap_c051027.nc
similarity index 100%
rename from jupyter/USGS-gtopo30_0.9x1.25_remap_c051027.nc
rename to nc-data/USGS-gtopo30_0.9x1.25_remap_c051027.nc