MMOE是2018年谷歌提出的,全称是Multi-gate Mixture-of-Experts, 对于多个优化任务,引入了多个专家进行不同的决策和组合,最终完成多目标的预测。解决的是硬共享里面如果多个任务相似性不是很强,底层的embedding学习反而相互影响,最终都学不好的痛点。
本篇文章首先是先了解下Hard-parameter sharing以及存在的问题,然后引出MMOE,对理论部分进行整理,最后是参考deepctr简单复现。
推荐系统中,即使同一个场景,常常也不只有一个业务目标。 在Youtube的视频推荐中,推荐排序任务不仅需要考虑到用户点击率,完播率,也需要考虑到一些满意度指标,例如,对视频是否喜欢,用户观看后对视频的评分;在淘宝的信息流商品推荐中,需要考虑到点击率,也需要考虑转化率;而在一些内容场景中,需要考虑到点击和互动、关注、停留时长等指标。
模型中,如果采用一个网络同时完成多个任务,就可以把这样的网络模型称为多任务模型, 这种模型能在不同任务之间学习共性以及差异性,能够提高建模的质量以及效率。 常见的多任务模型的设计范式大致可以分为三大类:
-
hard parameter sharing 方法: 这是非常经典的一种方式,底层是共享的隐藏层,学习各个任务的共同模式,上层用一些特定的全连接层学习特定任务模式。
这种方法目前用的也有,比如美团的猜你喜欢,知乎推荐的Ranking等, 这种方法最大的优势是Task越多, 单任务更加不可能过拟合,即可以减少任务之间过拟合的风险。 但是劣势也非常明显,就是底层强制的shared layers难以学习到适用于所有任务的有效表达。 **尤其是任务之间存在冲突的时候**。MMOE中给出了实验结论,当两个任务相关性没那么好(比如排序中的点击率与互动,点击与停留时长),此时这种结果会遭受训练困境,毕竟所有任务底层用的是同一组参数。 -
soft parameter sharing: 硬的不行,那就来软的,这个范式对应的结果从
MOE->MMOE->PLE等。 即底层不是使用共享的一个shared bottom,而是有多个tower, 称为多个专家,然后往往再有一个gating networks在多任务学习时,给不同的tower分配不同的权重,那么这样对于不同的任务,可以允许使用底层不同的专家组合去进行预测,相较于上面所有任务共享底层,这个方式显得更加灵活 -
任务序列依赖关系建模:这种适合于不同任务之间有一定的序列依赖关系。比如电商场景里面的ctr和cvr,其中cvr这个行为只有在点击之后才会发生。所以这种依赖关系如果能加以利用,可以解决任务预估中的样本选择偏差(SSB)和数据稀疏性(DS)问题
- 样本选择偏差: 后一阶段的模型基于上一阶段采样后的样本子集训练,但最终在全样本空间进行推理,带来严重泛化性问题
- 样本稀疏: 后一阶段的模型训练样本远小于前一阶段任务
ESSM是一种较为通用的任务序列依赖关系建模的方法,除此之外,阿里的DBMTL,ESSM2等工作都属于这一个范式。 这个范式可能后面会进行整理,本篇文章不过多赘述。
通过上面的描述,能大体上对多任务模型方面的几种常用建模范式有了解,然后也知道了hard parameter sharing存在的一些问题,即不能很好的权衡特定任务的目标与任务之间的冲突关系。而这也就是MMOE模型提出的一个动机所在了, 那么下面的关键就是MMOE模型是怎么建模任务之间的关系的,又是怎么能使得特定任务与任务关系保持平衡的?
带着这两个问题,下面看下MMOE的细节。
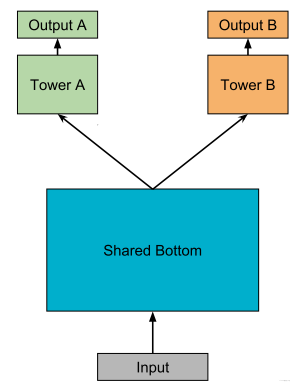
MMOE模型结构图如下。
这其实是一个演进的过程,首先hard parameter sharing这个就不用过多描述了, 下面主要是看MOE模型以及MMOE模型。
我们知道共享的这种模型结构,会遭受任务之间冲突而导致可能无法很好的收敛,从而无法学习到任务之间的共同模式。这个结构也可以看成是多个任务共用了一个专家。
先抛开任务关系, 我们发现一个专家在多任务学习上的表达能力很有限,于是乎,尝试引入多个专家,这就慢慢的演化出了混合专家模型。 公式表达如下: $$ y=\sum_{i=1}^{n} g(x){i} f{i}(x) $$ 这里的$y$表示的是多个专家的汇总输出,接下来这个东西要过特定的任务塔去得到特定任务的输出。 这里还加了一个门控网络机制,就是一个注意力网络, 来学习各个专家的重要性权重$\sum_{i=1}^{n} g(x)_{i}=1$。$f_i(x)$就是每个专家的输出, 而$g(x)_i$就是每个专家对应的权重。 虽然感觉这个东西,无非就是在单个专家的基础上多引入了几个全连接网络,然后又给这几个全连接网络加权,但是在我看来,这里面至少蕴含了好几个厉害的思路:
- 模型集成思想: 这个东西很像bagging的思路,即训练多个模型进行决策,这个决策的有效性显然要比单独一个模型来的靠谱一点,不管是从泛化能力,表达能力,学习能力上,应该都强于一个模型
- 注意力思想: 为了增加灵活性, 为不同的模型还学习了重要性权重,这可能考虑到了在学习任务的共性模式上, 不同的模型学习的模式不同,那么聚合的时候,显然不能按照相同的重要度聚合,所以为各个专家学习权重,默认了不同专家的决策地位不一样。这个思想目前不过也非常普遍了。
- multi-head机制: 从另一个角度看, 多个专家其实代表了多个不同head, 而不同的head代表了不同的非线性空间,之所以说表达能力增强了,是因为把输入特征映射到了不同的空间中去学习任务之间的共性模式。可以理解成从多个角度去捕捉任务之间的共性特征模式。
MOE使用了多个混合专家增加了各种表达能力,但是, 一个门控并不是很灵活,因为这所有的任务,最终只能选定一组专家组合,即这个专家组合是在多个任务上综合衡量的结果,并没有针对性了。 如果这些任务都比较相似,那就相当于用这一组专家组合确实可以应对这多个任务,学习到多个相似任务的共性。 但如果任务之间差的很大,这种单门控控制的方式就不行了,因为此时底层的多个专家学习到的特征模式相差可能会很大,毕竟任务不同,而单门控机制选择专家组合的时候,肯定是选择出那些有利于大多数任务的专家, 而对于某些特殊任务,可能学习的一塌糊涂。
所以,这种方式的缺口很明显,这样,也更能理解为啥提出多门控控制的专家混合模型了。
Multi-gate Mixture-of-Experts(MMOE)的魅力就在于在OMOE的基础上,对于每个任务都会涉及一个门控网络,这样,对于每个特定的任务,都能有一组对应的专家组合去进行预测。更关键的时候,参数量还不会增加太多。公式如下:
$$
y_{k}=h^{k}\left(f^{k}(x)\right),
$$
where $f^{k}(x)=\sum_{i=1}^{n} g^{k}(x){i} f{i}(x)$. 这里的$k$表示任务的个数。 每个门控网络是一个注意力网络:
$$
g^{k}(x)=\operatorname{softmax}\left(W_{g k} x\right)
$$
上面的公式这里不用过多解释。
这个改造看似很简单,只是在OMOE上额外多加了几个门控网络,但是却起到了杠杆般的效果,我这里分享下我的理解。
- 首先,就刚才分析的OMOE的问题,在专家组合选取上单门控会产生限制,此时如果多个任务产生了冲突,这种结构就无法进行很好的权衡。 而MMOE就不一样了。MMOE是针对每个任务都单独有个门控选择专家组合,那么即使任务冲突了,也能根据不同的门控进行调整,选择出对当前任务有帮助的专家组合。所以,我觉得单门控做到了针对所有任务在专家选择上的解耦,而多门控做到了针对各个任务在专家组合选择上的解耦。
- 多门控机制能够建模任务之间的关系了。如果各个任务都冲突, 那么此时有多门控的帮助, 此时让每个任务独享一个专家,如果任务之间能聚成几个相似的类,那么这几类之间应该对应的不同的专家组合,那么门控机制也可以选择出来。如果所有任务都相似,那这几个门控网络学习到的权重也会相似,所以这种机制把任务的无关,部分相关和全相关进行了一种统一。
- 灵活的参数共享, 这个我们可以和hard模式或者是针对每个任务单独建模的模型对比,对于hard模式,所有任务共享底层参数,而每个任务单独建模,是所有任务单独有一套参数,算是共享和不共享的两个极端,对于都共享的极端,害怕任务冲突,而对于一点都不共享的极端,无法利用迁移学习的优势,模型之间没法互享信息,互为补充,容易遭受过拟合的困境,另外还会增加计算量和参数量。 而MMOE处于两者的中间,既兼顾了如果有相似任务,那就参数共享,模式共享,互为补充,如果没有相似任务,那就独立学习,互不影响。 又把这两种极端给进行了统一。
- 训练时能快速收敛,这是因为相似的任务对于特定的专家组合训练都会产生贡献,这样进行一轮epoch,相当于单独任务训练时的多轮epoch。
OK, 到这里就把MMOE的故事整理完了,模型结构本身并不是很复杂,非常符合"大道至简"原理,简单且实用。
那么, 为什么多任务学习为什么是有效的呢? 这里整理一个看到比较不错的答案:
多任务学习有效的原因是引入了归纳偏置,两个效果:
- 互相促进: 可以把多任务模型之间的关系看作是互相先验知识,也称为归纳迁移,有了对模型的先验假设,可以更好提升模型的效果。解决数据稀疏性其实本身也是迁移学习的一个特性,多任务学习中也同样会体现
- 泛化作用:不同模型学到的表征不同,可能A模型学到的是B模型所没有学好的,B模型也有其自身的特点,而这一点很可能A学不好,这样一来模型健壮性更强
这里是MMOE模型的简单复现,参考的deepctr。
由于MMOE模型不是很复杂,所以这里就可以直接上代码,然后简单解释:
def MMOE(dnn_feature_columns, num_experts=3, expert_dnn_hidden_units=(256, 128), tower_dnn_hidden_units=(64,),
gate_dnn_hidden_units=(), l2_reg_embedding=0.00001, l2_reg_dnn=0, dnn_dropout=0, dnn_activation='relu',
dnn_use_bn=False, task_types=('binary', 'binary'), task_names=('ctr', 'ctcvr')):
num_tasks = len(task_names)
# 构建Input层并将Input层转成列表作为模型的输入
input_layer_dict = build_input_layers(dnn_feature_columns)
input_layers = list(input_layer_dict.values())
# 筛选出特征中的sparse和Dense特征, 后面要单独处理
sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), dnn_feature_columns))
dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), dnn_feature_columns))
# 获取Dense Input
dnn_dense_input = []
for fc in dense_feature_columns:
dnn_dense_input.append(input_layer_dict[fc.name])
# 构建embedding字典
embedding_layer_dict = build_embedding_layers(dnn_feature_columns)
# 离散的这些特特征embedding之后,然后拼接,然后直接作为全连接层Dense的输入,所以需要进行Flatten
dnn_sparse_embed_input = concat_embedding_list(sparse_feature_columns, input_layer_dict, embedding_layer_dict, flatten=False)
# 把连续特征和离散特征合并起来
dnn_input = combined_dnn_input(dnn_sparse_embed_input, dnn_dense_input)
# 建立专家层
expert_outputs = []
for i in range(num_experts):
expert_network = DNN(expert_dnn_hidden_units, dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, seed=2022, name='expert_'+str(i))(dnn_input)
expert_outputs.append(expert_network)
expert_concat = Lambda(lambda x: tf.stack(x, axis=1))(expert_outputs)
# 建立多门控机制层
mmoe_outputs = []
for i in range(num_tasks): # num_tasks=num_gates
# 建立门控层
gate_input = DNN(gate_dnn_hidden_units, dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, seed=2022, name='gate_'+task_names[i])(dnn_input)
gate_out = Dense(num_experts, use_bias=False, activation='softmax', name='gate_softmax_'+task_names[i])(gate_input)
gate_out = Lambda(lambda x: tf.expand_dims(x, axis=-1))(gate_out)
# gate multiply the expert
gate_mul_expert = Lambda(lambda x: reduce_sum(x[0] * x[1], axis=1, keep_dims=False), name='gate_mul_expert_'+task_names[i])([expert_concat, gate_out])
mmoe_outputs.append(gate_mul_expert)
# 每个任务独立的tower
task_outputs = []
for task_type, task_name, mmoe_out in zip(task_types, task_names, mmoe_outputs):
# 建立tower
tower_output = DNN(tower_dnn_hidden_units, dnn_activation, l2_reg_dnn, dnn_dropout, dnn_use_bn, seed=2022, name='tower_'+task_name)(mmoe_out)
logit = Dense(1, use_bias=False, activation=None)(tower_output)
output = PredictionLayer(task_type, name=task_name)(logit)
task_outputs.append(output)
model = Model(inputs=input_layers, outputs=task_outputs)
return model这个其实比较简单, 首先是传入封装好的dnn_features_columns, 这个是
dnn_features_columns = [SparseFeat(feat, feature_max_idx[feat], embedding_dim=4) for feat in sparse_features] \
+ [DenseFeat(feat, 1) for feat in dense_features]就是数据集先根据特征类别分成离散型特征和连续型特征,然后通过sparseFeat或者DenseFeat进行封装起来,组成的一个列表。
传入之后, 首先为这所有的特征列建立Input层,然后选择出离散特征和连续特征来,连续特征直接拼接即可, 而离散特征需要过embedding层得到连续型输入。把这个输入与连续特征拼接起来,就得到了送入专家的输入。
接下来,建立MMOE的多个专家, 这里的专家直接就是DNN,当然这个可以替换,比如MOSE里面就用了LSTM,这样的搭建模型方式非常灵活,替换起来非常简单。 把输入过多个专家得到的专家的输出,这里放到了列表里面。
接下来,建立多个门控网络,由于MMOE里面是每个任务会有一个单独的门控进行控制,所以这里的门控网络个数和任务数相同,门控网络也是DNN,接收输入,得到专家个输出作为每个专家的权重,把每个专家的输出加权组合得到门控网络最终的输出,放到列表中,这里的列表长度和task_num对应。
接下来, 为每个任务建立tower,学习特定的feature信息。同样也是DNN,接收的输入是上面列表的输出,每个任务的门控输出输入到各自的tower里面,得到最终的输出即可。 最终的输出也是个列表,对应的每个任务最终的网络输出值。
这就是整个MMOE网络的搭建逻辑。
参考资料: