comments

difficulty

edit_url

rating

source

2973. Find Number of Coins to Place in Tree Nodes

Description

You are given an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

You are also given a 0-indexed integer array cost of length n, where cost[i] is the cost assigned to the i^th node.

You need to place some coins on every node of the tree. The number of coins to be placed at node i can be calculated as:

If size of the subtree of node i is less than 3, place 1 coin.
Otherwise, place an amount of coins equal to the maximum product of cost values assigned to 3 distinct nodes in the subtree of node i. If this product is negative, place 0 coins.

Return an array coin of size n such that coin[i] is the number of coins placed at node i.

Example 1:

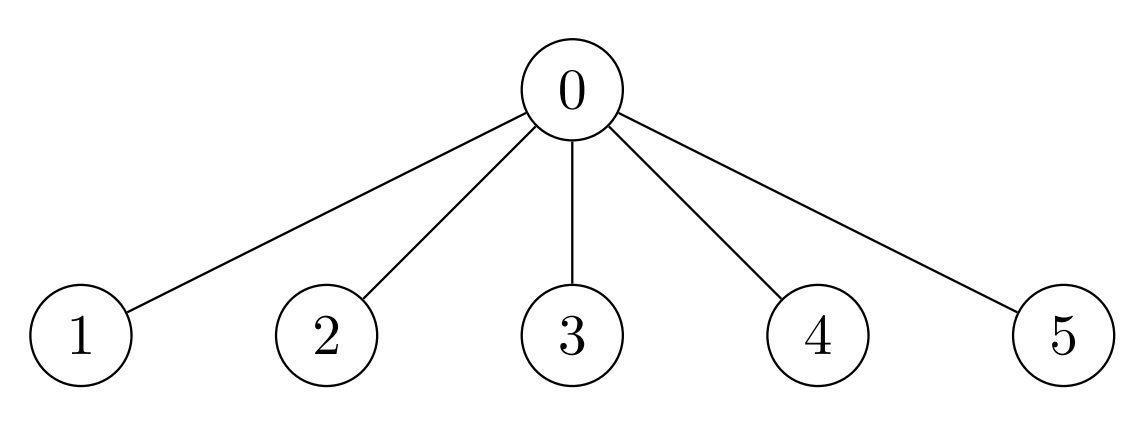
Input: edges = [[0,1],[0,2],[0,3],[0,4],[0,5]], cost = [1,2,3,4,5,6]
Output: [120,1,1,1,1,1]
Explanation: For node 0 place 6 * 5 * 4 = 120 coins. All other nodes are leaves with subtree of size 1, place 1 coin on each of them.

Example 2:

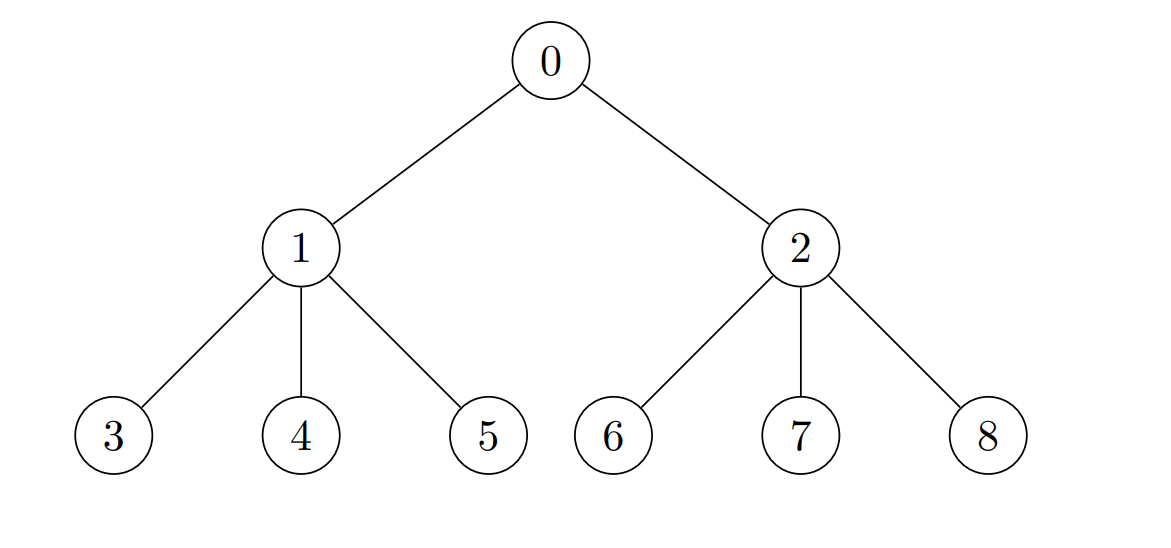
Input: edges = [[0,1],[0,2],[1,3],[1,4],[1,5],[2,6],[2,7],[2,8]], cost = [1,4,2,3,5,7,8,-4,2]
Output: [280,140,32,1,1,1,1,1,1]
Explanation: The coins placed on each node are:
- Place 8 * 7 * 5 = 280 coins on node 0.
- Place 7 * 5 * 4 = 140 coins on node 1.
- Place 8 * 2 * 2 = 32 coins on node 2.
- All other nodes are leaves with subtree of size 1, place 1 coin on each of them.

Example 3:

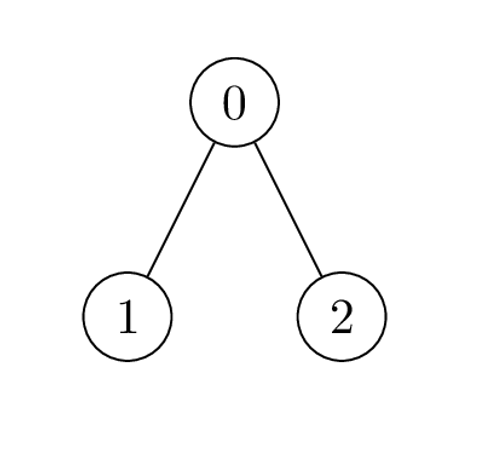
Input: edges = [[0,1],[0,2]], cost = [1,2,-2]
Output: [0,1,1]
Explanation: Node 1 and 2 are leaves with subtree of size 1, place 1 coin on each of them. For node 0 the only possible product of cost is 2 * 1 * -2 = -4. Hence place 0 coins on node 0.

Constraints:

2 <= n <= 2 * 10⁴
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
cost.length == n
1 <= |cost[i]| <= 10⁴
The input is generated such that edges represents a valid tree.

Solutions

Solution 1: DFS + Sorting

According to the problem description, there are two situations for the number of coins placed at each node $a$:

If the number of nodes in the subtree corresponding to node $a$ is less than $3$, then place $1$ coin;
If the number of nodes in the subtree corresponding to node $a$ is greater than or equal to $3$, then we need to take out $3$ different nodes from the subtree, calculate the maximum value of their cost product, and then place the corresponding number of coins at node $a$. If the maximum product is negative, place $0$ coins.

The first situation is relatively simple, we just need to count the number of nodes in the subtree of each node during the traversal.

For the second situation, if all costs are positive, we should take the $3$ nodes with the largest costs; if there are negative costs, we should take the $2$ nodes with the smallest costs and the $1$ node with the largest cost. Therefore, we need to maintain the smallest $2$ costs and the largest $3$ costs in each subtree.

We first construct the adjacency list $g$ based on the given two-dimensional array $edges$, where $g[a]$ represents all neighbor nodes of node $a$.

Next, we design a function $dfs(a, fa)$, which returns an array $res$, which stores the smallest $2$ costs and the largest $3$ costs in the subtree of node $a$ (may not be $5$).

In the function $dfs(a, fa)$, we add the cost $cost[a]$ of node $a$ to the array $res$, and then traverse all neighbor nodes $b$ of node $a$. If $b$ is not the parent node $fa$ of node $a$, then we add the result of $dfs(b, a)$ to the array $res$.

Then, we sort the array $res$, and then calculate the number of coins placed at node $a$ based on the length $m$ of the array $res$, and update $ans[a]$:

If $m \ge 3$, then the number of coins placed at node $a$ is $\max(0, res[m - 1] \times res[m - 2] \times res[m - 3], res[0] \times res[1] \times res[m - 1])$, otherwise the number of coins placed at node $a$ is $1$;
If $m > 5$, then we only need to keep the first $2$ elements and the last $3$ elements of the array $res$.

Finally, we call the function $dfs(0, -1)$, and return the answer array $ans$.

The time complexity is $O(n \times \log n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes.

Python3

class Solution:
    def placedCoins(self, edges: List[List[int]], cost: List[int]) -> List[int]:
        def dfs(a: int, fa: int) -> List[int]:
            res = [cost[a]]
            for b in g[a]:
                if b != fa:
                    res.extend(dfs(b, a))
            res.sort()
            if len(res) >= 3:
                ans[a] = max(res[-3] * res[-2] * res[-1], res[0] * res[1] * res[-1], 0)
            if len(res) > 5:
                res = res[:2] + res[-3:]
            return res

        n = len(cost)
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = [1] * n
        dfs(0, -1)
        return ans

Java

class Solution {
    private int[] cost;
    private List<Integer>[] g;
    private long[] ans;

    public long[] placedCoins(int[][] edges, int[] cost) {
        int n = cost.length;
        this.cost = cost;
        ans = new long[n];
        g = new List[n];
        Arrays.fill(ans, 1);
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int[] e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1);
        return ans;
    }

    private List<Integer> dfs(int a, int fa) {
        List<Integer> res = new ArrayList<>();
        res.add(cost[a]);
        for (int b : g[a]) {
            if (b != fa) {
                res.addAll(dfs(b, a));
            }
        }
        Collections.sort(res);
        int m = res.size();
        if (m >= 3) {
            long x = (long) res.get(m - 1) * res.get(m - 2) * res.get(m - 3);
            long y = (long) res.get(0) * res.get(1) * res.get(m - 1);
            ans[a] = Math.max(0, Math.max(x, y));
        }
        if (m >= 5) {
            res = List.of(res.get(0), res.get(1), res.get(m - 3), res.get(m - 2), res.get(m - 1));
        }
        return res;
    }
}

C++

class Solution {
public:
    vector<long long> placedCoins(vector<vector<int>>& edges, vector<int>& cost) {
        int n = cost.size();
        vector<long long> ans(n, 1);
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        function<vector<int>(int, int)> dfs = [&](int a, int fa) -> vector<int> {
            vector<int> res = {cost[a]};
            for (int b : g[a]) {
                if (b != fa) {
                    auto t = dfs(b, a);
                    res.insert(res.end(), t.begin(), t.end());
                }
            }
            sort(res.begin(), res.end());
            int m = res.size();
            if (m >= 3) {
                long long x = 1LL * res[m - 1] * res[m - 2] * res[m - 3];
                long long y = 1LL * res[0] * res[1] * res[m - 1];
                ans[a] = max({0LL, x, y});
            }
            if (m >= 5) {
                res = {res[0], res[1], res[m - 1], res[m - 2], res[m - 3]};
            }
            return res;
        };
        dfs(0, -1);
        return ans;
    }
};

Go

func placedCoins(edges [][]int, cost []int) []int64 {
	n := len(cost)
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	ans := make([]int64, n)
	for i := range ans {
		ans[i] = int64(1)
	}
	var dfs func(a, fa int) []int
	dfs = func(a, fa int) []int {
		res := []int{cost[a]}
		for _, b := range g[a] {
			if b != fa {
				res = append(res, dfs(b, a)...)
			}
		}
		sort.Ints(res)
		m := len(res)
		if m >= 3 {
			x := res[m-1] * res[m-2] * res[m-3]
			y := res[0] * res[1] * res[m-1]
			ans[a] = max(0, int64(x), int64(y))
		}
		if m >= 5 {
			res = append(res[:2], res[m-3:]...)
		}
		return res
	}
	dfs(0, -1)
	return ans
}

TypeScript

function placedCoins(edges: number[][], cost: number[]): number[] {
    const n = cost.length;
    const ans: number[] = Array(n).fill(1);
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const dfs = (a: number, fa: number): number[] => {
        const res: number[] = [cost[a]];
        for (const b of g[a]) {
            if (b !== fa) {
                res.push(...dfs(b, a));
            }
        }
        res.sort((a, b) => a - b);
        const m = res.length;
        if (m >= 3) {
            const x = res[m - 1] * res[m - 2] * res[m - 3];
            const y = res[0] * res[1] * res[m - 1];
            ans[a] = Math.max(0, x, y);
        }
        if (m > 5) {
            res.splice(2, m - 5);
        }
        return res;
    };
    dfs(0, -1);
    return ans;
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README_EN.md

README_EN.md

2973. Find Number of Coins to Place in Tree Nodes

Description

Solutions

Solution 1: DFS + Sorting

Python3

Java

C++

Go

TypeScript

Files

README_EN.md

Latest commit

History

README_EN.md

File metadata and controls

2973. Find Number of Coins to Place in Tree Nodes

Description

Solutions

Solution 1: DFS + Sorting

Python3

Java

C++

Go

TypeScript