README_EN.md

comments	difficulty	edit_url	tags
true	Easy	https://github.com/doocs/leetcode/edit/main/solution/3400-3499/3402.Minimum%20Operations%20to%20Make%20Columns%20Strictly%20Increasing/README_EN.md	Greedy Array Matrix

3402. Minimum Operations to Make Columns Strictly Increasing

中文文档

Description

You are given a m x n matrix grid consisting of non-negative integers.

In one operation, you can increment the value of any grid[i][j] by 1.

Return the minimum number of operations needed to make all columns of grid strictly increasing.

 

Example 1:

Input: grid = [[3,2],[1,3],[3,4],[0,1]]

Output: 15

Explanation:

• To make the 0th column strictly increasing, we can apply 3 operations on grid[1][0], 2 operations on grid[2][0], and 6 operations on grid[3][0].
• To make the 1st column strictly increasing, we can apply 4 operations on grid[3][1].

Example 2:

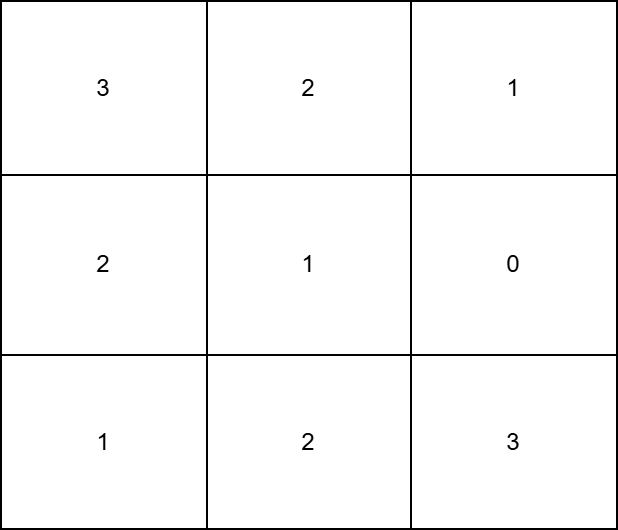
Input: grid = [[3,2,1],[2,1,0],[1,2,3]]

Output: 12

Explanation:

• To make the 0th column strictly increasing, we can apply 2 operations on grid[1][0], and 4 operations on grid[2][0].
• To make the 1st column strictly increasing, we can apply 2 operations on grid[1][1], and 2 operations on grid[2][1].
• To make the 2nd column strictly increasing, we can apply 2 operations on grid[1][2].

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• 0 <= grid[i][j] < 2500

 

Solutions

Solution 1: Column-wise Calculation

We can traverse the matrix column by column. For each column, we calculate the minimum number of operations required to make it strictly increasing. Specifically, for each column, we maintain a variable $\textit{pre}$ to represent the value of the previous element in the current column. Then, we traverse the current column from top to bottom. For the current element $\textit{cur}$, if $\textit{pre} < \textit{cur}$, it means the current element is already greater than the previous element, so we only need to update $\textit{pre} = \textit{cur}$. Otherwise, we need to increase the current element to $\textit{pre} + 1$ and add the number of increases to the answer.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns of the matrix $\textit{grid}$, respectively. The space complexity is $O(1)$.

Python3

class Solution:
    def minimumOperations(self, grid: List[List[int]]) -> int:
        ans = 0
        for col in zip(*grid):
            pre = -1
            for cur in col:
                if pre < cur:
                    pre = cur
                else:
                    pre += 1
                    ans += pre - cur
        return ans

Java

class Solution {
    public int minimumOperations(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            int pre = -1;
            for (int i = 0; i < m; ++i) {
                int cur = grid[i][j];
                if (pre < cur) {
                    pre = cur;
                } else {
                    ++pre;
                    ans += pre - cur;
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minimumOperations(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            int pre = -1;
            for (int i = 0; i < m; ++i) {
                int cur = grid[i][j];
                if (pre < cur) {
                    pre = cur;
                } else {
                    ++pre;
                    ans += pre - cur;
                }
            }
        }
        return ans;
    }
};

Go

func minimumOperations(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	for j := 0; j < n; j++ {
		pre := -1
		for i := 0; i < m; i++ {
			cur := grid[i][j]
			if pre < cur {
				pre = cur
			} else {
				pre++
				ans += pre - cur
			}
		}
	}
	return
}

TypeScript

function minimumOperations(grid: number[][]): number {
    const [m, n] = [grid.length, grid[0].length];
    let ans: number = 0;
    for (let j = 0; j < n; ++j) {
        let pre: number = -1;
        for (let i = 0; i < m; ++i) {
            const cur = grid[i][j];
            if (pre < cur) {
                pre = cur;
            } else {
                ++pre;
                ans += pre - cur;
            }
        }
    }
    return ans;
}