I was listening to this haystack, but I didn't notice anything. What did I miss?
This challenge was pretty fun -- and very very frustrating when I had no idea what I was doing or where to go next. (I'm reminded of that time when I accidentally mirror-inverted then rotated the QR code I was trying to de-corrupt and decode, and so of course didn't make any progress at all...)
From the title 'Serial', it was pretty likely that this would be a stream of serial data, so all I had to do was decode that, right? Super easy, right?
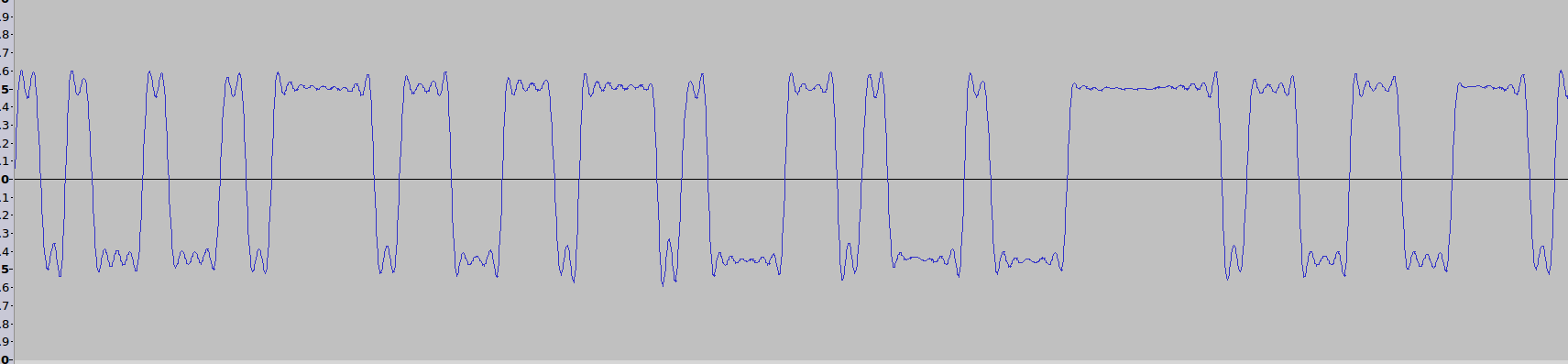
I opened the audio file in audacity. This is pretty much always worth doing for any sort of forensics-y audio file: often it looks interesting either in the waveform view (if you zoom in enough), or in the spectrogram view (check out both linear and log scales).
Figure 1: screenshot of .wav opened in audacity. there are very obvious high/low "values".
Okay, cool, let's try to convert the low/high from the audio file to a stream of 0s and 1s.
I started out in hexinator (fantastic hex editor, 10/10 highly
recommended for CTF stuff --
https://hexinator.com/) to check out the
headers/metadata (and get the offset for where the data started), and to
see if anything stood out in the raw bytes. (You can also get the
metadata using ffprobe, and stare at the hexdump using xxd,
which could be better if you're in a hurry.)
The wav file stored sounds as 16 bit values, which means they will range between roughly -32760 and 32760.
I opened the wav file as raw bytes in python, started from the first byte after the header ended, and printed them out to see if I could see any obvious patterns -- ideally, it would be super trivial to get the low/high out of the audio file.
a = open("easyctf_serial.wav", "rb").read()
b = a[44:] # the header is 44 bytes long, skip to the data
# take every two bytes, and interpret them as a short integer, storing
# it in an array
raw_bytes = [struct.unpack('h', ''.join(b[i : i+2]))[0] for i in
xrange(0, len(b), 2)]And, indeed there was: the numbers all fluctuated around roughly -1000 to -2000 for a while, then suddenly jumped slightly positive (300, 1000, 1400, 1650, 1400, 870) then suddenly very negative (down to about -20000). They stuck around being very negative for a bit, then jumped up to slightly positive, then back down to very negative, forming the square-ish wave-y shapes seen in the picture above.
Unfortunately, there was no nice obvious cutoff for what defined low vs high: you can see in the screenshot below that the 'low' starts out pretty low, but the 'high' starts out barely above the centre line (those slightly-positive numbers: maxing out at 1650 (out of a possible max of 32760) initially.
Figure 2: you can see that the audio file starts out with low/high being shifted lower, then levels out to low/high being roughly symmetrical
I worked out the relative low/high based on where a given value fell between the biggest and smallest values we'd seen thus far; through trial and error, taking anything that was in the top 65% as high and the bottom 45% as low worked out pretty well.
for cur in raw_bytes:
# update bounds
if cur < c_min:
c_min = cur
if cur > c_max:
c_max = cur
pos = (cur-c_min)/float(c_max+1 - c_min) # avoid div by 0
# where are we in relation to the biggest/smallest we've seen so far?
print "%6d: %f | %6d %6d" % (cur, pos, c_min, c_max)
if pos > 0.65:
# we're in an upswing
print ">>> 1"
elif pos < 0.35:
# downswing
print ">>> 0"Some sample output:
current_value relative_pos min max
1492: 0.974809 | -20836 2068
>>> 1
807: 0.944903 | -20836 2068
>>> 1
-40: 0.907924 | -20836 2068
>>> 1
-941: 0.868588 | -20836 2068
>>> 1
-1804: 0.830910 | -20836 2068
>>> 1
-2552: 0.798254 | -20836 2068
>>> 1
-3089: 0.774809 | -20836 2068
>>> 1
-3393: 0.761537 | -20836 2068
>>> 1
-3405: 0.761013 | -20836 2068
>>> 1
-3157: 0.771840 | -20836 2068
>>> 1
-2658: 0.793626 | -20836 2068
>>> 1
-1976: 0.823401 | -20836 2068
>>> 1
-1168: 0.858677 | -20836 2068
>>> 1
-338: 0.894914 | -20836 2068
>>> 1
433: 0.928575 | -20836 2068
>>> 1
1050: 0.955512 | -20836 2068
>>> 1
1428: 0.972015 | -20836 2068
>>> 1
1511: 0.975639 | -20836 2068
>>> 1
1249: 0.964200 | -20836 2068
>>> 1
618: 0.936651 | -20836 2068
>>> 1
-364: 0.893779 | -20836 2068
>>> 1
-1682: 0.836237 | -20836 2068
>>> 1
-3271: 0.766863 | -20836 2068
>>> 1
-5073: 0.688190 | -20836 2068
>>> 1
-6989: 0.604540 | -20836 2068
-8959: 0.518533 | -20836 2068
-10871: 0.435058 | -20836 2068
-12668: 0.356603 | -20836 2068
-14275: 0.286444 | -20836 2068
>>> 0
-15647: 0.226544 | -20836 2068
>>> 0
-16748: 0.178476 | -20836 2068
>>> 0
-17581: 0.142109 | -20836 2068
>>> 0
-18130: 0.118140 | -20836 2068
>>> 0
-18449: 0.104213 | -20836 2068
>>> 0
-18540: 0.100240 | -20836 2068
>>> 0
-18478: 0.102947 | -20836 2068
>>> 0
-18291: 0.111111 | -20836 2068
>>> 0
-18040: 0.122069 | -20836 2068
>>> 0
From here I disregarded the actual raw values, and just looked at the 0s and 1s I'd bucketed them into. From looking at the wav in audacity I could see that each bit was a certain duration of low/high, and multiple 0s or 1s in a row were a longer duration of low/high. So, I counted the number of consecutive 0s or 1s:
# this comes in handy later
def print_counter(counter):
print counter
for cur in raw_bytes:
# update bounds
if cur < c_min:
c_min = cur
if cur > c_max:
c_max = cur
if started: # disregard the non-useful section at the start
counter += 1
pos = (cur-c_min)/float(c_max+1 - c_min) # avoid div by 0
if pos > 0.65:
# we're in an upswing
if cur_val == 0:
# swapping
print_counter(counter)
counter = 0
cur_val = 1
elif pos < 0.35:
# downswing
if cur_val == 1:
# swapping
print_counter(counter)
counter = 0
cur_val = 0
else:
if cur < -5000:
# we hit the first drop
started = True
counter = 0Sample output:
78
44
35
286
115
44
34
46
118
83
76
124
36
84
35
86
35
86
45
36
45
35
84
75
85
78
44
35
44
115
125
118
202
36
84
36
45
There was a pretty clear pattern here: the length of a run of consecutive bits was roughly a multiple of 40.
So, I converted these to how many multiples of 40 they were, and appended that many zeroes or ones to my stream of bits.
def print_counter(counter, numbers, cur):
# print counter
num_multiples = (counter+20)/40
for p in xrange(num_multiples):
numbers.append(str(1-cur)) # flopped bitsNow that we have the raw stream of bits, it's time to try decoding it.
At first glance there wasn't anything obvious; I did some reading on how
serial communication and common serial protocols work, and discovered
that a serial stream probably has start/stop bits (and possibly also
parity bits).
So, I set out looking for patterns: did the same value occur every n
bits?
cur_val = -1
for interval in xrange(1,20):
for start in xrange(80):
failed = False
for upto in xrange(start, len(numbers), interval):
print upto
if cur_val == -1:
cur_val = int(numbers[upto])
continue
if int(numbers[upto]) != cur_val:
print "%d doesn't match %d (counter %d, interval %d, start %d)" %
(int(numbers[upto]), cur_val, upto, interval, start)
failed = True
break
if failed == False:
print ">>>>>>>>>>>>>>> success!!! cur_val %d, count %d, int %d, start %d)" %
(cur_val, upto, interval, start)
cur_val = -1>>>>>>>>>>>>>>> success!!!
val 0, count 12364, int 11, start 0)
>>>>>>>>>>>>>>> success!!!
val 0, count 12365, int 11, start 1)
>>>>>>>>>>>>>>> success!!!
val 1, count 12366, int 11, start 2)
>>>>>>>>>>>>>>> success!!!
val 0, count 12364, int 11, start 11)
>>>>>>>>>>>>>>> success!!!
val 0, count 12365, int 11, start 12)
>>>>>>>>>>>>>>> success!!!
val 1, count 12366, int 11, start 13)
>>>>>>>>>>>>>>> success!!!
val 0, count 12364, int 11, start 22)
>>>>>>>>>>>>>>> success!!!
val 0, count 12365, int 11, start 23)
>>>>>>>>>>>>>>> success!!!
val 1, count 12366, int 11, start 24)
Cool, we can see that every 11 bits, we have the pattern 001. eg:
001XXXXXXXX001XXXXXXXX001. Conveniently, 11 bits - 3 recurring bits = 8
bits = 1 byte of data = (y)
Time to write the raw bytes out to a file, and see if it looks at all meaningful.
byte_length = 11
ignore = 3
with open(files[0], 'wb') as filename:
filename.write(''.join(chr(int(''.join(numbers[
byte_length*k:byte_length*k+byte_length][ignore:][::-1])
, 2)) for k in xrange(len(numbers)/byte_length)))That's a particularly messy blob of python, so, breaking it down:
-
take our list of binary bits, in blocks of 11 bits at a time
-
ignore the first three of those bits, and join the remaining 8 together
-
reverse those 8 bits, because the bits are received in the opposite order
-
convert to an integer number, and then convert that to a character
-
do that for all of the bits, then glue all of those characters together, and write them to a file
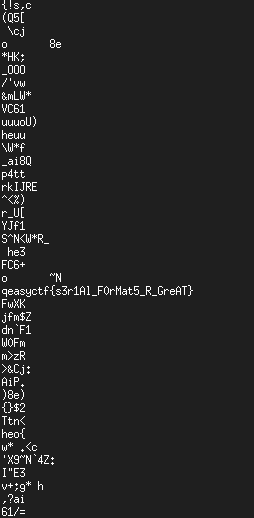
Time to see if there's anything useful in the file. run it through
strings, and less the output: there's a whole bunch of random
data, then eventually.....
Figure 3: found the flag!
This is just the story of the things I did that actually worked. I spent a lot of time trying a lot of things that didn't work in the process:
-
not finding the start/stop bits and staring into the void having no idea how to progress
-
not reversing the endianness of the bits
-
inverting the bits so low is 1 and high is 0
-
trying really really hard to find meaning in anything there
-
failing very hard at decoding the binary by hand (everything looks like a binary-ascii 'e' when you're desperate)
-
trying to decode it using some sort of automated tool (and failing -- but hey it's 9600 baud, 1 start bit, no parity bits, 2 stop bits, so at least I learned how to work that out and what that means)
In the end, I solved it by taking all combinations of low=0 high=1 vs
low=1 high=0 and the order of the bits is least significant to most significant vs most significant to least significant, running all of
those through strings, piping all of that into less, and dramatically
scrolling through it looking for anything of significance.
(I didn't just strings | grep 'easyctf', because that had failed before
and I wasn't expecting to find a flag, just hoping to find out some more
information on anything at all that might help me progress.)
And now for the encore: there was a hint given for this challenge:
1671272170308973364559718095536342710762555701423308167532544584.
I spent a lot of time staring at it in frustration trying to work out what it could possibly mean. They weren't ascii characters. There was no obvious way to break it up into smaller numbers. Hm, but the binary version looked interesting...
1000001000000001001000001001000000001000001000001001001000000001000000001001000001000000001000001001000000000000001000001001000001001000000000000001000001001001000000000001000001001001000000000001000001001001000
Look at how wide the 'gaps' are between each of the 1s. Looking at the pattern....
5 8 2 5 2 8 5 5 2 2 8 8 2 5 8 5 2
1000001000000001001000001001000000001000001000001001001000000001000000001001000001000000001000001001
14 5 2 5 2 14 5 2 2 11 5 2 2 11 5
(1)000000000000001000001001000001001000000000000001000001001001000000000001000001001001000000000001000001
2 2 3
(1)001001000
There seemed to be some type of pattern going on here, and a friend commented that they stood out as numbers that occured in the value of 1/7 (== 0.142857142...). This led to messing around with other bases, and discovering that if you converted it to octal.....
10100110110010101110010011010010110000101101100001011100010111000101110
Would you look at that -- it's a binary string. And, would you look at that... do I sense some ASCII?
Converting it to hex makes it a lot clearer: 0x53657269616c2e2e2e.
(sidenote: if you can't convert hexadecimal values to their ASCII
equivalent in your head, I highly recommend learning: in the very least,
if you can look at a hex (or binary) string and go "huh those are
printable ASCII values" it can speed things up a lot in CTFs. (also in
"cyber-crime" themed escape rooms.))
>>> for thing in [0x53, 0x65, 0x72, 0x69, 0x61, 0x6c, 0x2e, 0x2e, 0x2e]:
... print chr(thing),
S e r i a l . . ....... yep, I think they're trolling us a bit with that hint.
- (none)