README_EN.md

429. N-ary Tree Level Order Traversal

中文文档

Description

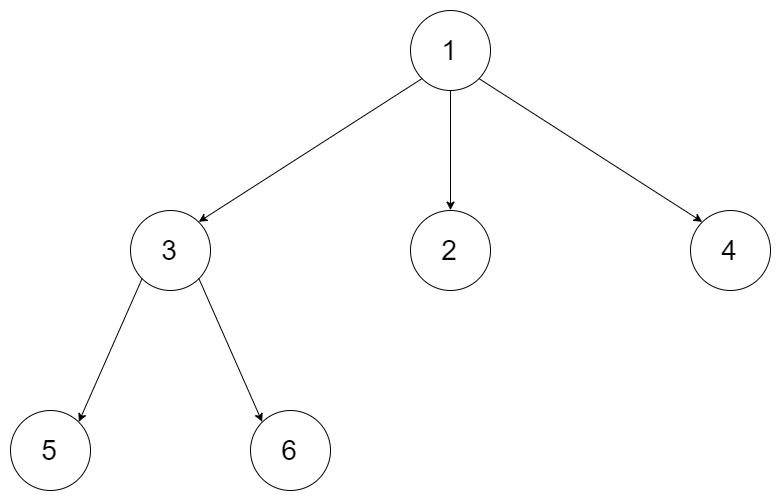
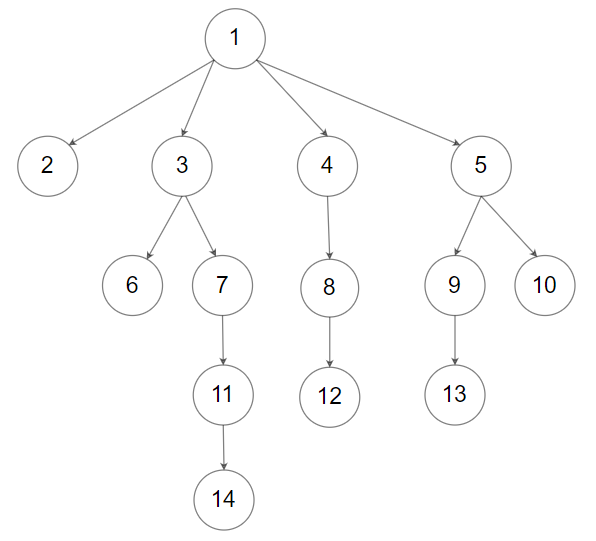
Given an n-ary tree, return the level order traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

 

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [[1],[3,2,4],[5,6]]

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

 

Constraints:

• The height of the n-ary tree is less than or equal to 1000
• The total number of nodes is between [0, 104]

Solutions

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution:
    def levelOrder(self, root: 'Node') -> List[List[int]]:
        if root is None:
            return []
        q = deque([root])
        res = []
        while q:
            n = len(q)
            t = []
            for _ in range(n):
                node = q.popleft()
                t.append(node.val)
                if node.children:
                    q.extend(node.children)
            res.append(t)
        return res

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        if (root == null) {
            return Collections.emptyList();
        }
        Deque<Node> q = new ArrayDeque<>();
        List<List<Integer>> res = new ArrayList<>();
        q.offer(root);
        while (!q.isEmpty()) {
            List<Integer> t = new ArrayList<>();
            for (int i = 0, n = q.size(); i < n; ++i) {
                Node node = q.poll();
                t.add(node.val);
                if (node.children != null) {
                    q.addAll(node.children);
                }
            }
            res.add(t);
        }
        return res;
    }
}

...