你的面前有一堵矩形的、由多行砖块组成的砖墙。 这些砖块高度相同但是宽度不同。你现在要画一条自顶向下的、穿过最少砖块的垂线。
砖墙由行的列表表示。 每一行都是一个代表从左至右每块砖的宽度的整数列表。
如果你画的线只是从砖块的边缘经过,就不算穿过这块砖。你需要找出怎样画才能使这条线穿过的砖块数量最少,并且返回穿过的砖块数量。
你不能沿着墙的两个垂直边缘之一画线,这样显然是没有穿过一块砖的。
示例:
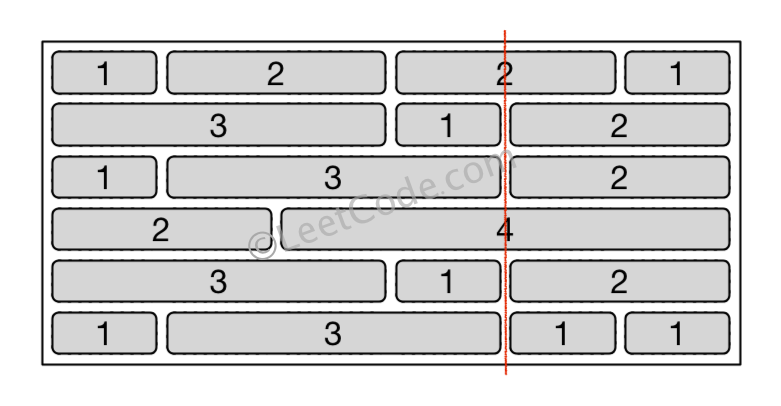
输入: [[1,2,2,1],
[3,1,2],
[1,3,2],
[2,4],
[3,1,2],
[1,3,1,1]]
输出: 2
解释:
提示:
- 每一行砖块的宽度之和应该相等,并且不能超过 INT_MAX。
- 每一行砖块的数量在 [1,10,000] 范围内, 墙的高度在 [1,10,000] 范围内, 总的砖块数量不超过 20,000。
题目可以理解为,让垂线尽可能多地穿过砖块边缘,用哈希表处理不同位置的砖块边缘出现的频次(不包括两个垂直边缘),最终的答案就是总行数减去最大频数。
class Solution:
def leastBricks(self, wall: List[List[int]]) -> int:
cnt = defaultdict(int)
for row in wall:
width = 0
for brick in row[:-1]:
width += brick
cnt[width] += 1
if not cnt:
return len(wall)
return len(wall) - cnt[max(cnt, key=cnt.get)]class Solution {
public int leastBricks(List<List<Integer>> wall) {
Map<Integer, Integer> cnt = new HashMap<>();
for (List<Integer> row : wall) {
int width = 0;
for (int i = 0, n = row.size() - 1; i < n; i++) {
width += row.get(i);
cnt.merge(width, 1, Integer::sum);
}
}
int max = cnt.values().stream().max(Comparator.naturalOrder()).orElse(0);
return wall.size() - max;
}
}func leastBricks(wall [][]int) int {
cnt := make(map[int]int)
for _, row := range wall {
width := 0
for _, brick := range row[:len(row)-1] {
width += brick
cnt[width]++
}
}
max := 0
for _, v := range cnt {
if v > max {
max = v
}
}
return len(wall) - max
}/**
* @param {number[][]} wall
* @return {number}
*/
var leastBricks = function (wall) {
const cnt = new Map();
for (const row of wall) {
let width = 0;
for (let i = 0, n = row.length - 1; i < n; ++i) {
width += row[i];
cnt.set(width, (cnt.get(width) || 0) + 1);
}
}
let max = 0;
for (const v of cnt.values()) {
max = Math.max(max, v);
}
return wall.length - max;
};
