README_EN.md

1135. Connecting Cities With Minimum Cost

中文文档

Description

There are N cities numbered from 1 to N.

You are given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together.  (A connection is bidirectional: connecting city1 and city2 is the same as connecting city2 and city1.)

Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together.  The cost is the sum of the connection costs used. If the task is impossible, return -1.

 

Example 1:

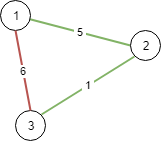
Input: N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]
Output: 6
Explanation: 
Choosing any 2 edges will connect all cities so we choose the minimum 2.

Example 2:

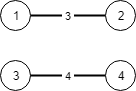
Input: N = 4, connections = [[1,2,3],[3,4,4]]
Output: -1
Explanation: 
There is no way to connect all cities even if all edges are used.

 

Note:

1. 1 <= N <= 10000
2. 1 <= connections.length <= 10000
3. 1 <= connections[i][0], connections[i][1] <= N
4. 0 <= connections[i][2] <= 10^5
5. connections[i][0] != connections[i][1]

Solutions

Python3

class Solution:
    def minimumCost(self, n: int, connections: List[List[int]]) -> int:
        p = list(range(n))
        connections.sort(key=lambda x: x[2])
        res = 0

        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        def union(a, b):
            pa, pb = find(a - 1), find(b - 1)
            if pa == pb:
                return False
            p[pa] = pb
            return True

        for c1, c2, cost in connections:
            if union(c1, c2):
                n -= 1
                res += cost
                if n == 1:
                    return res
        return -1

Java

class Solution {
    private int[] p;

    public int minimumCost(int n, int[][] connections) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        Arrays.sort(connections, (a, b) -> a[2] - b[2]);
        int res = 0;
        for (int[] e : connections) {
            if (union(e[0], e[1])) {
                res += e[2];
                --n;
                if (n == 1) {
                    return res;
                }
            }
        }
        return -1;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    private boolean union(int a, int b) {
        int pa = find(a - 1), pb = find(b - 1);
        if (pa == pb) {
            return false;
        }
        p[pa] = pb;
        return true;
    }
}

C++

class Solution {
public:
    vector<int> p;

    int minimumCost(int n, vector<vector<int>> &connections) {
        p.resize(n);
        for (int i = 0; i < n; ++i) p[i] = i;
        auto cmp = [](auto &a, auto &b)
        {
            return a[2] < b[2];
        };
        sort(connections.begin(), connections.end(), cmp);
        int res = 0;
        for (auto e : connections)
        {
            if (unite(e[0], e[1]))
            {
                res += e[2];
                --n;
                if (n == 1) return res;
            }
        }
        return -1;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    bool unite(int a, int b) {
        int pa = find(a - 1), pb = find(b - 1);
        if (pa == pb) return false;
        p[pa] = pb;
        return true;
    }
};

Go

var p []int

func minimumCost(n int, connections [][]int) int {
	p = make([]int, n)
	for i := 0; i < len(p); i++ {
		p[i] = i
	}
	sort.Slice(connections, func(i, j int) bool {
		return connections[i][2] < connections[j][2]
	})
	res := 0
	for _, e := range connections {
		if union(e[0], e[1]) {
			res += e[2]
			n--
			if n == 1 {
				return res
			}
		}
	}
	return -1
}

func find(x int) int {
	if p[x] != x {
		p[x] = find(p[x])
	}
	return p[x]
}

func union(a, b int) bool {
	pa, pb := find(a-1), find(b-1)
	if pa == pb {
		return false
	}
	p[pa] = pb
	return true
}

...