在一个 8x8 的棋盘上,放置着若干「黑皇后」和一个「白国王」。
「黑皇后」在棋盘上的位置分布用整数坐标数组 queens 表示,「白国王」的坐标用数组 king 表示。
「黑皇后」的行棋规定是:横、直、斜都可以走,步数不受限制,但是,不能越子行棋。
请你返回可以直接攻击到「白国王」的所有「黑皇后」的坐标(任意顺序)。
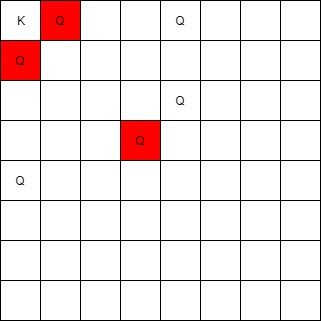
示例 1:
输入:queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0] 输出:[[0,1],[1,0],[3,3]] 解释: [0,1] 的皇后可以攻击到国王,因为他们在同一行上。 [1,0] 的皇后可以攻击到国王,因为他们在同一列上。 [3,3] 的皇后可以攻击到国王,因为他们在同一条对角线上。 [0,4] 的皇后无法攻击到国王,因为她被位于 [0,1] 的皇后挡住了。 [4,0] 的皇后无法攻击到国王,因为她被位于 [1,0] 的皇后挡住了。 [2,4] 的皇后无法攻击到国王,因为她和国王不在同一行/列/对角线上。
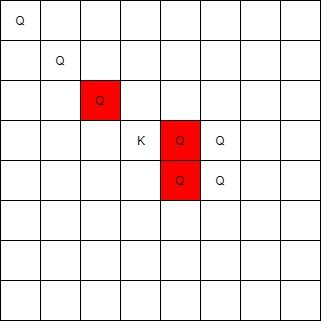
示例 2:
输入:queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3] 输出:[[2,2],[3,4],[4,4]]
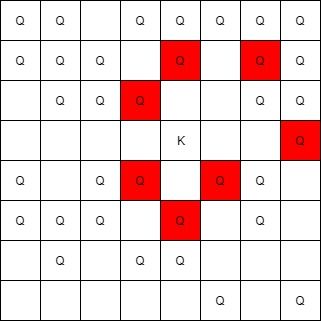
示例 3:
输入:queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4] 输出:[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]
提示:
1 <= queens.length <= 63queens[i].length == 20 <= queens[i][j] < 8king.length == 20 <= king[0], king[1] < 8- 一个棋盘格上最多只能放置一枚棋子。
先将所有 queens 存放到一个哈希表中。
然后从 king 位置,循环遍历 “上、下、左、右、对角线”等 8 个方向。对于每个方向,碰到第一个 queen 时,将该 queen 加到结果列表中,然后结束此方向的遍历。
最后返回结果列表 ans 即可。
class Solution:
def queensAttacktheKing(self, queens: List[List[int]], king: List[int]) -> List[List[int]]:
n = 8
s = set((i, j) for i, j in queens)
ans = []
for a, b in [[-1, 0], [1, 0], [0, -1], [0, 1], [1, 1], [1, -1], [-1, 1], [-1, -1]]:
x, y = king
while 0 <= x + a < n and 0 <= y + b < n:
x, y = x + a, y + b
if (x, y) in s:
ans.append([x, y])
break
return ansclass Solution {
private static final int N = 8;
private int[][] dirs = new int[][]{{0, -1}, {0, 1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
Set<Integer> s = get(queens);
List<List<Integer>> ans = new ArrayList<>();
for (int[] dir : dirs) {
int x = king[0], y = king[1];
int a = dir[0], b = dir[1];
while (x + a >= 0 && x + a < N && y + b >= 0 && y + b < N) {
x += a;
y += b;
if (s.contains(x * N + y)) {
ans.add(Arrays.asList(x, y));
break;
}
}
}
return ans;
}
private Set<Integer> get(int[][] queens) {
Set<Integer> ans = new HashSet<>();
for (int[] queen : queens) {
ans.add(queen[0] * N + queen[1]);
}
return ans;
}
}class Solution {
public:
vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {
unordered_set<int> s;
int n = 8;
for (auto& queen : queens) s.insert(queen[0] * n + queen[1]);
vector<vector<int>> dirs = {{0, 1}, {0, - 1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
vector<vector<int>> ans;
for (auto& dir : dirs)
{
int x = king[0], y = king[1];
int a = dir[0], b = dir[1];
while (x + a >= 0 && x + a < n && y + b >= 0 && y + b < n)
{
x += a;
y += b;
if (s.count(x * n + y))
{
ans.push_back({x, y});
break;
}
}
}
return ans;
}
};func queensAttacktheKing(queens [][]int, king []int) [][]int {
s := make(map[int]bool)
n := 8
for _, queen := range queens {
s[queen[0]*n+queen[1]] = true
}
dirs := [8][2]int{{0, -1}, {0, 1}, {1, 0}, {-1, 0}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}}
var ans [][]int
for _, dir := range dirs {
x, y := king[0], king[1]
a, b := dir[0], dir[1]
for x+a >= 0 && x+a < n && y+b >= 0 && y+b < n {
x, y = x+a, y+b
if s[x*n+y] {
ans = append(ans, []int{x, y})
break
}
}
}
return ans
}