给定一棵 N 叉树的根节点 root ,计算这棵树的直径长度。
N 叉树的直径指的是树中任意两个节点间路径中 最长 路径的长度。这条路径可能经过根节点,也可能不经过根节点。
(N 叉树的输入序列以层序遍历的形式给出,每组子节点用 null 分隔)
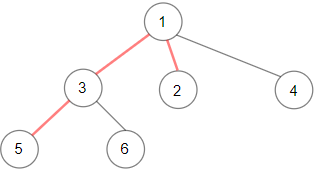
示例 1:
输入:root = [1,null,3,2,4,null,5,6] 输出:3 解释:直径如图中红线所示。
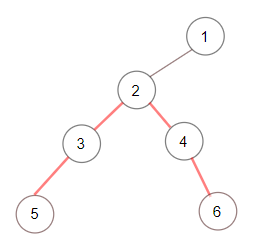
示例 2:
输入:root = [1,null,2,null,3,4,null,5,null,6] 输出:4
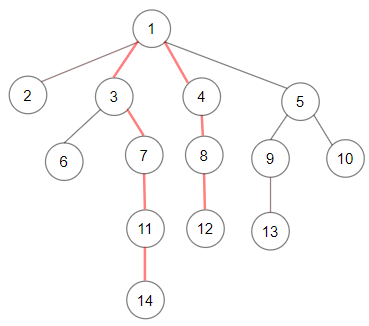
示例 3:
输入: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出: 7
提示:
- N 叉树的深度小于或等于
1000。 - 节点的总个数在
[0, 10^4]间。
方法一:后序遍历求每个结点的深度,此过程中获取每个结点子树的最长两个伸展(深度),迭代获取最长路径。
类似题目:543. 二叉树的直径
方法二:两次 DFS。
首先对任意一个结点做 DFS 求出最远的结点,然后以这个结点为根结点再做 DFS 到达另一个最远结点。第一次 DFS 到达的结点可以证明一定是这个图的直径的一端,第二次 DFS 就会达到另一端。下面来证明这个定理。
定理:在一个连通无向无环图中,以任意结点出发所能到达的最远结点,一定是该图直径的端点之一。
证明:假设这条直径是 δ(s, t)。分两种情况:
-
当出发结点 y 在 δ(s, t) 时,假设到达的最远结点 z 不是 s, t 中的任一个。这时将 δ(y, z) 与不与之重合的 δ(y, s) 拼接(也可以假设不与之重合的是直径的另一个方向),可以得到一条更长的直径,与前提矛盾。
-
当出发结点 y 不在 δ(s, t) 上时,分两种情况:
- 当 y 到达的最远结点 z 横穿 δ(s, t) 时,记与之相交的结点为 x。此时有 δ(y, z) = δ(y, x) + δ(x, z)。而此时 δ(y, z) > δ(y, t),故可得 δ(x, z) > δ(x, t)。由 1 的结论可知该假设不成立。
- 当 y 到达的最远结点 z 与 δ(s, t) 不相交时,定义从 y 开始到 t 结束的简单路径上,第一个同时也存在于简单路径 δ(s, t) 上的结点为 x,最后一个存在于简单路径 δ(y, z) 上的结点为 x’。如下图。那么根据假设,有 δ(y, z) ≥ δ(y, t) => δ(x', z) ≥ δ(x', x) + δ(x, t)。既然这样,那么 δ(x, z) ≥ δ(x, t),和 δ(s, t) 对应着直径这一前提不符,故 y 的最远结点 z 不可能在 s 到 t 这个直径对应的路外面。
因此定理成立。
类似题目:1245. 树的直径
"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children if children is not None else []
"""
class Solution:
def diameter(self, root: 'Node') -> int:
"""
:type root: 'Node'
:rtype: int
"""
def dfs(root):
if root is None:
return 0
nonlocal ans
m1 = m2 = 0
for child in root.children:
t = dfs(child)
if t > m1:
m2, m1 = m1, t
elif t > m2:
m2 = t
ans = max(ans, m1 + m2)
return 1 + m1
ans = 0
dfs(root)
return ans"""
# Definition for a Node.
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children if children is not None else []
"""
class Solution:
def diameter(self, root: 'Node') -> int:
"""
:type root: 'Node'
:rtype: int
"""
def build(root):
nonlocal d
if root is None:
return
for child in root.children:
d[root].add(child)
d[child].add(root)
build(child)
def dfs(u, t):
nonlocal ans, vis, d, next
if u in vis:
return
vis.add(u)
for v in d[u]:
dfs(v, t + 1)
if ans < t:
ans = t
next = u
d = defaultdict(set)
vis = set()
build(root)
ans = 0
next = None
dfs(root, 0)
vis.clear()
dfs(next, 0)
return ans/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {
children = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
children = new ArrayList<Node>();
}
public Node(int _val,ArrayList<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
private int ans;
public int diameter(Node root) {
ans = 0;
dfs(root);
return ans;
}
private int dfs(Node root) {
if (root == null) {
return 0;
}
int m1 = 0, m2 = 0;
for (Node child : root.children) {
int t = dfs(child);
if (t > m1) {
m2 = m1;
m1 = t;
} else if (t > m2) {
m2 = t;
}
}
ans = Math.max(ans, m1 + m2);
return 1 + m1;
}
}/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {
children = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
children = new ArrayList<Node>();
}
public Node(int _val,ArrayList<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
private Map<Node, Set<Node>> g;
private Set<Node> vis;
private Node next;
private int ans;
public int diameter(Node root) {
g = new HashMap<>();
build(root);
vis = new HashSet<>();
next = root;
ans = 0;
dfs(next, 0);
vis.clear();
dfs(next, 0);
return ans;
}
private void dfs(Node u, int t) {
if (vis.contains(u)) {
return;
}
vis.add(u);
if (t > ans) {
ans = t;
next = u;
}
if (g.containsKey(u)) {
for (Node v : g.get(u)) {
dfs(v, t + 1);
}
}
}
private void build(Node root) {
if (root == null) {
return;
}
for (Node child : root.children) {
g.computeIfAbsent(root, k -> new HashSet<>()).add(child);
g.computeIfAbsent(child, k -> new HashSet<>()).add(root);
build(child);
}
}
}/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
int ans;
int diameter(Node* root) {
ans = 0;
dfs(root);
return ans;
}
int dfs(Node* root) {
if (!root) return 0;
int m1 = 0, m2 = 0;
for (Node* child : root->children)
{
int t = dfs(child);
if (t > m1)
{
m2 = m1;
m1 = t;
}
else if (t > m2) m2 = t;
}
ans = max(ans, m1 + m2);
return 1 + m1;
}
};/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
unordered_map<Node*, unordered_set<Node*>> g;
unordered_set<Node*> vis;
Node* next;
int ans;
int diameter(Node* root) {
build(root);
next = root;
ans = 0;
dfs(next, 0);
vis.clear();
dfs(next, 0);
return ans;
}
void dfs(Node* u, int t) {
if (vis.count(u)) return;
vis.insert(u);
if (ans < t)
{
ans = t;
next = u;
}
if (g.count(u))
for (Node* v : g[u])
dfs(v, t + 1);
}
void build(Node* root) {
if (!root) return;
for (Node* child : root->children)
{
g[root].insert(child);
g[child].insert(root);
build(child);
}
}
};/**
* Definition for a Node.
* type Node struct {
* Val int
* Children []*Node
* }
*/
func diameter(root *Node) int {
ans := 0
var dfs func(root *Node) int
dfs = func(root *Node) int {
if root == nil {
return 0
}
m1, m2 := 0, 0
for _, child := range root.Children {
t := dfs(child)
if t > m1 {
m2, m1 = m1, t
} else if t > m2 {
m2 = t
}
}
ans = max(ans, m1+m2)
return 1 + m1
}
dfs(root)
return ans
}
func max(a, b int) int {
if a > b {
return a
}
return b
}/**
* Definition for a Node.
* type Node struct {
* Val int
* Children []*Node
* }
*/
func diameter(root *Node) int {
g := make(map[*Node][]*Node)
vis := make(map[*Node]bool)
next := root
ans := 0
var build func(root *Node)
build = func(root *Node) {
if root == nil {
return
}
for _, child := range root.Children {
g[root] = append(g[root], child)
g[child] = append(g[child], root)
build(child)
}
}
build(root)
var dfs func(u *Node, t int)
dfs = func(u *Node, t int) {
if vis[u] {
return
}
vis[u] = true
if t > ans {
ans = t
next = u
}
if vs, ok := g[u]; ok {
for _, v := range vs {
dfs(v, t+1)
}
}
}
dfs(next, 0)
vis = make(map[*Node]bool)
dfs(next, 0)
return ans
}