README_EN.md

1552. Magnetic Force Between Two Balls

中文文档

Description

In universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the ith basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.

Rick stated that magnetic force between two different balls at positions x and y is |x - y|.

Given the integer array position and the integer m. Return the required force.

 

Example 1:

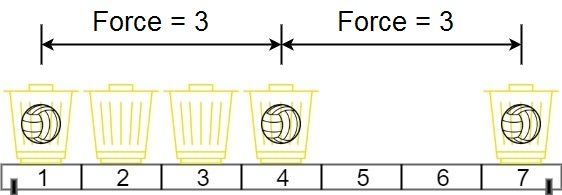
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.

Example 2:

Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.

 

Constraints:

• n == position.length
• 2 <= n <= 10^5
• 1 <= position[i] <= 10^9
• All integers in position are distinct.
• 2 <= m <= position.length

Solutions

Python3

class Solution:
    def maxDistance(self, position: List[int], m: int) -> int:
        position.sort()

        def check(f):
            pre = position[0]
            cnt = 1
            for pos in position[1:]:
                if pos - pre >= f:
                    cnt += 1
                    pre = pos
            return cnt >= m

        left, right = 1, position[-1]
        while left < right:
            mid = (left + right + 1) >> 1
            if check(mid):
                left = mid
            else:
                right = mid - 1
        return left

Java

class Solution {
    public int maxDistance(int[] position, int m) {
        Arrays.sort(position);
        int left = 1, right = position[position.length - 1];
        while (left < right) {
            int mid = (left + right + 1) >> 1;
            if (check(position, mid, m)) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return left;
    }

    private boolean check(int[] position, int f, int m) {
        int pre = position[0];
        int cnt = 1;
        for (int i = 1; i < position.length; ++i) {
            if (position[i] - pre >= f) {
                ++cnt;
                pre = position[i];
            }
        }
        return cnt >= m;
    }
}

C++

class Solution {
public:
    int maxDistance(vector<int>& position, int m) {
        sort(position.begin(), position.end());
        int left = 1, right = position[position.size() - 1];
        while (left < right) {
            int mid = (left + right + 1) >> 1;
            if (check(position, mid, m)) left = mid;
            else right = mid - 1;
        }
        return left;
    }

    bool check(vector<int>& position, int f, int m) {
        int pre = position[0];
        int cnt = 1;
        for (int i = 1; i < position.size(); ++i) {
            if (position[i] - pre >= f) {
                ++cnt;
                pre = position[i];
            }
        }
        return cnt >= m;
    }
};

Go

func maxDistance(position []int, m int) int {
	sort.Ints(position)
	left, right := 1, position[len(position)-1]
	for left < right {
		mid := (left + right + 1) >> 1
		if check(position, mid, m) {
			left = mid
		} else {
			right = mid - 1
		}
	}
	return left
}

func check(position []int, f, m int) bool {
	pre, cnt := position[0], 1
	for i := 1; i < len(position); i++ {
		if position[i]-pre >= f {
			cnt++
			pre = position[i]
		}
	}
	return cnt >= m
}

...