给定一棵二叉树的根节点 root,返回给定节点 p 和 q 的最近公共祖先(LCA)节点。如果 p 或 q 之一不存在于该二叉树中,返回 null。树中的每个节点值都是互不相同的。
根据维基百科中对最近公共祖先节点的定义:“两个节点 p 和 q 在二叉树 T 中的最近公共祖先节点是后代节点中既包括 p 又包括 q 的最深节点(我们允许一个节点为自身的一个后代节点)”。一个节点 x 的后代节点是节点 x 到某一叶节点间的路径中的节点 y。
示例 1:
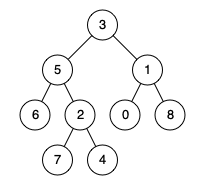
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和 1 的共同祖先节点是 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和 4 的共同祖先节点是 5。根据共同祖先节点的定义,一个节点可以是自身的后代节点。
示例 3:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 10 输出: null 解释: 节点 10 不存在于树中,所以返回 null。
提示:
- 树中节点个数的范围是
[1, 104]。 -109 <= Node.val <= 109- 所有节点的值
Node.val是互不相同的。 p != q