README_EN.md

1660. Correct a Binary Tree

中文文档

Description

You have a binary tree with a small defect. There is exactly one invalid node where its right child incorrectly points to another node at the same depth but to the invalid node's right.

Given the root of the binary tree with this defect, root, return the root of the binary tree after removing this invalid node and every node underneath it (minus the node it incorrectly points to).

Custom testing:

The test input is read as 3 lines:

• TreeNode root
• int fromNode (not available to correctBinaryTree)
• int toNode (not available to correctBinaryTree)

After the binary tree rooted at root is parsed, the TreeNode with value of fromNode will have its right child pointer pointing to the TreeNode with a value of toNode. Then, root is passed to correctBinaryTree.

 

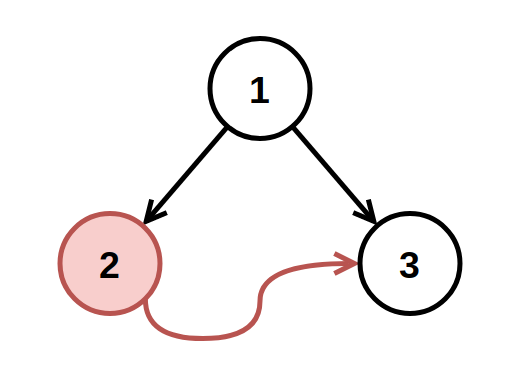
Example 1:

Input: root = [1,2,3], fromNode = 2, toNode = 3

Output: [1,null,3]

Explanation: The node with value 2 is invalid, so remove it.

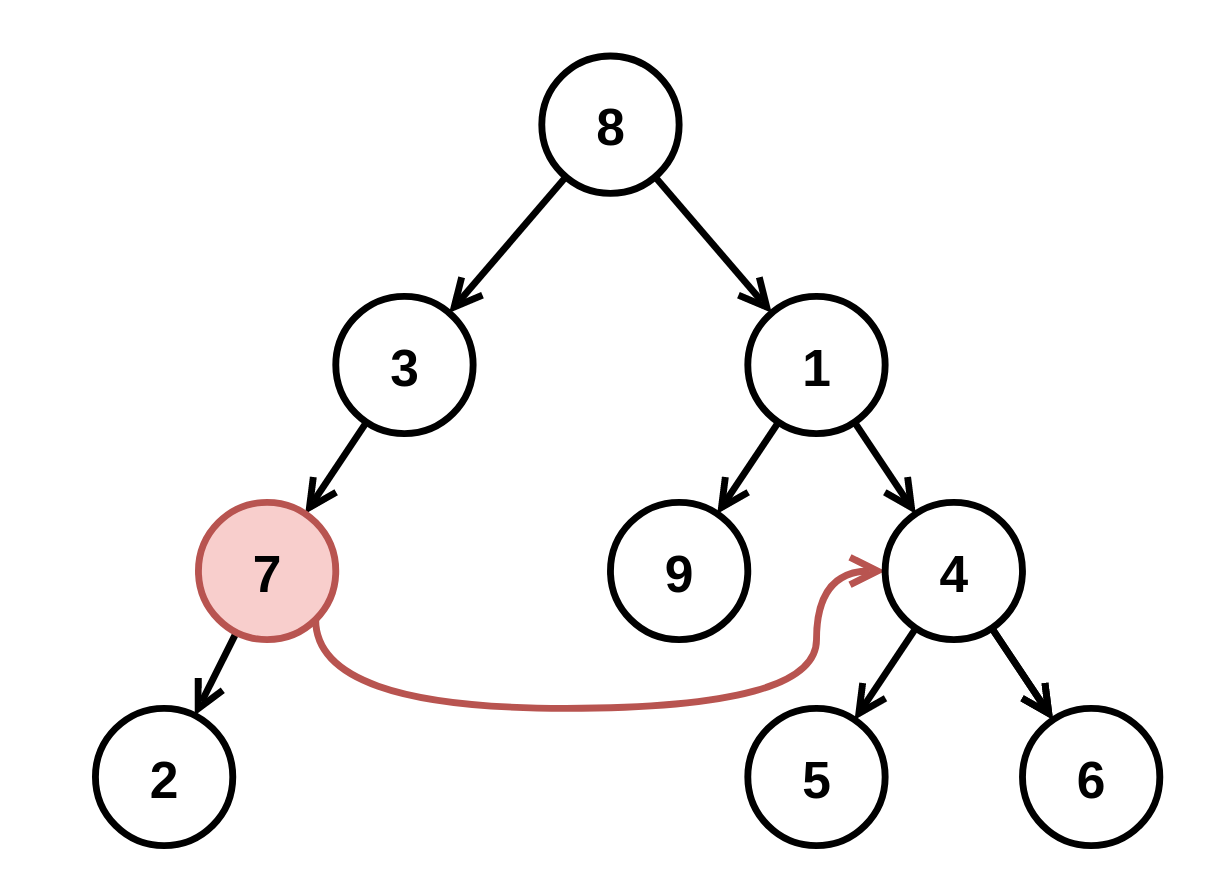
Example 2:

Input: root = [8,3,1,7,null,9,4,2,null,null,null,5,6], fromNode = 7, toNode = 4

Output: [8,3,1,null,null,9,4,null,null,5,6]

Explanation: The node with value 7 is invalid, so remove it and the node underneath it, node 2.

 

Constraints:

• The number of nodes in the tree is in the range [3, 104].
• -109 <= Node.val <= 109
• All Node.val are unique.
• fromNode != toNode
• fromNode and toNode will exist in the tree and will be on the same depth.
• toNode is to the right of fromNode.
• fromNode.right is null in the initial tree from the test data.

Solutions

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def correctBinaryTree(self, root: TreeNode) -> TreeNode:
        q = deque([root])
        res = root
        p = {}
        while q:
            n = len(q)
            mp = {}
            for _ in range(n):
                node = q.popleft()
                if node.val in mp:
                    left, father = p[mp[node.val]]
                    if left:
                        father.left = None
                    else:
                        father.right = None
                    return res
                if node.left:
                    q.append(node.left)
                    p[node.left.val] = [True, node]
                if node.right:
                    q.append(node.right)
                    p[node.right.val] = [False, node]
                    mp[node.right.val] = node.val
        return res

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def correctBinaryTree(self, root: TreeNode) -> TreeNode:
        q = deque([root])
        while q:
            n = len(q)
            for _ in range(n):
                node = q.popleft()
                if node.right:
                    if node.right.right in q:
                        node.right = None
                        return root
                    q.append(node.right)
                if node.left:
                    if node.left.right in q:
                        node.left = None
                        return root
                    q.append(node.left)
        return root

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode correctBinaryTree(TreeNode root) {
        Deque<TreeNode> q = new ArrayDeque<>();
        q.offer(root);
        while (!q.isEmpty()) {
            int n = q.size();
            while (n-- > 0) {
                TreeNode node = q.pollFirst();
                if (node.right != null) {
                    if (node.right.right != null && q.contains(node.right.right)) {
                        node.right = null;
                        return root;
                    }
                    q.offer(node.right);
                }
                if (node.left != null) {
                    if (node.left.right != null && q.contains(node.left.right)) {
                        node.left = null;
                        return root;
                    }
                    q.offer(node.left);
                }
            }
        }
        return root;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* correctBinaryTree(TreeNode* root) {
        queue<TreeNode*> q;
        q.push(root);
        unordered_set<TreeNode*> s;
        while (!q.empty())
        {
            int n = q.size();
            while (n--)
            {
                TreeNode* node = q.front();
                q.pop();
                if (node->right)
                {
                    if (s.count(node->right->right))
                    {
                        node->right = nullptr;
                        return root;
                    }
                    q.push(node->right);
                    s.insert(node->right);
                }
                if (node->left)
                {
                    if (s.count(node->left->right))
                    {
                        node->left = nullptr;
                        return root;
                    }
                    q.push(node->left);
                    s.insert(node->left);
                }
            }
        }
        return root;
    }
};

...