A series of highways connect n cities numbered from 0 to n - 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.
You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway.
Return the minimum total cost to go from city 0 to city n - 1, or -1 if it is not possible to go from city 0 to city n - 1.
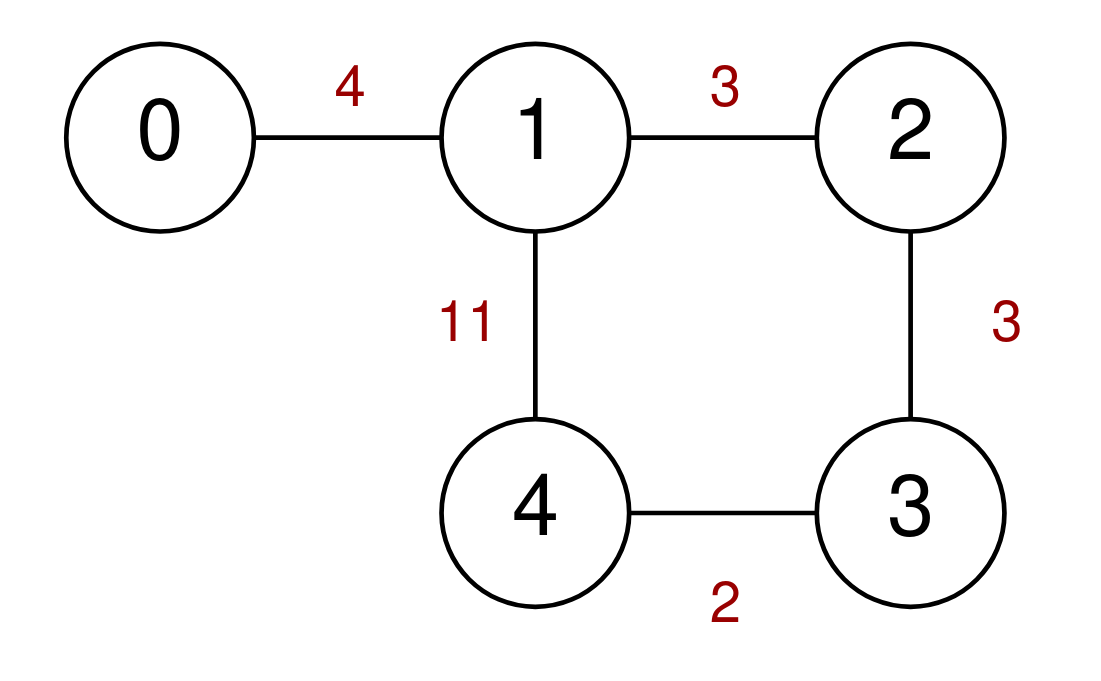
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1 Output: 9 Explanation: Go from 0 to 1 for a cost of 4. Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5. The minimum cost to go from 0 to 4 is 4 + 5 = 9.
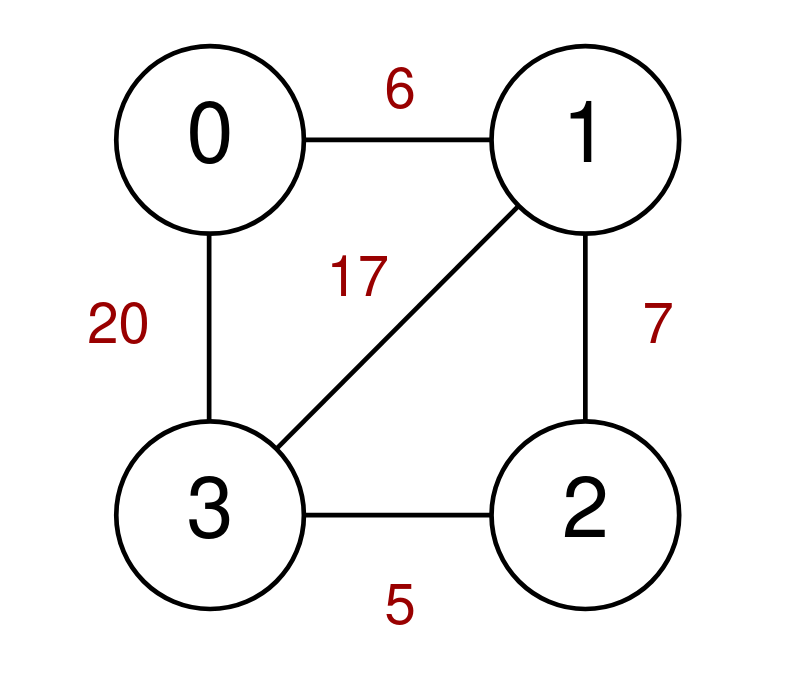
Input: n = 4, highways = [[1,3,17],[1,2,7],[3,2,5],[0,1,6],[3,0,20]], discounts = 20 Output: 8 Explanation: Go from 0 to 1 and use a discount for a cost of 6 / 2 = 3. Go from 1 to 2 and use a discount for a cost of 7 / 2 = 3. Go from 2 to 3 and use a discount for a cost of 5 / 2 = 2. The minimum cost to go from 0 to 3 is 3 + 3 + 2 = 8.
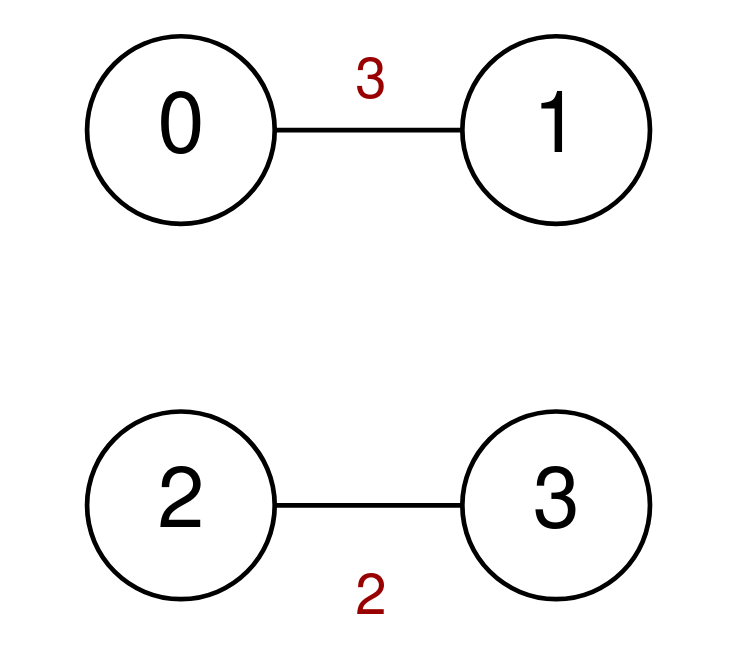
Input: n = 4, highways = [[0,1,3],[2,3,2]], discounts = 0 Output: -1 Explanation: It is impossible to go from 0 to 3 so return -1.
Constraints:
2 <= n <= 10001 <= highways.length <= 1000highways[i].length == 30 <= city1i, city2i <= n - 1city1i != city2i0 <= tolli <= 1050 <= discounts <= 500- There are no duplicate highways.