README.rst

Schrödinger-Poisson solver for 2D materials

Contents

• 1   Introduction
• 2   How to cite
• 3   Try it live!
• 4   How to compile
• 5   How to run
• 6   Description of the input and output files
• 7   Code license

1   Introduction

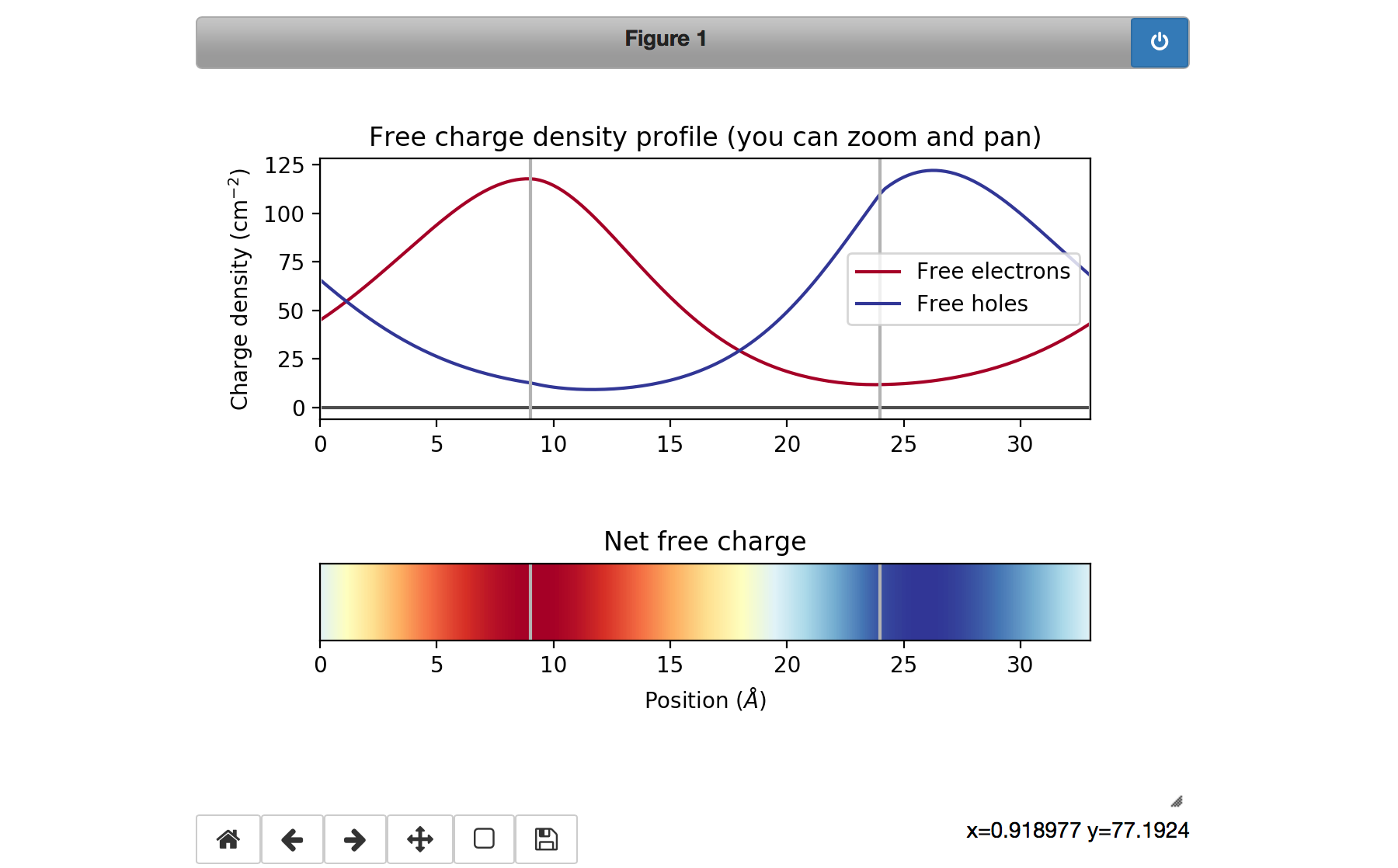
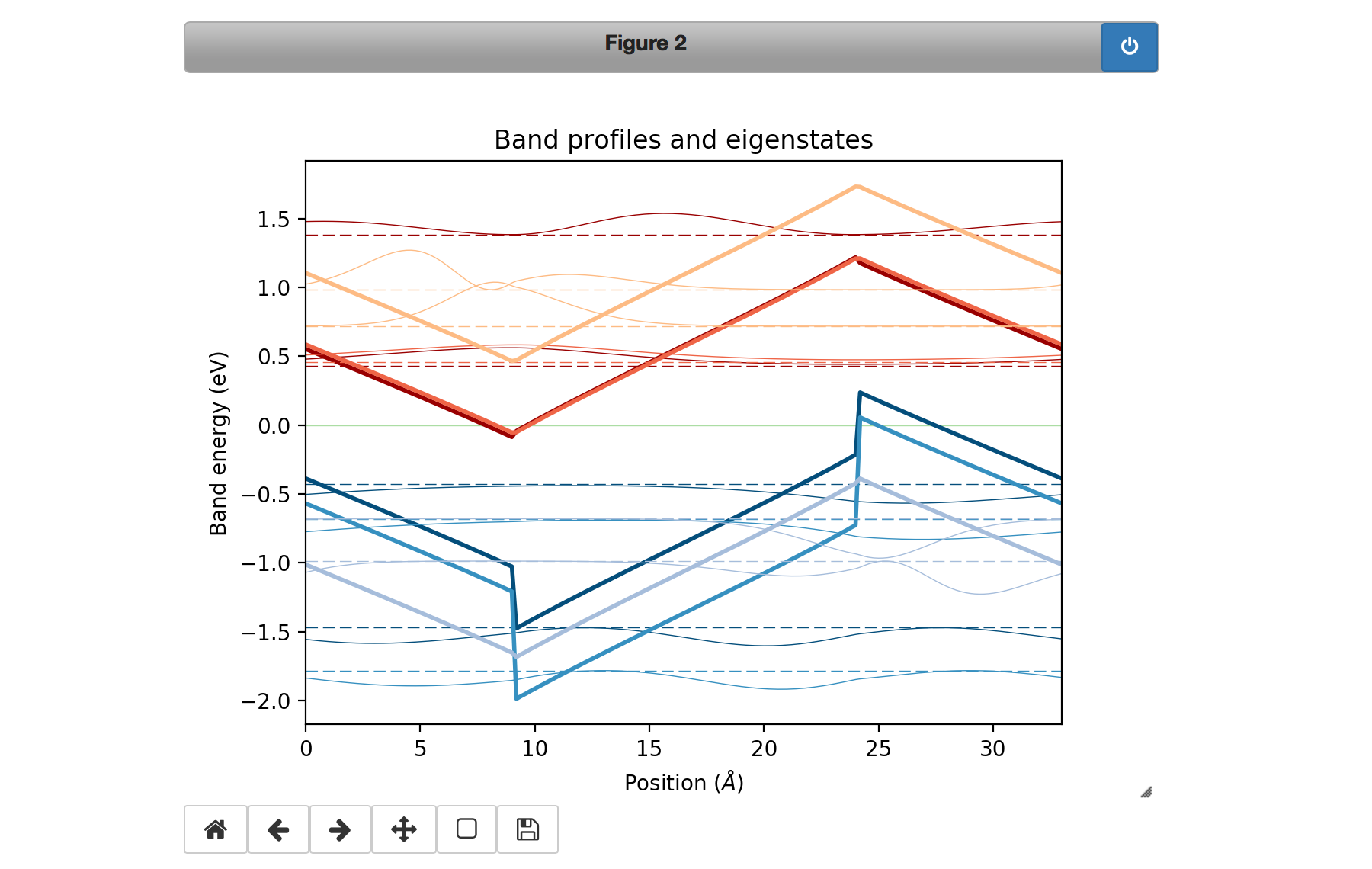
This code aims at self-consistently solving the coupled Schrödinger-Poisson equations in 2D materials. More precisely, in the current implementation it is designed to simulate nanosheets of a single material with regions of different strains. The Schrödinger equation is in 1D, meaning that the strain can vary on a single axis x. Moreover, the material is assumed to be infinite in the y direction and periodic in the x direction.

2   How to cite

If you use this code in your work, please cite the following paper:

• A. Bussy, G. Pizzi, M. Gibertini, Strain-induced polar discontinuities in 2D materials from combined first-principles and Schrödinger-Poisson simulations, Phys. Rev. B 96, 165438 (2017). [DOI] [arXiv]

3   Try it live!

Run the simulation live in your browser (no login required!)

4   How to compile

You first need to have/install some dependencies:

• python
• the python numpy package (this is also needed to have the f2py compiler)
• the python matplotlib package (if you want to interactively show the plots)

You can then compile the Fortran part of the code by simply typing make inside the code folder.

5   How to run

Go into the code folder and run:

python schrpoisson2D.py {material_properties}.json {calc_input}.json

where you need to replace the two command-line options with two valid input files, the first for the materials properties of the system, and the second with the code input flags.

You will find some example input files in the input_examples subfolder.

6   Description of the input and output files

The two input files must be in JSON format and contain all the input needed to specify the system properties and the input flags.

A detailed description of the input flags can be found in the PDF documentation in the docs/compiled_output subfolder, as well as a longer documentation and the description of the output files produced by the code.

7   Code license

The code is released open-source under a MIT license (see LICENSE.txt file).