README.raw.md

Gray Code and Set using Hashtable

[toc]

Introduction

In this task we will use C++ to implement Gray code generation and Set container based on HashTable.

The first section will describe a generic binary data container and give a Gray code implementation based on it.

The second section will describe the collection and its associated operations.

Gray code

Summary

Gray codes are used in some basic applications of signal transmission: in some cases it is unreliable to use traditional binary data transmission, for example:

We need to transfer the data "8" to the target after coding it - it has a binary code of 1000 and assume the current register storage is "7" - the corresponding code is 0111, during this conversion process, the possible register states are:

{ 0110, 0101, 0100, 0011, 0010, 0001, 0000 }

This encoding has a large margin of error when approaching digital transformations, and Gray Code solves this problem.

Gray Code is also known as "Least Difference Code" because the binary digits of two adjacent numbers differ by only one digit.

Because the mapping from Binary codes set to Gray codes set is Injection, which means: assume $n$ bits Binary codes set is $X$, corresponding Gray codes set is $Y$, the conversion function from binary to Gray codes is $f: X \to Y$, so we got: $$ \forall x \in X ,; \exist f(x) = y \in Y\ \forall x, x' \in X ,; f(x) = f(x') \Rightarrow x = x' $$ So the total number of $n$ bits of the Gray code is $2^n$, which equal to $n$ bits of Binary codes.

Construction

We will give three ways of generating $n$ bits Gray codes and explain the principles behind them.

Manual calculation

Starting with the binary number $0$, repeat $2^n - 1$ times to construct all the Gray codes of the $n$ bit, following the pattern below:

• Change the value of the rightmost bit
• Changes the left bit of the first bit from the right that is $1$

This method is more complex and we usually use the following two methods for construction.

Recursive construction

According to the above construction of the Gray code, it is easy to see that the Gray code has a certain symmetrical structure, take $3$ bits Gray Code for example: $$ 0 ; 00 \ 0 ; 01 \ 0 ; 11 \ 0 ; 10 \ --- \ 1 ; 10 \ 1 ; 11 \ 1 ; 01 \ 1 ; 00 $$ A more visual explanation:

Except of the highest bit $0,1$, the next two bits which above and below the dividing line are symmetrical, which means:

Every $n$ bits Gray Code can be constructed by $n-1$ bit Gray Code.

It can be operated as an Recusive program, fake-code below:

def GrayCode(power: int) -> List[String, 2 ** power]:
  
  # Termination conditions
  if (n == 1) return ["0", "1"]

  codes = List[String, 2 ** power]
  before: List[String, 2 ** (power - 1)] = GrayCode(n - 1)
  for code in before:
    codes.append("1" + code)
    
  for code in before[::-1]:
    codes.append("0" + code)
    
  return codes

Calculate construction

We can construct Gray codes from decimal numbers with the following function:

unsigned int g(unsigned int) { return n^(n >> 1); }

And we could prove that in the Gray Code sequence generated according to the above function, the binary bits of two adjacent Gray codes have only one bit difference.

Considering about the diffrence between $n$ and $n + 1$. Add up 1 to $n$ equaivalent to changing all the consecutive $1$ bits into $0$, which is inverting. Then change the lowest bit from $0$ to $1$: $$ \begin{aligned} (n)2 &= \dots 0 \overbrace{11\cdots 11}^{k \text{ times}} \ (n + 1)2 &= \dots 1 \underbrace{00 \cdots 00}{k \text{ times}} \end{aligned} $$ So when we calculaing $g(n)$ and $g(n + 1)$, the last $k$ bits will be: $$ \underbrace{100 \cdots 00}{k \text{ times}} $$ and the $k + 1$ bits is different. Because $n$ and $n+1$ are the same except for the last $k+1$ bits, therefore, the $k+1$ bit is either XORed by $1$ at the same time, or XORed by $0$ at the same time. In both cases, the $k+1$ bit is different. The binary bits except the last $k+1$ bits are also subjected to the same XOR operation, and the result is the same.

Binary encoding container

We use bytes as the smallest container storage unit, which corresponds to unsigned char in the C++ type system. Since the smallest unit of operation in c++ is byte, we need to use bit operators to operate on different bits.

Container

We use an unsigned char array to store bit information.

Its length is uniform on each platform - 1 byte. And when we need to set a bit, we find the specified byte variable through the index of the operation firstly. Then perform bit manipulation, which is write down below.

Bit write operation

To write a bit, we need to judge in two situations:

• Write a 1 bit

  Assume we need to set a specific bit to 1, it can be performed by OR operation before raw bits with bits 0000...1...0, which position of 1 is index we need to set.

• Write a 0 bit

  To write 0 to bits, we could using AND bits operation between raw bits and bits set 1111...0...1, which position of 0 is index we need to set.

Bit read operation

When we need to read a specified bit, we can use the AND bit operator to perform operations between the original bit string and 0000...1...0, then shift the obtained value to the right and the bit to the right The number is defined by the index of the number of digits read. The Boolean type conversion of the value obtained in this way is the result we need.

Gray code

The Binary class defined in this way can be used directly as the Gray Code class. In order to add the function of generating Gray codes from decimal numbers, we use class inheritance and add the import method:

class Gray: public Binary {
public:
    using Binary::Binary;

public:
    template <typename VT>
    void import(VT value) {
        this->decimal<VT>(value ^ (value >> 1));
    }
};

Set

In mathematics, a set is a well-defined collection of distinct objects, considered as an object in its own right.The arrangement of the objects in the set does not matter. A set may be denoted by placing its objects between a pair of curly braces.

Typically, the same element can only appear once in the same set. In contrast, the notion of Multiple sets can be used if multiple occurrences of the same element in a set required.

Binary operations among sets

Given two sets $A$ and $B$, define the operation between them:

• Union $$ A \cup B = {x | x \in A \or x \in B } $$

• Intersection $$ A \cap B = {x | x \in A \and x \in B } $$

• Complement, assume $U$ is universal set $$ \bar{A} = { x | x \notin A } $$

• Difference $$ A - B = { x | x \in A \and x \notin B } $$

• Symmetric Difference $$ A \Delta B = (A - B) \cup (B - A) $$

Hash Table

Summary

The data structure of Set is implememted using a Hash Table. Inside the hash table, a Vector based on a linked list is used as a slot to store data to resolve conflicts.

Hash table is used in situations where it is necessary to quickly determine whether a given element exists in the data container. In some cases, it can be modified to implement a Ditionary.

We refer to the data stored in the hash table as element.

The basic idea of hash table is as follows:

0. Allocate for a certain space in advance and number different positions in the space
1. Use a function to calculate a hash value for a given element
2. Using the calculated hash value as the location, store the given element in the corresponding location
3. When we need to judge whether an element is in the hash table, perform the hash function on it, and check whether the element exists at the obtained position.

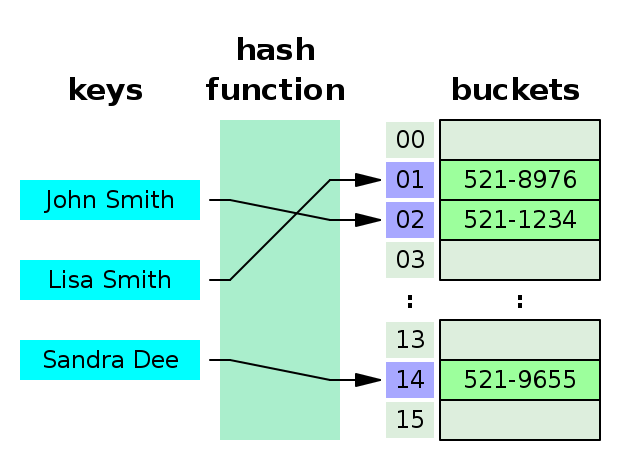
Here is an exaple of Hash table using given key for calculation of hash value, which is like Dictionary:

Before using the hash table, we need to provide an estimate of the size of the hash table: when the size of the hash table is too small and the amount of data used is large, it will cause a lot of conflicts, which will cause performance degradation.

The set here can implement multiple sets and normal sets at the same time.

For a Gray code with $n$ bits, the size of the global set $S$ can be easily calculated using the following formula: $$ S = 2^n $$ Using C++ template-based programming, we can specify different hash functions for different types.

Vector

We use linked list to implement Vector as a data container. The linked list here refers to a singly linked list-that is, each node only stores the pointer and data of the next node.

Simple of Linked list here:

The reason for using linked lists is that we cannot determine how many items need to be stored in each slot. Querying nodes in the linked list needs to start from the beginning, traversing the value of each node for comparison. Although the data is obviously too concentrated, it will cause a significant drop in performance.

Our implementation of Node is as follows:

template <typename T>
class Node {
public:
    T* _data;
    Node* _next;

public:
    Node() = delete;
    explicit Node(const T& value) {
        this->_data = new T(value);
        this->_next = nullptr;
    }
    bool isend() const { return (this->_next == nullptr); }
    const T& value() { return *this->_data; }
    ~Node() { free(this->_data); }
};

Based on this we can implement a linked list:

template <typename T>
class Vector {
private:
    size_t _size;
    Node<T>* _header;

public:
    Vector(): _size(0), _header(nullptr) {}
    size_t count() const { return this->_size; }
    const T& get(size_t index);
    bool empty() const;
    bool exist(const T& value) const;
    void remove(const T& value);
    T& index(size_t index);
    T pop(size_t index);
}

The time complexity table of the methods:

Method	Complexity
count	$O(1)$
get	$O(n)$
empty	$O(1)$
exist	$O(n)$
remove	$O(n)$
index	$O(n)$
pop	$O(n)$

Hash Function

According to the above description, it can be found that the hash function will greatly affect the performance of the hash table:

• If the value of the function is too concentrated, it will increase conflicts and cause performance degradation
• If the function is too complex, it will increase the time of each element operation

And since our task is to store the Gray code in the set, according to the description above, there is a one-to-one correspondence between binary and decimal, we can directly use the gray code corresponding to the decimal value as the hash value:

template <>
unsigned int hash<Gray>(size_t maxsize, const Gray& bin) {
    return bin.decimal() % maxsize;
}

Here, the function template specialization is used to define the gray code type hash function, and in order to ensure that the hash value does not exceed the maximum range of the hash table, the first parameter of the hash function specifies the capacity of the hash table, use % modulates the calculated value.

Collision

It can be seen that when two elements have the same hash value, a collision will occur. At this time, we can use a linked list to store the colliding elements in order:

We call the linked list corresponding to each address a slot.

Traversal

When we need to traverse the elements in the hash table, we use an iterator type instance to save the current traversed slot index; at the same time, because each slot may have more than one element, we need another member to save the current slot internal index:

class Iterator {
    private:
        Vector<T>** _slots;
        size_t _current;
        size_t _index;
        size_t _size;
        ...
}

In the process of traversal, the internal member variables are updated, and the pointed slot can be changed.

At the same time, you can add begin, end methods to the collection to support the range-based for loop in the C++14 standard.

Implementation and performance analysis

In implementation, before adding an element, we can selectively check whether the current collection has this element in method add:

• Check to ensure that all elements in the table are not the same - Set
• You can store multiple identical elements in the same table without checking - Multiple Set

template <typename T>
unsigned int hash(size_t, const T&);

template <typename T>
class Set {
private:
    size_t _size;
    Vector<T>** _slots;
    size_t _count;
    bool _unique;

public:
    size_t count() const;
    void add(const T& value);
    void remove(const T& value);
    bool in(const T& value) const;
}

The time complexity table of the methods:

Method	Average	Worst Case
count	$O(1)$	$O(1)$
add	$O(1)$	$O(n)$
in	$O(1)$	$O(n)$
remove	$O(!)$	$O(n)$