递归行为的实质和递归行为时间复杂度的计算.md

递归行为的实质和递归行为时间复杂度的计算

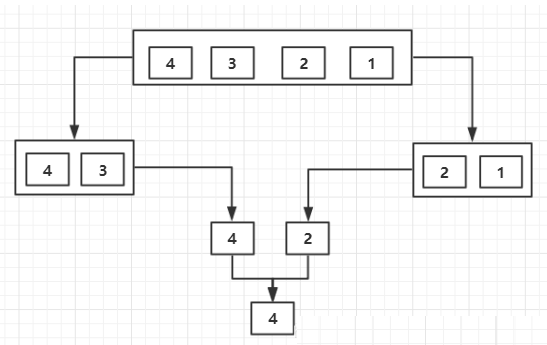
任何非递归都可以改成递归

递归行为的实质

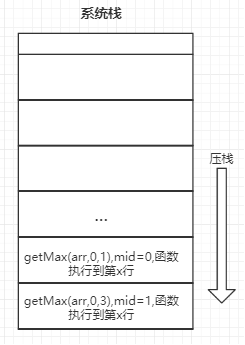
递归是指自己调用自己(子过程), 当调用子过程的时候, 将当前程序执行状态(包括参数信息、变量信息、程序执行到第几行等)压栈,
直到有返回的时候, 从栈顶将程序执行状态出栈, 彻底还原调用子过程之前的现场.

一个递归行为的例子

java

public class Recursion {
	/**
	 * 通过递归求数组最大值
	 * @param arr
	 * @param left
	 * @param right
	 * @return
	 */
	public static int getMax(int[] arr, int left, int right) {
		if (left == right) {
			return arr[left];
		}
		
		int mid = (left + right) / 2;
		System.out.println(mid); 
		int maxLeft = getMax(arr, left, mid);
		int maxRight = getMax(arr, mid + 1, right);
		
		return Math.max(maxLeft, maxRight);
	}
	
	public static void main(String[] args) {
		int[] arr = {4, 3, 2, 1};
		System.out.println(getMax(arr, 0, arr.length - 1));
	}
}

递归执行的流程描述

getMax(arr, 0, 3) mid = 1                                               ---1
    int maxLeft = getMax(arr, 0, 1) mid = 0                             ---2
        int maxLeft = getMax(arr, 0, 0) return arr[0]                   ---3
        int maxRight = getMax(arr, 1, 1) return arr[1]                  ---4
        return max(maxLeft, maxRight) = arr[0]                          ---5
    
    int maxRight = getMax(arr, 2, 3) mid = 2                            ---6
        int maxLeft = getMax(arr, 2, 2) return arr[2]                   ---7
        int maxRight = getMax(arr, 3, 3) return arr[3]                  ---8
        return max(maxLeft, maxRight) = arr[2]                          ---9
    
    return max(maxLeft, maxRight) = max(arr[0], arr[2]) = max(4, 2)     ---10

递归执行的流程图解

递归执行的原理

当执行到2时, 
    将1中的程序执行状态(包括参数信息、变量信息、程序执行到第几行等)压栈
当执行到3时, 
    将2中的程序执行状态压栈, 直到3 return arr[0] , 将2中的程序执行状态出栈, 继续执行2中程序中的下一行代码, 即执行4
当执行到4时, 
    将2中的程序执行状态压栈, 直到4 return arr[1] , 将2中的程序执行状态出栈, 继续执行2中程序中的下一行代码, 即执行5    
执行完5后, return max(maxLeft, maxRight) = arr[0], 将1中的程序执行状态出栈, 继续执行1中程序的下一行代码, 即执行6
...

压栈

递归行为时间复杂度的计算

master公式: T(N) = a*T(N/b) + O(N^d)

N为总样本量
a为子过程发生的次数
N/b为子过程的样本量
N^d为除了调用子过程外其他操作所花费的时间

在上述例子中

子过程的样本量是N/2, 所以b=2
一个过程分为两个子过程, 一个子过程又分为两个子过程, 所以a=2
除了调用子过程外其他操作所花费的时间为O(1), 所以d=0

T(N) = 2*T(N/2) + O(1)

如何求解复杂度?

1) log(b,a) > d 复杂度为O(N^log(b,a))
2) log(b,a) = d 复杂度为O(N^d * logN)
3) log(b,a) < d 复杂度为O(N^d)

因为在上述例子中, log(2, 2) = 1 > d = 0, 所以复杂度为 O(N^log(2,2)) = O(N)