diff --git a/.all-contributorsrc b/.all-contributorsrc
index ec7ff5a1c..05e429904 100644
--- a/.all-contributorsrc
+++ b/.all-contributorsrc
@@ -7,10 +7,19 @@
],
"contributors": [
{
- "login": "ShvetankPrakash",
- "name": "Shvetank Prakash",
- "avatar_url": "https://avatars.githubusercontent.com/ShvetankPrakash",
- "profile": "https://github.com/ShvetankPrakash",
+ "login": "Mjrovai",
+ "name": "Marcelo Rovai",
+ "avatar_url": "https://avatars.githubusercontent.com/Mjrovai",
+ "profile": "https://github.com/Mjrovai",
+ "contributions": [
+ "doc"
+ ]
+ },
+ {
+ "login": "ishapira1",
+ "name": "ishapira",
+ "avatar_url": "https://avatars.githubusercontent.com/ishapira1",
+ "profile": "https://github.com/ishapira1",
"contributions": [
"doc"
]
@@ -25,118 +34,118 @@
]
},
{
- "login": "sjohri20",
- "name": "sjohri20",
- "avatar_url": "https://avatars.githubusercontent.com/sjohri20",
- "profile": "https://github.com/sjohri20",
+ "login": "18jeffreyma",
+ "name": "Jeffrey Ma",
+ "avatar_url": "https://avatars.githubusercontent.com/18jeffreyma",
+ "profile": "https://github.com/18jeffreyma",
"contributions": [
"doc"
]
},
{
- "login": "jaysonzlin",
- "name": "Jayson Lin",
- "avatar_url": "https://avatars.githubusercontent.com/jaysonzlin",
- "profile": "https://github.com/jaysonzlin",
+ "login": "uchendui",
+ "name": "Ikechukwu Uchendu",
+ "avatar_url": "https://avatars.githubusercontent.com/uchendui",
+ "profile": "https://github.com/uchendui",
"contributions": [
"doc"
]
},
{
- "login": "BaeHenryS",
- "name": "Henry Bae",
- "avatar_url": "https://avatars.githubusercontent.com/BaeHenryS",
- "profile": "https://github.com/BaeHenryS",
+ "login": "sophiacho1",
+ "name": "sophiacho1",
+ "avatar_url": "https://avatars.githubusercontent.com/sophiacho1",
+ "profile": "https://github.com/sophiacho1",
"contributions": [
"doc"
]
},
{
- "login": "Naeemkh",
- "name": "naeemkh",
- "avatar_url": "https://avatars.githubusercontent.com/Naeemkh",
- "profile": "https://github.com/Naeemkh",
+ "login": "ShvetankPrakash",
+ "name": "Shvetank Prakash",
+ "avatar_url": "https://avatars.githubusercontent.com/ShvetankPrakash",
+ "profile": "https://github.com/ShvetankPrakash",
"contributions": [
"doc"
]
},
{
- "login": "mmaz",
- "name": "Mark Mazumder",
- "avatar_url": "https://avatars.githubusercontent.com/mmaz",
- "profile": "https://github.com/mmaz",
+ "login": "mpstewart1",
+ "name": "Matthew Stewart",
+ "avatar_url": "https://avatars.githubusercontent.com/mpstewart1",
+ "profile": "https://github.com/mpstewart1",
"contributions": [
"doc"
]
},
{
- "login": "18jeffreyma",
- "name": "Jeffrey Ma",
- "avatar_url": "https://avatars.githubusercontent.com/18jeffreyma",
- "profile": "https://github.com/18jeffreyma",
+ "login": "Naeemkh",
+ "name": "naeemkh",
+ "avatar_url": "https://avatars.githubusercontent.com/Naeemkh",
+ "profile": "https://github.com/Naeemkh",
"contributions": [
"doc"
]
},
{
- "login": "uchendui",
- "name": "Ikechukwu Uchendu",
- "avatar_url": "https://avatars.githubusercontent.com/uchendui",
- "profile": "https://github.com/uchendui",
+ "login": "profvjreddi",
+ "name": "Vijay Janapa Reddi",
+ "avatar_url": "https://avatars.githubusercontent.com/profvjreddi",
+ "profile": "https://github.com/profvjreddi",
"contributions": [
"doc"
]
},
{
- "login": "jessicaquaye",
- "name": "Jessica Quaye",
- "avatar_url": "https://avatars.githubusercontent.com/jessicaquaye",
- "profile": "https://github.com/jessicaquaye",
+ "login": "mmaz",
+ "name": "Mark Mazumder",
+ "avatar_url": "https://avatars.githubusercontent.com/mmaz",
+ "profile": "https://github.com/mmaz",
"contributions": [
"doc"
]
},
{
- "login": "DivyaAmirtharaj",
- "name": "Divya",
- "avatar_url": "https://avatars.githubusercontent.com/DivyaAmirtharaj",
- "profile": "https://github.com/DivyaAmirtharaj",
+ "login": "BaeHenryS",
+ "name": "Henry Bae",
+ "avatar_url": "https://avatars.githubusercontent.com/BaeHenryS",
+ "profile": "https://github.com/BaeHenryS",
"contributions": [
"doc"
]
},
{
- "login": "mpstewart1",
- "name": "Matthew Stewart",
- "avatar_url": "https://avatars.githubusercontent.com/mpstewart1",
- "profile": "https://github.com/mpstewart1",
+ "login": "oishib",
+ "name": "oishib",
+ "avatar_url": "https://avatars.githubusercontent.com/oishib",
+ "profile": "https://github.com/oishib",
"contributions": [
"doc"
]
},
{
- "login": "Mjrovai",
- "name": "Marcelo Rovai",
- "avatar_url": "https://avatars.githubusercontent.com/Mjrovai",
- "profile": "https://github.com/Mjrovai",
+ "login": "marcozennaro",
+ "name": "Marco Zennaro",
+ "avatar_url": "https://avatars.githubusercontent.com/marcozennaro",
+ "profile": "https://github.com/marcozennaro",
"contributions": [
"doc"
]
},
{
- "login": "oishib",
- "name": "oishib",
- "avatar_url": "https://avatars.githubusercontent.com/oishib",
- "profile": "https://github.com/oishib",
+ "login": "jessicaquaye",
+ "name": "Jessica Quaye",
+ "avatar_url": "https://avatars.githubusercontent.com/jessicaquaye",
+ "profile": "https://github.com/jessicaquaye",
"contributions": [
"doc"
]
},
{
- "login": "profvjreddi",
- "name": "Vijay Janapa Reddi",
- "avatar_url": "https://avatars.githubusercontent.com/profvjreddi",
- "profile": "https://github.com/profvjreddi",
+ "login": "sjohri20",
+ "name": "sjohri20",
+ "avatar_url": "https://avatars.githubusercontent.com/sjohri20",
+ "profile": "https://github.com/sjohri20",
"contributions": [
"doc"
]
@@ -151,28 +160,19 @@
]
},
{
- "login": "marcozennaro",
- "name": "Marco Zennaro",
- "avatar_url": "https://avatars.githubusercontent.com/marcozennaro",
- "profile": "https://github.com/marcozennaro",
- "contributions": [
- "doc"
- ]
- },
- {
- "login": "ishapira1",
- "name": "ishapira",
- "avatar_url": "https://avatars.githubusercontent.com/ishapira1",
- "profile": "https://github.com/ishapira1",
+ "login": "jaysonzlin",
+ "name": "Jayson Lin",
+ "avatar_url": "https://avatars.githubusercontent.com/jaysonzlin",
+ "profile": "https://github.com/jaysonzlin",
"contributions": [
"doc"
]
},
{
- "login": "sophiacho1",
- "name": "sophiacho1",
- "avatar_url": "https://avatars.githubusercontent.com/sophiacho1",
- "profile": "https://github.com/sophiacho1",
+ "login": "DivyaAmirtharaj",
+ "name": "Divya",
+ "avatar_url": "https://avatars.githubusercontent.com/DivyaAmirtharaj",
+ "profile": "https://github.com/DivyaAmirtharaj",
"contributions": [
"doc"
]
diff --git a/README.md b/README.md
index 3519e09c2..9dec61d9a 100644
--- a/README.md
+++ b/README.md
@@ -88,31 +88,31 @@ quarto render
diff --git a/contributors.qmd b/contributors.qmd
index 24df99e18..37d013133 100644
--- a/contributors.qmd
+++ b/contributors.qmd
@@ -8,31 +8,31 @@ We extend our sincere thanks to the diverse group of individuals who have genero
diff --git a/images/efficientnumerics_PTQQATsummary.png b/images/efficientnumerics_PTQQATsummary.png
index bf1ba26ef..3d950998b 100644
Binary files a/images/efficientnumerics_PTQQATsummary.png and b/images/efficientnumerics_PTQQATsummary.png differ
diff --git a/images/efficientnumerics_alexnet.png b/images/efficientnumerics_alexnet.png
index 74bf5c950..be44cb78c 100644
Binary files a/images/efficientnumerics_alexnet.png and b/images/efficientnumerics_alexnet.png differ
diff --git a/images/efficientnumerics_benefitsofprecision.png b/images/efficientnumerics_benefitsofprecision.png
index 9ac3e811a..210f5abfb 100644
Binary files a/images/efficientnumerics_benefitsofprecision.png and b/images/efficientnumerics_benefitsofprecision.png differ
diff --git a/images/efficientnumerics_calibration.png b/images/efficientnumerics_calibration.png
index e37f858bf..76de8ff43 100644
Binary files a/images/efficientnumerics_calibration.png and b/images/efficientnumerics_calibration.png differ
diff --git a/images/efficientnumerics_calibrationcopy.png b/images/efficientnumerics_calibrationcopy.png
new file mode 100644
index 000000000..76de8ff43
Binary files /dev/null and b/images/efficientnumerics_calibrationcopy.png differ
diff --git a/images/efficientnumerics_edgequant.png b/images/efficientnumerics_edgequant.png
index 71d278bb9..ea136f2a4 100644
Binary files a/images/efficientnumerics_edgequant.png and b/images/efficientnumerics_edgequant.png differ
diff --git a/images/efficientnumerics_modelsizes.png b/images/efficientnumerics_modelsizes.png
index 8d6aa902c..5dad5fbce 100644
Binary files a/images/efficientnumerics_modelsizes.png and b/images/efficientnumerics_modelsizes.png differ
diff --git a/images/efficientnumerics_qp1.png b/images/efficientnumerics_qp1.png
index 9862a00db..9d9596344 100644
Binary files a/images/efficientnumerics_qp1.png and b/images/efficientnumerics_qp1.png differ
diff --git a/images/efficientnumerics_qp2.png b/images/efficientnumerics_qp2.png
index a3b799cfc..e8ee6442f 100644
Binary files a/images/efficientnumerics_qp2.png and b/images/efficientnumerics_qp2.png differ
diff --git a/images/modeloptimization_color_mappings.jpeg b/images/modeloptimization_color_mappings.jpeg
new file mode 100644
index 000000000..0531a9d8c
Binary files /dev/null and b/images/modeloptimization_color_mappings.jpeg differ
diff --git a/images/modeloptimization_onnx.jpg b/images/modeloptimization_onnx.jpg
new file mode 100644
index 000000000..e5218a9c3
Binary files /dev/null and b/images/modeloptimization_onnx.jpg differ
diff --git a/images/modeloptimization_quant_hist.png b/images/modeloptimization_quant_hist.png
new file mode 100644
index 000000000..a9cdff8e1
Binary files /dev/null and b/images/modeloptimization_quant_hist.png differ
diff --git a/optimizations.qmd b/optimizations.qmd
index 5c4e246a7..cdb9c346c 100644
--- a/optimizations.qmd
+++ b/optimizations.qmd
@@ -29,7 +29,7 @@ Going one level lower, in @sec-model_ops_numerics, we study the role of numerica
Finally, as we go lower closer to the hardware, in @sec-model_ops_hw, we will navigate through the landscape of hardware-software co-design, exploring how models can be optimized by tailoring them to the specific characteristics and capabilities of the target hardware. We will discuss how models can be adapted to exploit the available hardware resources effectively.
-
+{width=50%}
## Efficient Model Representation {#sec-model_ops_representation}
@@ -55,7 +55,7 @@ So how does one choose the type of pruning methods? Many variations of pruning t
#### Structured Pruning
-We start with structured pruning, a technique that reduces the size of a neural network by eliminating entire model-specific substructures while maintaining the overall model structure. It removes entire neurons/filters or layers based on importance criteria. For example, for a convolutional neural network (CNN), this could be certain filter instances or channels. For fully connected networks, this could be neurons themselves while maintaining full connectivity or even be elimination of entire model layers that are deemed to be insignificant. This type of pruning often leads to regular, structured sparse networks that are hardware friendly.
+We start with structured pruning, a technique that reduces the size of a neural network by eliminating entire model-specific substructures while maintaining the overall model structure. It removes entire neurons/channels or layers based on importance criteria. For example, for a convolutional neural network (CNN), this could be certain filter instances or channels. For fully connected networks, this could be neurons themselves while maintaining full connectivity or even be elimination of entire model layers that are deemed to be insignificant. This type of pruning often leads to regular, structured sparse networks that are hardware friendly.
##### Components
@@ -69,7 +69,7 @@ Best practices have started to emerge on how to think about structured pruning.
Given that there are different strategies, each of these structures (i.e., neurons, channels and layers) is pruned based on specific criteria and strategies, ensuring that the reduced model maintains as much of the predictive prowess of the original model as possible while gaining in computational efficiency and reduction in size.
-The primary structures targeted for pruning include **neurons** , channels, and sometimes, entire layers, each having its unique implications and methodologies. When neurons are pruned, we are removing entire neurons along with their associated weights and biases, thereby reducing the width of the layer. This type of pruning is often utilized in fully connected layers.
+The primary structures targeted for pruning include **neurons**, channels, and sometimes, entire layers, each having its unique implications and methodologies. When neurons are pruned, we are removing entire neurons along with their associated weights and biases, thereby reducing the width of the layer. This type of pruning is often utilized in fully connected layers.
With **channel** pruning, which is predominantly applied in convolutional neural networks (CNNs), it involves eliminating entire channels or filters, which in turn reduces the depth of the feature maps and impacts the network's ability to extract certain features from the input data. This is particularly crucial in image processing tasks where computational efficiency is paramount.
@@ -120,7 +120,7 @@ The pruned model, while smaller, retains its original architectural form, which
Unstructured pruning is, as its name suggests, pruning the model without regard to model-specific substructure. As mentioned above, it offers a greater aggression in pruning and can achieve higher model sparsities while maintaining accuracy given less constraints on what can and can't be pruned. Generally, post-training unstructured pruning consists of an importance criterion for individual model parameters/weights, pruning/removal of weights that fall below the criteria, and optional fine-tuning after to try and recover the accuracy lost during weight removal.
-Unstructured pruning has some advantages over structured pruning: removing individual weights instead of entire model substructures often leads in practice to lower model accuracy hits. Furthermore, generally determining the criterion of importance for an individual weight is much simpler than for an entire substructure of parameters in structured pruning, making the former preferable for cases where that overhead is hard or unclear to compute. Similarly, the actual process of structured pruning is generally less flexible, as removing individual weights is generally simpler than removing entire substructures and ensuring the model still works.
+Unstructured pruning has some advantages over structured pruning: removing individual weights instead of entire model substructures often leads in practice to lower model accuracy decreases. Furthermore, generally determining the criterion of importance for an individual weight is much simpler than for an entire substructure of parameters in structured pruning, making the former preferable for cases where that overhead is hard or unclear to compute. Similarly, the actual process of structured pruning is generally less flexible, as removing individual weights is generally simpler than removing entire substructures and ensuring the model still works.
Unstructured pruning, while offering the potential for significant model size reduction and enhanced deployability, brings with it challenges related to managing sparse representations and ensuring computational efficiency. It is particularly useful in scenarios where achieving the highest possible model compression is paramount and where the deployment environment can handle sparse computations efficiently.
@@ -136,22 +136,22 @@ The following compact table provides a concise comparison between structured and
| **Implementation Complexity**| Often simpler to implement and manage due to maintaining network structure. | Can be complex to manage and compute due to sparse representations. |
| **Fine-Tuning Complexity** | May require less complex fine-tuning strategies post-pruning. | Might necessitate more complex retraining or fine-tuning strategies post-pruning. |
-
+
#### Lottery Ticket Hypothesis
Pruning has evolved from a purely post-training technique that came at the cost of some accuracy, to a powerful meta-learning approach applied during training to reduce model complexity. This advancement in turn improves compute, memory, and latency efficiency at both training and inference.
-A breakthrough finding that catalyzed this evolution was the [lottery ticket hypothesis](https://arxiv.org/abs/1803.03635) empirically discovered by Jonathan Frankle and Michael Carbin. Their work states that within dense neural networks, there exist sparse subnetworks, referred to as "winning tickets," that can match or even exceed the performance of the original model when trained in isolation. Specifically, these winning tickets, when initialized using the same weights as the original network, can achieve similarly high training convergence and accuracy on a given task. It is worthwhile pointing out that they empirically discovered the lottery ticket hypothesis, which was later formalized.
+A breakthrough finding that catalyzed this evolution was the [lottery ticket hypothesis](https://arxiv.org/abs/1803.03635) by @frankle_lottery_2019. They empirically discovered by Jonathan Frankle and Michael Carbin. Their work states that within dense neural networks, there exist sparse subnetworks, referred to as "winning tickets," that can match or even exceed the performance of the original model when trained in isolation. Specifically, these winning tickets, when initialized using the same weights as the original network, can achieve similarly high training convergence and accuracy on a given task. It is worthwhile pointing out that they empirically discovered the lottery ticket hypothesis, which was later formalized.
-More formally, the lottery ticket hypothesis is a concept in deep learning that suggests that within a neural network, there exist sparse subnetworks (or "winning tickets") that, when initialized with the right weights, are capable of achieving high training convergence and inference performance on a given task. The intuition behind this hypothesis is that, during the training process of a neural network, many neurons and connections become redundant or unimportant, particularly with the inclusion of training techniques encouraging redundancy like dropout. Identifying, pruning out, and initializing these "winning tickets'' allows for faster training and more efficient models, as they contain the essential model decision information for the task. Furthermore, as generally known with the bias-variance tradeoff theory, these tickets suffer less from overparameterization and thus generalize better rather than overfitting to the task. 
+More formally, the lottery ticket hypothesis is a concept in deep learning that suggests that within a neural network, there exist sparse subnetworks (or "winning tickets") that, when initialized with the right weights, are capable of achieving high training convergence and inference performance on a given task. The intuition behind this hypothesis is that, during the training process of a neural network, many neurons and connections become redundant or unimportant, particularly with the inclusion of training techniques encouraging redundancy like dropout. Identifying, pruning out, and initializing these "winning tickets'' allows for faster training and more efficient models, as they contain the essential model decision information for the task. Furthermore, as generally known with the bias-variance tradeoff theory, these tickets suffer less from overparameterization and thus generalize better rather than overfitting to the task.
-
+
#### Challenges & Limitations
-There is no free lunch with pruning optimizations.
+There is no free lunch with pruning optimizations, with some choices coming with wboth improvements and costs to considers. Below we discuss some tradeoffs for practitioners to consider.
##### Quality vs. Size Reduction
@@ -187,7 +187,7 @@ Model compression techniques are crucial for deploying deep learning models on r
#### Knowledge Distillation {#sec-kd}
-One popular technique is knowledge distillation (KD), which transfers knowledge from a large, complex "teacher" model to a smaller "student" model. The key idea is to train the student model to mimic the teacher's outputs.The concept of KD was first popularized by the work of Geoffrey Hinton, Oriol Vinyals, and Jeff Dean in their paper ["Distilling the Knowledge in a Neural Network" (2015)](https://arxiv.org/abs/1503.02531).
+One popular technique is knowledge distillation (KD), which transfers knowledge from a large, complex "teacher" model to a smaller "student" model. The key idea is to train the student model to mimic the teacher's outputs. The concept of KD was first popularized by @hinton2015distilling.
##### Overview and Benefits
@@ -199,7 +199,7 @@ Another core concept is "temperature scaling" in the softmax function. It plays
These components, when adeptly configured and harmonized, enable the student model to assimilate the teacher model's knowledge, crafting a pathway towards efficient and robust smaller models that retain the predictive prowess of their larger counterparts.
-
+
##### Challenges
@@ -211,21 +211,21 @@ These challenges underscore the necessity for a thorough and nuanced approach to
#### Low-rank Matrix Factorization
-Similar in approximation theme, low-rank matrix factorization (LRFM) is a mathematical technique used in linear algebra and data analysis to approximate a given matrix by decomposing it into two or more lower-dimensional matrices. The fundamental idea is to express a high-dimensional matrix as a product of lower-rank matrices, which can help reduce the complexity of data while preserving its essential structure. Mathematically, given a matrix $A \in \mathbb{R}^{m \times n}$, LRMF seeks matrices $U \in \mathbb{R}^{m \times k}$ and $V \in \mathbb{R}^{k \times n}$ such that $A \approx UV$, where $k$ is the rank and is typically much smaller than $m$ and $n$.
+Similar in approximation theme, low-rank matrix factorization (LRMF) is a mathematical technique used in linear algebra and data analysis to approximate a given matrix by decomposing it into two or more lower-dimensional matrices. The fundamental idea is to express a high-dimensional matrix as a product of lower-rank matrices, which can help reduce the complexity of data while preserving its essential structure. Mathematically, given a matrix $A \in \mathbb{R}^{m \times n}$, LRMF seeks matrices $U \in \mathbb{R}^{m \times k}$ and $V \in \mathbb{R}^{k \times n}$ such that $A \approx UV$, where $k$ is the rank and is typically much smaller than $m$ and $n$.
##### Background and Benefits
-One of the seminal works in the realm of matrix factorization, particularly in the context of recommendation systems, is the paper by Yehuda Koren, Robert Bell, and Chris Volinsky, ["Matrix Factorization Techniques for Recommender Systems" (2009)]([https://ieeexplore.ieee.org/document/5197422](https://ieeexplore.ieee.org/document/5197422)). The authors delve into various factorization models, providing insights into their efficacy in capturing the underlying patterns in the data and enhancing predictive accuracy in collaborative filtering. LRFM has been widely applied in recommendation systems (such as Netflix, Facebook, etc.), where the user-item interaction matrix is factorized to capture latent factors corresponding to user preferences and item attributes.
+One of the seminal works in the realm of matrix factorization, particularly in the context of recommendation systems, is the paper by Yehuda Koren, Robert Bell, and Chris Volinsky, ["Matrix Factorization Techniques for Recommender Systems" (2009)]([https://ieeexplore.ieee.org/document/5197422](https://ieeexplore.ieee.org/document/5197422)). The authors delve into various factorization models, providing insights into their efficacy in capturing the underlying patterns in the data and enhancing predictive accuracy in collaborative filtering. LRMF has been widely applied in recommendation systems (such as Netflix, Facebook, etc.), where the user-item interaction matrix is factorized to capture latent factors corresponding to user preferences and item attributes.
The main advantage of low-rank matrix factorization lies in its ability to reduce data dimensionality as shown in the image below where there are fewer parameters to store, making it computationally more efficient and reducing storage requirements at the cost of some additional compute. This can lead to faster computations and more compact data representations, which is especially valuable when dealing with large datasets. Additionally, it may aid in noise reduction and can reveal underlying patterns and relationships in the data.
-
+
##### Challenges
But practitioners and researchers encounter a spectrum of challenges and considerations that necessitate careful attention and strategic approaches. As with any lossy compression technique, we may lose information during this approximation process: choosing the correct rank that balances the information lost and the computational costs is tricky as well and adds an additional hyper-parameter to tune for.
-Low-rank matrix factorization is a valuable tool for dimensionality reduction and making compute fit onto edge devices but, like other techniques, needs to be carefully tuned to the model and task at hand. A key challenge resides in managing the computational complexity inherent to LRMF, especially when grappling with high-dimensional and large-scale data. The computational burden, particularly in the context of real-time applications and massive datasets, remains a significant hurdle for effectively using LRFM.
+Low-rank matrix factorization is a valuable tool for dimensionality reduction and making compute fit onto edge devices but, like other techniques, needs to be carefully tuned to the model and task at hand. A key challenge resides in managing the computational complexity inherent to LRMF, especially when grappling with high-dimensional and large-scale data. The computational burden, particularly in the context of real-time applications and massive datasets, remains a significant hurdle for effectively using LRMF.
Moreover, the conundrum of choosing the optimal rank, \(k\), for the factorization introduces another layer of complexity. The selection of \(k\) inherently involves a trade-off between approximation accuracy and model simplicity, and identifying a rank that adeptly balances these conflicting objectives often demands a combination of domain expertise, empirical validation, and sometimes, heuristic approaches. The challenge is further amplified when the data encompasses noise or when the inherent low-rank structure is not pronounced, making the determination of a suitable \(k\) even more elusive.
@@ -237,13 +237,13 @@ Furthermore, in scenarios where data evolves or grows over time, developing LRMF
Similar to low-rank matrix factorization, more complex models may store weights in higher dimensions, such as tensors: tensor decomposition is the higher-dimensional analogue of matrix factorization, where a model tensor is decomposed into lower rank components, which again are easier to compute on and store but may suffer from the same issues as mentioned above of information loss and nuanced hyperparameter tuning. Mathematically, given a tensor $\mathcal{A}$, tensor decomposition seeks to represent $\mathcal{A}$ as a combination of simpler tensors, facilitating a compressed representation that approximates the original data while minimizing the loss of information.
-The work of Tamara G. Kolda and Brett W. Bader, ["Tensor Decompositions and Applications"](https://epubs.siam.org/doi/abs/10.1137/07070111X) (2009), stands out as a seminal paper in the field of tensor decompositions. The authors provide a comprehensive overview of various tensor decomposition methods, exploring their mathematical underpinnings, algorithms, and a wide array of applications, ranging from signal processing to data mining. Of course, the reason we are discussing it is because it has huge potential for system performance improvements, particularly in the space of TinyML, where throughput and memory footprint savings are crucial to feasibility of deployments .
+The work of Tamara G. Kolda and Brett W. Bader, ["Tensor Decompositions and Applications"](https://epubs.siam.org/doi/abs/10.1137/07070111X) (2009), stands out as a seminal paper in the field of tensor decompositions. The authors provide a comprehensive overview of various tensor decomposition methods, exploring their mathematical underpinnings, algorithms, and a wide array of applications, ranging from signal processing to data mining. Of course, the reason we are discussing it is because it has huge potential for system performance improvements, particularly in the space of TinyML, where throughput and memory footprint savings are crucial to feasibility of deployments.
-
+
### Edge-Aware Model Design
-Finally, we reach the other end of the gradient, where we specifically make model architecture decisions directly given knowledge of the edge devices we wish to deploy on.
+Finally, we reach the other end of the hardware-software gradient, where we specifically make model architecture decisions directly given knowledge of the edge devices we wish to deploy on.
As covered in previous sections, edge devices are constrained specifically with limitations on memory and parallelizable computations: as such, if there are critical inference speed requirements, computations must be flexible enough to satisfy hardware constraints, something that can be designed at the model architecture level. Furthermore, trying to cram SOTA large ML models onto edge devices even after pruning and compression is generally infeasible purely due to size: the model complexity itself must be chosen with more nuance as to more feasibly fit the device. Edge ML developers have approached this architectural challenge both through designing bespoke edge ML model architectures and through device-aware neural architecture search (NAS), which can more systematically generate feasible on-device model architectures.
@@ -251,17 +251,25 @@ As covered in previous sections, edge devices are constrained specifically with
One edge friendly architecture design is depthwise separable convolutions. Commonly used in deep learning for image processing, it consists of two distinct steps: the first is the depthwise convolution, where each input channel is convolved independently with its own set of learnable filters. This step reduces computational complexity by a significant margin compared to standard convolutions, as it drastically reduces the number of parameters and computations involved. The second step is the pointwise convolution, which combines the output of the depthwise convolution channels through a 1x1 convolution, creating inter-channel interactions. This approach offers several advantages. Pros include reduced model size, faster inference times, and often better generalization due to fewer parameters, making it suitable for mobile and embedded applications. However, depthwise separable convolutions may not capture complex spatial interactions as effectively as standard convolutions and might require more depth (layers) to achieve the same level of representational power, potentially leading to longer training times. Nonetheless, their efficiency in terms of parameters and computation makes them a popular choice in modern convolutional neural network architectures.
-
+
#### Example Model Architectures
-In this vein, a number of recent architectures have been, from inception, specifically designed for maximizing accuracy on an edge deployment, notably SqueezeNet, MobileNet, and EfficientNet. [SqueezeNet]([https://arxiv.org/abs/1602.07360](https://arxiv.org/abs/1602.07360)), for instance, utilizes a compact architecture with 1x1 convolutions and fire modules to minimize the number of parameters while maintaining strong accuracy. [MobileNet]([https://arxiv.org/abs/1704.04861](https://arxiv.org/abs/1704.04861)), on the other hand, employs the aforementioned depthwise separable convolutions to reduce both computation and model size. [EfficientNet]([https://arxiv.org/abs/1905.11946](https://arxiv.org/abs/1905.11946)) takes a different approach by optimizing network scaling (i.e. varying the depth, width and resolution of a network) and compound scaling, a more nuanced variation network scaling, to achieve superior performance with fewer parameters. These models are essential in the context of edge computing where limited processing power and memory require lightweight yet effective models that can efficiently perform tasks such as image recognition, object detection, and more. Their design principles showcase the importance of intentionally tailored model architecture for edge computing, where performance and efficiency must fit within constraints.
+In this vein, a number of recent architectures have been, from inception, specifically designed for maximizing accuracy on an edge deployment, notably SqueezeNet, MobileNet, and EfficientNet.
+
+* [SqueezeNet]([https://arxiv.org/abs/1602.07360](https://arxiv.org/abs/1602.07360)) by @iandola2016squeezenet for instance, utilizes a compact architecture with 1x1 convolutions and fire modules to minimize the number of parameters while maintaining strong accuracy.
+
+* [MobileNet]([https://arxiv.org/abs/1704.04861](https://arxiv.org/abs/1704.04861)) by @howard2017mobilenets, on the other hand, employs the aforementioned depthwise separable convolutions to reduce both computation and model size.
+
+* [EfficientNet]([https://arxiv.org/abs/1905.11946](https://arxiv.org/abs/1905.11946)) by @tan2020efficientnet takes a different approach by optimizing network scaling (i.e. varying the depth, width and resolution of a network) and compound scaling, a more nuanced variation network scaling, to achieve superior performance with fewer parameters.
+
+These models are essential in the context of edge computing where limited processing power and memory require lightweight yet effective models that can efficiently perform tasks such as image recognition, object detection, and more. Their design principles showcase the importance of intentionally tailored model architecture for edge computing, where performance and efficiency must fit within constraints.
#### Streamlining Model Architecture Search
-Finally, systematized pipelines for searching for performant edge-compatible model architectures are possible through frameworks like [TinyNAS](https://arxiv.org/abs/2007.10319) and [MorphNet]([https://arxiv.org/abs/1711.06798](https://arxiv.org/abs/1711.06798)).
+Finally, systematized pipelines for searching for performant edge-compatible model architectures are possible through frameworks like [TinyNAS](https://arxiv.org/abs/2007.10319) by @lin2020mcunet and [MorphNet]([https://arxiv.org/abs/1711.06798](https://arxiv.org/abs/1711.06798)) by @gordon2018morphnet.
-TinyNAS is an innovative neural architecture search framework introduced in the MCUNet paper, designed to efficiently discover lightweight neural network architectures for edge devices with limited computational resources. Leveraging reinforcement learning and a compact search space of micro neural modules, TinyNAS optimizes for both accuracy and latency, enabling the deployment of deep learning models on microcontrollers, IoT devices, and other resource-constrained platforms. Specifically, TinyNAS, in conjunction with a network optimizer TinyEngine, generates different search spaces by scaling the input resolution and the model width of a model, then collects the computation FLOPs distribution of satisfying networks within the search space to evaluate its priority. TinyNAS relies on the assumption that a search space that accommodates higher FLOPs under memory constraint can produce higher accuracy models, something that the authors verified in practice in their work. In empirical performance, TinyEngine reduced models the peak memory usage by around 3.4 times and accelerated inference by 1.7 to 3.3 times compared to [TFLite]([https://www.tensorflow.org/lite](https://www.tensorflow.org/lite)) and [CMSIS-NN]([https://www.keil.com/pack/doc/CMSIS/NN/html/index.html](https://www.keil.com/pack/doc/CMSIS/NN/html/index.html))..
+TinyNAS is an innovative neural architecture search framework introduced in the MCUNet paper, designed to efficiently discover lightweight neural network architectures for edge devices with limited computational resources. Leveraging reinforcement learning and a compact search space of micro neural modules, TinyNAS optimizes for both accuracy and latency, enabling the deployment of deep learning models on microcontrollers, IoT devices, and other resource-constrained platforms. Specifically, TinyNAS, in conjunction with a network optimizer TinyEngine, generates different search spaces by scaling the input resolution and the model width of a model, then collects the computation FLOPs distribution of satisfying networks within the search space to evaluate its priority. TinyNAS relies on the assumption that a search space that accommodates higher FLOPs under memory constraint can produce higher accuracy models, something that the authors verified in practice in their work. In empirical performance, TinyEngine reduced the peak memory usage of models by around 3.4 times and accelerated inference by 1.7 to 3.3 times compared to [TFLite]([https://www.tensorflow.org/lite](https://www.tensorflow.org/lite)) and [CMSIS-NN]([https://www.keil.com/pack/doc/CMSIS/NN/html/index.html](https://www.keil.com/pack/doc/CMSIS/NN/html/index.html))..
Similarly, MorphNet is a neural network optimization framework designed to automatically reshape and morph the architecture of deep neural networks, optimizing them for specific deployment requirements. It achieves this through two steps: first, it leverages a set of customizable network morphing operations, such as widening or deepening layers, to dynamically adjust the network's structure. These operations enable the network to adapt to various computational constraints, including model size, latency, and accuracy targets, which are extremely prevalent in edge computing usage. In the second step, MorphNet uses a reinforcement learning-based approach to search for the optimal permutation of morphing operations, effectively balancing the trade-off between model size and performance. This innovative method allows deep learning practitioners to automatically tailor neural network architectures to specific application and hardware requirements, ensuring efficient and effective deployment across various platforms.
@@ -272,13 +280,13 @@ TinyNAS and MorphNet represent a few of the many significant advancements in the
Numerics representation involves a myriad of considerations, including but not limited to, the precision of numbers, their encoding formats, and the arithmetic operations facilitated. It invariably involves a rich array of different trade-offs, where practitioners are tasked with navigating between numerical accuracy and computational efficiency. For instance, while lower-precision numerics may offer the allure of reduced memory usage and expedited computations, they concurrently present challenges pertaining to numerical stability and potential degradation of model accuracy.
-### Motivation
+#### Motivation
The imperative for efficient numerics representation arises, particularly as efficient model optimization alone falls short when adapting models for deployment on low-powered edge devices operating under stringent constraints.
Beyond minimizing memory demands, the tremendous potential of efficient numerics representation lies in but is not limited to these fundamental ways. By diminishing computational intensity, efficient numerics can thereby amplify computational speed, allowing more complex models to compute on low-powered devices. Reducing the bit precision of weights and activations on heavily over-parameterized models enables condensation of model size for edge devices without significantly harming the model's predictive accuracy. With the omnipresence of neural networks in models, efficient numerics has a unique advantage in leveraging the layered structure of NNs to vary numeric precision across layers, minimizing precision in resistant layers while preserving higher precision in sensitive layers.
-In this segment, we'll delve into how practitioners can harness the principles of hardware-software co-design at the lowest levels of a model to facilitate compatibility with edge devices. Kicking off with an introduction to the numerics, we will examine its implications for device memory and computational complexity. Subsequently, we will embark on a discussion regarding the trade-offs entailed in adopting this strategy, followed by a deep dive into a paramount method of efficient numerics: quantization.
+In this section, we will dive into how practitioners can harness the principles of hardware-software co-design at the lowest levels of a model to facilitate compatibility with edge devices. Kicking off with an introduction to the numerics, we will examine its implications for device memory and computational complexity. Subsequently, we will embark on a discussion regarding the trade-offs entailed in adopting this strategy, followed by a deep dive into a paramount method of efficient numerics: quantization.
### The Basics
@@ -286,7 +294,7 @@ In this segment, we'll delve into how practitioners can harness the principles o
Numerical data, the bedrock upon which machine learning models stand, manifest in two primary forms. These are integers and floating point numbers.
-**Integers** : Whole numbers, devoid of fractional components, integers (e.g., -3, 0, 42) are key in scenarios demanding discrete values. For instance, in ML, class labels in a classification task might be represented as integers, where "cat", "dog", and "bird" could be encoded as 0, 1, and 2 respectively.
+**Integers:** Whole numbers, devoid of fractional components, integers (e.g., -3, 0, 42) are key in scenarios demanding discrete values. For instance, in ML, class labels in a classification task might be represented as integers, where "cat", "dog", and "bird" could be encoded as 0, 1, and 2 respectively.
**Floating-Point Numbers:** Encompassing real numbers, floating-point numbers (e.g., -3.14, 0.01, 2.71828) afford the representation of values with fractional components. In ML model parameters, weights might be initialized with small floating-point values, such as 0.001 or -0.045, to commence the training process. Currently, there are 4 popular precision formats discussed below.
@@ -304,25 +312,19 @@ Precision, delineating the exactness with which a number is represented, bifurca
**Bfloat16:** Brain Floating-Point Format or Bfloat16, also employs 16 bits but allocates them differently compared to FP16: 1 bit for the sign, 8 bits for the exponent, and 7 bits for the fraction. This format, developed by Google, prioritizes a larger exponent range over precision, making it particularly useful in deep learning applications where the dynamic range is crucial.
-](https://storage.googleapis.com/gweb-cloudblog-publish/images/Three_floating-point_formats.max-624x261.png)
+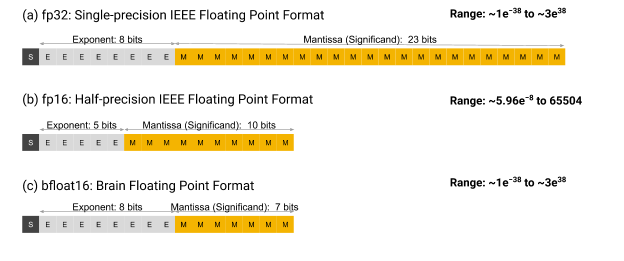
**Integer:** Integer representations are made using 8, 4, and 2 bits. They are often used during the inference phase of neural networks, where the weights and activations of the model are quantized to these lower precisions. Integer representations are deterministic and offer significant speed and memory advantages over floating-point representations. For many inference tasks, especially on edge devices, the slight loss in accuracy due to quantization is often acceptable given the efficiency gains. An extreme form of integer numerics is for binary neural networks (BNNs), where weights and activations are constrained to one of two values: either +1 or -1.
-| Precision | Pros | Cons |
-
-|------------|-----------------------------------------------------------|--------------------------------------------------|
-
-| **FP32** (Floating Point 32-bit) | - Standard precision used in most deep learning frameworks.\ - High accuracy due to ample representational capacity.\ - Well-suited for training. | - High memory usage.\ - Slower inference times compared to quantized models.\ - Higher energy consumption. |
-
-| **FP16** (Floating Point 16-bit) | - Reduces memory usage compared to FP32.\ - Speeds up computations on hardware that supports FP16.\ - Often used in mixed-precision training to balance speed and accuracy. | - Lower representational capacity compared to FP32.\ - Risk of numerical instability in some models or layers. |
-
-| **INT8** (8-bit Integer) | - Significantly reduced memory footprint compared to floating-point representations.\ - Faster inference if hardware supports INT8 computations.\ - Suitable for many post-training quantization scenarios. | - Quantization can lead to some accuracy loss.\ - Requires careful calibration during quantization to minimize accuracy degradation. |
+| **Precision** | **Pros** | **Cons** |
+|---------------------------------------|------------------------------------------------------------------------------------------------------|----------------------------------------------------------------------------------------------------------------------------|
+| **FP32** (Floating Point 32-bit) | • Standard precision used in most deep learning frameworks.
• High accuracy due to ample representational capacity.
• Well-suited for training. | • High memory usage.
• Slower inference times compared to quantized models.
• Higher energy consumption. |
+| **FP16** (Floating Point 16-bit) | • Reduces memory usage compared to FP32.
• Speeds up computations on hardware that supports FP16.
• Often used in mixed-precision training to balance speed and accuracy. | • Lower representational capacity compared to FP32.
• Risk of numerical instability in some models or layers. |
+| **INT8** (8-bit Integer) | • Significantly reduced memory footprint compared to floating-point representations.
• Faster inference if hardware supports INT8 computations.
• Suitable for many post-training quantization scenarios. | • Quantization can lead to some accuracy loss.
• Requires careful calibration during quantization to minimize accuracy degradation. |
+| **INT4** (4-bit Integer) | • Even lower memory usage than INT8.
• Further speed-up potential for inference. | • Higher risk of accuracy loss compared to INT8.
• Calibration during quantization becomes more critical. |
+| **Binary** | • Minimal memory footprint (only 1 bit per parameter).
• Extremely fast inference due to bitwise operations.
• Power efficient. | • Significant accuracy drop for many tasks.
• Complex training dynamics due to extreme quantization. |
+| **Ternary** | • Low memory usage but slightly more than binary.
• Offers a middle ground between representation and efficiency. | • Accuracy might still be lower than higher precision models.
• Training dynamics can be complex. |
-| **INT4** (4-bit Integer) | - Even lower memory usage than INT8.\ - Further speed-up potential for inference. | - Higher risk of accuracy loss compared to INT8.\ - Calibration during quantization becomes more critical. |
-
-| **Binary** | - Minimal memory footprint (only 1 bit per parameter).\ - Extremely fast inference due to bitwise operations.\ - Power efficient. | - Significant accuracy drop for many tasks.\ - Complex training dynamics due to extreme quantization. |
-
-| **Ternary** | - Low memory usage but slightly more than binary.\ - Offers a middle ground between representation and efficiency. | - Accuracy might still be lower than higher precision models.\ - Training dynamics can be complex. |
#### Numeric Encoding and Storage
@@ -371,17 +373,18 @@ Numerical precision directly impacts computational complexity, influencing the t
In addition to pure runtimes, there is also a concern over energy efficiency. Not all numerical computations are created equal from the underlying hardware standpoint. Some numerical operations are more energy efficient than others. For example, the figure below shows that integer addition is much more energy efficient than integer multiplication.
-
-
-Source: [https://ieeexplore.ieee.org/document/6757323](https://ieeexplore.ieee.org/document/6757323)
-
+
+
+
+
+
#### Hardware Compatibility
Ensuring compatibility and optimized performance across diverse hardware platforms is another challenge in numerics representation. Different hardware, such as CPUs, GPUs, TPUs, and FPGAs, have varying capabilities and optimizations for handling different numeric precisions. For example, certain GPUs might be optimized for Float32 computations, while others might provide accelerations for Float16. Developing and optimizing ML models that can leverage the specific numerical capabilities of different hardware, while ensuring that the model maintains its accuracy and robustness, requires careful consideration and potentially additional development and testing efforts.
-Precision and Accuracy Trade-offs
+#### Precision and Accuracy Trade-offs
The trade-off between numerical precision and model accuracy is a nuanced challenge in numerics representation. Utilizing lower-precision numerics, such as Float16, might conserve memory and expedite computations but can also introduce issues like quantization error and reduced numerical range. For instance, training a model with Float16 might introduce challenges in representing very small gradient values, potentially impacting the convergence and stability of the training process. Furthermore, in certain applications, such as scientific simulations or financial computations, where high precision is paramount, the use of lower-precision numerics might not be permissible due to the risk of accruing significant errors.
@@ -428,13 +431,13 @@ These examples illustrate diverse scenarios where the challenges of numerics rep
### Quantization {#sec-quant}
-Quantization is prevalent in various scientific and technological domains, essentially involves the **mapping or constraining of a continuous set or range into a discrete counterpart to minimize the number of bits required**.
+Quantization is prevalent in various scientific and technological domains, and it essentially involves the **mapping or constraining of a continuous set or range into a discrete counterpart to minimize the number of bits required**.
#### History
Historically, the idea of quantization is not novel and can be traced back to ancient times, particularly in the realm of music and astronomy. In music, the Greeks utilized a system of tetrachords, segmenting the continuous range of pitches into discrete notes, thereby quantizing musical sounds. In astronomy and physics, the concept of quantization was present in the discretized models of planetary orbits, as seen in the Ptolemaic and Copernican systems.
-During the 1800s, quantization-based discretization was used to approximate the calculation of integrals, and further used to investigate the impact of rounding errors on the integration result. However, the term "quantization" was firmly embedded in scientific literature with the advent of quantum mechanics in the early 20th century, where it was used to describe the phenomenon that certain physical properties, such as energy, exist only in discrete, quantized states. This principle was pivotal in explaining phenomena at the atomic and subatomic levels. In the digital age, quantization found its application in signal processing, where continuous signals are converted into a discrete digital form, and in numerical algorithms, where computations on real-valued numbers are performed with finite-precision arithmetic.
+During the 1800s, quantization-based discretization was used to approximate the calculation of integrals, and further used to investigate the impact of rounding errors on the integration result. With algorithms, Lloyd's K-Means Algorithm is a classic example of quantization. However, the term "quantization" was firmly embedded in scientific literature with the advent of quantum mechanics in the early 20th century, where it was used to describe the phenomenon that certain physical properties, such as energy, exist only in discrete, quantized states. This principle was pivotal in explaining phenomena at the atomic and subatomic levels. In the digital age, quantization found its application in signal processing, where continuous signals are converted into a discrete digital form, and in numerical algorithms, where computations on real-valued numbers are performed with finite-precision arithmetic.
Extending upon this second application and relevant to this section, it is used in computer science to optimize neural networks by reducing the precision of the network weights. Thus, quantization, as a concept, has been subtly woven into the tapestry of scientific and technological development, evolving and adapting to the needs and discoveries of various epochs.
@@ -446,15 +449,13 @@ In signal processing, the continuous sine wave can be quantized into discrete va

-In the quantized version shown below, the continuous sine wave is sampled at regular intervals (in this case, every \(\frac{\pi}{4}\) radians), and only these sampled values are represented in the digital version of the signal. The step-wise lines between the points show one way to represent the quantized signal in a piecewise-constant form. This is a simplified example of how analog-to-digital conversion works, where a continuous signal is mapped to a discrete set of values, enabling it to be represented and processed digitally.
+In the quantized version shown below, the continuous sine wave is sampled at regular intervals (in this case, every $\frac{\pi}{4}$ radians), and only these sampled values are represented in the digital version of the signal. The step-wise lines between the points show one way to represent the quantized signal in a piecewise-constant form. This is a simplified example of how analog-to-digital conversion works, where a continuous signal is mapped to a discrete set of values, enabling it to be represented and processed digitally.

-Returning to the context of Machine Learning (ML), quantization refers to the process of constraining the possible values that numerical parameters (such as weights and biases) can take to a discrete set, thereby reducing the precision of the parameters and consequently, the model's memory footprint. When properly implemented, quantization can reduce model size by up to 4x and improve inference latency and throughput by up to 2-3x. For example, an Image Classification model like ResNet-50 can be compressed from 96MB down to 24MB with 8-bit quantization.There is typically less than 1% loss in model accuracy from well tuned quantization. Accuracy can often be recovered by re-training the quantized model with quantization aware training techniques. Therefore, this technique has emerged to be very important in deploying ML models to resource-constrained environments, such as mobile devices, IoT devices, and edge computing platforms, where computational resources (memory and processing power) are limited.
-
-
+Returning to the context of Machine Learning (ML), quantization refers to the process of constraining the possible values that numerical parameters (such as weights and biases) can take to a discrete set, thereby reducing the precision of the parameters and consequently, the model's memory footprint. When properly implemented, quantization can reduce model size by up to 4x and improve inference latency and throughput by up to 2-3x. For example, an Image Classification model like ResNet-50 can be compressed from 96MB down to 24MB with 8-bit quantization. There is typically less than 1% loss in model accuracy from well tuned quantization. Accuracy can often be recovered by re-training the quantized model with quantization aware training techniques. Therefore, this technique has emerged to be very important in deploying ML models to resource-constrained environments, such as mobile devices, IoT devices, and edge computing platforms, where computational resources (memory and processing power) are limited.
-[Quantization figure - Example figure showing reduced model size from quantization]()
+
There are several dimensions to quantization such as uniformity, stochasticity (or determinism), symmetry, granularity (across layers/channels/groups or even within channels), range calibration considerations (static vs dynamic), and fine-tuning methods (QAT, PTQ, ZSQ). We examine these below.
@@ -466,29 +467,33 @@ Uniform quantization involves mapping continuous or high-precision values to a l
The process for implementing uniform quantization starts with choosing a range of real numbers to be quantized. The next step is to select a quantization function and map the real values to the integers representable by the bit-width of the quantized representation. For instance, a popular choice for a quantization function is:
+$$
Q(r)=Int(r/S) - Z
+$$
where Q is the quantization operator, r is a real valued input (in our case, an activation or weight), S is a real valued scaling factor, and Z is an integer zero point. The Int function maps a real value to an integer value through a rounding operation. Through this function, we have effectively mapped real values r to some integer values, resulting in quantized levels which are uniformly spaced.
When the need arises for practitioners to retrieve the original higher precision values, real values r can be recovered from quantized values through an operation known as **dequantization**. In the example above, this would mean performing the following operation on our quantized value:
-r ̃ = S(Q(r) + Z) (~ should be on top, ignore)
+$$
+\bar{r} = S(Q(r) + Z)
+$$
-As discussed, some precision in the real value is lost by quantization. In this case, the recovered value r ̃ will not exactly match r due to the rounding operation. This is an important tradeoff to note; however, in many successful uses of quantization, the loss of precision can be negligible and the test accuracy remains high. Despite this, uniform quantization continues to be the current de-facto choice due to its simplicity and efficient mapping to hardware.
+As discussed, some precision in the real value is lost by quantization. In this case, the recovered value $\bar{r}$ will not exactly match r due to the rounding operation. This is an important tradeoff to note; however, in many successful uses of quantization, the loss of precision can be negligible and the test accuracy remains high. Despite this, uniform quantization continues to be the current de-facto choice due to its simplicity and efficient mapping to hardware.
#### Non-uniform Quantization
Non-uniform quantization, on the other hand, does not maintain a consistent interval between quantized values. This approach might be used to allocate more possible discrete values in regions where the parameter values are more densely populated, thereby preserving more detail where it is most needed. For instance, in bell-shaped distributions of weights with long tails, a set of weights in a model predominantly lies within a certain range; thus, more quantization levels might be allocated to that range to preserve finer details, enabling us to better capture information. However, one major weakness of non-uniform quantization is that it requires dequantization before higher precision computations due to its non-uniformity, restricting its ability to accelerate computation compared to uniform quantization.
-Typically, a rule-based non-uniform quantization uses a logarithmic distribution of exponentially increasing steps and levels as opposed to linearly. Another popular branch lies in binary-code-based quantization where real number vectors are quantized into binary vectors with a scaling factor. Notably, there is no closed form solution for minimizing errors between the real value and non-uniformly quantized value, so most quantizations in this field rely on heuristic solutions. For instance, recent work formulates non-uniform quantization as an optimization problem where the quantization steps/levels in quantizer Q are adjusted to minimize the difference between the original tensor and quantized counterpart.
+Typically, a rule-based non-uniform quantization uses a logarithmic distribution of exponentially increasing steps and levels as opposed to linearly. Another popular branch lies in binary-code-based quantization where real number vectors are quantized into binary vectors with a scaling factor. Notably, there is no closed form solution for minimizing errors between the real value and non-uniformly quantized value, so most quantizations in this field rely on heuristic solutions. For instance, [recent work](https://arxiv.org/abs/1802.00150) by @xu2018alternating formulates non-uniform quantization as an optimization problem where the quantization steps/levels in quantizer Q are adjusted to minimize the difference between the original tensor and quantized counterpart.
-\min\_Q ||Q(r)-r||^2
+$$
+\min_Q ||Q(r)-r||^2
+$$
Furthermore, learnable quantizers can be jointly trained with model parameters, and the quantization steps/levels are generally trained with iterative optimization or gradient descent. Additionally, clustering has been used to alleviate information loss from quantization. While capable of capturing higher levels of detail, non-uniform quantization schemes can be difficult to deploy efficiently on general computation hardware, making it less-preferred to methods which use uniform quantization.
-
-
-_Comparison between uniform quantization (left) and non-uniform quantization (right) (Credit: __**A Survey of Quantization Methods for Efficient Neural Network Inference**__ )._
+
#### Stochastic Quantization
@@ -504,7 +509,7 @@ Zero-shot quantization refers to the process of converting a full-precision deep
### Calibration
-Calibration is the process of selecting the most effective clipping range [\alpha, \beta] for weights and activations to be quantized to. For example, consider quantizing activations that originally have a floating-point range between -6 and 6 to 8-bit integers. If you just take the minimum and maximum possible 8-bit integer values (-128 to 127) as your quantization range, it might not be the most effective. Instead, calibration would involve passing a representative dataset then use this observed range for quantization.
+Calibration is the process of selecting the most effective clipping range [$\alpha$, $\beta$] for weights and activations to be quantized to. For example, consider quantizing activations that originally have a floating-point range between -6 and 6 to 8-bit integers. If you just take the minimum and maximum possible 8-bit integer values (-128 to 127) as your quantization range, it might not be the most effective. Instead, calibration would involve passing a representative dataset then use this observed range for quantization.
There are many calibration methods but a few commonly used include:
@@ -514,41 +519,36 @@ Entropy: Use KL divergence to minimize information loss between the original flo
Percentile: Set the range to a percentile of the distribution of absolute values seen during calibration. For example, 99% calibration would clip 1% of the largest magnitude values.
-
-
-Src: Integer quantization for deep learning inference
+
Importantly, the quality of calibration can make a difference between a quantized model that retains most of its accuracy and one that degrades significantly. Hence, it's an essential step in the quantization process. When choosing a calibration range, there are two types: symmetric and asymmetric.
#### Symmetric Quantization
-Symmetric quantization maps real values to a symmetrical clipping range centered around 0. This involves choosing a range [\alpha, \beta] where \alpha = -\beta. For example, one symmetrical range would be based on the min/max values of the real values such that: -\alpha = \beta = max(abs(r\_max), abs(r\_min)).
+Symmetric quantization maps real values to a symmetrical clipping range centered around 0. This involves choosing a range [$\alpha$, $\beta$] where $\alpha = -\beta$. For example, one symmetrical range would be based on the min/max values of the real values such that: -$\alpha = \beta = max(abs(r_{max}), abs(r_{min}))$.
-Symmetric clipping ranges are the most widely adopted in practice as they have the advantage of easier implementation. In particular, the zeroing out of the zero point can lead to reduction in computational cost during inference ["Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation" (2023)]([https://arxiv.org/abs/2004.09602](https://arxiv.org/abs/2004.09602)) .
+Symmetric clipping ranges are the most widely adopted in practice as they have the advantage of easier implementation. In particular, the mapping of zero to zero in the clipping range (sometimes called "zeroing out of the zero point") can lead to reduction in computational cost during inference [(@intquantfordeepinf)](https://arxiv.org/abs/2004.09602) .
#### Asymmetric Quantization
-Asymmetric quantization maps real values to an asymmetrical clipping range that isn't necessarily centered around 0. It involves choosing a range [\alpha, \beta] where \alpha \neq -\beta. For example, selecting a range based on the minimum and maximum real values, or where \alpha = r\_min and \beta = r\_max, creates an asymmetric range. Typically, asymmetric quantization produces tighter clipping ranges compared to symmetric quantization, which is important when target weights and activations are imbalanced, e.g., the activation after the ReLU always has non-negative values. Despite producing tighter clipping ranges, asymmetric quantization is less preferred to symmetric quantization as it doesn't always zero out the real value zero.
-
-
+Asymmetric quantization maps real values to an asymmetrical clipping range that isn't necessarily centered around 0. It involves choosing a range [$\alpha$, $\beta$] where $\alpha \neq -\beta$. For example, selecting a range based on the minimum and maximum real values, or where $\alpha = r_{min}$ and $\beta = r_{max}$, creates an asymmetric range. Typically, asymmetric quantization produces tighter clipping ranges compared to symmetric quantization, which is important when target weights and activations are imbalanced, e.g., the activation after the ReLU always has non-negative values. Despite producing tighter clipping ranges, asymmetric quantization is less preferred to symmetric quantization as it doesn't always zero out the real value zero.
-_Illustration of symmetric quantization (left) and asymmetric quantization (right). Symmetric quantization maps real values to [-127, 127], and asymmetric maps to [-128, 127]. (Credit: __**A Survey of Quantization Methods for Efficient Neural Network Inference**__ )._
+![Illustration of symmetric quantization (left) and asymmetric quantization (right). Symmetric quantization maps real values to [-127, 127], and asymmetric maps to [-128, 127] (@surveyofquant).](images/efficientnumerics_symmetry.png)
-### Granularity
+#### Granularity
Upon deciding the type of clipping range, it is essential to tighten the range to allow a model to retain as much of its accuracy as possible. We'll be taking a look at convolutional neural networks as our way of exploring methods that fine tune the granularity of clipping ranges for quantization. The input activation of a layer in our CNN undergoes convolution with multiple convolutional filters. Every convolutional filter can possess a unique range of values. Consequently, one distinguishing feature of quantization approaches is the precision with which the clipping range [α,β] is determined for the weights.
-
-_Illustration of the main forms of quantization granularities. In layerwise quantization, the same clipping range is applied to all filters which belong to the same layer. Notice how this can result in lower quantization resolutions for channels with narrow distributions, e.g. Filter 1, Filter 2, and Filter C. A higher quantization resolution can be achieved using channelwise quantization which dedicates different clipping ranges to different channels. (Credit: __**A Survey of Quantization Methods for Efficient Neural Network Inference**__ )._
+
-1. Layerwise Quantization: This approach determines the clipping range by considering all of the weights in the convolutional filters of a layer. Then, the same clipping range is used for all convolutional filters. It's the simplest to implement, and, as such, it often results in sub-optimal accuracy due the wide variety of differing ranges between filters. For example, a convolutional kernel with a narrower range of parameters loses its quantization resolution due to another kernel in the same layer having a wider range. .
+1. Layerwise Quantization: This approach determines the clipping range by considering all of the weights in the convolutional filters of a layer. Then, the same clipping range is used for all convolutional filters. It's the simplest to implement, and, as such, it often results in sub-optimal accuracy due the wide variety of differing ranges between filters. For example, a convolutional kernel with a narrower range of parameters loses its quantization resolution due to another kernel in the same layer having a wider range.
2. Groupwise Quantization: This approach groups different channels inside a layer to calculate the clipping range. This method can be helpful when the distribution of parameters across a single convolution/activation varies a lot. In practice, this method was useful in Q-BERT [Q-BERT: Hessian based ultra low precision quantization of bert] for quantizing Transformer [Attention Is All You Need] models that consist of fully-connected attention layers. The downside with this approach comes with the extra cost of accounting for different scaling factors.
3. Channelwise Quantization: This popular method uses a fixed range for each convolutional filter that is independent of other channels. Because each channel is assigned a dedicated scaling factor, this method ensures a higher quantization resolution and often results in higher accuracy.
4. Sub-channelwise Quantization: Taking channelwise quantization to the extreme, this method determines the clipping range with respect to any groups of parameters in a convolution or fully-connected layer. It may result in considerable overhead since different scaling factors need to be taken into account when processing a single convolution or fully-connected layer.
Of these, channelwise quantization is the current standard used for quantizing convolutional kernels, since it enables the adjustment of clipping ranges for each individual kernel with negligible overhead.
-### Static and Dynamic Quantization
+#### Static and Dynamic Quantization
After determining the type and granularity of the clipping range, practitioners must decide when ranges are determined in their range calibration algorithms. There are two approaches to quantizing activations: static quantization and dynamic quantization.
@@ -562,92 +562,76 @@ Between the two, calculating the range dynamically usually is very costly, so mo
The two prevailing techniques for quantizing models are Post Training Quantization and Quantization Aware Training.
-**Post Training Quantization** - Post-training quantization (PTQ) is a quantization technique where the model is quantized after it has been trained.The model is trained in floating point and then weights and activations are quantized as a post-processing step. This is the simplest approach and does not require access to the training data. Unlike Quantization-Aware Training (QAT), PTQ sets weight and activation quantization parameters directly, making it low-overhead and suitable for limited or unlabeled data situations. However, not readjusting the weights after quantizing, especially in low-precision quantization can lead to very different behavior and thus lower accuracy. To tackle this, techniques like bias correction, equalizing weight ranges, and adaptive rounding methods have been developed. PTQ can also be applied in zero-shot scenarios, where no training or testing data are available. This method has been made even more efficient to benefit compute- and memory- intensive large language models. Recently, SmoothQuant, a training-free, accuracy-preserving, and general-purpose PTQ solution which enables 8-bit weight, 8-bit activation quantization for LLMs, has been developed, demonstrating up to 1.56x speedup and 2x memory reduction for LLMs with negligible loss in accuracy [SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models](2023)(https://arxiv.org/abs/2211.10438).
-
-
-
-
-_In PTQ, a pretrained model is calibrated using calibration data (e.g., a small subset of training data) to compute the clipping ranges and scaling factors. (Credit: __**A Survey of Quantization Methods for Efficient Neural Network Inference**__ )_
+**Post Training Quantization** - Post-training quantization (PTQ) is a quantization technique where the model is quantized after it has been trained. The model is trained in floating point and then weights and activations are quantized as a post-processing step. This is the simplest approach and does not require access to the training data. Unlike Quantization-Aware Training (QAT), PTQ sets weight and activation quantization parameters directly, making it low-overhead and suitable for limited or unlabeled data situations. However, not readjusting the weights after quantizing, especially in low-precision quantization can lead to very different behavior and thus lower accuracy. To tackle this, techniques like bias correction, equalizing weight ranges, and adaptive rounding methods have been developed. PTQ can also be applied in zero-shot scenarios, where no training or testing data are available. This method has been made even more efficient to benefit compute- and memory- intensive large language models. Recently, SmoothQuant, a training-free, accuracy-preserving, and general-purpose PTQ solution which enables 8-bit weight, 8-bit activation quantization for LLMs, has been developed, demonstrating up to 1.56x speedup and 2x memory reduction for LLMs with negligible loss in accuracy [(@smoothquant)](https://arxiv.org/abs/2211.10438).
-**Quantization Aware Training** - Quantization-aware training (QAT) is a fine-tuning of the PTQ model. The model is trained aware of quantization, allowing it to adjust for quantization effects. This produces better accuracy with quantized inference. Quantizing a trained neural network model with methods such as PTQ introduces perturbations that can deviate the model from its original convergence point. For instance, Krishnamoorthi showed that even with per-channel quantization, networks like MobileNet do not reach baseline accuracy with int8 Post Training Quantization (PTQ) and require Quantization Aware Training (QAT) [Quantizing deep convolutional networks for efficient inference](2018)([https://arxiv.org/abs/1806.08342](https://arxiv.org/abs/1806.08342)).To address this, QAT retrains the model with quantized parameters, employing forward and backward passes in floating point but quantizing parameters after each gradient update. Handling the non-differentiable quantization operator is crucial; a widely used method is the Straight Through Estimator (STE), approximating the rounding operation as an identity function. While other methods and variations exist, STE remains the most commonly used due to its practical effectiveness.
+
-
+
-_In QAT, a pretrained model is quantized and then finetuned using training data to adjust parameters and recover accuracy degradation. Note: the calibration process is often conducted in parallel with the finetuning process for QAT. (Credit: __**A Survey of Quantization Methods for Efficient Neural Network Inference**__ )._
+**Quantization Aware Training** - Quantization-aware training (QAT) is a fine-tuning of the PTQ model. The model is trained aware of quantization, allowing it to adjust for quantization effects. This produces better accuracy with quantized inference. Quantizing a trained neural network model with methods such as PTQ introduces perturbations that can deviate the model from its original convergence point. For instance, Krishnamoorthi showed that even with per-channel quantization, networks like MobileNet do not reach baseline accuracy with int8 Post Training Quantization (PTQ) and require Quantization Aware Training (QAT) [(@quantdeep)](https://arxiv.org/abs/1806.08342).To address this, QAT retrains the model with quantized parameters, employing forward and backward passes in floating point but quantizing parameters after each gradient update. Handling the non-differentiable quantization operator is crucial; a widely used method is the Straight Through Estimator (STE), approximating the rounding operation as an identity function. While other methods and variations exist, STE remains the most commonly used due to its practical effectiveness.
-Src: Integer quantization for deep learning inference 
+
-_Note that QAT is an extension of PTQ. It receives the model quantized by PTQ and retrains it to finetune quantized parameters._ Src: https://deci.ai/quantization-and-quantization-aware-training/
+
-
-
-Src: integer quantization for deep learning Inference: principles and empirical evaluations
+
| **Feature/Technique** | **Post Training Quantization** | **Quantization Aware Training** | **Dynamic Quantization** |
|------------------------------|------------------------------|------------------------------|------------------------------|
| **Pros** | | | |
-| **Simplicity** | ✓ | ✗ | ✗ |
-| **Accuracy Preservation** | ✗ | ✓ | ✓ |
-| **Adaptability** | ✗ | ✗ | ✓ |
-| **Optimized Performance** | ✗ | ✓ | Potentially |
+| Simplicity | ✓ | ✗ | ✗ |
+| Accuracy Preservation | ✗ | ✓ | ✓ |
+| Adaptability | ✗ | ✗ | ✓ |
+| Optimized Performance | ✗ | ✓ | Potentially |
| **Cons** | | | |
-| **Accuracy Degradation**| ✓ | ✗ | Potentially |
-| **Computational Overhead** | ✗ | ✓ | ✓ |
-| **Implementation Complexity** | ✗ | ✓ | ✓ |
+| Accuracy Degradation| ✓ | ✗ | Potentially |
+| Computational Overhead | ✗ | ✓ | ✓ |
+| Implementation Complexity | ✗ | ✓ | ✓ |
| **Tradeoffs** | | | |
-| **Speed vs. Accuracy** |✓ | ✗ | ✗ |
-| **Accuracy vs. Cost** | ✗ | ✓ | ✗ |
-| **Adaptability vs. Overhead** | ✗ | ✗ | ✓ |
+| Speed vs. Accuracy |✓ | ✗ | ✗ |
+| Accuracy vs. Cost | ✗ | ✓ | ✗ |
+| Adaptability vs. Overhead | ✗ | ✗ | ✓ |
### Weights vs. Activations
Weight Quantization: Involves converting the continuous or high-precision weights of a model to lower-precision, such as converting Float32 weights to quantized INT8 (integer) weights. This reduces the model size, thereby reducing the memory required to store the model and the computational resources needed to perform inference. For example, consider a weight matrix in a neural network layer with Float32 weights as [0.215, -1.432, 0.902, ...]. Through weight quantization, these might be mapped to INT8 values like [27, -183, 115, ...], significantly reducing the memory required to store them.
-[Figure X.2 - Diagram of quantizing weights and activations] 
+
-Activation Quantization: Involves quantizing the activation values (outputs of layers) during model inference. This can reduce the computational resources required during inference, but it introduces additional challenges in maintaining model accuracy due to the reduced precision of intermediate computations. For example, in a convolutional neural network (CNN), the activation maps (feature maps) produced by convolutional layers, originally in Float32, might be quantized to INT8 during inference to accelerate computation, especially on hardware optimized for integer arithmetic. Additionally, recent work has explored the use of Activation-aware Weight Quantization for LLM compression and acceleration, which involves protecting only 1% of the most important salient weights by observing the activations not weights [AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration](2023)(https://arxiv.org/pdf/2306.00978.pdf).
+Activation Quantization: Involves quantizing the activation values (outputs of layers) during model inference. This can reduce the computational resources required during inference, but it introduces additional challenges in maintaining model accuracy due to the reduced precision of intermediate computations. For example, in a convolutional neural network (CNN), the activation maps (feature maps) produced by convolutional layers, originally in Float32, might be quantized to INT8 during inference to accelerate computation, especially on hardware optimized for integer arithmetic. Additionally, recent work has explored the use of Activation-aware Weight Quantization for LLM compression and acceleration, which involves protecting only 1% of the most important salient weights by observing the activations not weights [(@awq)](https://arxiv.org/pdf/2306.00978.pdf).
### Trade-offs
Quantization invariably introduces a trade-off between model size/performance and accuracy. While it significantly reduces the memory footprint and can accelerate inference, especially on hardware optimized for low-precision arithmetic, the reduced precision can degrade model accuracy.
Model Size: A model with weights represented as Float32 being quantized to INT8 can theoretically reduce the model size by a factor of 4, enabling it to be deployed on devices with limited memory.
-
-Src: https://arxiv.org/abs/2211.10438
+
Inference Speed: Quantization can also accelerate inference, as lower-precision arithmetic is computationally less expensive. For example, certain hardware accelerators, like Google's Edge TPU, are optimized for INT8 arithmetic and can perform inference significantly faster with INT8 quantized models compared to their floating-point counterparts.
-
-
-Src: Integer quantization for deep learning inference
-
-Accuracy: The reduction in numerical precision post-quantization can lead to a degradation in model accuracy, which might be acceptable in certain applications (e.g., image classification) but not in others (e.g., medical diagnosis). Therefore, post-quantization, the model typically requires re-calibration or fine-tuning to mitigate accuracy loss. Furthermore, recent work has explored the use of Activation-aware Weight Quantization which is based on the observation that protecting only 1% of salient weights can greatly reduce quantization error [AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration](2023)(https://arxiv.org/pdf/2306.00978.pdf).
+
-
+Accuracy: The reduction in numerical precision post-quantization can lead to a degradation in model accuracy, which might be acceptable in certain applications (e.g., image classification) but not in others (e.g., medical diagnosis). Therefore, post-quantization, the model typically requires re-calibration or fine-tuning to mitigate accuracy loss. Furthermore, recent work has explored the use of [Activation-aware Weight Quantization (@awq)](https://arxiv.org/pdf/2306.00978.pdf) which is based on the observation that protecting only 1% of salient weights can greatly reduce quantization error.
-Src: [https://arxiv.org/abs/1510.00149](https://arxiv.org/abs/1510.00149)
-
-[Figure]()
+
### Quantization and Pruning
Pruning and quantization work well together, and it's been found that pruning doesn't hinder quantization. In fact, pruning can help reduce quantization error. Intuitively, this is due to pruning reducing the number of weights to quantize, thereby reducing the accumulated error from quantization. For example, an unpruned AlexNet has 60 million weights to quantize whereas a pruned AlexNet only has 6.7 million weights to quantize. This significant drop in weights helps reduce the error between quantizing the unpruned AlexNet vs. the pruned AlexNet. Furthermore, recent work has found that quantization-aware pruning generates more computationally efficient models than either pruning or quantization alone; It typically performs similar to or better in terms of computational efficiency compared to other neural architecture search techniques like Bayesian optimization [Ps and Qs: Quantization-Aware Pruning for Efficient Low Latency Neural Network Inference][2021](https://arxiv.org/pdf/2102.11289.pdf).
-
-
-Src: [https://arxiv.org/abs/1510.00149](https://arxiv.org/abs/1510.00149)
+
-
+
### Edge-aware Quantization
-Quantization not only reduces model size but also enables faster computations and draws less power, making it vital to edge development. Edge devices typically have tight resource constraints with compute, memory, and power, which are impossible to meet for many of the deep NN models of today. Furthermore, edge processors do not support floating point operations, making integer quantization particularly important for chips like GAP-8, a RISC-=V SoC for edge inference with a dedicated CNN accelerator, which only support integer arithmetic..
+Quantization not only reduces model size but also enables faster computations and draws less power, making it vital to edge development. Edge devices typically have tight resource constraints with compute, memory, and power, which are impossible to meet for many of the deep NN models of today. Furthermore, edge processors do not support floating point operations, making integer quantization particularly important for chips like GAP-8, a RISC-V SoC for edge inference with a dedicated CNN accelerator, which only support integer arithmetic..
-One hardware platform utilizing quantization is the ARM Cortex-M group of 32=bit RISC ARM processor cores. They leverage fixed-point quantization with power of two scaling factors so that quantization and dequantization can be efficiently done by bit shifting. Additionally, Google Edge TPUs, Google's emerging solution for running inference at the edge, is designed for small, low-powered devices and can only support 8-bit arithmetic. Recently, there has been significant strides in the computing power of edge processors, enabling the deployment and inference of costly NN models previously limited to servers.
+One hardware platform utilizing quantization is the ARM Cortex-M group of 32-bit RISC ARM processor cores. They leverage fixed-point quantization with power of two scaling factors so that quantization and dequantization can be efficiently done by bit shifting. Additionally, Google Edge TPUs, Google's emerging solution for running inference at the edge, is designed for small, low-powered devices and can only support 8-bit arithmetic. Recently, there has been significant strides in the computing power of edge processors, enabling the deployment and inference of costly NN models previously limited to servers.
-
+
In addition to being an indispensable technique for many edge processors, quantization has also brought noteworthy improvements to non-edge processors such as encouraging such processors to meet the Service Level Agreement (SLA) requirements such as 99th percentile latency.
@@ -659,32 +643,30 @@ Efficient hardware implementation transcends the selection of suitable component
### Hardware-Aware Neural Architecture Search
-Focusing only on the accuracy when performing Neural Architecture Search leads to models that are exponentially complex and require increasing memory and compute. This has lead to hardware constraints limiting the exploitation of the deep learning models at their full potential. Manually designing the architecture of the model is even harder when considering the hardware variety and limitations. This has lead to the creation of Hardware-aware Neural Architecture Search that incorporate the hardware contractions into their search and optimize the search space for a specific hardware and accuracy. HW-NAS can be catogrized based how it optimizes for hardware. We will briefly explore these categories and leave links to related papers for the interested reader.
+Focusing only on the accuracy when performing Neural Architecture Search leads to models that are exponentially complex and require increasing memory and compute. This has lead to hardware constraints limiting the exploitation of the deep learning models at their full potential. Manually designing the architecture of the model is even harder when considering the hardware variety and limitations. This has lead to the creation of Hardware-aware Neural Architecture Search that incorporate the hardware contractions into their search and optimize the search space for a specific hardware and accuracy. HW-NAS can be categorized based how it optimizes for hardware. We will briefly explore these categories and leave links to related papers for the interested reader.
-](images/modeloptimization_HW-NAS.png)
+![Taxonomy of HW-NAS [@ijcai2021p592]](images/modeloptimization_HW-NAS.png)
#### Single Target, Fixed Platfrom Configuration
-The goal here is to find the best architecture in terms of accuracy and hardware efficiency for one fixed target hardware. For a specific hardware, the Arduino Nicla Vision for example, this category of HW-NAS will look for the architecture that optimizes accuracy, latency, energy consumption, …
-
-Two approaches fall under this category
+The goal here is to find the best architecture in terms of accuracy and hardware efficiency for one fixed target hardware. For a specific hardware, the Arduino Nicla Vision for example, this category of HW-NAS will look for the architecture that optimizes accuracy, latency, energy consumption, etc.
##### Hardware-aware Search Strategy
-Here, the search is a multi-objective optimization problem, where both the accuracy and hardware cost guide the searching algorithm to find the most efficient architecture. [1](https://openaccess.thecvf.com/content_CVPR_2019/html/Tan_MnasNet_Platform-Aware_Neural_Architecture_Search_for_Mobile_CVPR_2019_paper.html)[2](https://arxiv.org/abs/1812.00332)[3](https://arxiv.org/abs/1812.03443)
+Here, the search is a multi-objective optimization problem, where both the accuracy and hardware cost guide the searching algorithm to find the most efficient architecture [@tan2019mnasnet; @cai2018proxylessnas; @wu2019fbnet].
##### Hardware-aware Search Space
-Here, the search space is restricted to the architectures that perform well on the specific hardware. This can be achieved by either measuring the operators (Conv operator, Pool operator, …) performance, or define a set of rules that limit the search space. [1](https://openaccess.thecvf.com/content_CVPRW_2020/html/w40/Zhang_Fast_Hardware-Aware_Neural_Architecture_Search_CVPRW_2020_paper.html)
+Here, the search space is restricted to the architectures that perform well on the specific hardware. This can be achieved by either measuring the operators (Conv operator, Pool operator, …) performance, or define a set of rules that limit the search space. [@Zhang_2020_CVPR_Workshops]
#### Single Target, Multiple Platform Configurations
-Some hardwares may have different configurations. For example, FPGAs have Configurable Logic Blocks (CLBs) that can be configured by the firmware. This method allows for the HW-NAS to explore different configurations. [1](https://arxiv.org/abs/1901.11211)[2](https://arxiv.org/abs/2002.04116)
+Some hardwares may have different configurations. For example, FPGAs have Configurable Logic Blocks (CLBs) that can be configured by the firmware. This method allows for the HW-NAS to explore different configurations. [@jiang2019accuracy; @yang2020coexploration]
#### Multiple Targets
-This category aims at optimizing a single model for multiple hardwares. This can be helpful for mobile devices development as it can optimize to different phones models. [1](https://arxiv.org/abs/2008.08178)[2](https://ieeexplore.ieee.org/document/9102721)
+This category aims at optimizing a single model for multiple hardwares. This can be helpful for mobile devices development as it can optimize to different phones models. [@chu2021discovering; @jiang2019accuracy]
#### Examples of Hardware-Aware Neural Architecture Search
@@ -694,13 +676,14 @@ TinyNAS adopts a two stage approach to finding an optimal architecture for model
First, TinyNAS generate multiple search spaces by varying the input resolution of the model, and the number of channels of the layers of the model. Then, TinyNAS chooses a search space based on the FLOPs (Floating Point Operations Per Second) of each search space
-Then, TinyNAS performs a search operation on the chosen space to find the optimal architecture for the specific constraints of the microcontroller. [1](https://arxiv.org/abs/2007.10319)
+Then, TinyNAS performs a search operation on the chosen space to find the optimal architecture for the specific constraints of the microcontroller. [@lin2020mcunet]
+
+![A diagram showing how search spaces with high probability of finding an architecture with large number of FLOPs provide models with higher accuracy [@lin2020mcunet]](images/modeloptimization_TinyNAS.png)
-](images/modeloptimization_TinyNAS.png)
#### Topology-Aware NAS
-Focuses on creating and optimizing a search space that aligns with the hardware topology of the device. [1](https://arxiv.org/pdf/1911.09251.pdf)
+Focuses on creating and optimizing a search space that aligns with the hardware topology of the device. [@zhang2019autoshrink]
### Challenges of Hardware-Aware Neural Architecture Search
@@ -728,13 +711,13 @@ Similarly to blocking, tiling divides data and computation into chunks, but exte
##### Optimized Kernel Libraries
-This comprises developing optimized kernels that take full advantage of a specific hardware. One example is the CMSIS-NN library, which is a collection of efficient neural network kernels developed to optimize the performance and minimize the memory footprint of models on Arm Cortex-M processors, which are common on IoT edge devices. The kernel leverage multiple hardware capabilities of Cortex-M processors like Single Instruction Multple Data (SIMD), Floating Point Units (FPUs) and M-Profile Vector Extensions (MVE). These optimization make common operations like matrix multiplications more efficient, boosting the performance of model operations on Cortex-M processors. [1](https://arxiv.org/abs/1801.06601#:~:text=This%20paper%20presents%20CMSIS,for%20intelligent%20IoT%20edge%20devices)
+This comprises developing optimized kernels that take full advantage of a specific hardware. One example is the CMSIS-NN library, which is a collection of efficient neural network kernels developed to optimize the performance and minimize the memory footprint of models on Arm Cortex-M processors, which are common on IoT edge devices. The kernel leverage multiple hardware capabilities of Cortex-M processors like Single Instruction Multple Data (SIMD), Floating Point Units (FPUs) and M-Profile Vector Extensions (MVE). These optimization make common operations like matrix multiplications more efficient, boosting the performance of model operations on Cortex-M processors. [@lai2018cmsisnn]
### Compute-in-Memory (CiM)
-This is one example of Algorithm-Hardware Co-design. CiM is a computing paradigm that performs computation within memory. Therefore, CiM architectures allow for operations to be performed directly on the stored data, without the need to shuttle data back and forth between separate processing and memory units. This design paradigm is particularly beneficial in scenarios where data movement is a primary source of energy consumption and latency, such as in TinyML applications on edge devices. Through algorithm-hardware co-design, the algorithms can be optimized to leverage the unique characteristics of CiM architectures, and conversely, the CiM hardware can be customized or configured to better support the computational requirements and characteristics of the algorithms. This is achieved by using the analog properties of memory cells, such as addition and multiplication in DRAM. [1](https://arxiv.org/abs/2111.06503)
+This is one example of Algorithm-Hardware Co-design. CiM is a computing paradigm that performs computation within memory. Therefore, CiM architectures allow for operations to be performed directly on the stored data, without the need to shuttle data back and forth between separate processing and memory units. This design paradigm is particularly beneficial in scenarios where data movement is a primary source of energy consumption and latency, such as in TinyML applications on edge devices. Through algorithm-hardware co-design, the algorithms can be optimized to leverage the unique characteristics of CiM architectures, and conversely, the CiM hardware can be customized or configured to better support the computational requirements and characteristics of the algorithms. This is achieved by using the analog properties of memory cells, such as addition and multiplication in DRAM. [@zhou2021analognets]
-](images/modeloptimization_CiM.png)
+![A figure showing how Computing in Memory can be used for always-on tasks to offload tasks of the power consuming processing unit [@zhou2021analognets]](images/modeloptimization_CiM.png)
### Memory Access Optimization
@@ -742,30 +725,31 @@ Different devices may have different memory hierarchies. Optimizing for the spec
#### Leveraging Sparsity
-Pruning is a fundamental approach to compress models to make them compatible with resource constrained devices. This results in sparse models where a lot of weights are 0's. Therefore, leveraging this sparsity can lead to significant improvements in performance. Tools were created to achieve exactly this. RAMAN, is a sparseTinyML accelerator designed for inference on edge devices. RAMAN overlap input and output activations on the same memory space, reducing storage requirements by up to 50%. [1](https://ar5iv.labs.arxiv.org/html/2306.06493)
+Pruning is a fundamental approach to compress models to make them compatible with resource constrained devices. This results in sparse models where a lot of weights are 0's. Therefore, leveraging this sparsity can lead to significant improvements in performance. Tools were created to achieve exactly this. RAMAN, is a sparseTinyML accelerator designed for inference on edge devices. RAMAN overlap input and output activations on the same memory space, reducing storage requirements by up to 50%. [@krishna2023raman]
+
+![A figure showing the sparse columns of the filter matrix of a CNN that are aggregated to create a dense matrix that, leading to smaller dimensions in the matrix and more efficient computations. [@kung2018packing]
-](images/modeloptimization_sparsity.png)
#### Optimization Frameworks
Optimization Frameworks have been introduced to exploit the specific capabilities of the hardware to accelerate the software. One example of such a framework is hls4ml. This open-source software-hardware co-design workflow aids in interpreting and translating machine learning algorithms for implementation with both FPGA and ASIC technologies, enhancing their. Features such as network optimization, new Python APIs, quantization-aware pruning, and end-to-end FPGA workflows are embedded into the hls4ml framework, leveraging parallel processing units, memory hierarchies, and specialized instruction sets to optimize models for edge hardware. Moreover, hls4ml is capable of translating machine learning algorithms directly into FPGA firmware.
-](images/modeloptimization_hls4ml.png)
+![A Diagram showing the workflow with the hls4ml framework [@fahim2021hls4ml]](images/modeloptimization_hls4ml.png)
-One other framework for FPGAs that focuses on a holistic approach is CFU Playground [1](https://arxiv.org/abs/2201.01863)
+One other framework for FPGAs that focuses on a holistic approach is CFU Playground [@Prakash_2023]
#### Hardware Built Around Software
-In a contrasting approach, hardware can be custom-designed around software requirements to optimize the performance for a specific application. This paradigm creates specialized hardware to better adapt to the specifics of the software, thus reducing computational overhead and improving operational efficiency. One example of this approach is a voice-recognition application by [1](https://www.mdpi.com/2076-3417/11/22/11073). The paper proposes a structure wherein preprocessing operations, traditionally handled by software, are allocated to custom-designed hardware. This technique was achieved by introducing resistor–transistor logic to an inter-integrated circuit sound module for windowing and audio raw data acquisition in the voice-recognition application. Consequently, this offloading of preprocessing operations led to a reduction in computational load on the software, showcasing a practical application of building hardware around software to enhance the efficiency and performance. [1](https://www.mdpi.com/2076-3417/11/22/11073)
+In a contrasting approach, hardware can be custom-designed around software requirements to optimize the performance for a specific application. This paradigm creates specialized hardware to better adapt to the specifics of the software, thus reducing computational overhead and improving operational efficiency. One example of this approach is a voice-recognition application by [@app112211073]. The paper proposes a structure wherein preprocessing operations, traditionally handled by software, are allocated to custom-designed hardware. This technique was achieved by introducing resistor–transistor logic to an inter-integrated circuit sound module for windowing and audio raw data acquisition in the voice-recognition application. Consequently, this offloading of preprocessing operations led to a reduction in computational load on the software, showcasing a practical application of building hardware around software to enhance the efficiency and performance.
-](images/modeloptimization_preprocessor.png)
+![A diagram showing how an FPGA was used to offload data preprocessing of the general purpose computation unit. [@app112211073]](images/modeloptimization_preprocessor.png)
#### SplitNets
-SplitNets were introduced in the context of Head-Mounted systems. They distribute the Deep Neural Networks (DNNs) workload among camera sensors and an aggregator. This is particularly compelling the in context of TinyML. The SplitNet framework is a split-aware NAS to find the optimal neural network architecture to achieve good accuracy, split the model among the sensors and the aggregator, and minimize the communication between the sensors and the aggregator. Minimal communication is important in TinyML where memory is highly constrained, this way the sensors conduct some of the processing on their chips and then they send only the necessary information to the aggregator. When testing on ImageNet, SplitNets were able to reduce the latency by one order of magnitude on head-mounted devices. This can be helpful when the sensor has it's own chip. [1](https://arxiv.org/pdf/2204.04705.pdf)
+SplitNets were introduced in the context of Head-Mounted systems. They distribute the Deep Neural Networks (DNNs) workload among camera sensors and an aggregator. This is particularly compelling the in context of TinyML. The SplitNet framework is a split-aware NAS to find the optimal neural network architecture to achieve good accuracy, split the model among the sensors and the aggregator, and minimize the communication between the sensors and the aggregator. Minimal communication is important in TinyML where memory is highly constrained, this way the sensors conduct some of the processing on their chips and then they send only the necessary information to the aggregator. When testing on ImageNet, SplitNets were able to reduce the latency by one order of magnitude on head-mounted devices. This can be helpful when the sensor has its own chip. [@dong2022splitnets]
-](images/modeloptimization_SplitNets.png)
+![A chart showing a comparison between the performance of SplitNets vs all on sensor and all on aggregator approaches. [@dong2022splitnets]](images/modeloptimization_SplitNets.png)
#### Hardware Specific Data Augmentation
@@ -798,7 +782,7 @@ Automated optimization tools provided by frameworks can analyze models and autom
- [Pruning](https://www.tensorflow.org/model_optimization/guide/pruning/pruning_with_keras) - Automatically removes unnecessary connections in a model based on analysis of weight importance. Can prune entire filters in convolutional layers or attention heads in transformers. Handles iterative re-training to recover any accuracy loss.
- [GraphOptimizer](https://www.tensorflow.org/guide/graph_optimization) - Applies graph optimizations like operator fusion to consolidate operations and reduce execution latency, especially for inference.
-
+
These automated modules only require the user to provide the original floating point model, and handle the end-to-end optimization pipeline including any re-training to regain accuracy. Other frameworks like PyTorch also offer increasing automation support, for example through torch.quantization.quantize\_dynamic. Automated optimization makes efficient ML accessible to practitioners without optimization expertise.
@@ -811,7 +795,7 @@ Quantization: For example, TensorRT and TensorFlow Lite both support quantizatio
Kernel Optimization: For instance, TensorRT does auto-tuning to optimize CUDA kernels based on the GPU architecture for each layer in the model graph. This extracts maximum throughput.
Operator Fusion: TensorFlow XLA does aggressive fusion to create optimized binary for TPUs. On mobile, frameworks like NCNN also support fused operators.
-
+`
Hardware-Specific Code: Libraries are used to generate optimized binary code specialized for the target hardware. For example, [TensorRT](https://docs.nvidia.com/deeplearning/tensorrt/developer-guide/index.html) uses Nvidia CUDA/cuDNN libraries which are hand-tuned for each GPU architecture. This hardware-specific coding is key for performance. On tinyML devices, this can mean assembly code optimized for a Cortex M4 CPU for example. Vendors provide CMSIS-NN and other libraries.
Data Layout Optimizations - We can efficiently leverage memory hierarchy of hardware like cache and registers through techniques like tensor/weight rearrangement, tiling, and reuse. For example, TensorFlow XLA optimizes buffer layouts to maximize TPU utilization. This helps any memory constrained systems.
@@ -826,13 +810,13 @@ Implementing model optimization techniques without visibility into the effects o
##### Sparsity (ADD SOME LINKS INTO HERE)
-For example, consider sparsity optimizations. Sparsity visualization tools can provide critical insights into pruned models by mapping out exactly which weights have been removed. For example, sparsity heat maps can use color gradients to indicate the percentage of weights pruned in each layer of a neural network. Layers with higher percentages pruned appear darker. This identifies which layers have been simplified the most by pruning.
+For example, consider sparsity optimizations. Sparsity visualization tools can provide critical insights into pruned models by mapping out exactly which weights have been removed. For example, sparsity heat maps can use color gradients to indicate the percentage of weights pruned in each layer of a neural network. Layers with higher percentages pruned appear darker. This identifies which layers have been simplified the most by pruning. (Souza ([2020](https://www.numenta.com/blog/2020/10/30/case-for-sparsity-in-neural-networks-part-2-dynamic-sparsity/)))
-[Figure: maybe consider including an example from Wolfram]
+
Trend plots can also track sparsity over successive pruning rounds - they may show initial rapid pruning followed by more gradual incremental increases. Tracking the current global sparsity along with statistics like average, minimum, and maximum sparsity per-layer in tables or plots provides an overview of the model composition. For a sample convolutional network, these tools could reveal that the first convolution layer is pruned 20% while the final classifier layer is pruned 70% given its redundancy. The global model sparsity may increase from 10% after initial pruning to 40% after five rounds.
-[Figure: Line graph with one line per layer, showing sparsity % over multiple pruning rounds or something to that effet]
+![A figure showing the sparse columns of the filter matrix of a CNN that are aggregated to create a dense matrix that, leading to smaller dimensions in the matrix and more efficient computations [@kung2018packing]](images/modeloptimization_sparsity.png)
By making sparsity data visually accessible, practitioners can better understand exactly how their model is being optimized and which areas are being impacted. The visibility enables them to fine-tune and control the pruning process for a given architecture.
@@ -842,11 +826,11 @@ Sparsity visualization turns pruning into a transparent technique instead of a b
Converting models to lower numeric precisions through quantization introduces errors that can impact model accuracy if not properly tracked and addressed. Visualizing quantization error distributions provides valuable insights into the effects of reduced precision numerics applied to different parts of a model. For this, histograms of the quantization errors for weights and activations can be generated. These histograms can reveal the shape of the error distribution - whether they resemble a Gaussian distribution or contain significant outliers and spikes. Large outliers may indicate issues with particular layers handling the quantization. Comparing the histograms across layers highlights any problem areas standing out with abnormally high errors.
-[Figure: include the example of the histograms, this stuff exists in papers]
+![A smooth histogram of quantization error. [@kuzmin2022fp8]](images/modeloptimization_quant_hist.png)
-Activation visualizations are also important to detect overflow issues. By color mapping the activations before and after quantization, any values pushed outside the intended ranges become visible. This reveals saturation and truncation issues that could skew the information flowing through the model. Detecting these errors allows recalibrating activations to prevent loss of information.
+Activation visualizations are also important to detect overflow issues. By color mapping the activations before and after quantization, any values pushed outside the intended ranges become visible. This reveals saturation and truncation issues that could skew the information flowing through the model. Detecting these errors allows recalibrating activations to prevent loss of information. (Mandal ([2022](https://medium.com/exemplifyml-ai/visualizing-neural-network-activation-a27caa451ff)))
-[Figure: include a color mapping example]
+
Other techniques, such as tracking the overall mean square quantization error at each step of the quantization-aware training process identifies fluctuations and divergences. Sudden spikes in the tracking plot may indicate points where quantization is disrupting the model training. Monitoring this metric builds intuition on model behavior under quantization. Together these techniques turn quantization into a transparent process. The empirical insights enable practitioners to properly assess quantization effects. They pinpoint areas of the model architecture or training process to recalibrate based on observed quantization issues. This helps achieve numerically stable and accurate quantized models.
@@ -862,7 +846,7 @@ TensorFlow Lite - TensorFlow's platform to convert models to a lightweight forma
ONNX Runtime - Performs model conversion and inference for models in the open ONNX model format. Provides optimized kernels, supports hardware accelerators like GPUs, and cross-platform deployment from cloud to edge. Allows framework-agnostic deployment.
-[add figure of ONNX being an interoperable framework]
+
PyTorch Mobile - Enables PyTorch models to be run on iOS and Android by converting to mobile-optimized representations. Provides efficient mobile implementations of ops like convolution and special functions optimized for mobile hardware.
@@ -876,6 +860,6 @@ In this chapter we've discussed model optimization across the software-hardware
We then explored efficient numerics representations, where we covered the basics of numerics, numeric encodings and storage, benefits of efficient numerics, and the nuances of numeric representation with memory usage, computational complexity, hardware compatibility, and tradeoff scenarios. We finished by honing in on an efficient numerics staple: quantization, where we examined its history, calibration, techniques, and interaction with pruning.
-Finally, we looked at how we can make optimizations specific to the hardware we have. We explored how we can find model architectures tailored to the hardware, make optimizations in the kernel to better handle the model, and frameworks built to make the most use out of the hardware. We also looked at how we can go the other way around and build hardware around our specific software and talked about splitting networks to run on multiple processor available on the edge device.
+Finally, we looked at how we can make optimizations specific to the hardware we have. We explored how we can find model architectures tailored to the hardware, make optimizations in the kernel to better handle the model, and frameworks built to make the most use out of the hardware. We also looked at how we can go the other way around and build hardware around our specific software and talked about splitting networks to run on multiple processors available on the edge device.
By understanding the full picture of the degrees of freedom within model optimization both away and close to the hardware and the tradeoffs to consider when implementing these methods, practitioners can develop a more thoughtful pipeline for compressing their workloads onto edge devices.
diff --git a/references.bib b/references.bib
index a25feb47f..4501f577d 100644
--- a/references.bib
+++ b/references.bib
@@ -14,6 +14,98 @@ @article{banbury2020benchmarking
year={2020}
}
+@misc{hinton2015distilling,
+ title={Distilling the Knowledge in a Neural Network},
+ author={Geoffrey Hinton and Oriol Vinyals and Jeff Dean},
+ year={2015},
+ eprint={1503.02531},
+ archivePrefix={arXiv},
+ primaryClass={stat.ML}
+}
+
+@inproceedings{gordon2018morphnet,
+ title={Morphnet: Fast \& simple resource-constrained structure learning of deep networks},
+ author={Gordon, Ariel and Eban, Elad and Nachum, Ofir and Chen, Bo and Wu, Hao and Yang, Tien-Ju and Choi, Edward},
+ booktitle={Proceedings of the IEEE conference on computer vision and pattern recognition},
+ pages={1586--1595},
+ year={2018}
+}
+
+
+@article{lin2020mcunet,
+ title={Mcunet: Tiny deep learning on iot devices},
+ author={Lin, Ji and Chen, Wei-Ming and Lin, Yujun and Gan, Chuang and Han, Song and others},
+ journal={Advances in Neural Information Processing Systems},
+ volume={33},
+ pages={11711--11722},
+ year={2020}
+}
+
+@inproceedings{tan2019mnasnet,
+ title={Mnasnet: Platform-aware neural architecture search for mobile},
+ author={Tan, Mingxing and Chen, Bo and Pang, Ruoming and Vasudevan, Vijay and Sandler, Mark and Howard, Andrew and Le, Quoc V},
+ booktitle={Proceedings of the IEEE/CVF conference on computer vision and pattern recognition},
+ pages={2820--2828},
+ year={2019}
+}
+
+@article{cai2018proxylessnas,
+ title={Proxylessnas: Direct neural architecture search on target task and hardware},
+ author={Cai, Han and Zhu, Ligeng and Han, Song},
+ journal={arXiv preprint arXiv:1812.00332},
+ year={2018}
+}
+
+@inproceedings{wu2019fbnet,
+ title={Fbnet: Hardware-aware efficient convnet design via differentiable neural architecture search},
+ author={Wu, Bichen and Dai, Xiaoliang and Zhang, Peizhao and Wang, Yanghan and Sun, Fei and Wu, Yiming and Tian, Yuandong and Vajda, Peter and Jia, Yangqing and Keutzer, Kurt},
+ booktitle={Proceedings of the IEEE/CVF conference on computer vision and pattern recognition},
+ pages={10734--10742},
+ year={2019}
+}
+
+
+@article{xu2018alternating,
+ title={Alternating multi-bit quantization for recurrent neural networks},
+ author={Xu, Chen and Yao, Jianqiang and Lin, Zhouchen and Ou, Wenwu and Cao, Yuanbin and Wang, Zhirong and Zha, Hongbin},
+ journal={arXiv preprint arXiv:1802.00150},
+ year={2018}
+}
+
+@article{krishnamoorthi2018quantizing,
+ title={Quantizing deep convolutional networks for efficient inference: A whitepaper},
+ author={Krishnamoorthi, Raghuraman},
+ journal={arXiv preprint arXiv:1806.08342},
+ year={2018}
+}
+
+
+@article{iandola2016squeezenet,
+ title={SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size},
+ author={Iandola, Forrest N and Han, Song and Moskewicz, Matthew W and Ashraf, Khalid and Dally, William J and Keutzer, Kurt},
+ journal={arXiv preprint arXiv:1602.07360},
+ year={2016}
+}
+
+
+@misc{tan2020efficientnet,
+ title={EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks},
+ author={Mingxing Tan and Quoc V. Le},
+ year={2020},
+ eprint={1905.11946},
+ archivePrefix={arXiv},
+ primaryClass={cs.LG}
+}
+
+@misc{howard2017mobilenets,
+ title={MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications},
+ author={Andrew G. Howard and Menglong Zhu and Bo Chen and Dmitry Kalenichenko and Weijun Wang and Tobias Weyand and Marco Andreetto and Hartwig Adam},
+ year={2017},
+ eprint={1704.04861},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV}
+}
+
@inproceedings{hendrycks2021natural,
title={Natural adversarial examples},
author={Hendrycks, Dan and Zhao, Kevin and Basart, Steven and Steinhardt, Jacob and Song, Dawn},
@@ -694,13 +786,17 @@ @article{qi_efficient_2021
@misc{noauthor_knowledge_nodate,
title = {Knowledge {Distillation} - {Neural} {Network} {Distiller}},
url = {https://intellabs.github.io/distiller/knowledge_distillation.html},
+ author = {IntelLabs},
urldate = {2023-10-20},
+ year = {2023}
}
@misc{noauthor_deep_nodate,
title = {Deep {Learning} {Model} {Compression} (ii) {\textbar} by {Ivy} {Gu} {\textbar} {Medium}},
url = {https://ivygdy.medium.com/deep-learning-model-compression-ii-546352ea9453},
urldate = {2023-10-20},
+ author = {Ivy Gu},
+ year = {2023}
}
@misc{lu_notes_2016,
@@ -780,6 +876,8 @@ @misc{noauthor_introduction_nodate
title = {An {Introduction} to {Separable} {Convolutions} - {Analytics} {Vidhya}},
url = {https://www.analyticsvidhya.com/blog/2021/11/an-introduction-to-separable-convolutions/},
urldate = {2023-10-20},
+ author = {Hegde, Sumant},
+ year = {2023}
}
@misc{iandola_squeezenet_2016,
@@ -982,3 +1080,240 @@ @inproceedings{coleman2022similarity
pages={6402--6410},
year={2022}
}
+@misc{threefloat,
+ title = {Three Floating Point Formats},
+ url = {https://storage.googleapis.com/gweb-cloudblog-publish/images/Three_floating-point_formats.max-624x261.png},
+ urldate = {2023-10-20},
+ author = {Google},
+ year = {2023}
+}
+@misc{energyproblem,
+ title = {Computing's energy problem (and what we can do about it)},
+ url = {https://ieeexplore.ieee.org/document/6757323},
+ urldate = {2014-03-06},
+ author = {ISSCC},
+ year = {2014}
+}
+@misc{surveyofquant,
+ title = {A Survey of Quantization Methods for Efficient Neural Network Inference)},
+ url = {https://arxiv.org/abs/2103.13630},
+ urldate = {2021-06-21},
+ author = {Gholami and Kim, Dong and Yao, Mahoney and Keutzer},
+ year = {2021},
+ doi = {10.48550/arXiv.2103.13630},
+ abstract = {As soon as abstract mathematical computations were adapted to computation on digital computers, the problem of efficient representation, manipulation, and communication of the numerical values in those computations arose. Strongly related to the problem of numerical representation is the problem of quantization: in what manner should a set of continuous real-valued numbers be distributed over a fixed discrete set of numbers to minimize the number of bits required and also to maximize the accuracy of the attendant computations? This perennial problem of quantization is particularly relevant whenever memory and/or computational resources are severely restricted, and it has come to the forefront in recent years due to the remarkable performance of Neural Network models in computer vision, natural language processing, and related areas. Moving from floating-point representations to low-precision fixed integer values represented in four bits or less holds the potential to reduce the memory footprint and latency by a factor of 16x; and, in fact, reductions of 4x to 8x are often realized in practice in these applications. Thus, it is not surprising that quantization has emerged recently as an important and very active sub-area of research in the efficient implementation of computations associated with Neural Networks. In this article, we survey approaches to the problem of quantizing the numerical values in deep Neural Network computations, covering the advantages/disadvantages of current methods. With this survey and its organization, we hope to have presented a useful snapshot of the current research in quantization for Neural Networks and to have given an intelligent organization to ease the evaluation of future research in this area.},
+}
+@misc{intquantfordeepinf,
+ title = {Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation)},
+ url = {https://arxiv.org/abs/2004.09602},
+ urldate = {2020-04-20},
+ author = {Wu and Judd, Zhang and Isaev, Micikevicius},
+ year = {2020},
+ doi = {10.48550/arXiv.2004.09602},
+ abstract = {Quantization techniques can reduce the size of Deep Neural Networks and improve inference latency and throughput by taking advantage of high throughput integer instructions. In this paper we review the mathematical aspects of quantization parameters and evaluate their choices on a wide range of neural network models for different application domains, including vision, speech, and language. We focus on quantization techniques that are amenable to acceleration by processors with high-throughput integer math pipelines. We also present a workflow for 8-bit quantization that is able to maintain accuracy within 1% of the floating-point baseline on all networks studied, including models that are more difficult to quantize, such as MobileNets and BERT-large.},
+}
+@misc{deci,
+ title = {The Ultimate Guide to Deep Learning Model Quantization and Quantization-Aware Training},
+ url = {https://deci.ai/quantization-and-quantization-aware-training/},
+}
+@misc{awq,
+ title = {AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration},
+ url = {https://arxiv.org/abs/2306.00978},
+ urldate = {2023-10-03},
+ author = {Lin and Tang, Tang and Yang, Dang and Gan, Han},
+ year = {2023},
+ doi = {10.48550/arXiv.2306.00978},
+ abstract = {Large language models (LLMs) have shown excellent performance on various tasks, but the astronomical model size raises the hardware barrier for serving (memory size) and slows down token generation (memory bandwidth). In this paper, we propose Activation-aware Weight Quantization (AWQ), a hardware-friendly approach for LLM low-bit weight-only quantization. Our method is based on the observation that weights are not equally important: protecting only 1% of salient weights can greatly reduce quantization error. We then propose to search for the optimal perchannel scaling that protects the salient weights by observing the activation, not weights. AWQ does not rely on any backpropagation or reconstruction, so it can well preserve LLMs’ generalization ability on different domains and modalities, without overfitting to the calibration set. AWQ outperforms existing work on various language modeling and domain-specific benchmarks. Thanks to better generalization, it achieves excellent quantization performance for instruction-tuned LMs and, for the first time, multi-modal LMs. Alongside AWQ, we implement an efficient and flexible inference framework tailored for LLMs on the edge, offering more than 3× speedup over the Huggingface FP16 implementation on both desktop and mobile GPUs. It also democratizes the deployment of the 70B Llama-2 model on mobile GPU (NVIDIA Jetson Orin 64GB).},
+}
+@misc{smoothquant,
+ title = {SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models},
+ url = {https://arxiv.org/abs/2211.10438},
+ urldate = {2023-06-05},
+ author = {Xiao and Lin, Seznec and Wu, Demouth and Han},
+ year = {2023},
+ doi = {10.48550/arXiv.2211.10438},
+ abstract = {Large language models (LLMs) show excellent performance but are compute- and memory-intensive. Quantization can reduce memory and accelerate inference. However, existing methods cannot maintain accuracy and hardware efficiency at the same time. We propose SmoothQuant, a training-free, accuracy-preserving, and general-purpose post-training quantization (PTQ) solution to enable 8-bit weight, 8-bit activation (W8A8) quantization for LLMs. Based on the fact that weights are easy to quantize while activations are not, SmoothQuant smooths the activation outliers by offline migrating the quantization difficulty from activations to weights with a mathematically equivalent transformation. SmoothQuant enables an INT8 quantization of both weights and activations for all the matrix multiplications in LLMs, including OPT, BLOOM, GLM, MT-NLG, and LLaMA family. We demonstrate up to 1.56x speedup and 2x memory reduction for LLMs with negligible loss in accuracy. SmoothQuant enables serving 530B LLM within a single node. Our work offers a turn-key solution that reduces hardware costs and democratizes LLMs.},
+}
+@misc{deepcompress,
+ title = {Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding},
+ url = {https://arxiv.org/abs/1510.00149},
+ urldate = {2016-02-15},
+ author = {Han and Mao and Dally},
+ year = {2016},
+ doi = {10.48550/arXiv.1510.00149},
+ abstract = {Neural networks are both computationally intensive and memory intensive, making them difficult to deploy on embedded systems with limited hardware resources. To address this limitation, we introduce "deep compression", a three stage pipeline: pruning, trained quantization and Huffman coding, that work together to reduce the storage requirement of neural networks by 35x to 49x without affecting their accuracy. Our method first prunes the network by learning only the important connections. Next, we quantize the weights to enforce weight sharing, finally, we apply Huffman coding. After the first two steps we retrain the network to fine tune the remaining connections and the quantized centroids. Pruning, reduces the number of connections by 9x to 13x; Quantization then reduces the number of bits that represent each connection from 32 to 5. On the ImageNet dataset, our method reduced the storage required by AlexNet by 35x, from 240MB to 6.9MB, without loss of accuracy. Our method reduced the size of VGG-16 by 49x from 552MB to 11.3MB, again with no loss of accuracy. This allows fitting the model into on-chip SRAM cache rather than off-chip DRAM memory. Our compression method also facilitates the use of complex neural networks in mobile applications where application size and download bandwidth are constrained. Benchmarked on CPU, GPU and mobile GPU, compressed network has 3x to 4x layerwise speedup and 3x to 7x better energy efficiency.},
+}
+@misc{quantdeep,
+ title = {Quantizing deep convolutional networks for efficient inference: A whitepaper},
+ url = {https://arxiv.org/abs/1806.08342},
+ doi = {10.48550/arXiv.1806.08342},
+ abstract = {We present an overview of techniques for quantizing convolutional neural networks for inference with integer weights and activations. Per-channel quantization of weights and per-layer quantization of activations to 8-bits of precision post-training produces classification accuracies within 2% of floating point networks for a wide variety of CNN architectures. Model sizes can be reduced by a factor of 4 by quantizing weights to 8-bits, even when 8-bit arithmetic is not supported. This can be achieved with simple, post training quantization of weights.We benchmark latencies of quantized networks on CPUs and DSPs and observe a speedup of 2x-3x for quantized implementations compared to floating point on CPUs. Speedups of up to 10x are observed on specialized processors with fixed point SIMD capabilities, like the Qualcomm QDSPs with HVX. Quantization-aware training can provide further improvements, reducing the gap to floating point to 1% at 8-bit precision. Quantization-aware training also allows for reducing the precision of weights to four bits with accuracy losses ranging from 2% to 10%, with higher accuracy drop for smaller networks.We introduce tools in TensorFlow and TensorFlowLite for quantizing convolutional networks and review best practices for quantization-aware training to obtain high accuracy with quantized weights and activations. We recommend that per-channel quantization of weights and per-layer quantization of activations be the preferred quantization scheme for hardware acceleration and kernel optimization. We also propose that future processors and hardware accelerators for optimized inference support precisions of 4, 8 and 16 bits.},
+ urldate = {2018-06-21},
+ publisher = {arXiv},
+ author = {Krishnamoorthi},
+ month = jun,
+ year = {2018},
+}
+@inproceedings{ijcai2021p592,
+ title = {Hardware-Aware Neural Architecture Search: Survey and Taxonomy},
+ author = {Benmeziane, Hadjer and El Maghraoui, Kaoutar and Ouarnoughi, Hamza and Niar, Smail and Wistuba, Martin and Wang, Naigang},
+ booktitle = {Proceedings of the Thirtieth International Joint Conference on
+ Artificial Intelligence, {IJCAI-21}},
+ publisher = {International Joint Conferences on Artificial Intelligence Organization},
+ editor = {Zhi-Hua Zhou},
+ pages = {4322--4329},
+ year = {2021},
+ month = {8},
+ note = {Survey Track},
+ doi = {10.24963/ijcai.2021/592},
+ url = {https://doi.org/10.24963/ijcai.2021/592},
+}
+
+@InProceedings{Zhang_2020_CVPR_Workshops,
+author = {Zhang, Li Lyna and Yang, Yuqing and Jiang, Yuhang and Zhu, Wenwu and Liu, Yunxin},
+title = {Fast Hardware-Aware Neural Architecture Search},
+booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops},
+month = {June},
+year = {2020}
+}
+
+@misc{jiang2019accuracy,
+ title={Accuracy vs. Efficiency: Achieving Both through FPGA-Implementation Aware Neural Architecture Search},
+ author={Weiwen Jiang and Xinyi Zhang and Edwin H. -M. Sha and Lei Yang and Qingfeng Zhuge and Yiyu Shi and Jingtong Hu},
+ year={2019},
+ eprint={1901.11211},
+ archivePrefix={arXiv},
+ primaryClass={cs.DC}
+}
+
+@misc{yang2020coexploration,
+ title={Co-Exploration of Neural Architectures and Heterogeneous ASIC Accelerator Designs Targeting Multiple Tasks},
+ author={Lei Yang and Zheyu Yan and Meng Li and Hyoukjun Kwon and Liangzhen Lai and Tushar Krishna and Vikas Chandra and Weiwen Jiang and Yiyu Shi},
+ year={2020},
+ eprint={2002.04116},
+ archivePrefix={arXiv},
+ primaryClass={cs.LG}
+}
+
+@misc{chu2021discovering,
+ title={Discovering Multi-Hardware Mobile Models via Architecture Search},
+ author={Grace Chu and Okan Arikan and Gabriel Bender and Weijun Wang and Achille Brighton and Pieter-Jan Kindermans and Hanxiao Liu and Berkin Akin and Suyog Gupta and Andrew Howard},
+ year={2021},
+ eprint={2008.08178},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV}
+}
+
+@misc{lin2020mcunet,
+ title={MCUNet: Tiny Deep Learning on IoT Devices},
+ author={Ji Lin and Wei-Ming Chen and Yujun Lin and John Cohn and Chuang Gan and Song Han},
+ year={2020},
+ eprint={2007.10319},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV}
+}
+
+@misc{zhang2019autoshrink,
+ title={AutoShrink: A Topology-aware NAS for Discovering Efficient Neural Architecture},
+ author={Tunhou Zhang and Hsin-Pai Cheng and Zhenwen Li and Feng Yan and Chengyu Huang and Hai Li and Yiran Chen},
+ year={2019},
+ eprint={1911.09251},
+ archivePrefix={arXiv},
+ primaryClass={cs.LG}
+}
+
+@misc{lai2018cmsisnn,
+ title={CMSIS-NN: Efficient Neural Network Kernels for Arm Cortex-M CPUs},
+ author={Liangzhen Lai and Naveen Suda and Vikas Chandra},
+ year={2018},
+ eprint={1801.06601},
+ archivePrefix={arXiv},
+ primaryClass={cs.NE}
+}
+
+@misc{zhou2021analognets,
+ title={AnalogNets: ML-HW Co-Design of Noise-robust TinyML Models and Always-On Analog Compute-in-Memory Accelerator},
+ author={Chuteng Zhou and Fernando Garcia Redondo and Julian Büchel and Irem Boybat and Xavier Timoneda Comas and S. R. Nandakumar and Shidhartha Das and Abu Sebastian and Manuel Le Gallo and Paul N. Whatmough},
+ year={2021},
+ eprint={2111.06503},
+ archivePrefix={arXiv},
+ primaryClass={cs.AR}
+}
+
+@misc{krishna2023raman,
+ title={RAMAN: A Re-configurable and Sparse tinyML Accelerator for Inference on Edge},
+ author={Adithya Krishna and Srikanth Rohit Nudurupati and Chandana D G and Pritesh Dwivedi and André van Schaik and Mahesh Mehendale and Chetan Singh Thakur},
+ year={2023},
+ eprint={2306.06493},
+ archivePrefix={arXiv},
+ primaryClass={cs.NE}
+}
+
+@misc{kung2018packing,
+ title={Packing Sparse Convolutional Neural Networks for Efficient Systolic Array Implementations: Column Combining Under Joint Optimization},
+ author={H. T. Kung and Bradley McDanel and Sai Qian Zhang},
+ year={2018},
+ eprint={1811.04770},
+ archivePrefix={arXiv},
+ primaryClass={cs.LG}
+}
+
+@misc{fahim2021hls4ml,
+ title={hls4ml: An Open-Source Codesign Workflow to Empower Scientific Low-Power Machine Learning Devices},
+ author={Farah Fahim and Benjamin Hawks and Christian Herwig and James Hirschauer and Sergo Jindariani and Nhan Tran and Luca P. Carloni and Giuseppe Di Guglielmo and Philip Harris and Jeffrey Krupa and Dylan Rankin and Manuel Blanco Valentin and Josiah Hester and Yingyi Luo and John Mamish and Seda Orgrenci-Memik and Thea Aarrestad and Hamza Javed and Vladimir Loncar and Maurizio Pierini and Adrian Alan Pol and Sioni Summers and Javier Duarte and Scott Hauck and Shih-Chieh Hsu and Jennifer Ngadiuba and Mia Liu and Duc Hoang and Edward Kreinar and Zhenbin Wu},
+ year={2021},
+ eprint={2103.05579},
+ archivePrefix={arXiv},
+ primaryClass={cs.LG}
+}
+
+@inproceedings{Prakash_2023,
+ doi = {10.1109/ispass57527.2023.00024},
+
+ url = {https://doi.org/10.1109%2Fispass57527.2023.00024},
+
+ year = 2023,
+ month = {apr},
+
+ publisher = {{IEEE}
+},
+
+ author = {Shvetank Prakash and Tim Callahan and Joseph Bushagour and Colby Banbury and Alan V. Green and Pete Warden and Tim Ansell and Vijay Janapa Reddi},
+
+ title = {{CFU} Playground: Full-Stack Open-Source Framework for Tiny Machine Learning ({TinyML}) Acceleration on {FPGAs}},
+
+ booktitle = {2023 {IEEE} International Symposium on Performance Analysis of Systems and Software ({ISPASS})}
+}
+
+
+@Article{app112211073,
+AUTHOR = {Kwon, Jisu and Park, Daejin},
+TITLE = {Hardware/Software Co-Design for TinyML Voice-Recognition Application on Resource Frugal Edge Devices},
+JOURNAL = {Applied Sciences},
+VOLUME = {11},
+YEAR = {2021},
+NUMBER = {22},
+ARTICLE-NUMBER = {11073},
+URL = {https://www.mdpi.com/2076-3417/11/22/11073},
+ISSN = {2076-3417},
+ABSTRACT = {On-device artificial intelligence has attracted attention globally, and attempts to combine the internet of things and TinyML (machine learning) applications are increasing. Although most edge devices have limited resources, time and energy costs are important when running TinyML applications. In this paper, we propose a structure in which the part that preprocesses externally input data in the TinyML application is distributed to the hardware. These processes are performed using software in the microcontroller unit of an edge device. Furthermore, resistor–transistor logic, which perform not only windowing using the Hann function, but also acquire audio raw data, is added to the inter-integrated circuit sound module that collects audio data in the voice-recognition application. As a result of the experiment, the windowing function was excluded from the TinyML application of the embedded board. When the length of the hardware-implemented Hann window is 80 and the quantization degree is 2−5, the exclusion causes a decrease in the execution time of the front-end function and energy consumption by 8.06% and 3.27%, respectively.},
+DOI = {10.3390/app112211073}
+}
+
+@misc{dong2022splitnets,
+ title={SplitNets: Designing Neural Architectures for Efficient Distributed Computing on Head-Mounted Systems},
+ author={Xin Dong and Barbara De Salvo and Meng Li and Chiao Liu and Zhongnan Qu and H. T. Kung and Ziyun Li},
+ year={2022},
+ eprint={2204.04705},
+ archivePrefix={arXiv},
+ primaryClass={cs.LG}
+}
+
+@misc{kuzmin2022fp8,
+ title={FP8 Quantization: The Power of the Exponent},
+ author={Andrey Kuzmin and Mart Van Baalen and Yuwei Ren and Markus Nagel and Jorn Peters and Tijmen Blankevoort},
+ year={2022},
+ eprint={2208.09225},
+ archivePrefix={arXiv},
+ primaryClass={cs.LG}
+}
\ No newline at end of file