Skip to content

Latest commit

 

History

History
222 lines (175 loc) · 5.55 KB

README.md

File metadata and controls

222 lines (175 loc) · 5.55 KB

11. 盛最多水的容器

English Version

题目描述

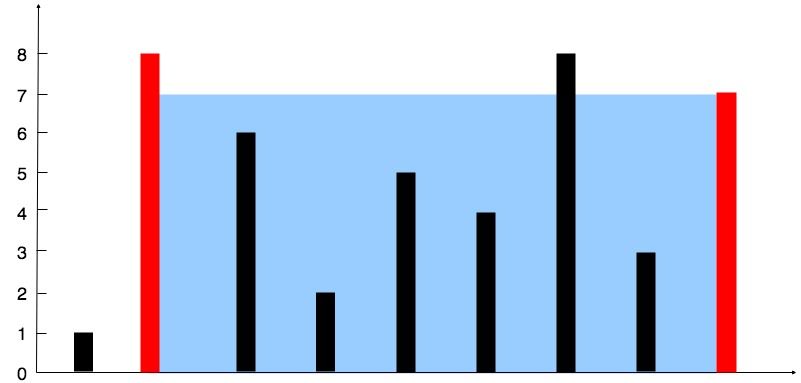
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

 

示例 1：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

 

提示：

  • n == height.length
  • 2 <= n <= 105
  • 0 <= height[i] <= 104

解法

双指针解决。

一开始，我们考虑相距最远的两个柱子所能容纳水的面积。水的宽度是两根柱子之间的距离，而水的高度取决于两根柱子之间较短的那个。

  • 当前柱子是最两侧的柱子，水的宽度最大，其他的组合，水的宽度都比这个小；
  • 当前左侧柱子较短，决定了水的高度。如果移动左侧的柱子，新的水面高度不确定，但一定不会超过右侧的柱子高度；
  • 如果移动右侧的柱子，新的水面高度一定不会超过左侧的柱子高度，也就是不会超过当前的水面高度。

可见，如果固定左侧的柱子，向内移动右侧的柱子，水的高度一定不会增加，且宽度一定减少，所以水的面积一定减少。所以左侧的柱子跟右侧其他柱子的组合，都可以排除了。也就是代码中的 i++。

移动左侧的柱子中，重复进行上面的操作。

在此过程中，我们不断排除掉无法成为构成最大值的柱子组合，而每一次都获取到可能为最大值的面积 t。那么遍历结束之后，我们就可以得到最大值。

Python3

class Solution:
    def maxArea(self, height: List[int]) -> int:
        i, j = 0, len(height) - 1
        res = 0
        while i < j:
            t = (j - i) * min(height[i], height[j])
            res = max(res, t)
            if height[i] < height[j]:
                i += 1
            else:
                j -= 1
        return res

Java

class Solution {
    public int maxArea(int[] height) {
        int i = 0, j = height.length - 1;
        int res = 0;
        while (i < j) {
            int t = (j - i) * Math.min(height[i], height[j]);
            res = Math.max(res, t);
            if (height[i] < height[j]) ++i;
            else --j;
        }
        return res;
    }
}

C++

class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1;
        int res = 0;
        while (i < j) {
            int t = (j - i) * min(height[i], height[j]);
            res = max(res, t);
            if (height[i] < height[j]) ++i;
            else --j;
        }
        return res;
    }
};

Go

func maxArea(height []int) int {
    i, j := 0, len(height) - 1
    res := 0
    for i != j {
        t := (j - i) * min(height[i], height[j])
        res = max(res, t)
        if height[i] < height[j] {
            i++
        } else {
            j--
        }
    }
    return res
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

JavaScript

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function (height) {
    let i = 0,
        j = height.length - 1;
    let res = 0;
    while (i < j) {
        const t = (j - i) * Math.min(height[i], height[j]);
        res = Math.max(res, t);
        if (height[i] < height[j]) ++i;
        else --j;
    }
    return res;
};

TypeScript

function maxArea(height: number[]): number {
    const n = height.length;
    let res = 0;
    for (let i = 0; i < n - 1; i++) {
        for (let j = n - 1; j >= 0; j--) {
            if (height[i] * (j - i) < res) {
                break;
            }
            res = Math.max(res, Math.min(height[i], height[j]) * (j - i));
        }
    }
    return res;
}

Rust

impl Solution {
    pub fn max_area(height: Vec<i32>) -> i32 {
        let mut i = 0;
        let mut j = height.len() - 1;
        let mut res = 0;
        while i < j {
            res = res.max(height[i].min(height[j]) * (j - i) as i32);
            if height[i] <= height[j] {
                i += 1;
            } else {
                j -= 1;
            }
        }
        res
    }
}

...