README.rst

knnpe: A Python package implementing the k-nearest neighbor permutation entropy

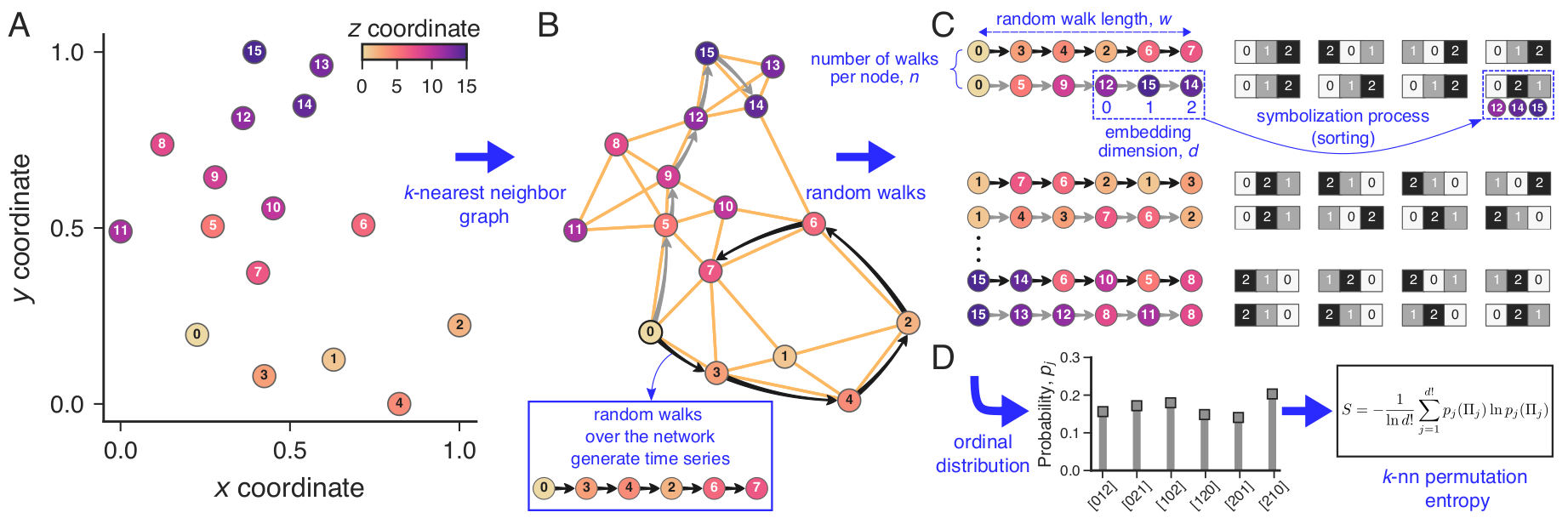
The k-nearest neighbor permutation entropy [1] extends the fundamental premise of investigating the relative ordering of time series elements [2] or image pixels [3] inaugurated by permutation entropy to unstructured datasets. This method builds upon nearest neighbor graphs to establish neighborhood relations among data points and uses random walks over these graphs to extract ordinal patterns and their distribution, thereby defining the $k$-nearest neighbor permutation entropy.

If you have used knnpe in a scientific publication, we would appreciate citations to the following reference:

• L. G. J. M. Voltarelli, A. A. B. Pessa, L. Zunino, R. S. Zola, E. K. Lenzi, M. Perc, H. V. Ribeiro, Characterizing unstructured data with the nearest neighbor permutation entropy, Chaos 34, 053130 (2024). arXiv:2403.13122

@article{voltarelli2024characterizing,
 title         = {Characterizing unstructured data with the nearest neighbor permutation entropy},
 author        = {L. G. J. M. Voltarelli, A. A. B. Pessa, L. Zunino, R. S. Zola, E. K. Lenzi, M. Perc, H. V. Ribeiro},
 journal       = {Chaos},
 volume        = {34},
 pages         = {053130},
 year          = {2024},
 doi           = {10.1063/5.0209206},
}

Installing

knnpe uses OpenMP and GNU Scientific Library (GSL) to implement a parallelized numerically efficient random walk function. This function is written in C and it is integrated with our Python module via the ctypes library. To use this function, you must have OpenMP and GSL installed before installing knnpe.

In Ubuntu/Debian, you can install these dependencies via apt:

sudo apt install build-essential
sudo apt install libgsl-dev
sudo apt install libomp-dev

If these dependencies are not available, knnpe will use a native Python function to do the random walks. This function is also parallelized and may work nicely for most applications; still, it is significantly slower than its C counterpart. For large datasets, we strongly recommend using the C version.

If all dependencies are available, knnpe can be installed via:

pip install git+https://github.com/hvribeiro/knnpe

or

git clone https://github.com/hvribeiro/knnpe.git
cd knnpe
pip install -e .

If all dependencies are not available, you can use the PyPI version via:

pip install knnpe

Basic usage

Implementation of the $k$-nearest neighbor permutation entropy. (A) Illustration of a dataset with irregularly distributed data points $\{z_i\}_{i=1,\dots,N}$ in the $xy$-plane where each coordinate pair $(x_i,y_i)$ is associated with a value $z_i$. (B) Initially, we construct a $k$-nearest neighbor graph using the data coordinates to define neighborhood relationships. In this graph, each data point $z_i$ represents a node, with undirected edges connecting pairs $i\leftrightarrow j$ when $j$ is among the $k$-nearest neighbors of $i$ ($k=3$ in this example). (C) Subsequently, we execute $n$ biased random walks of length $w$ starting from each node, sampling the data points to generate time series ($n=2$ and $w=6$ in this example). We then apply the Bandt-Pompe approach to each of these time series. This involves creating overlapping partitions of length $d$ (embedding dimension) and arranging the partition indices in ascending order of their values to determine the sorting permutations for each partition ($d=3$ in this example). (D) Finally, we evaluate the probability of each of the $d!$ possible permutations (ordinal distribution) and calculate its Shannon entropy, thereby defining the $k$-nearest neighbor permutation entropy.

The function knn_permutation_entropy of knnpe calculates $k$-nearest neighbor permutation entropy as illustrated below for a random dataset with three columns.

import numpy as np
from knnpe import knn_permutation_entropy

data = np.random.normal(size=(100,3))
knn_permutation_entropy(data)

The last column in data corresponds to $\{z_i\}_{i=1,\dots,N}$ values, while the first two columns are used as the data coordinates $\vec{r}_i = (x_i,y_i)$. If the dataset has more dimensions in data coordinates, they must be passed as the first columns of the dataset, and the last column is always assumed to correspond to $z_i$ values. The code below illustrates the case of data with three dimensions in data coordinates:

import numpy as np
from knnpe import knn_permutation_entropy

data = np.random.normal(size=(100,4))
knn_permutation_entropy(data)

The function knn_permutation_entropy has the following parameters:

data : ndarray

Input array containing unstructured data points, where each row is in the form [x, y, value].

d : int, optional

The embedding dimension for the entropy calculation (default is 3).

tau : int, optional

The embedding delay for the entropy calculation (default is 1).

p : float, optional

Parameter that controls the bias of immediately revisiting a node in the walk (default is 10). It is named {\\lambda} in the article.

q : float, optional

Parameter that controls the bias of moving outside the neighborhood of the previous node (default is 0.001). It is named {\\beta} in the article.

random_walk_steps : int, optional

The number of steps in each random walk (default is 10).

num_walks : int, optional

The number of random walk samples to start from each node (default is 10).

n_neighbors : int or array-like, optional

The number of neighbors for constructing the k-nearest neighbor graph (default is 25).

nthreads : int, optional

The number of parallel threads for the computation (default is -1, which uses all available cores).

hide_bar : bool, optional

If True, the progress bar is not displayed (default is False).

metrics : bool, optional

If True, calculates graph density and largest component fraction (default is False).

complexity : bool, optional

If True, also calculates the knn permutation complexity.

We provide a notebook illustrating how to use knnpe and further information we refer to the knnpe's documentation

Contributing

Pull requests addressing errors or adding new functionalities are always welcome.

References

[1]	L. G. J. M. Voltarelli, A. A. B. Pessa, L. Zunino, R. S. Zola, E. K. Lenzi, M. Perc, H. V. Ribeiro. Characterizing unstructured data with the nearest neighbor permutation entropy. Chaos, (Accepted, 2024).

[2]	C. Bandt, B. Pompe. Permutation entropy: A Natural Complexity Measure for Time Series. Physical Review Letters 88, 174102 (2002).

[3]	H. V. Ribeiro, L. Zunino, E. K. Lenzi, P. A. Santoro, R. S. Mendes. Complexity-Entropy Causality Plane as a Complexity Measure for Two-Dimensional Patterns. PLOS ONE 7, e40689 (2012).