LeetCode 45跳跃游戏.md

LeetCode 45跳跃游戏

题目描述：

给定一个非负整数数组，你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

输入: [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。 说明: 假设你总是可以到达数组的最后一个位置。

分析：

这题的话也是运用了不同的方法，从复杂到简单。

法一：枚举

枚举的思路很简单，二重循环，第一次循环遍历每个数，第二次循环遍历长度更新这个范围内能够更新到的最小跳数。如果能跳到该位置并且跳跃次数更少就更新。算法想法简单，初始需要将除第0位其他设置为非常大的值(以便有更小的值进行更新)

实现代码为：

 public  int jump(int[] nums) {
	  int dp[]=new int[nums.length];
	  for(int i=1;i<nums.length;i++)
	  {
		  dp[i]=Integer.MAX_VALUE;
	  }
	  for(int i=0;i<nums.length;i++)
	  {
		  int time=dp[i]+1;
		 
		  for(int j=0;j<nums[i];j++)
		  {
			  if(j+i+1<nums.length)
			  {
				  if(dp[j+i+1]>time)
					  dp[j+i+1]=time;
			  }
		  }
	  }
	  //System.out.println(Arrays.toString(dp));
	  return dp[nums.length-1];
}

不过效果很糟糕。

法二：bfs 在这条路行不通之后，就开始寻找另一条路。我便想着用优先队列搜素，具体比较麻烦详细可以看代码，主要讲第三种方法：

class node
{
	int time;
	int index;
	public node(int time,int index) {
		this.time=time;
		this.index=index;
	}
}
 public  int jump(int[] nums) {
	
	 boolean jud[]=new boolean[nums.length];
	 Queue<node>q1=new PriorityQueue<node>(new Comparator<node>() {
		    @Override
			public int compare(node o1, node o2) {
				if(o1.time==o2.time)
				{
					return o2.index-o1.index;
				}
				return o1.time-o2.time;
			}
	});
	 q1.add(new node(0, 0));
	 while (!q1.isEmpty()) {
		node team=q1.poll();
		int time=team.time+1;
		int index=team.index;
		for(int i=1;i<=nums[index];i++)//前进的位置
		{
			if(index+i<nums.length&&!jud[index+i])
			{
				if(index+i==nums.length-1)return time;
				q1.add(new node(time, index+i));
				jud[index+i]=true;
			}
		}
	}
	 return 0;
 }

法三：贪心 当我以为9ms很快的时候，发现原来这个速度还是很慢，就想肯定有一种近O(n)的方法，在这里索性分享给大家。

我们在这里需要的实什么?

• 找到最少的跳跃次数到达最后

影响我们正常计算的最大障碍是什么？

• 重复计算、覆盖情况.无论是跳跃方式和跳跃次数到达终点都可能不止一种。

但是有一点非常重要的是：每个节点跳跃的时候是一个从他开始的覆盖区间范围，所以我们能否知道第一次跳多远。第二次跳多远呢？第三次呢？

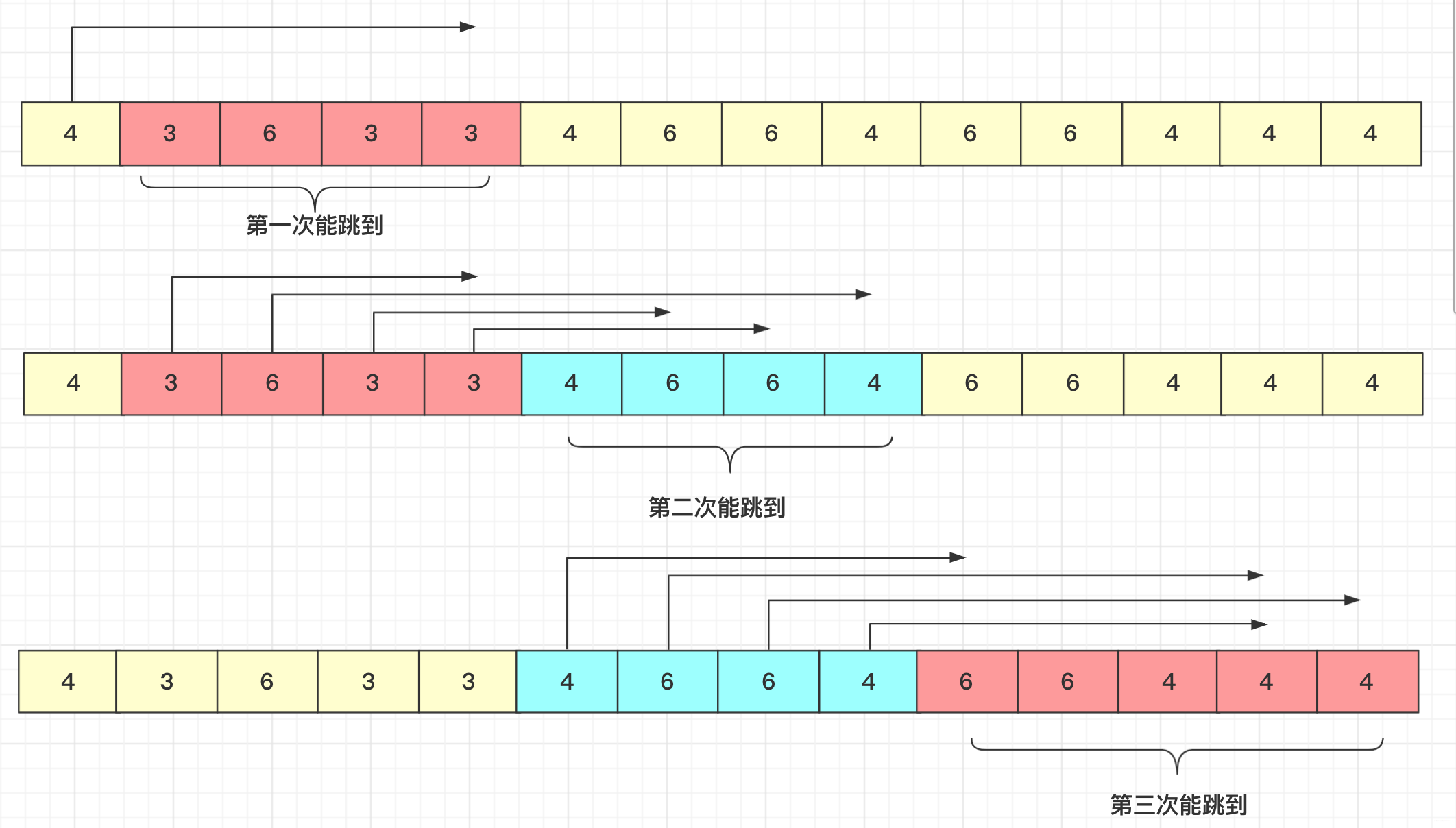
很简单，所有的起始点是0号位置，也就是第一次一定是从0号跳到的一个区间节点。而第二次就是这个区间内能够跳到的最远距离都是2次，第三次就是除掉第二次节点后面能够跳到的区间……这样一直到能够覆盖到最后即可完成。

在具体实现的时候，记录当前的最大长度，用一个time[]数组表示到达当前节点需要的跳数，从前往后，如果最大长度大于当前的maxsize，就说明需要加一次更新，如果小于等于maxsize，对应位置则不需要更新。

实现代码为：

public  int jump(int[] nums) {
	int len=nums.length;
	int time[]=new int[len];
	
	int maxsize=0;
	for(int i=0;i<len;i++)
	{
		if(i+nums[i]>maxsize)
		{
			for(int j=maxsize+1;j<=i+nums[i];j++)
			{
				if(j<len)
				{
					time[j]=time[i]+1;
					maxsize=j;		
				}
				else {
					break;
				}
			}
		}
	}
	return time[len-1];
}

还能优化成1ms的就留给你们来了！

结语

原创不易，bigsai请你帮两件事帮忙一下:

1. star支持一下， 您的肯定是我在平台创作的源源动力。

2. 微信搜索「bigsai」，关注我的公众号，不仅免费送你电子书，我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode。

记得关注、咱们下次再见！