LeetCode 51N皇后.md

LeetCode 51N皇后

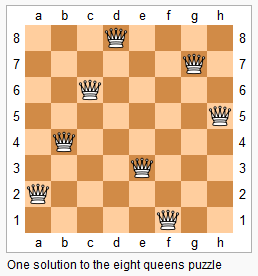
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。 上图为 8 皇后问题的一种解法。 给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。 每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例：

输入：4
输出：[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

提示： 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

八皇后问题我再这篇：回溯算法 | 追忆那些年曾难倒我们的八皇后问题 讲的已经很清楚了，不懂的可以详细看看。

在具体的实现上，就是需要一个map[][]的地图记录各个位置的符号，然后按照规则存储进去，但我这里用了个StringBuilder[]数组来完成。 另外，判断方向的时候因为从一行一行来，如果判断横方向就是多此一举。 附上代码：

// boolean heng[];
 boolean shu[];
 boolean zuoxie[];
 boolean youxie[];

 	 public List<List<String>> solveNQueens(int n) {
	List<List<String>> list=new ArrayList<List<String>>();
	StringBuilder stringBuilder[]=new StringBuilder[n];
	for(int i=0;i<n;i++)
	{
		stringBuilder[i]=new StringBuilder();
		for(int j=0;j<n;j++)
		{
			stringBuilder[i].append('.');
		}
	}
	shu=new boolean[n];
	zuoxie=new boolean[n*2];
	youxie=new boolean[n*2];
	dfs(0,stringBuilder,list,n);
	return list;
 }

private void dfs(int index, StringBuilder sBuilder[], List<List<String>> list,int n) {
	// TODO Auto-generated method stub
	if(index==n)//存入
	{
		List<String>val=new ArrayList<String>();
		//StringBuilder sBuilder=new StringBuilder();
		for(int i=0;i<n;i++)
		{
			val.add(sBuilder[i].toString());
			
		}
		list.add(val);
	}
	else {
		for(int j=0;j<n;j++)
		{
			if(!shu[j]&&!zuoxie[index+j]&&!youxie[index+(n-1-j)])
			{
				shu[j]=true;
				zuoxie[index+j]=true;
				youxie[index+(n-1-j)]=true;
				//map[index][j]='Q';
				sBuilder[index].setCharAt(j, 'Q');
				dfs(index+1,sBuilder, list, n);
				shu[j]=false;
				zuoxie[index+j]=false;
				youxie[index+(n-1-j)]=false;
				sBuilder[index].setCharAt(j, '.');
				//map[index][j]='.';
				
			}
		}
	}	
}

总是熟悉的100%：

结语：好了今天就到这里了，欢迎关注原创技术公众号：【bigsai】，回复进群加笔者微信一起加入打卡！回复「bigsai」，领取进阶资源。