选择排序(Selection Sort)基本思想:
将数组分为两个区间:左侧为已排序区间,右侧为未排序区间。每趟从未排序区间中选择一个值最小的元素,放到已排序区间的末尾,从而将该元素划分到已排序区间。
选择排序是一种简单直观的排序算法,其思想简单,代码也相对容易。
假设数组的元素个数为
- 初始状态下,无已排序区间,未排序区间为
$[0, n - 1]$ 。 - 第
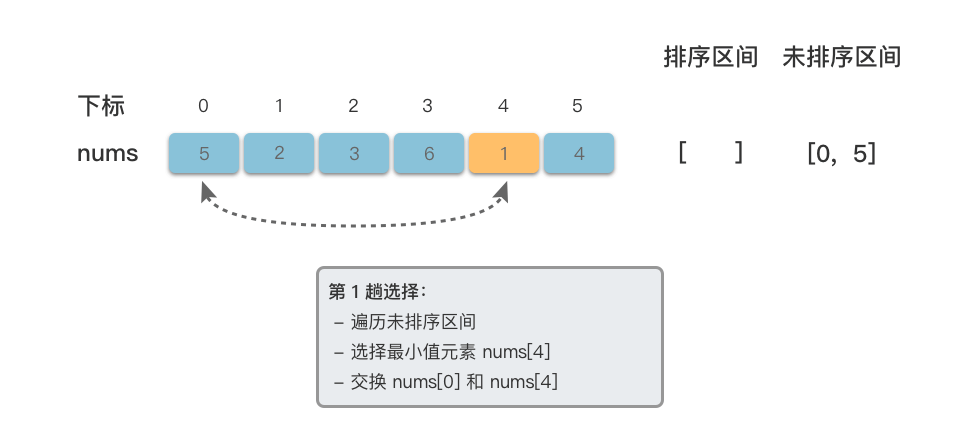
$1$ 趟选择:- 遍历未排序区间
$[0, n - 1]$ ,使用变量$min\underline{}i$ 记录区间中值最小的元素位置。 - 将
$min\underline{}i$ 与下标为$0$ 处的元素交换位置。如果下标为$0$ 处元素就是值最小的元素位置,则不用交换。 - 此时,$[0, 0]$ 为已排序区间,$[1, n - 1]$(总共
$n - 1$ 个元素)为未排序区间。
- 遍历未排序区间
- 第
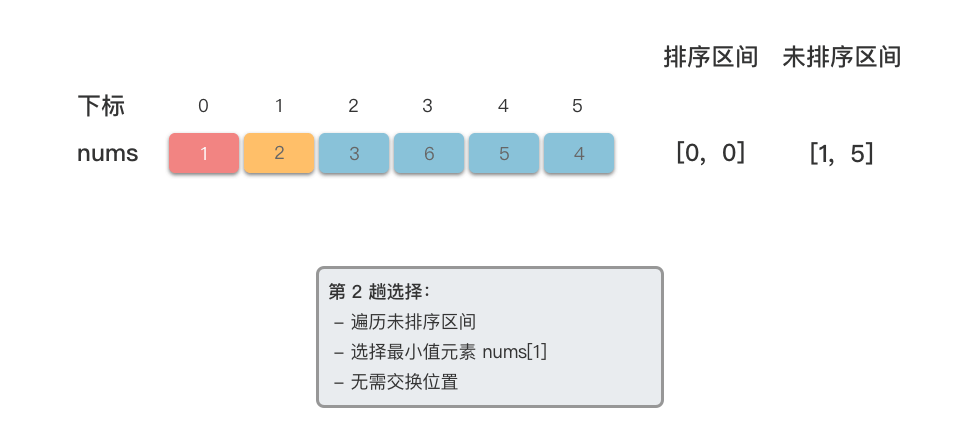
$2$ 趟选择:- 遍历未排序区间
$[1, n - 1]$ ,使用变量$min\underline{}i$ 记录区间中值最小的元素位置。 - 将
$min\underline{}i$ 与下标为$1$ 处的元素交换位置。如果下标为$1$ 处元素就是值最小的元素位置,则不用交换。 - 此时,$[0, 1]$ 为已排序区间,$[2, n - 1]$(总共
$n - 2$ 个元素)为未排序区间。
- 遍历未排序区间
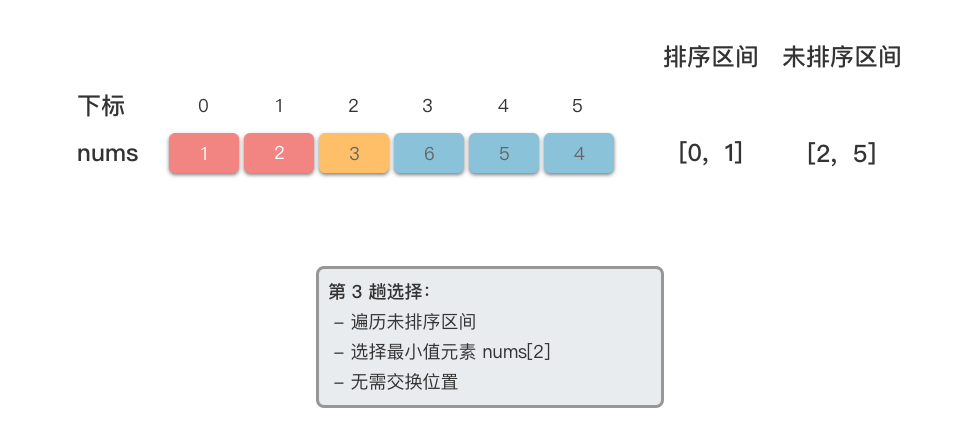
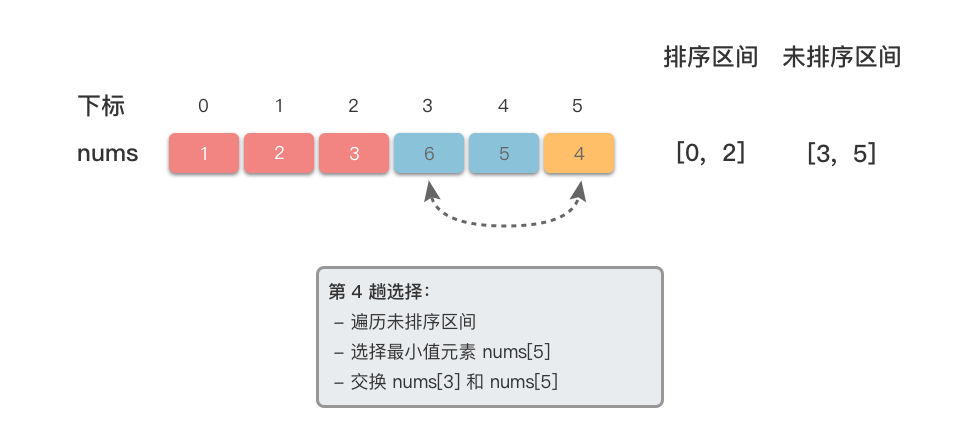
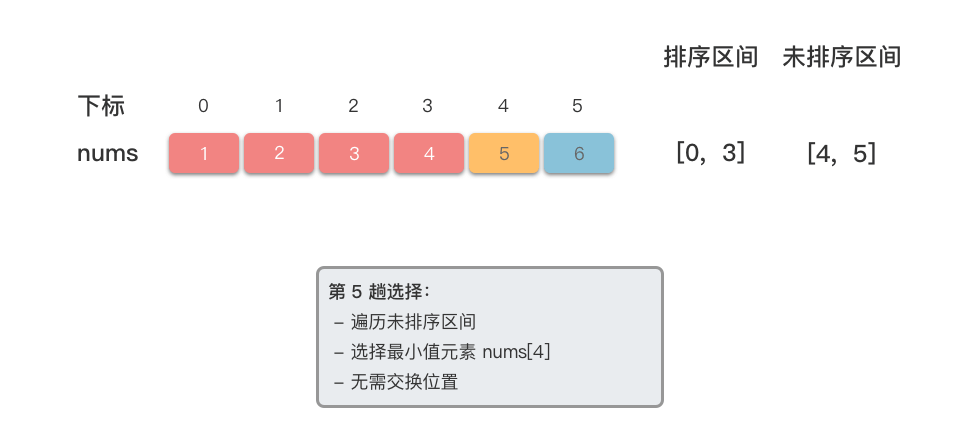
- 依次类推,对剩余未排序区间重复上述选择过程,直到所有元素都划分到已排序区间,排序结束。
我们以
::: tabs#selectionSort
@tab <1>
@tab <2>
@tab <3>
@tab <4>
@tab <5>
@tab <6>
@tab <7>
:::
class Solution:
def selectionSort(self, nums: [int]) -> [int]:
for i in range(len(nums) - 1):
# 记录未排序区间中最小值的位置
min_i = i
for j in range(i + 1, len(nums)):
if nums[j] < nums[min_i]:
min_i = j
# 如果找到最小值的位置,将 i 位置上元素与最小值位置上的元素进行交换
if i != min_i:
nums[i], nums[min_i] = nums[min_i], nums[i]
return nums
def sortArray(self, nums: [int]) -> [int]:
return self.selectionSort(nums)-
时间复杂度:$O(n^2)$。排序法所进行的元素之间的比较次数与序列的原始状态无关,时间复杂度总是
$O(n^2)$ 。- 这是因为无论序列中元素的初始排列状态如何,第
$i$ 趟排序要找出值最小元素都需要进行$n − i$ 次元素之间的比较。因此,整个排序过程需要进行的元素之间的比较次数都相同,为$∑^n_{i=2}(i - 1) = \frac{n(n−1)}{2}$ 次。
- 这是因为无论序列中元素的初始排列状态如何,第
-
空间复杂度:$O(1)$。选择排序算法为原地排序算法,只用到指针变量
$i$ 、$j$ 以及最小值位置$min\underline{}i$ 等常数项的变量。 -
选择排序适用情况:选择排序方法在排序过程中需要移动较多次数的元素,并且排序时间效率比较低。因此,选择排序方法比较适合于参加排序序列的数据量较小的情况。选择排序的主要优点是仅需要原地操作无需占用其他空间就可以完成排序,因此在空间复杂度要求较高时,可以考虑选择排序。
-
排序稳定性:由于值最小元素与未排序区间第
$1$ 个元素的交换动作是在不相邻的元素之间进行的,因此很有可能会改变相等元素的相对顺序,因此,选择排序法是一种 不稳定排序算法。