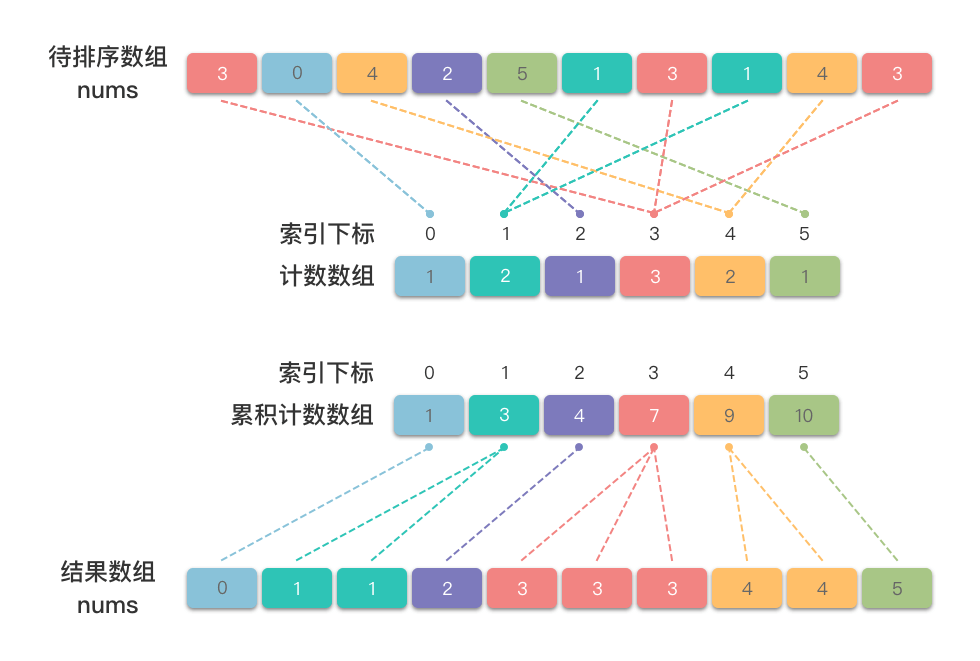
计数排序(Counting Sort)基本思想:
通过统计数组中每个元素在数组中出现的次数,根据这些统计信息将数组元素有序的放置到正确位置,从而达到排序的目的。
-
计算排序范围:遍历数组,找出待排序序列中最大值元素
$nums\underline{}max$ 和最小值元素$nums\underline{}min$ ,计算出排序范围为$nums\underline{}max - nums\underline{}min + 1$ 。 -
定义计数数组:定义一个大小为排序范围的计数数组
$counts$ ,用于统计每个元素的出现次数。其中:- 数组的索引值
$num - nums\underline{}min$ 表示元素的值为$num$ 。 - 数组的值
$counts[num - nums\underline{}min]$ 表示元素$num$ 的出现次数。
- 数组的索引值
-
对数组元素进行计数统计:遍历待排序数组
$nums$ ,对每个元素在计数数组中进行计数,即将待排序数组中「每个元素值减去最小值」作为索引,将「对计数数组中的值」加$1$ ,即令$counts[num - nums\underline{}min]$ 加$1$ 。 -
生成累积计数数组:从
$counts$ 中的第$1$ 个元素开始,每一项累家前一项和。此时$counts[num - nums\underline{}min]$ 表示值为$num$ 的元素在排序数组中最后一次出现的位置。 -
逆序填充目标数组:逆序遍历数组
$nums$ ,将每个元素$num$ 填入正确位置。 -
将其填充到结果数组
$res$ 的索引$counts[num - nums\underline{}min]$ 处。 -
放入后,令累积计数数组中对应索引减
$1$ ,从而得到下个元素$num$ 的放置位置。
我们以
class Solution:
def countingSort(self, nums: [int]) -> [int]:
# 计算待排序数组中最大值元素 nums_max 和最小值元素 nums_min
nums_min, nums_max = min(nums), max(nums)
# 定义计数数组 counts,大小为 最大值元素 - 最小值元素 + 1
size = nums_max - nums_min + 1
counts = [0 for _ in range(size)]
# 统计值为 num 的元素出现的次数
for num in nums:
counts[num - nums_min] += 1
# 生成累积计数数组
for i in range(1, size):
counts[i] += counts[i - 1]
# 反向填充目标数组
res = [0 for _ in range(len(nums))]
for i in range(len(nums) - 1, -1, -1):
num = nums[i]
# 根据累积计数数组,将 num 放在数组对应位置
res[counts[num - nums_min] - 1] = num
# 将 num 的对应放置位置减 1,从而得到下个元素 num 的放置位置
counts[nums[i] - nums_min] -= 1
return res
def sortArray(self, nums: [int]) -> [int]:
return self.countingSort(nums)-
时间复杂度:$O(n + k)$。其中
$k$ 代表待排序数组的值域。 -
空间复杂度:$O(k)$。其中
$k$ 代表待排序序列的值域。由于用于计数的数组$counts$ 的长度取决于待排序数组中数据的范围(大小等于待排序数组最大值减去最小值再加$1$ )。所以计数排序算法对于数据范围很大的数组,需要大量的内存。 - 计数排序适用情况:计数排序一般用于整数排序,不适用于按字母顺序、人名顺序排序。
- 排序稳定性:由于向结果数组中填充元素时使用的是逆序遍历,可以避免改变相等元素之间的相对顺序。因此,计数排序是一种 稳定排序算法。