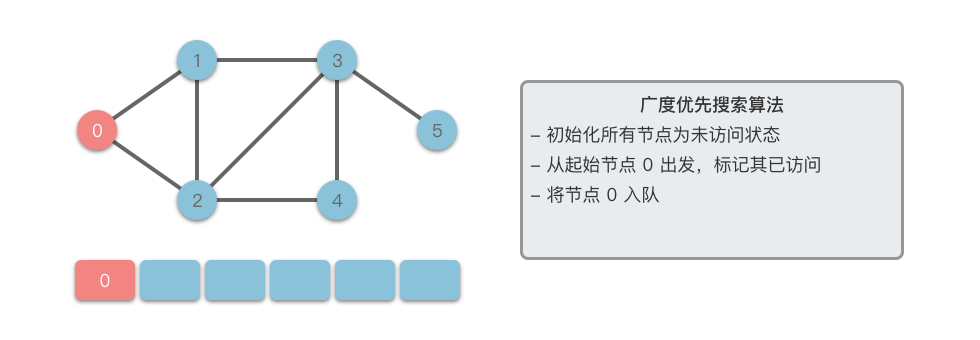
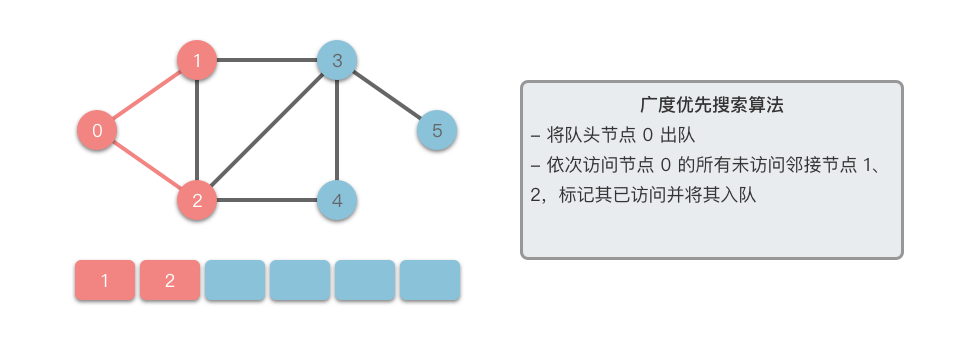
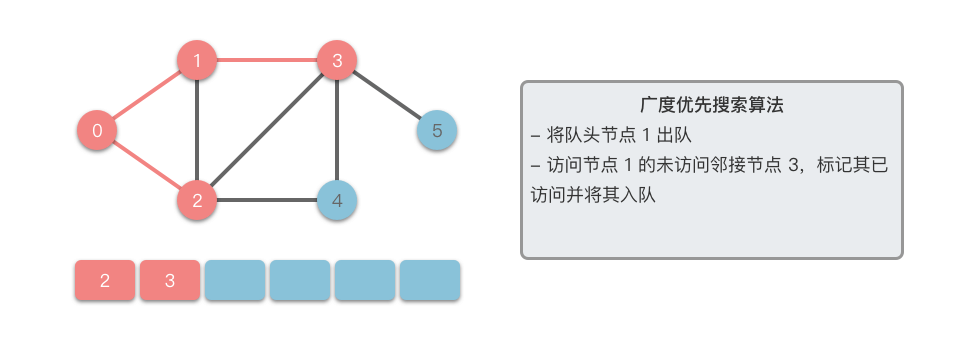
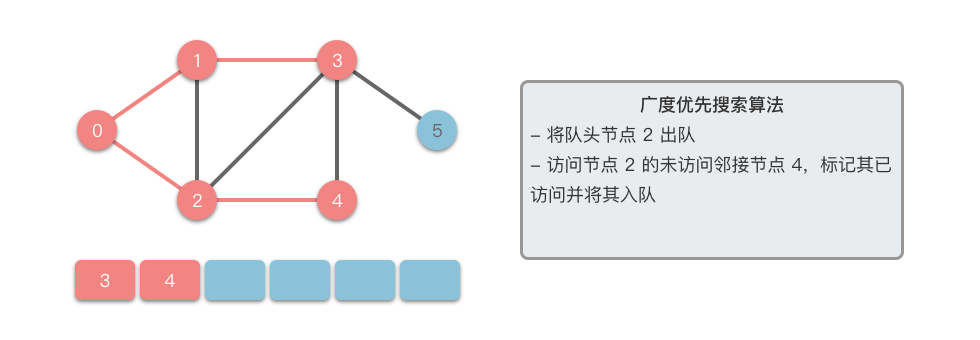
广度优先搜索算法(Breadth First Search):英文缩写为 BFS,又译作宽度优先搜索 / 横向优先搜索,是一种用于搜索树或图结构的算法。广度优先搜索算法从起始节点开始,逐层扩展,先访问离起始节点最近的节点,后访问离起始节点稍远的节点。以此类推,直到完成整个搜索过程。
因为遍历到的节点顺序符合「先进先出」的特点,所以广度优先搜索可以通过「队列」来实现。
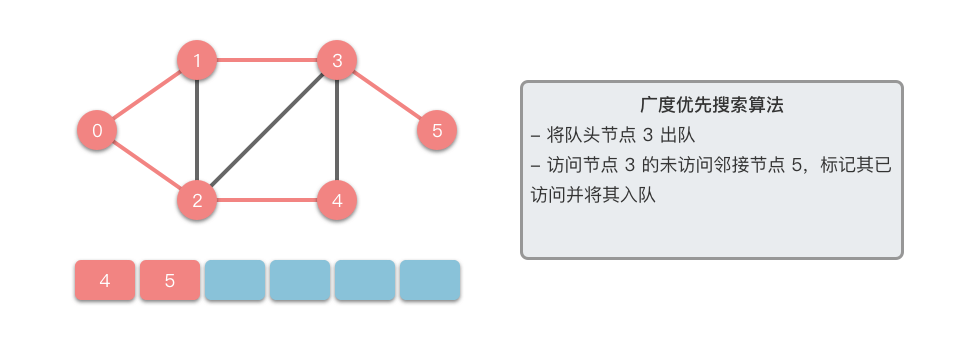
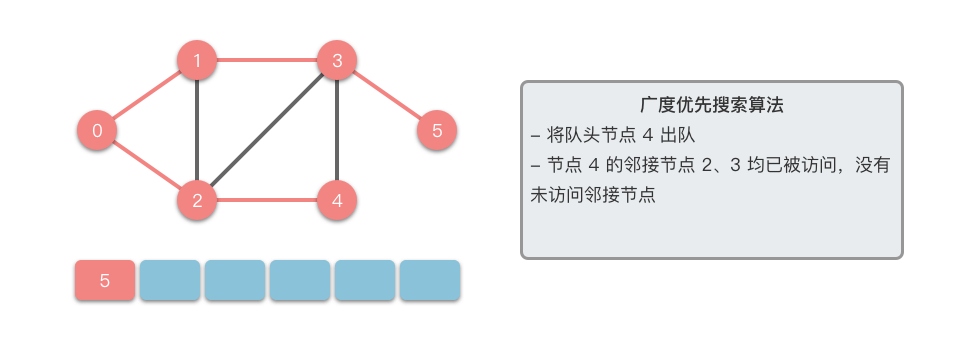
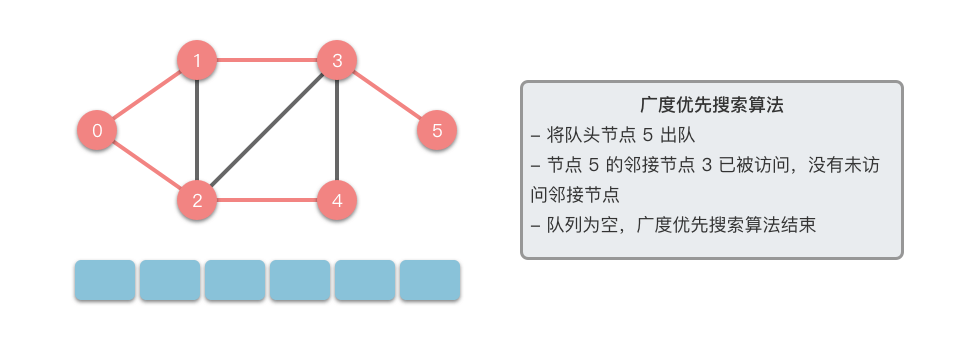
接下来我们以一个无向图为例,介绍一下广度优先搜索的算法步骤。
- 将起始节点
$u$ 放入队列中,并标记为已访问。 - 从队列中取出一个节点,访问它并将其所有的未访问邻接节点
$v$ 放入队列中。 - 标记已访问的节点
$v$ ,以避免重复访问。 - 重复步骤
$2 \sim 3$ ,直到队列为空或找到目标节点。
::: tabs#BFS
@tab <1>
@tab <2>
@tab <3>
@tab <4>
@tab <5>
@tab <6>
@tab <7>
:::
- 定义
$graph$ 为存储无向图的嵌套数组变量,$visited$ 为标记访问节点的集合变量,$queue$ 为存放节点的队列,$u$ 为开始节点,定义def bfs(graph, u):为队列实现的广度优先搜索方法。 - 首先将起始节点
$u$ 标记为已访问,并将其加入队列中,即visited.add(u),queue.append(u)。 - 从队列中取出队头节点
$u$ 。访问节点$u$ ,并对节点进行相关操作(看具体题目要求)。 - 遍历节点
$u$ 的所有未访问邻接节点$v$ (节点$v$ 不在$visited$ 中)。 - 将节点
$v$ 标记已访问,并加入队列中,即visited.add(v),queue.append(v)。 - 重复步骤
$3 \sim 5$ ,直到队列$queue$ 为空。
import collections
class Solution:
def bfs(self, graph, u):
visited = set() # 使用 visited 标记访问过的节点
queue = collections.deque([]) # 使用 queue 存放临时节点
visited.add(u) # 将起始节点 u 标记为已访问
queue.append(u) # 将起始节点 u 加入队列中
while queue: # 队列不为空
u = queue.popleft() # 取出队头节点 u
print(u) # 访问节点 u
for v in graph[u]: # 遍历节点 u 的所有未访问邻接节点 v
if v not in visited: # 节点 v 未被访问
visited.add(v) # 将节点 v 标记为已访问
queue.append(v) # 将节点 v 加入队列中
graph = {
"0": ["1", "2"],
"1": ["0", "2", "3"],
"2": ["0", "1", "3", "4"],
"3": ["1", "2", "4", "5"],
"4": ["2", "3"],
"5": ["3", "6"],
"6": []
}
# 基于队列实现的广度优先搜索
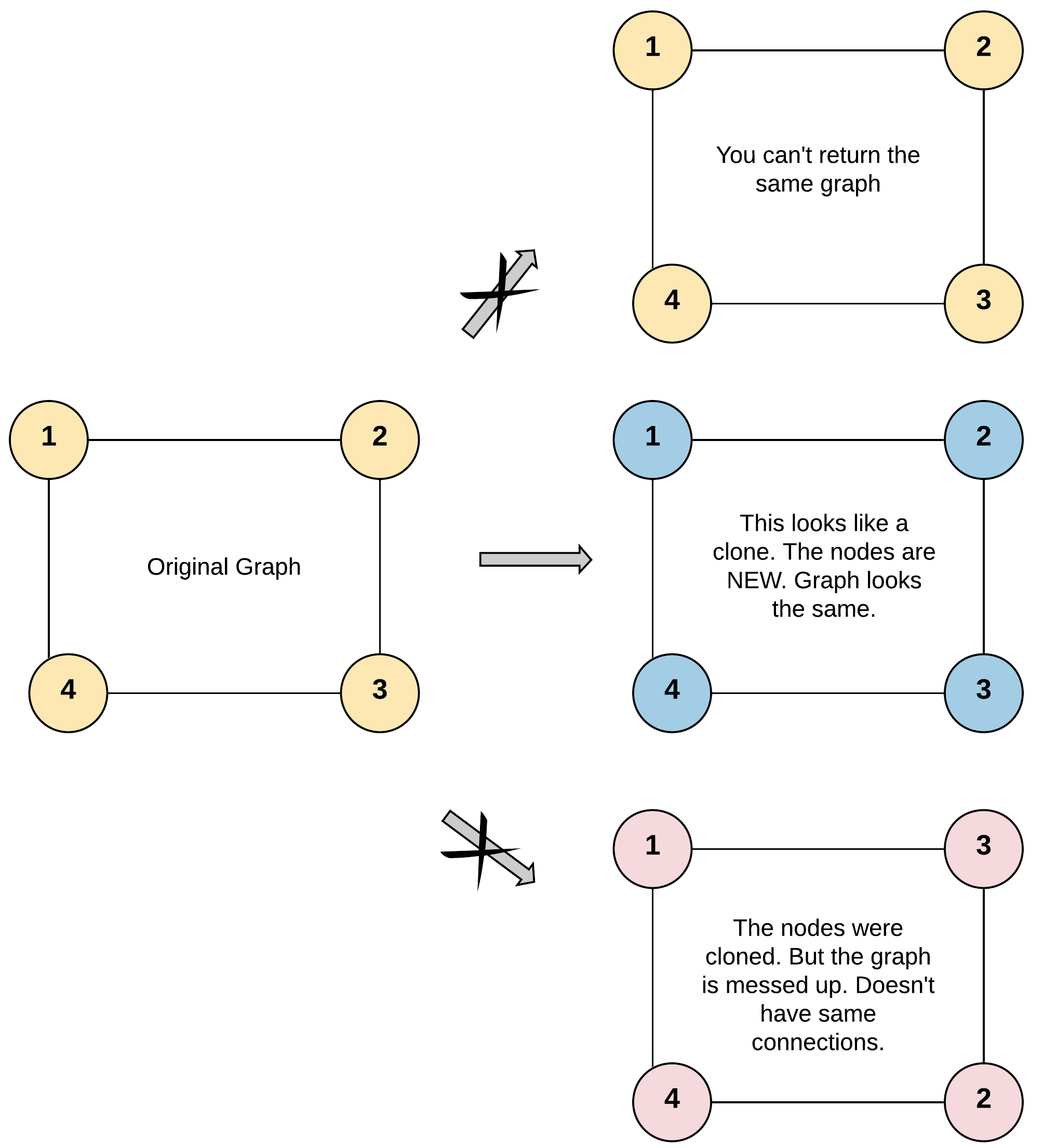
Solution().bfs(graph, "0")描述:以每个节点的邻接列表形式(二维列表)给定一个无向连通图,其中
要求:返回该图的深拷贝。
说明:
- 节点数不超过
$100$ 。 - 每个节点值
$Node.val$ 都是唯一的,$1 \le Node.val \le 100$。 - 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点
$p$ 是节点$q$ 的邻居,那么节点$q$ 也必须是节点$p$ 的邻居。 - 图是连通图,你可以从给定节点访问到所有节点。
示例:
- 示例 1:
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。- 示例 2:
输入:adjList = [[2],[1]]
输出:[[2],[1]]- 使用哈希表
$visited$ 来存储原图中被访问过的节点和克隆图中对应节点,键值对为「原图被访问过的节点:克隆图中对应节点」。使用队列$queue$ 存放节点。 - 根据起始节点
$node$ ,创建一个新的节点,并将其添加到哈希表$visited$ 中,即visited[node] = Node(node.val, [])。然后将起始节点放入队列中,即queue.append(node)。 - 从队列中取出第一个节点
$node\underline{}u$ 。访问节点$node\underline{}u$ 。 - 遍历节点
$node\underline{}u$ 的所有未访问邻接节点$node\underline{}v$ (节点$node\underline{}v$ 不在$visited$ 中)。 - 根据节点
$node\underline{}v$ 创建一个新的节点,并将其添加到哈希表$visited$ 中,即visited[node_v] = Node(node_v.val, [])。 - 然后将节点
$node\underline{}v$ 放入队列$queue$ 中,即queue.append(node_v)。 - 重复步骤
$3 \sim 6$ ,直到队列$queue$ 为空。 - 广度优先搜索结束,返回起始节点的克隆节点(即
$visited[node]$ )。
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node:
return node
visited = dict()
queue = collections.deque()
visited[node] = Node(node.val, [])
queue.append(node)
while queue:
node_u = queue.popleft()
for node_v in node_u.neighbors:
if node_v not in visited:
visited[node_v] = Node(node_v.val, [])
queue.append(node_v)
visited[node_u].neighbors.append(visited[node_v])
return visited[node]-
时间复杂度:$O(n)$。其中
$n$ 为图中节点数量。 - 空间复杂度:$O(n)$。
描述:给定一个只包含
要求:计算出最大的岛屿面积。
说明:
-
$m == grid.length$ 。 -
$n == grid[i].length$ 。 -
$1 \le m, n \le 50$ 。 -
$grid[i][j]$ 为$0$ 或$1$ 。
示例:
- 示例 1:
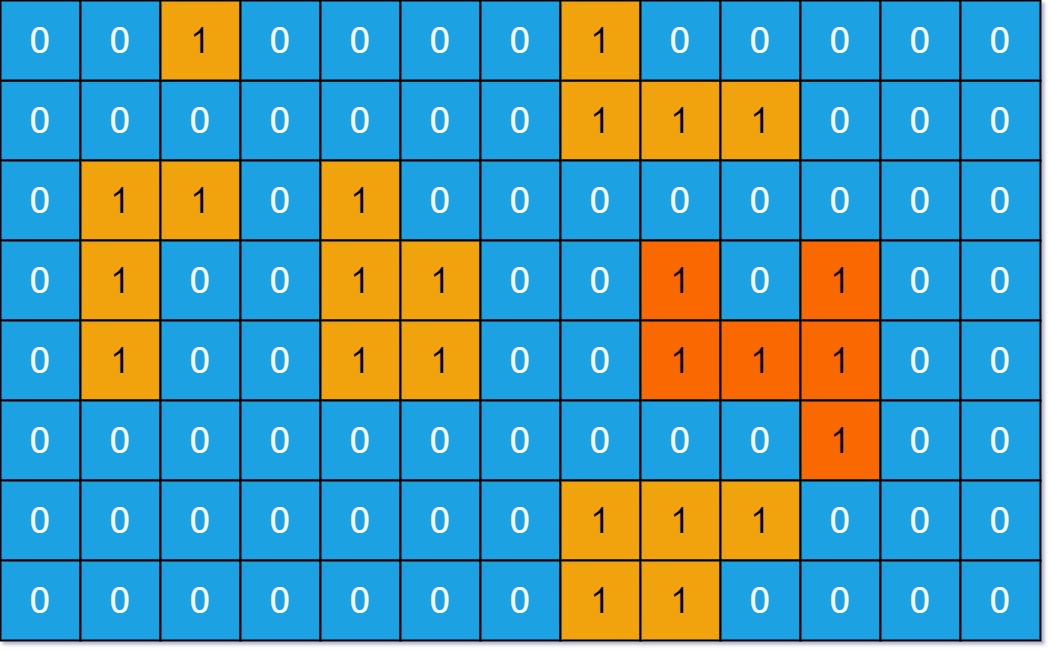
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。- 示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0- 使用
$ans$ 记录最大岛屿面积。 - 遍历二维数组的每一个元素,对于每个值为
$1$ 的元素:- 将该元素置为
$0$ 。并使用队列$queue$ 存储该节点位置。使用$temp\underline{}ans$ 记录当前岛屿面积。 - 然后从队列
$queue$ 中取出第一个节点位置$(i, j)$ 。遍历该节点位置上、下、左、右四个方向上的相邻节点。并将其置为$0$ (避免重复搜索)。并将其加入到队列中。并累加当前岛屿面积,即temp_ans += 1。 - 不断重复上一步骤,直到队列
$queue$ 为空。 - 更新当前最大岛屿面积,即
ans = max(ans, temp_ans)。
- 将该元素置为
- 将
$ans$ 作为答案返回。
import collections
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
directs = [(0, 1), (0, -1), (1, 0), (-1, 0)]
rows, cols = len(grid), len(grid[0])
ans = 0
for i in range(rows):
for j in range(cols):
if grid[i][j] == 1:
grid[i][j] = 0
temp_ans = 1
queue = collections.deque([(i, j)])
while queue:
i, j = queue.popleft()
for direct in directs:
new_i = i + direct[0]
new_j = j + direct[1]
if new_i < 0 or new_i >= rows or new_j < 0 or new_j >= cols or grid[new_i][new_j] == 0:
continue
grid[new_i][new_j] = 0
queue.append((new_i, new_j))
temp_ans += 1
ans = max(ans, temp_ans)
return ans-
时间复杂度:$O(n \times m)$,其中
$m$ 和$n$ 分别为行数和列数。 - 空间复杂度:$O(n \times m)$。