Given n points on a 2D plane, find if there is such a line parallel to the y-axis that reflects the given points symmetrically.
In other words, answer whether or not if there exists a line that after reflecting all points over the given line, the original points' set is the same as the reflected ones.
Note that there can be repeated points.
Example 1:
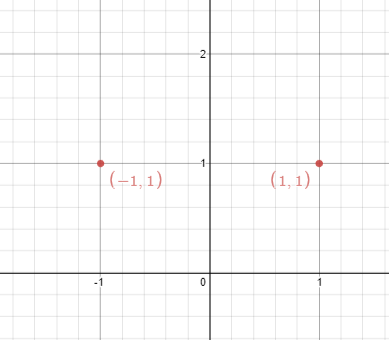
Input: points = [[1,1],[-1,1]] Output: true Explanation: We can choose the line x = 0.
Example 2:
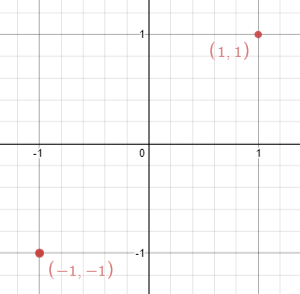
Input: points = [[1,1],[-1,-1]] Output: false Explanation: We can't choose a line.
Constraints:
n == points.length1 <= n <= 104-108 <= points[i][j] <= 108
Follow up: Could you do better than O(n2)?
class Solution:
def isReflected(self, points: List[List[int]]) -> bool:
min_x, max_x = inf, -inf
point_set = set()
for x, y in points:
min_x = min(min_x, x)
max_x = max(max_x, x)
point_set.add((x, y))
s = min_x + max_x
for x, y in points:
if (s - x, y) not in point_set:
return False
return Trueclass Solution {
public boolean isReflected(int[][] points) {
int minX = Integer.MAX_VALUE, maxX = Integer.MIN_VALUE;
Set<String> pointSet = new HashSet<>();
for (int[] point : points) {
minX = Math.min(minX, point[0]);
maxX = Math.max(maxX, point[0]);
pointSet.add(point[0] + "." + point[1]);
}
long s = minX + maxX;
for (int[] point : points) {
if (!pointSet.contains((s - point[0]) + "." + point[1])) {
return false;
}
}
return true;
}
}