Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.
Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
Example 1:
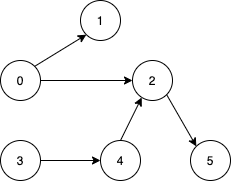
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]] Output: [0,3] Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].
Example 2:
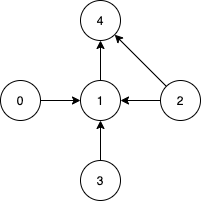
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]] Output: [0,2,3] Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
Constraints:
<li><code>2 <= n <= 10^5</code></li>
<li><code>1 <= edges.length <= min(10^5, n * (n - 1) / 2)</code></li>
<li><code>edges[i].length == 2</code></li>
<li><code>0 <= from<sub>i,</sub> to<sub>i</sub> < n</code></li>
<li>All pairs <code>(from<sub>i</sub>, to<sub>i</sub>)</code> are distinct.</li>
class Solution:
def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:
s = {to for _, to in edges}
return [i for i in range(n) if i not in s]class Solution {
public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
Set<Integer> s = new HashSet<>();
for (List<Integer> e : edges) {
s.add(e.get(1));
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < n; ++i) {
if (!s.contains(i)) {
ans.add(i);
}
}
return ans;
}
}class Solution {
public:
vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {
unordered_set<int> s;
for (auto& e : edges) s.insert(e[1]);
vector<int> ans;
for (int i = 0; i < n; ++i) {
if (!s.count(i)) ans.push_back(i);
}
return ans;
}
};func findSmallestSetOfVertices(n int, edges [][]int) []int {
s := make(map[int]bool)
for _, e := range edges {
s[e[1]] = true
}
var ans []int
for i := 0; i < n; i++ {
if !s[i] {
ans = append(ans, i)
}
}
return ans
}function findSmallestSetOfVertices(n: number, edges: number[][]): number[] {
const arr = new Array(n).fill(true);
for (const [_, i] of edges) {
arr[i] = false;
}
const res = [];
arr.forEach((v, i) => {
if (v) {
res.push(i);
}
});
return res;
}impl Solution {
pub fn find_smallest_set_of_vertices(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {
let mut arr = vec![true; n as usize];
edges.iter().for_each(|edge| {
arr[edge[1] as usize] = false;
});
arr.iter()
.enumerate()
.filter_map(|(i, &v)| if v { Some(i as i32) } else { None })
.collect()
}
}