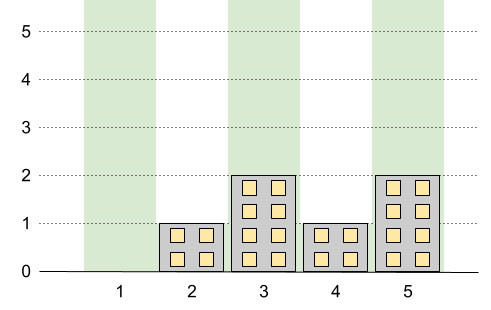在一座城市里,你需要建 n 栋新的建筑。这些新的建筑会从 1 到 n 编号排成一列。
这座城市对这些新建筑有一些规定:
- 每栋建筑的高度必须是一个非负整数。
- 第一栋建筑的高度 必须 是
0。 - 任意两栋相邻建筑的高度差 不能超过
1。
除此以外,某些建筑还有额外的最高高度限制。这些限制会以二维整数数组 restrictions 的形式给出,其中 restrictions[i] = [idi, maxHeighti] ,表示建筑 idi 的高度 不能超过 maxHeighti 。
题目保证每栋建筑在 restrictions 中 至多出现一次 ,同时建筑 1 不会 出现在 restrictions 中。
请你返回 最高 建筑能达到的 最高高度 。
示例 1:
输入:n = 5, restrictions = [[2,1],[4,1]] 输出:2 解释:上图中的绿色区域为每栋建筑被允许的最高高度。 我们可以使建筑高度分别为 [0,1,2,1,2] ,最高建筑的高度为 2 。
示例 2:
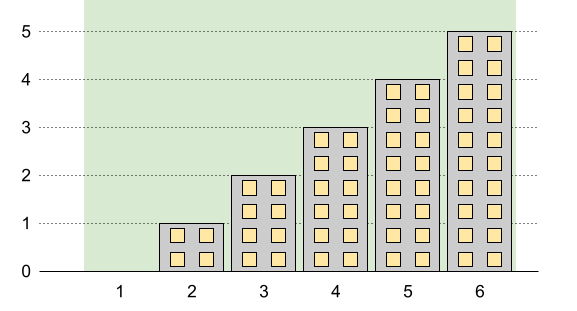
输入:n = 6, restrictions = [] 输出:5 解释:上图中的绿色区域为每栋建筑被允许的最高高度。 我们可以使建筑高度分别为 [0,1,2,3,4,5] ,最高建筑的高度为 5 。
示例 3:
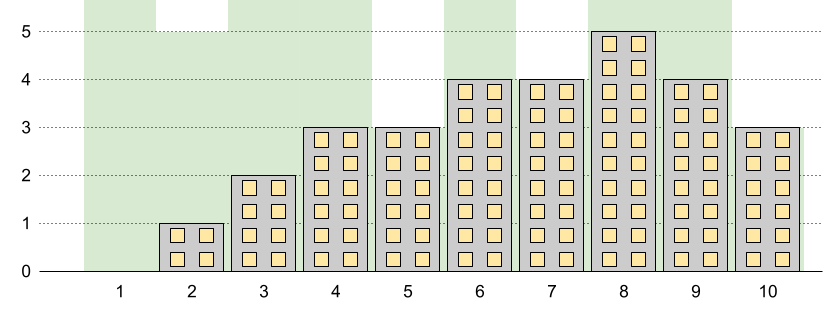
输入:n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]] 输出:5 解释:上图中的绿色区域为每栋建筑被允许的最高高度。 我们可以使建筑高度分别为 [0,1,2,3,3,4,4,5,4,3] ,最高建筑的高度为 5 。
提示:
2 <= n <= 1090 <= restrictions.length <= min(n - 1, 105)2 <= idi <= nidi是 唯一的 。0 <= maxHeighti <= 109
方法一:排序 + 数学
首先,我们将所有的限制条件按照建筑物的编号从小到大排序。
然后我们从左到右遍历所有的限制条件,对于每个限制条件,我们可以得到一个最高高度的上界,即
然后我们从右到左遍历所有的限制条件,对于每个限制条件,我们可以得到一个最高高度的上界,即
这样,我们就得到了每个限制建筑物的最高高度的上界。
题目求的是最高建筑物的高度,我们可以枚举相邻两个限制条件之间的建筑物
时间复杂度
class Solution:
def maxBuilding(self, n: int, restrictions: List[List[int]]) -> int:
r = restrictions
r.append([1, 0])
r.sort()
if r[-1][0] != n:
r.append([n, n - 1])
m = len(r)
for i in range(1, m):
r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0])
for i in range(m - 2, 0, -1):
r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0])
ans = 0
for i in range(m - 1):
t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) // 2
ans = max(ans, t)
return ansclass Solution {
public int maxBuilding(int n, int[][] restrictions) {
List<int[]> r = new ArrayList<>();
r.addAll(Arrays.asList(restrictions));
r.add(new int[] {1, 0});
Collections.sort(r, (a, b) -> a[0] - b[0]);
if (r.get(r.size() - 1)[0] != n) {
r.add(new int[] {n, n - 1});
}
int m = r.size();
for (int i = 1; i < m; ++i) {
int[] a = r.get(i - 1), b = r.get(i);
b[1] = Math.min(b[1], a[1] + b[0] - a[0]);
}
for (int i = m - 2; i > 0; --i) {
int[] a = r.get(i), b = r.get(i + 1);
a[1] = Math.min(a[1], b[1] + b[0] - a[0]);
}
int ans = 0;
for (int i = 0; i < m - 1; ++i) {
int[] a = r.get(i), b = r.get(i + 1);
int t = (a[1] + b[1] + b[0] - a[0]) / 2;
ans = Math.max(ans, t);
}
return ans;
}
}class Solution {
public:
int maxBuilding(int n, vector<vector<int>>& restrictions) {
auto&& r = restrictions;
r.push_back({1, 0});
sort(r.begin(), r.end());
if (r[r.size() - 1][0] != n) r.push_back({n, n - 1});
int m = r.size();
for (int i = 1; i < m; ++i) {
r[i][1] = min(r[i][1], r[i - 1][1] + r[i][0] - r[i - 1][0]);
}
for (int i = m - 2; i > 0; --i) {
r[i][1] = min(r[i][1], r[i + 1][1] + r[i + 1][0] - r[i][0]);
}
int ans = 0;
for (int i = 0; i < m - 1; ++i) {
int t = (r[i][1] + r[i + 1][1] + r[i + 1][0] - r[i][0]) / 2;
ans = max(ans, t);
}
return ans;
}
};func maxBuilding(n int, restrictions [][]int) (ans int) {
r := restrictions
r = append(r, []int{1, 0})
sort.Slice(r, func(i, j int) bool { return r[i][0] < r[j][0] })
if r[len(r)-1][0] != n {
r = append(r, []int{n, n - 1})
}
m := len(r)
for i := 1; i < m; i++ {
r[i][1] = min(r[i][1], r[i-1][1]+r[i][0]-r[i-1][0])
}
for i := m - 2; i > 0; i-- {
r[i][1] = min(r[i][1], r[i+1][1]+r[i+1][0]-r[i][0])
}
for i := 0; i < m-1; i++ {
t := (r[i][1] + r[i+1][1] + r[i+1][0] - r[i][0]) / 2
ans = max(ans, t)
}
return ans
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}