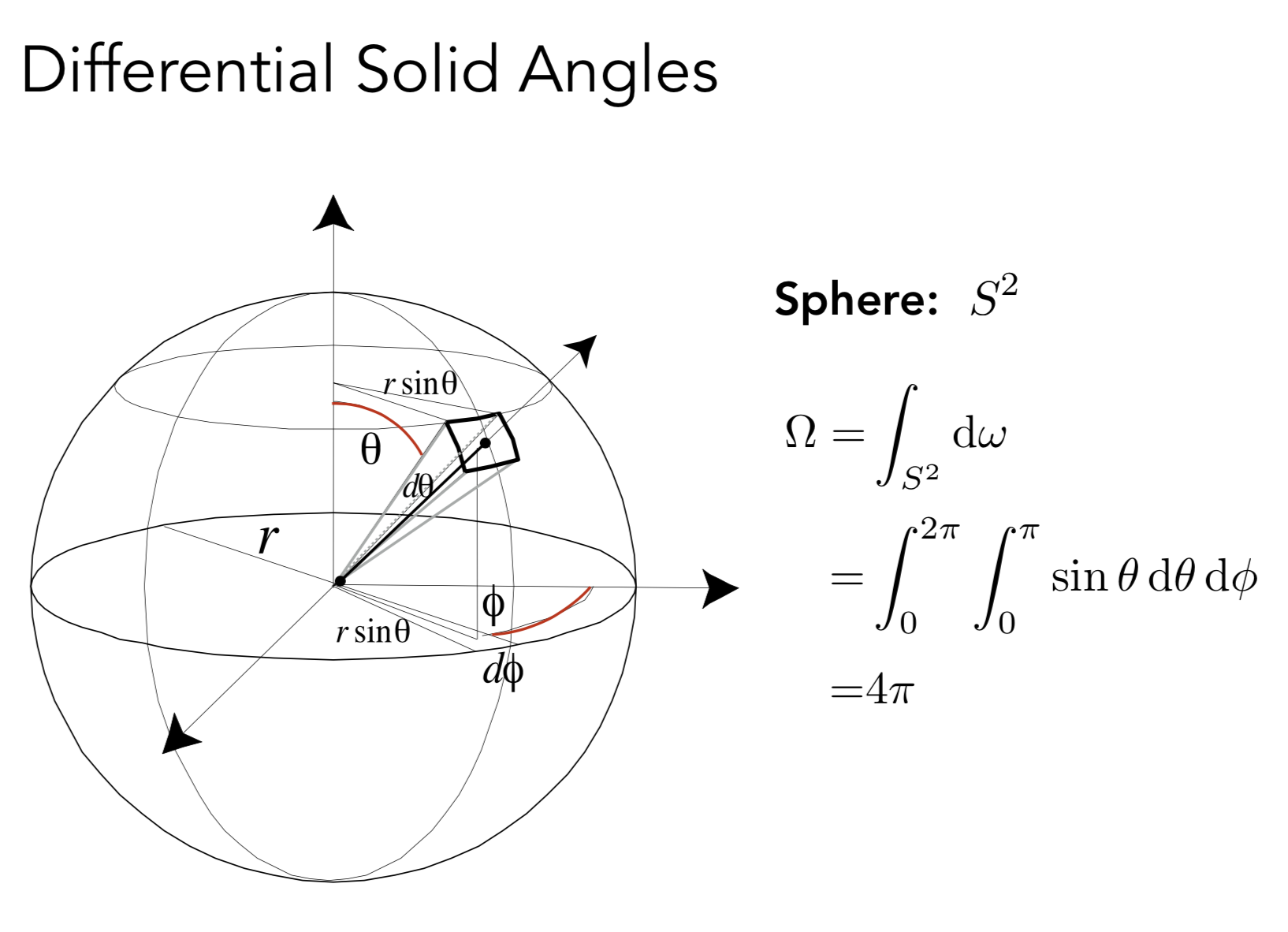
是一个极小的立体角
θ是和 Y轴的夹角, φ 是围绕 y 的旋转角度
PS 注意公式中的 sinθ 微分立体角 和 θ 有关, 靠近赤道和极地变化率不一样
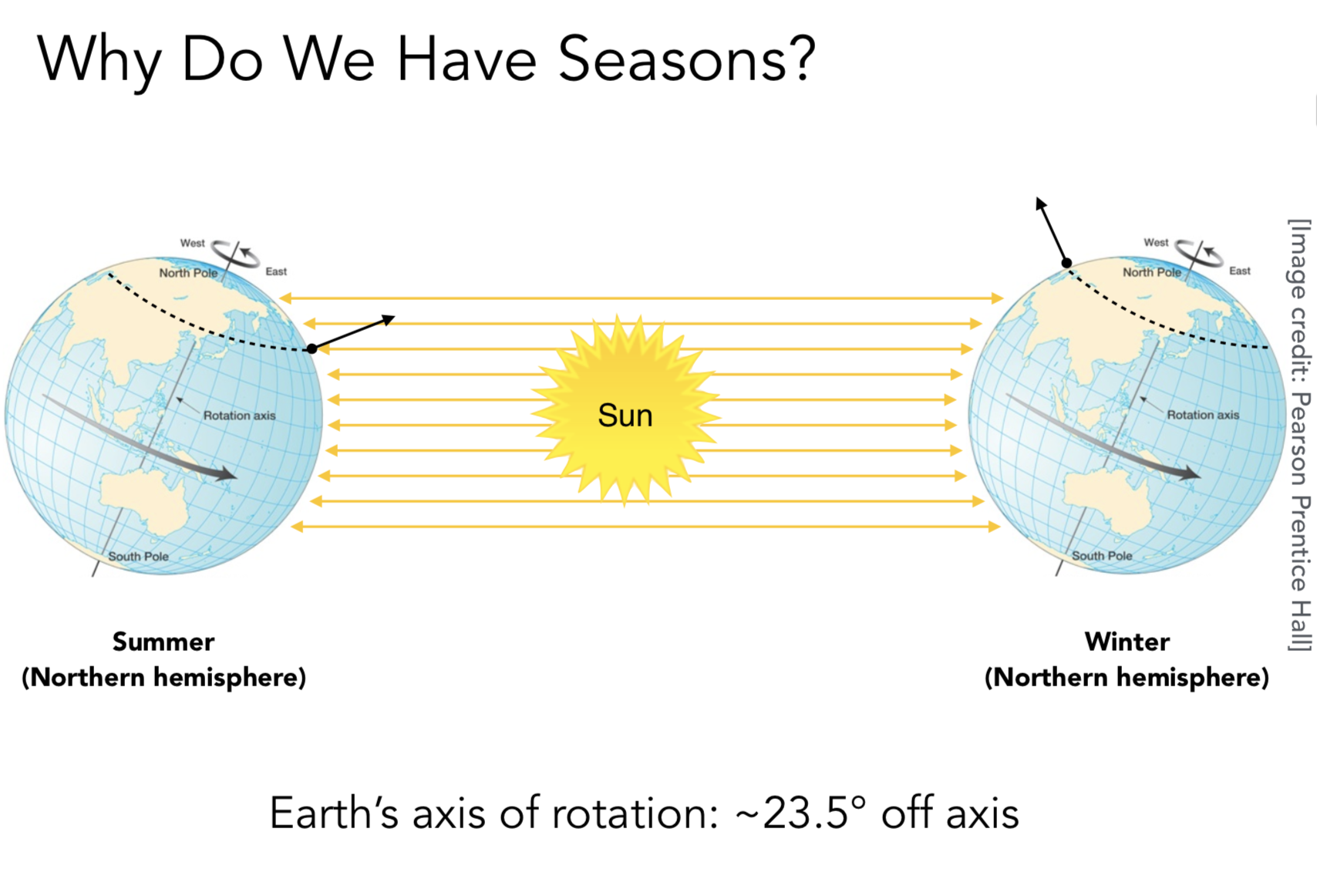
一个物体表面单位面积接收到的光的能量
四季: 阳光和表面越垂直 接收到的能量就越多
能量总和是固定的
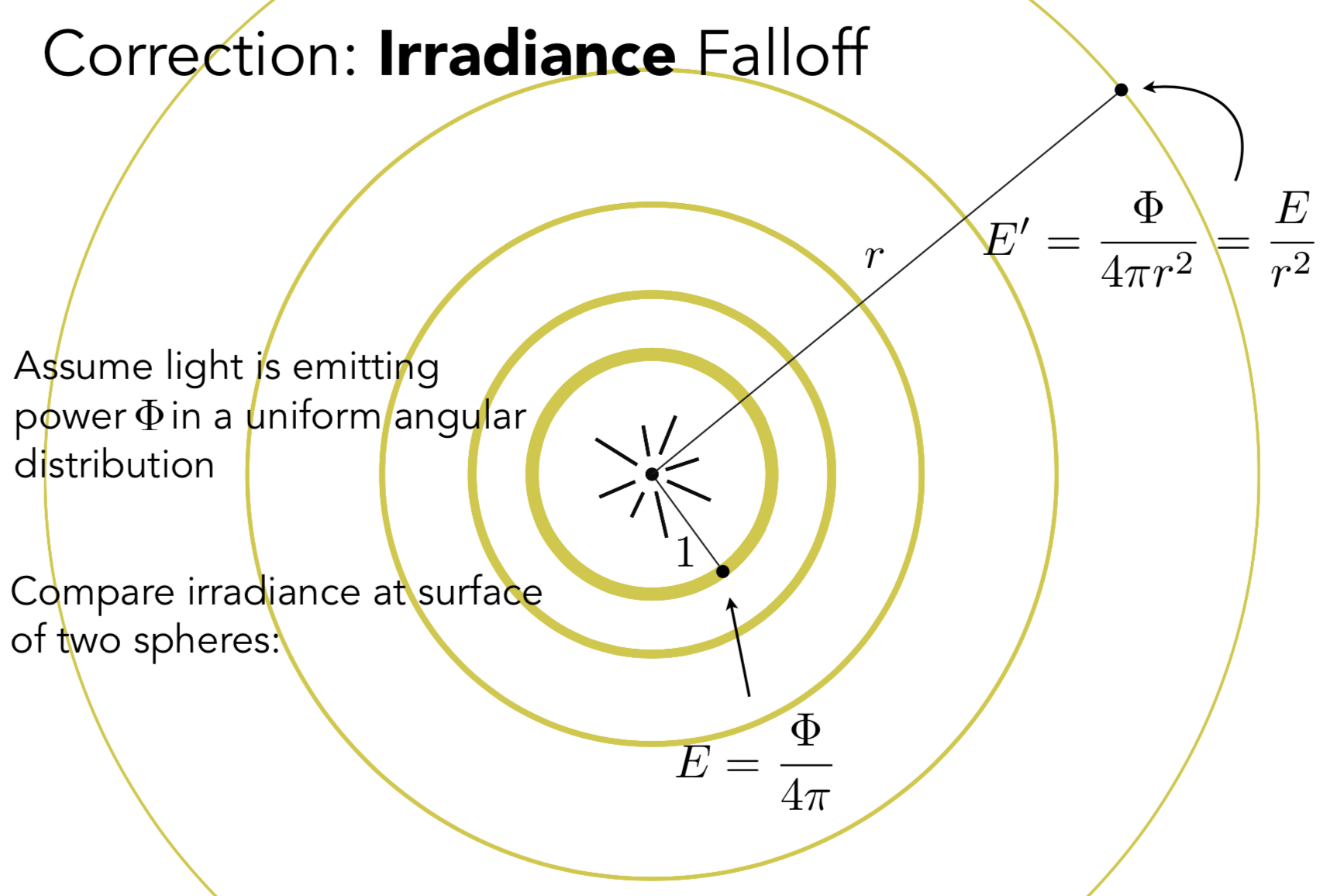
注意intensity 没有变 (Radiant Intensity 是单位立体角上的power 随着 r 变大, 立体角并没有改变 )
是 Irrediance 在随着 r 变大在衰减 (因为壳越来越大了 表面积也变大了 而Irrediance是单位面积上的能量)
power per solid angle, per project unit area 其中 power per solid angle 就是辐射强度 Radiant intensity
Irradiance 是四面八方各个能量的辐射
Radiance 其实是在 Irradiance 基础上增加了方向
Radiance 总体来说就是一个很小的面和一个很小的范围(单一方向)
dA 的能量就是每一个从每个方向来的的能量做积分. 或者说 Irradiance 就是是四面八方的 Radiance 的积分(求和)
用于描述了光线和物体如何相互作用 或者说是BRDF 定义了材质
通俗的说, BRDF是在解决光从某个方向打到以个物体上, 光向反射到不同方向的能量分布. OR 对于一个物体的表面, 如何把收集到的能量反射的另外的方向上去.
对于反射的理解:
Whitted Style 光线打到某一个物体上, 然后被弹走了(方向改变了).
另一种理解: 光线打到某一个表面, 被吸收了, 然后从这个物体表面, 朝某个特定的方向发射出去.
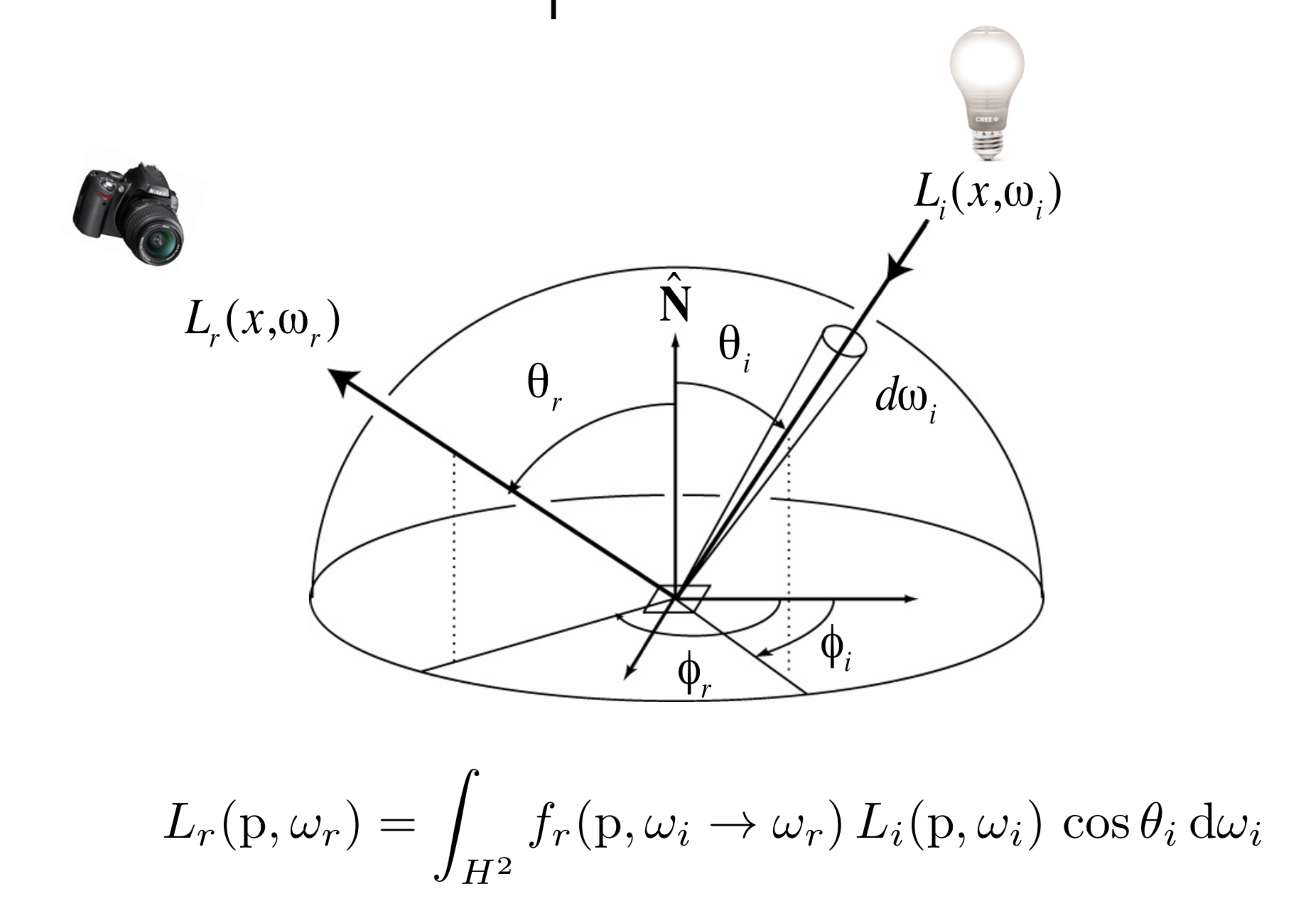
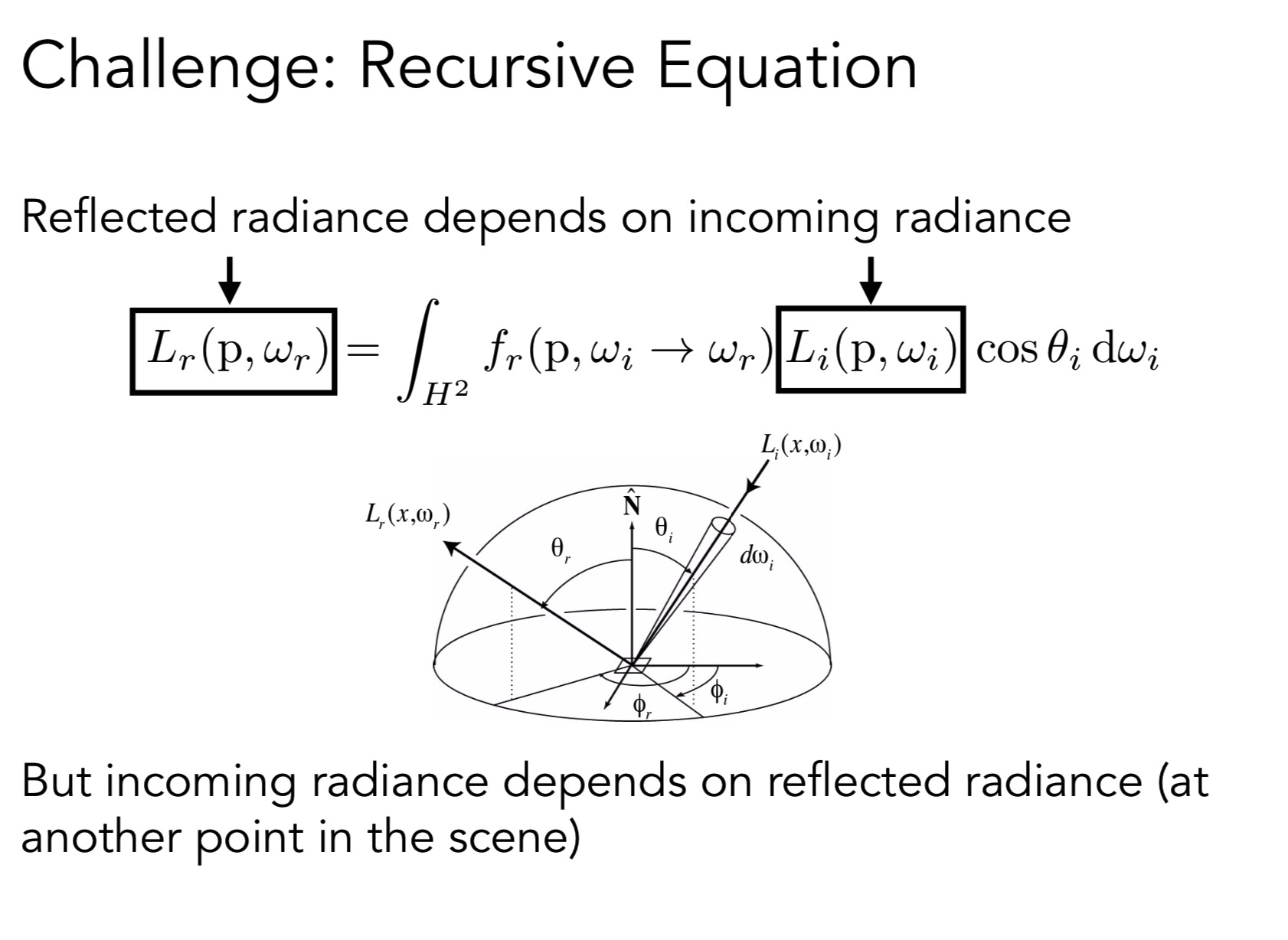
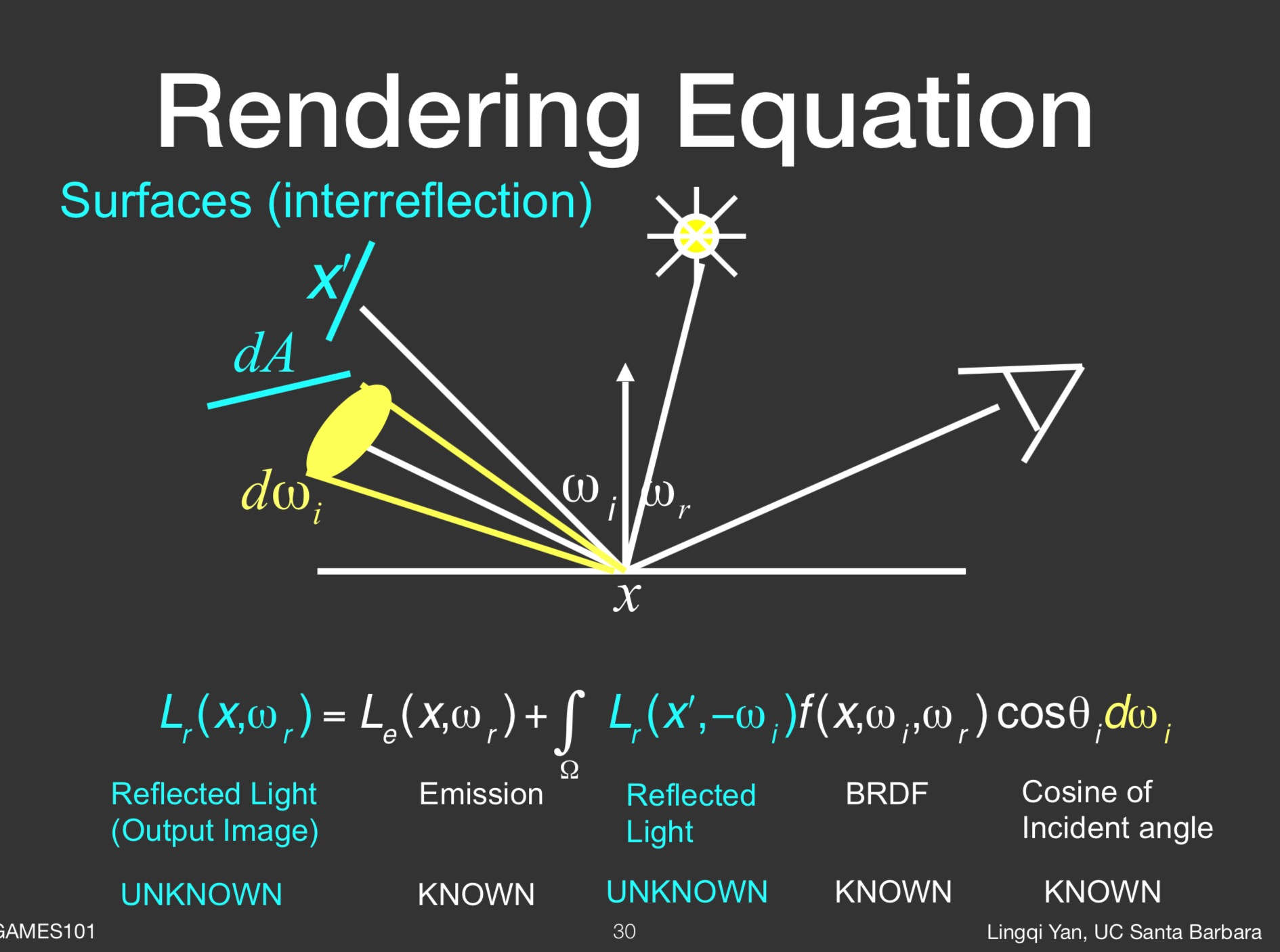
PS: Li(p, ωi)cos(θi)dωi 是图中那一个小块区域dA得到的 Irradiance 其中Li(p, ωi)是入射能量
PS: 然后乘以BRDF 函数fr(p, ωi -> wr) 就得到出射的Radiace, 最后整体做积分
PS: 这里的H 表示半球面
关于此渲染方程 Read More https://zh.wikipedia.org/wiki/%E6%B8%B2%E6%9F%93%E6%96%B9%E7%A8%8B
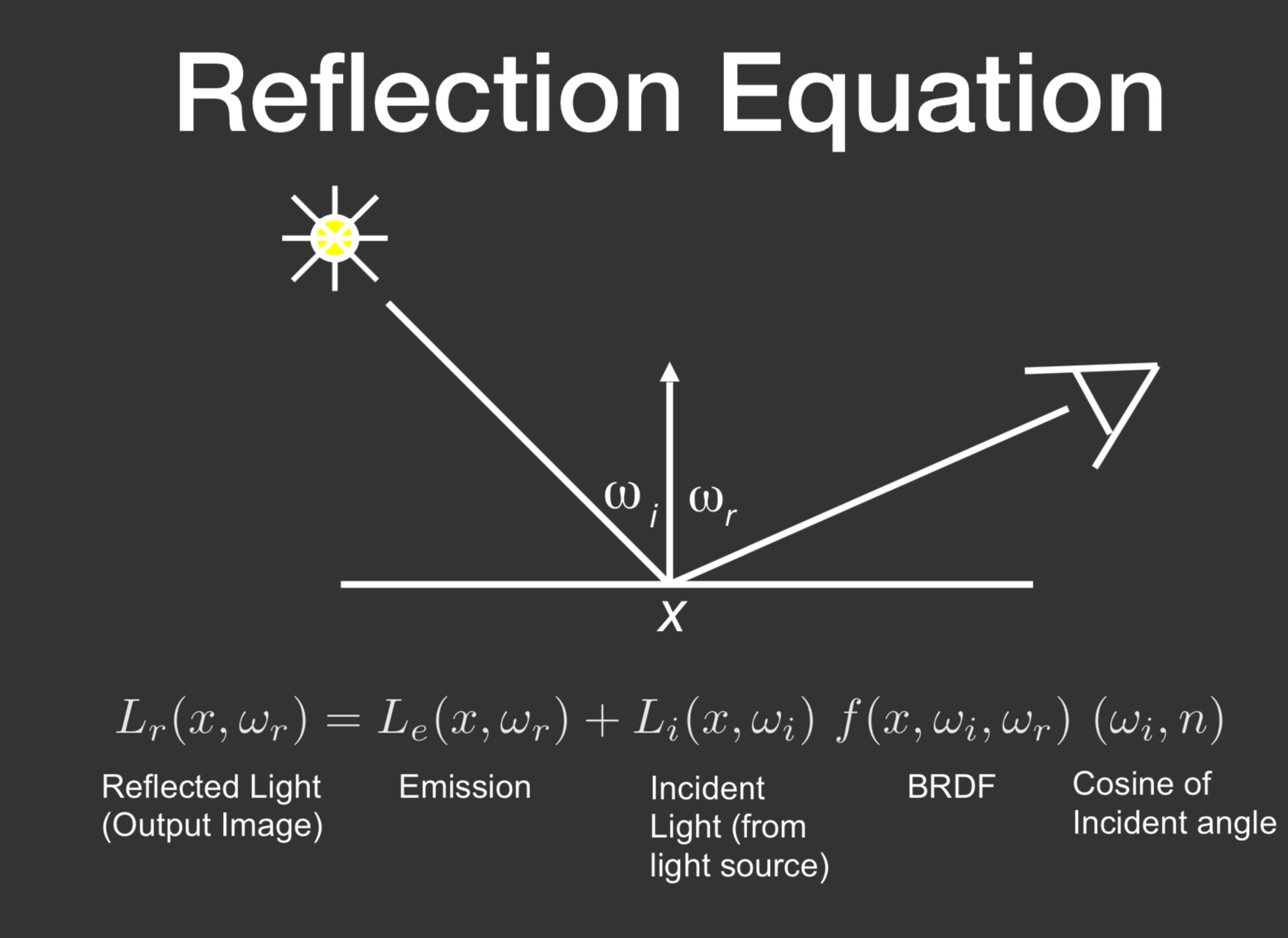
Lo(p, ω0) 是点p在出射ω0方向的最终渲染结果
Le(p, ω0) 是点p在ω0方向的自发光
fr(p, ωi, ω0) 点P和入射方向 ωi 到出射方向 ω0 的比例。也就是出射的分布函数。
Li(p, ωi) 是点p 和入射光方向ωi
n.ωi 是入射角带来的衰减系数。
通过一个方程描述所有的光线传播(仅限于物体表面)
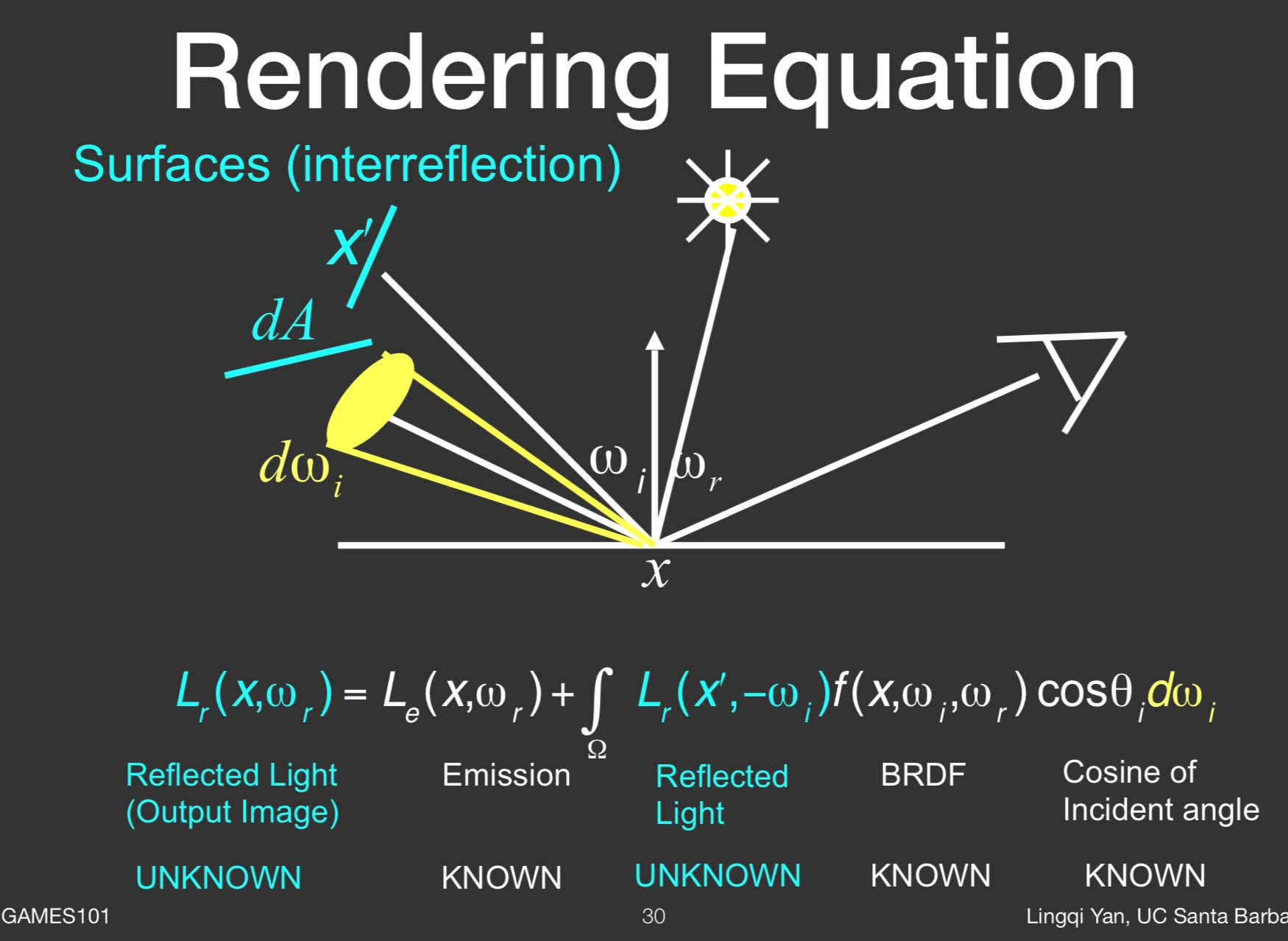
射出的radiance 可能成为其他点的入射radiance (此刻被照亮的物体本身作为光源存在了), 因此入射光不仅仅是单一的光源.
对于不发光物体,渲染方程就是反射方程。
发光物体,渲染方程 = 自发光 + 反射方程。
反射的光线取决于入射的光线 但是入射光线又取决于其他物体的反射光线, 因此存在递归问题。
公式说明
Le(p, ωo) 表示自发光
Ω+ OR H^2 表示半球
所看到的光 等于物体自己发出的光 + 从四面八方反射过来的光
PS : 这里的积分是因为面光源 面光源就是点光源的积分
PS: 注意和 BlinnPhong 一样, 虽然我们知道光是从外部射入, 但是规定上入射光的方向 ωi 是从内向外
PS: 渲染方程是定义在立体角上的
单一点光源的简单情况
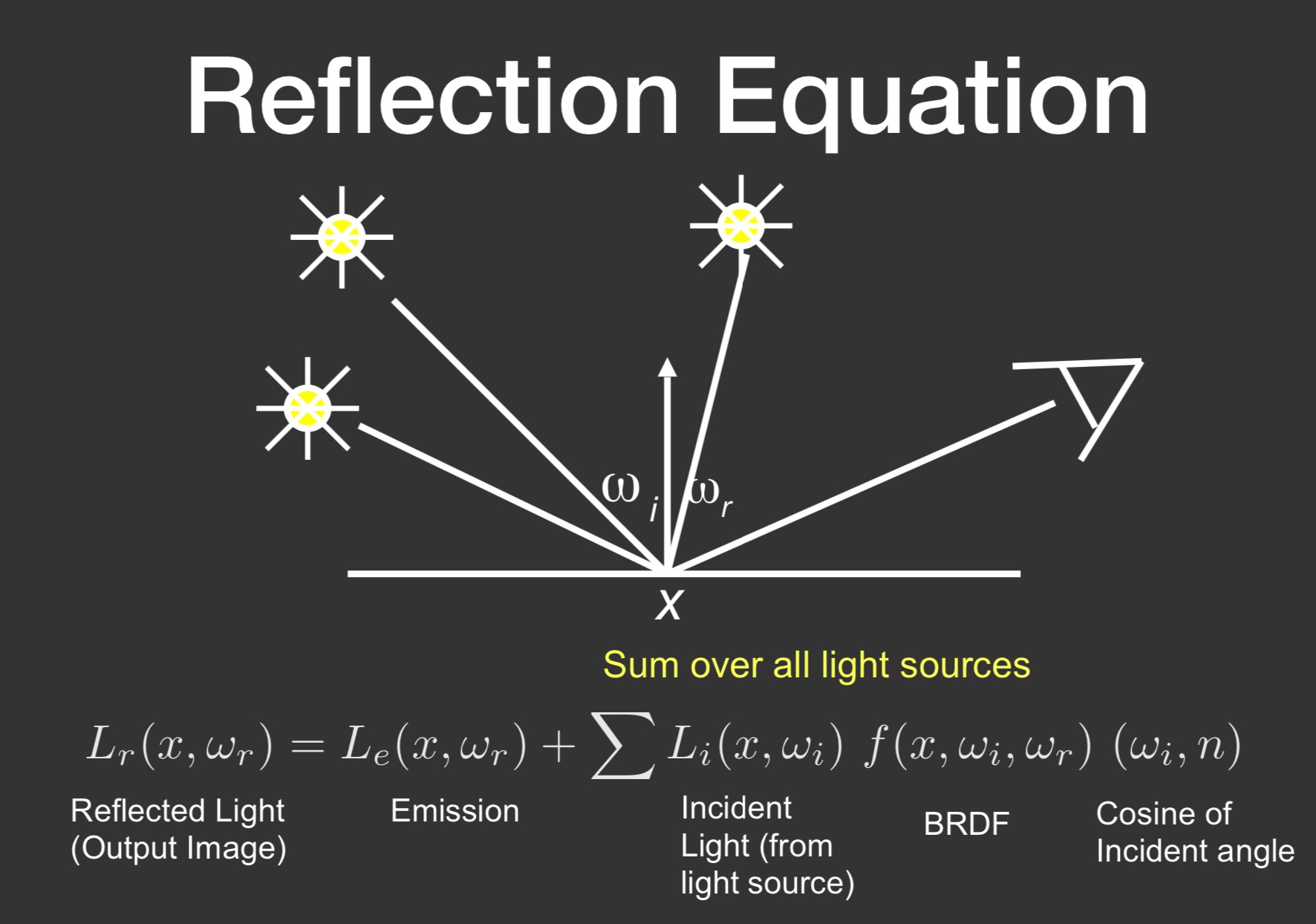
多个点光源的情况
当有一个面光源的时候
实际上就是把面光源当做多个点光源的集合, 对立体角做积分
但是对于其他物体反射过来的光应该怎么整?
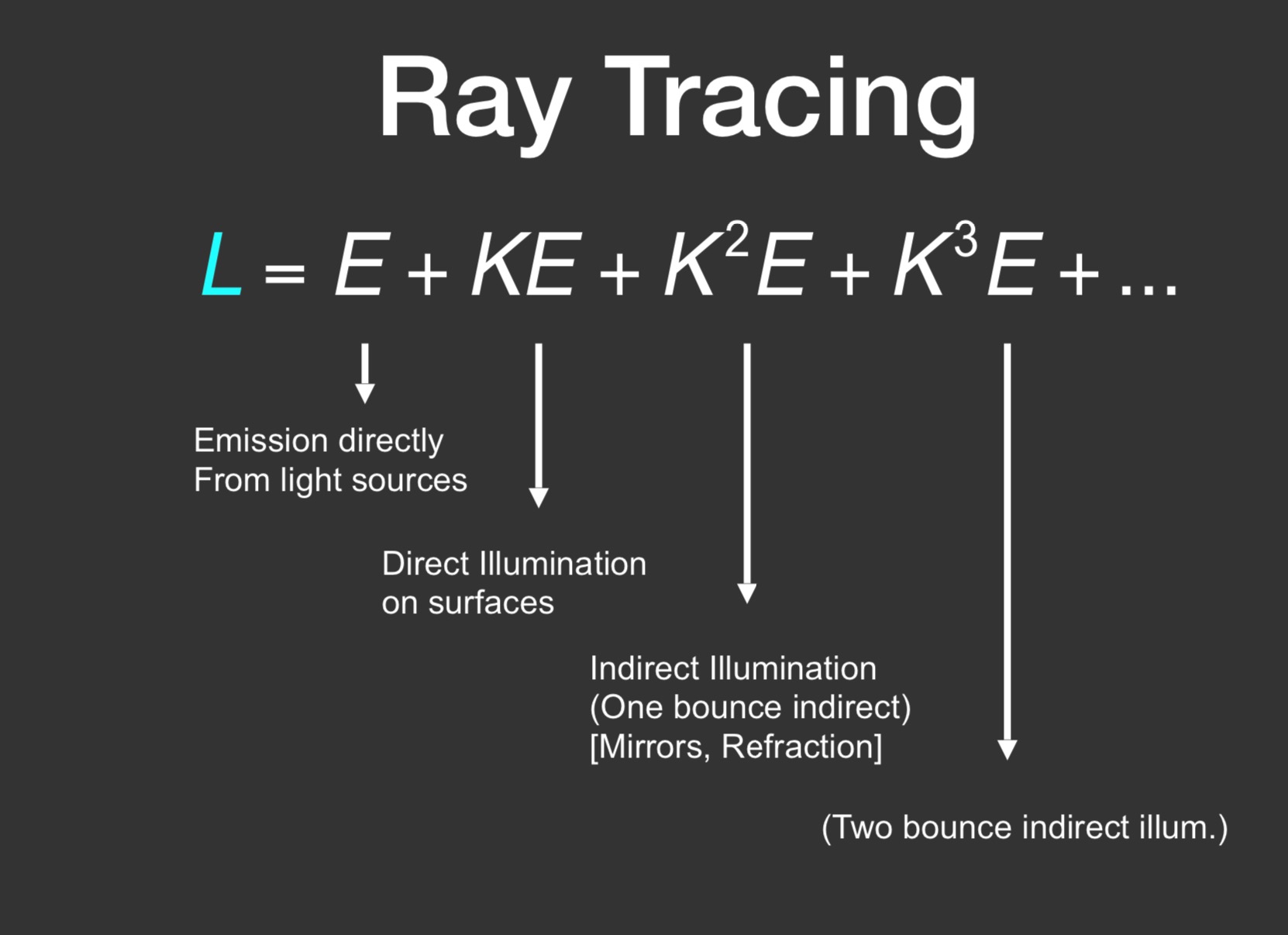
 PS: 把渲染方程简写为 L = E + KL 是为了后面解方程方便 (这里 L 是一个矩阵)
PS: 把渲染方程简写为 L = E + KL 是为了后面解方程方便 (这里 L 是一个矩阵)
全局光照是直接光照和间接光照的集合
PS: 光线追踪特别适合处理间接光照
根据之前的公式, 光栅化只能做自发光和直接光照 (当然实际上光栅化也可以做多次光照 只是比较难)
随机变量分布: 通俗的说随机变量根据不同的概率取不同的值. 取某些值概率大, 某些值概率小.
期望: 不断的取随机变量, 然后求平均.
描述连续情况下的概率和分布 (之前掷骰子的例子是离散情况)
PS: 仍然是微积分的思想, 把之前离散的取值(x=1, 2, 3 ..) 不断细分(x=1.11...1, x=1.11...2 ...), 使其成为连续的随机变量.
如同离散随机变量所有概率的和等于1 一样, 连续随机变量的积分最终结果就是1
双向反射是指地物的反射率随入射方向和反射方向而变化的特性 实际地物的反射都是具有方向性的,是入射方向和观测方向的函数。
https://www.cnblogs.com/mengdd/p/3237991.html
(Radiance versus irradiance)[http://sites.sinauer.com/animalcommunication2e/chapter04.02.html]