蒙特卡罗是为了解决定积分的问题
之前大学数学中学的求定积分的方法, 是先求出原函数再带入值. 对于一些复杂的函数是没有办法求到原函数的, 怎么办呢?
Riemann Integral，黎曼积分的核心思想就是试图通过无限逼近来确定这个积分值. 把积分区域分割为无数个细长的条.
目的: 求定积分
蒙特卡洛则是在积分区域内不断的采样, 采样很多次, 最后求平均值, 也就是面积.
PS: 这里的 N 是采样次数 N越大, 得到的结果越准
PS: 蒙特卡罗适合任何形式的积分. 37:13 ωi 是半球上的一个方向 p(ωi) 是 pdf 积分变成简单的求和平均
和之前的 Ray Tracing 有什么不同呢?
这种ray tracing 的特点是
- 当光线到光滑物体表面 沿着镜面方向反射 OR 折射方向折射
- 打到漫反射物体, 光线就停住
问题1 whitted形式的ray tracing 对于完全镜面的材质是OK的, 但是对于 glossy 材质的物体则有问题.
什么是 glossy
一般把完全镜面叫做 specular (mirror reflection)
没有镜面那么光滑(金属材质) glossy
问题2 同样, 对于漫反射, 其实也没有停下来, 光线还是会存在弹射, 反射到不同的方向上.
Whitted Style 有错误，但是渲染方程是正确的
求渲染方程的解
- 首先需要求出半球上的积分
- 另外解决递归问题
再次回忆一下渲染方程的定义
Lo(p, ω0) 是点p在出射ω0方向的最终渲染结果
Le(p, ω0) 是点p在ω0方向的自发光
fr(p, ωi, ω0) 点P和入射方向 ωi 到出射方向 ω0 的比例。也就是出射的分布函数。
Li(p, ωi) 是点p 和入射光方向ωi
n.ωi 是入射角带来的衰减系数。
关于此渲染方程 Read More https://zh.wikipedia.org/wiki/%E6%B8%B2%E6%9F%93%E6%96%B9%E7%A8%8B
注意⚠️ 此公式分母中的P略有歧义 分母中的P 表示PDF 函数，其他的p表示点p
如果是物体反射的光线怎么做？
假设入射光是来自点q 的反射光线
这里的红色部分shade(q, -ωi) 点p的入射方向 ωi 对于点q 来说，就是q 点的出射方向，因此加上负号
看起来很完美了！但是还没有结束。
不过目前仍有两个问题
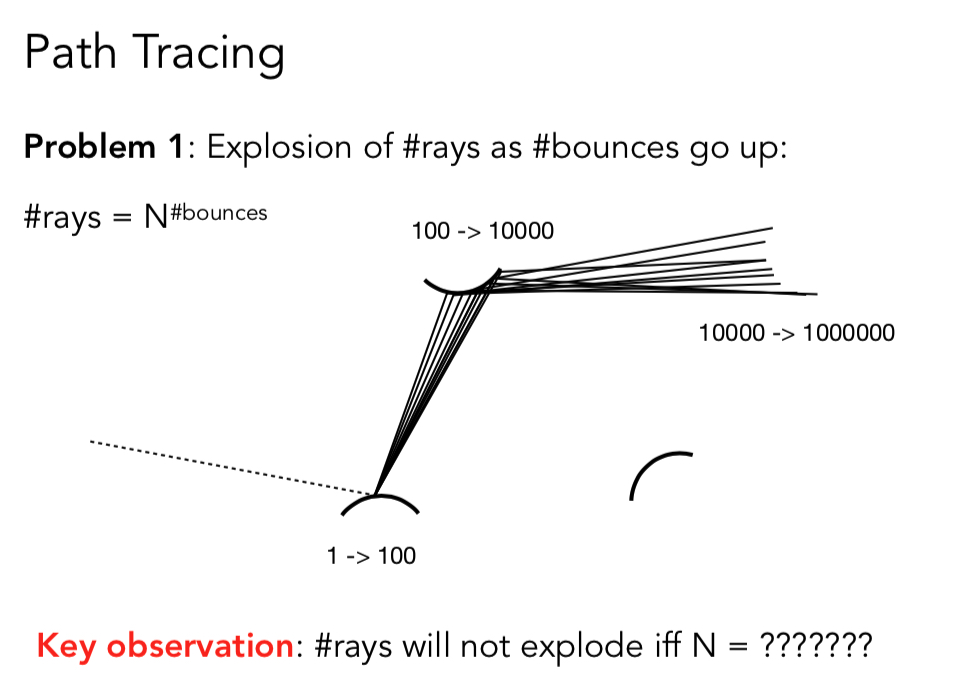
- 爆炸
- 递归没有停止
根据上面的做法 存在爆炸问题
N = 1时就是路径追踪， N !=1 分布式路径追踪， 存在指数爆炸问题
一个射线取100个样本射到一个物体上， 就有100个点，之后这100条线每一条都再发出100条光线，再次发出光线反射。
因为存在指数爆炸问题，只有 1 的 N 次方才不会存在爆炸问题。因此接下来每一条射线不再发散，每次打到一个点之后都再只发出一条射线。
但是这样会造成很多噪声，毕竟采样不够。
那么对每一个像素， 在每次光线打到物体反射都只再发出一条射线的基础上，多射出几条射线。
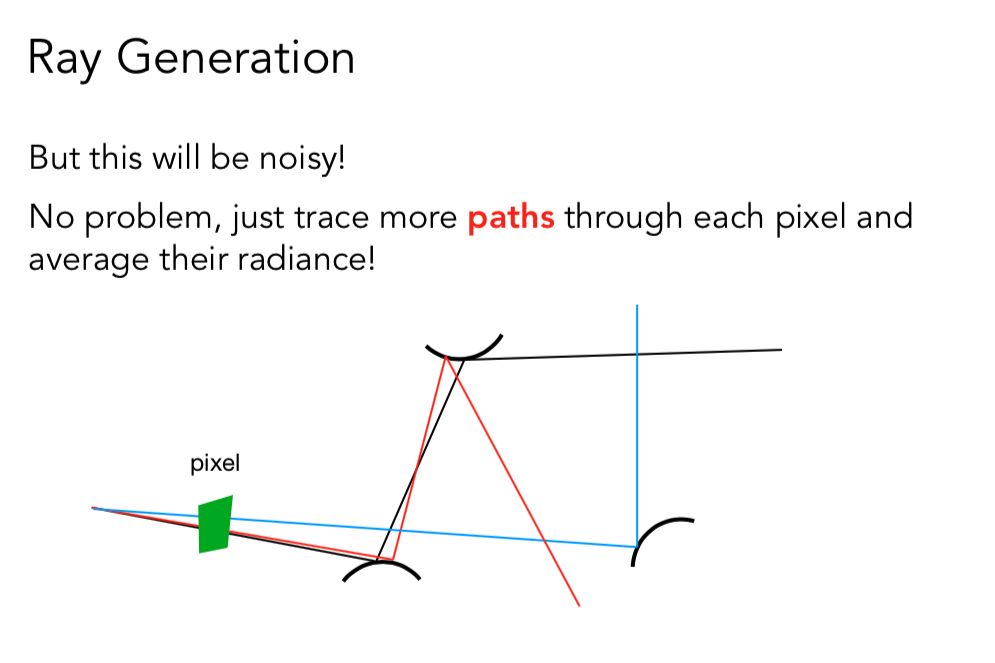
从参数可以看出 都是从一个相机位置出发， 向每一个像素所在方向发出射线。
上面提到递归没有停止条件， 现在通过俄罗斯轮盘赌方式，每次路径打到某一个点之后， 通过轮盘赌的方式决定路径追踪是否继续。
如果某次决定不再继续下去弹射，表示本次路径追踪到此结束。
这样科学吗？
根据公式算得的期望，得到的结果仍然是 Lo
现在已经是比较正确的Path Tracing 实现了， 但是不够高效。
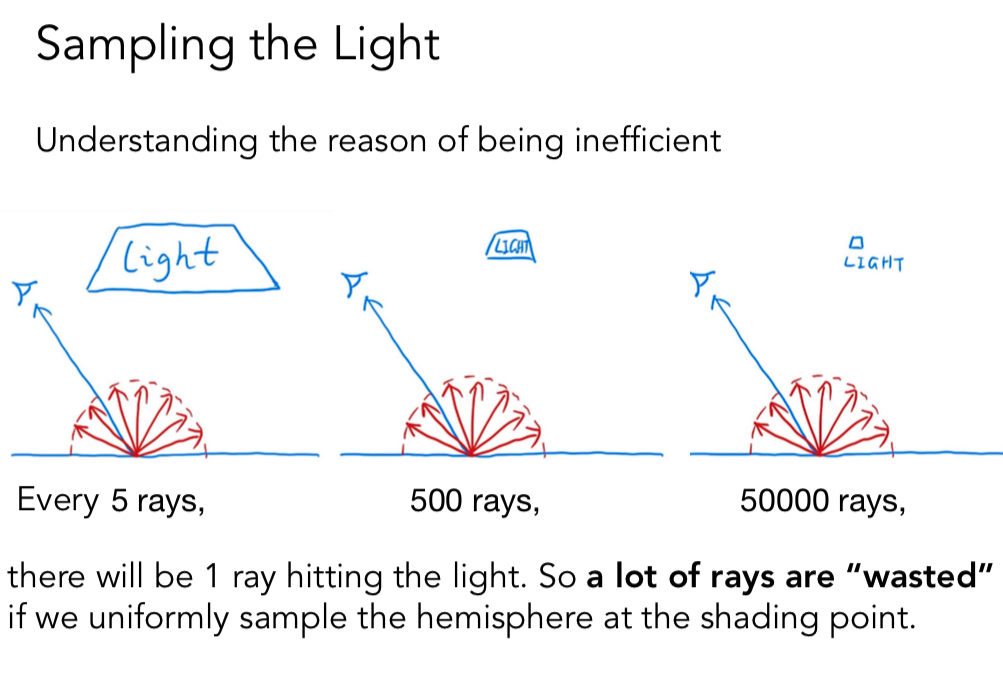
现在的实现存在计算浪费的问题
在着色点均匀的向外采样
当光源大的时候 在这个像素点可能取5个射线就能打到光源 当光源小的时候 在一个像素点可能取5万个射线才能打到光源
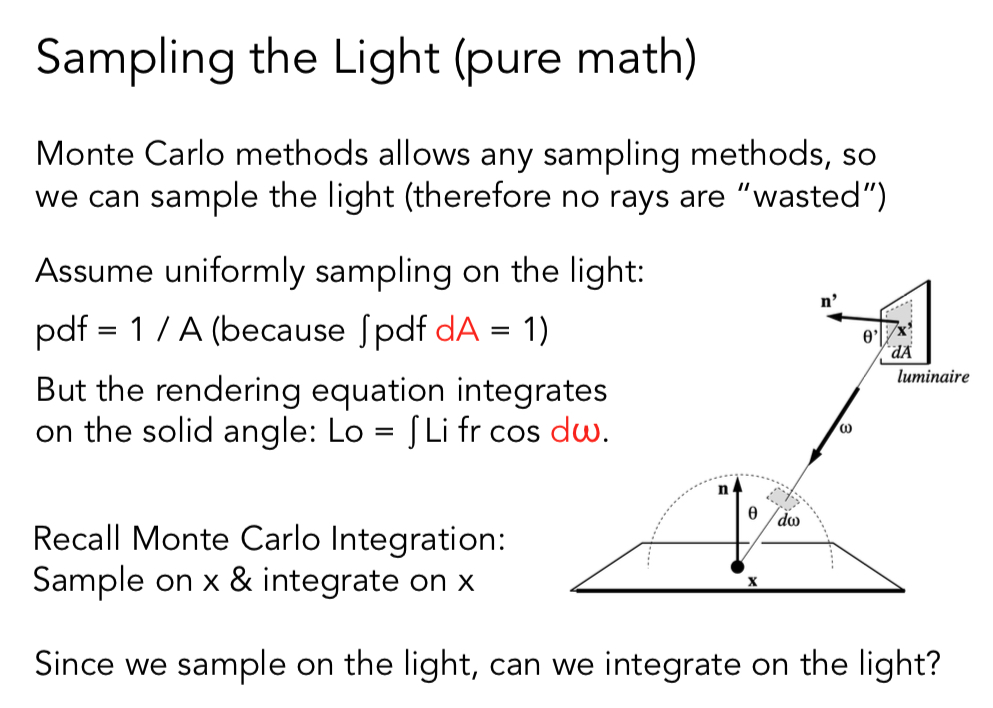
根据前面的定义， 蒙特卡洛积分要求是在X上面采样 最后就在X 上面积分 （这里的X是积分域）
我们能否在光源上采样， 并且不是像之前那样在立体角上积分，而是也在光源上积分呢？
PS: 有的地方也称为面积形式的的渲染方程， 并且将前面介绍的方程称为半球面形式。
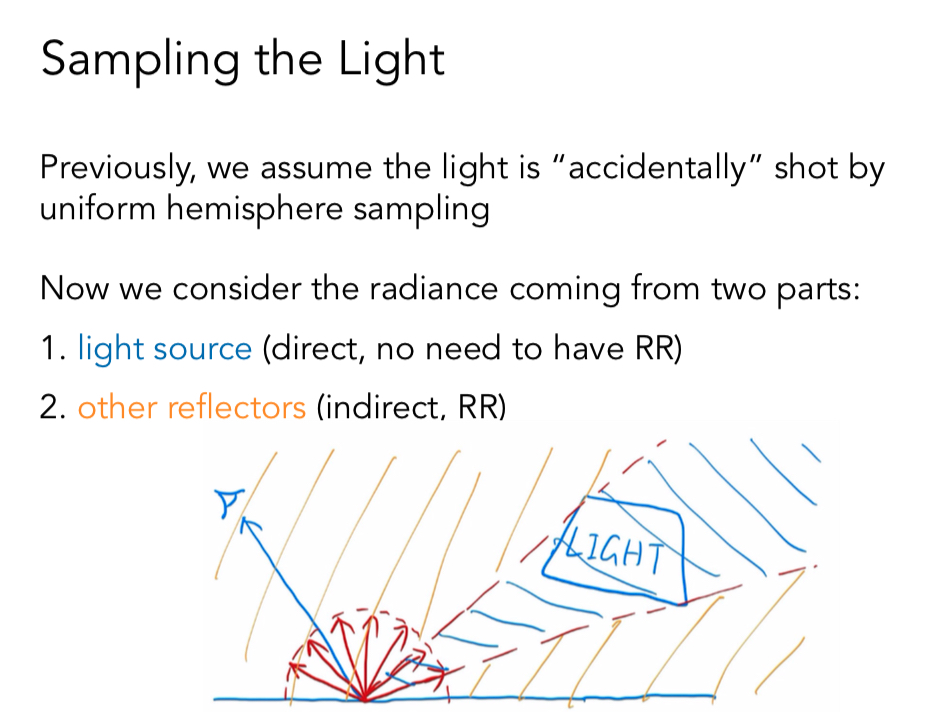
来自于光源的部分， 可以使用对光源采样。其他非光源的贡献，继续使用RR
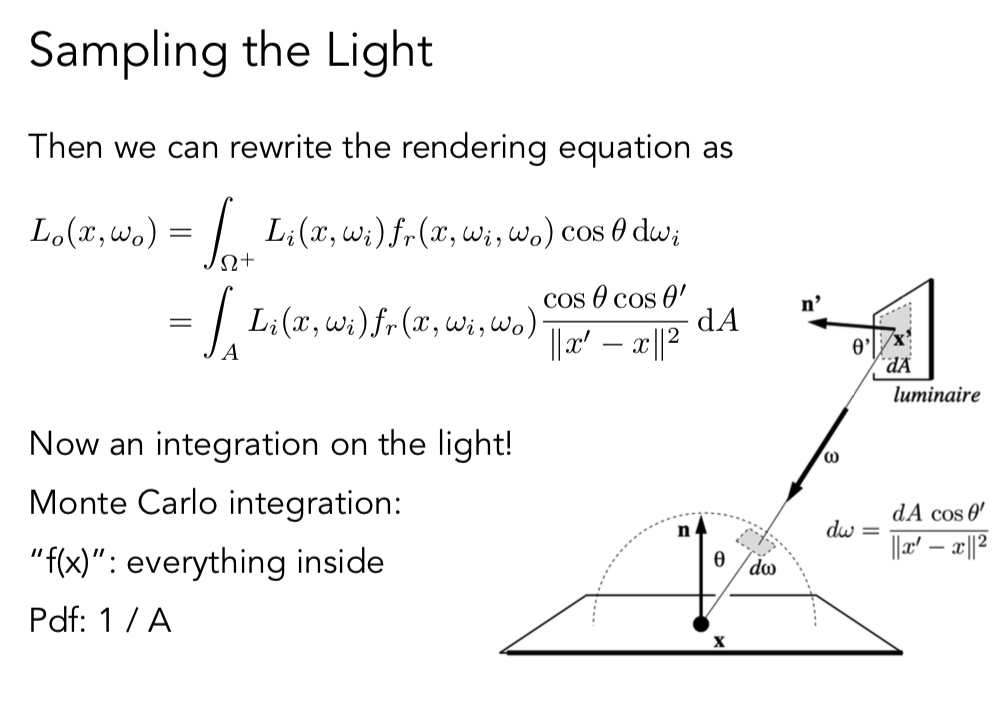PS dA 是光源上的一个小的表面
最终渲染方程的解
关于蒙特卡罗积分的详细介绍 Wyman的博客