Notes2.md

Lecture02

点乘

点积是数量积

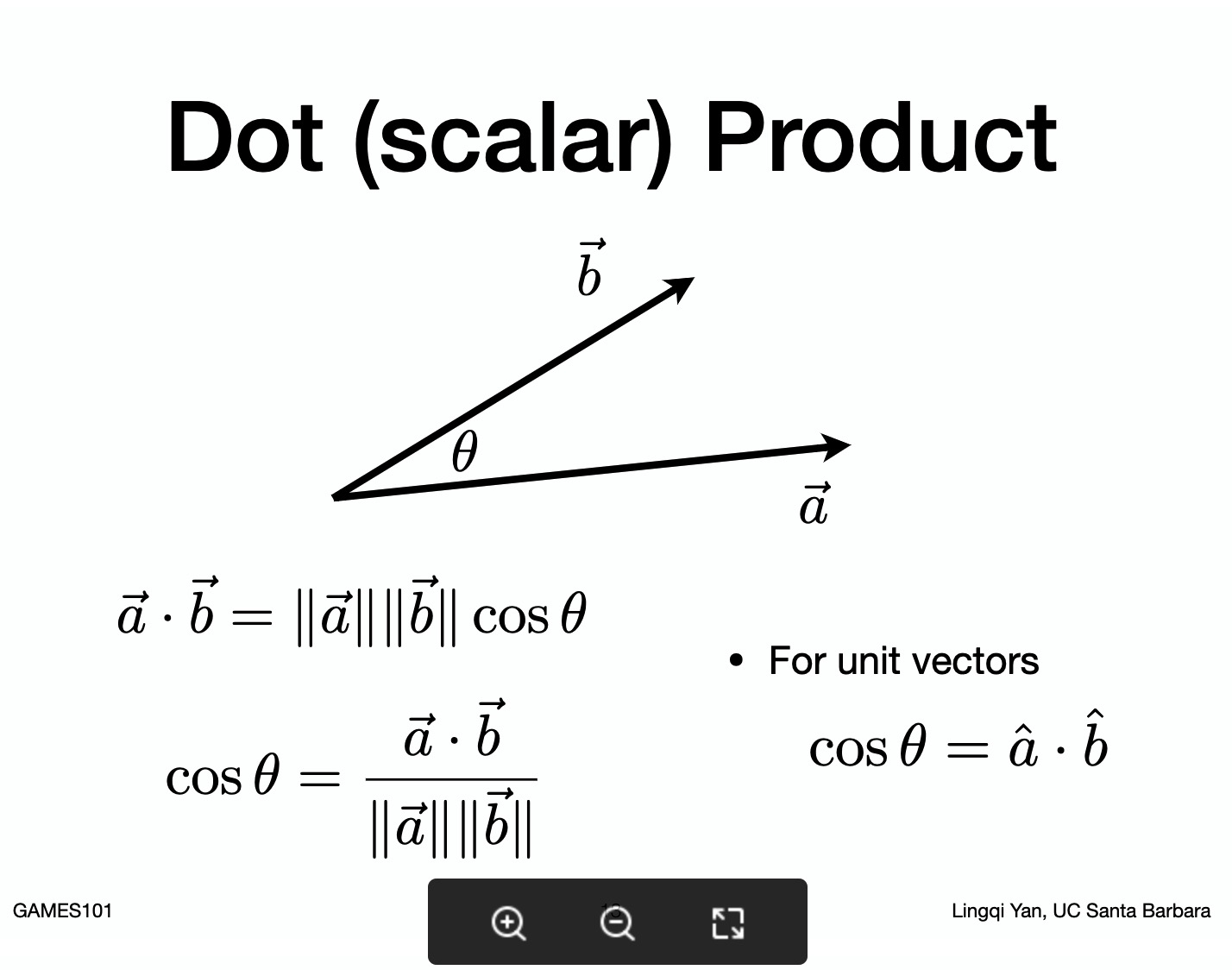
A·B = |A| |B| cos(θ).
|A| cos(θ)是A到B的投影

满足交换律和结合律

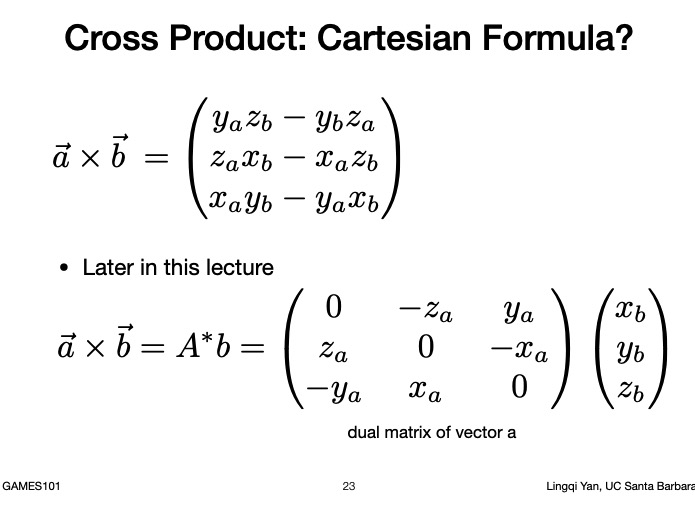
点乘的笛卡尔坐标系(直角坐标系)表示形式

点乘的几何运用

• Find angle between two vectors
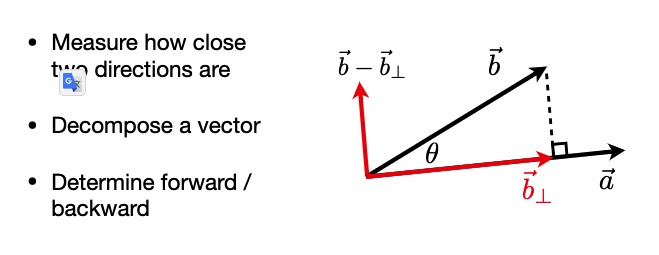
• Finding projection of one vector on another (向量分解)

向量 b 在a上的投影 b’ 其方向和a 相同 在得到b’ 后球另一个向量就容易了

点乘在图形中的运用

• 向量方向的接近程度
• 向量分解
• 方向是否相反(根据点乘的结果是否大于0)

叉乘

• 叉乘的结果是一个向量, 且和两个向量正交(垂直)
• 右手坐标系 右手螺旋定则 x 叉乘 y = z
• (如果是左手坐标系 x 叉乘 y 得到 -z 叉乘就是应用右手螺旋定则)

叉乘的笛卡尔方程表示形式

第二种是叉乘表示成矩阵形式

叉乘没有交换律 但是有结合律

叉乘在图形中的应用

• 判定左右 (同一个起点的两个向量 如何判定谁在谁的左侧 a 叉乘 b 得到的结果z 是正 那么 b 在 a 的左侧)
• 判定内外

矩阵

点乘 叉乘的矩阵表示形式

矩阵乘法没有交换律 但是有结合律分配律

• 结合律： (λμ)A=λ(μA) ； (λ+μ)A =λA+μA． A(BC) = (AB)C
• 分配律： λ (A+B)=λA+λB． A(B+C) = AB + AC

转置 (AB)' = B'A' (A + B)' = A' + B'

逆 (AB)" = B"A" (暂时用" 表示 -1) AA" = I