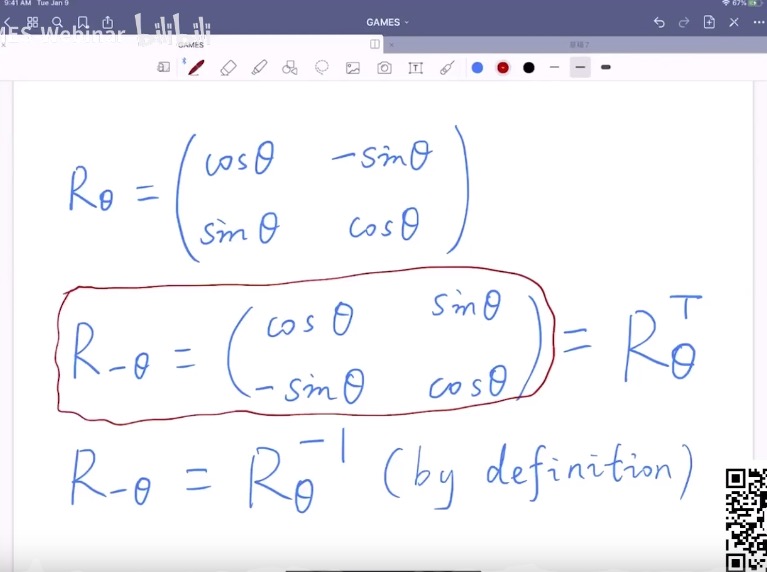
发现旋转 -θ 角度的矩阵, 就是旋转 θ 角度矩阵的转置
而是旋转 θ 角度矩阵的逆矩阵, 也是旋转 -θ 的矩阵
也就是说 旋转 θ 角度矩阵的逆矩阵 == 旋转 θ 角度矩阵的转置
根据定义, 一个矩阵的逆等于其转置, 那么这个矩阵是正交矩阵, 因此旋转矩阵是正交矩阵
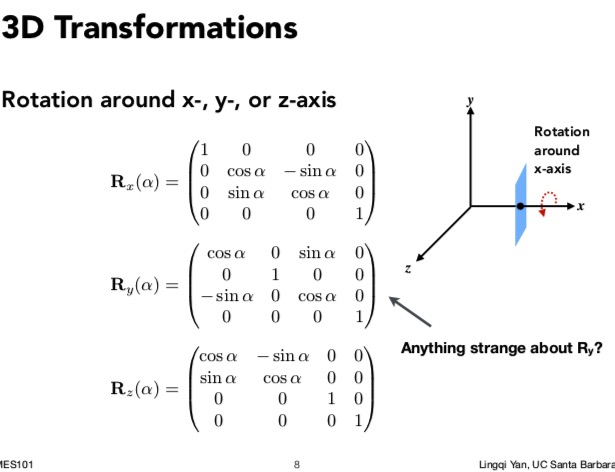
因为三维的旋转比较复杂, 因此先从某一个固定轴旋转开始. (逆时针)
Rx(α) 绕 x 轴旋转, y z 就相当于二维坐标中的 x y.
Rz(α) 绕 z 轴旋转, x y 就相当于二维坐标中的 x y.
Ry(α) 绕 y 轴旋转, z x 就相当于二维坐标中的 x y.
PS: 注意一下绕 Y 轴旋转. 矩阵中非0 1 的部分似乎和 绕x 绕y 有些不一样.
这是因为 x 是 y ✖️ z 得到 绕 x 旋转, 和 y ✖️ z方向一致. 我们在表示矩阵的时候, 也是 T ✖️ (x0, y0, z0)
z 是 x ✖️ y 得到 绕 z 旋转, 和 x ✖️ y 方向一致
而y 是 z ✖️ x 得到, 绕 y 旋转, 和 z ✖️ x 方向一致, 而我们表示矩阵的时候是 T ✖️ (x0, y0, z0)
所以这里的绕Y 的旋转, 相比其他两个轴, 存在一个转置. 所以Ry 1,3位置的元素不是 -sinα 而是 sinα
3D 中所有旋转都可以分解为绕轴旋转.
该公式描述了 空间内的任意一个向量V, 绕旋转轴k 旋转 θ 角度得到新向量 Vθ 的过程.
PS 绕旋转轴k 旋转 θ 角度 似乎看起来条件不够
实际上我们默认绕旋转轴k 就是这个物体在这个轴的原点作为起点做旋转
如果想绕着任意一个点旋转, 就是先将物体移动到轴的原点, 用上面的公式做了旋转之后再把物体移动回去
- 解决死锁问题
- 平滑插值
比如开始时物体旋转了15° , 最终目标物体要旋转25°, 中间如何平滑过度呢? 旋转矩阵矩阵并不适合做插值。此刻就需要四元数.
- view camera transformation
- projection transformation
- 正交投影
- 透视投影
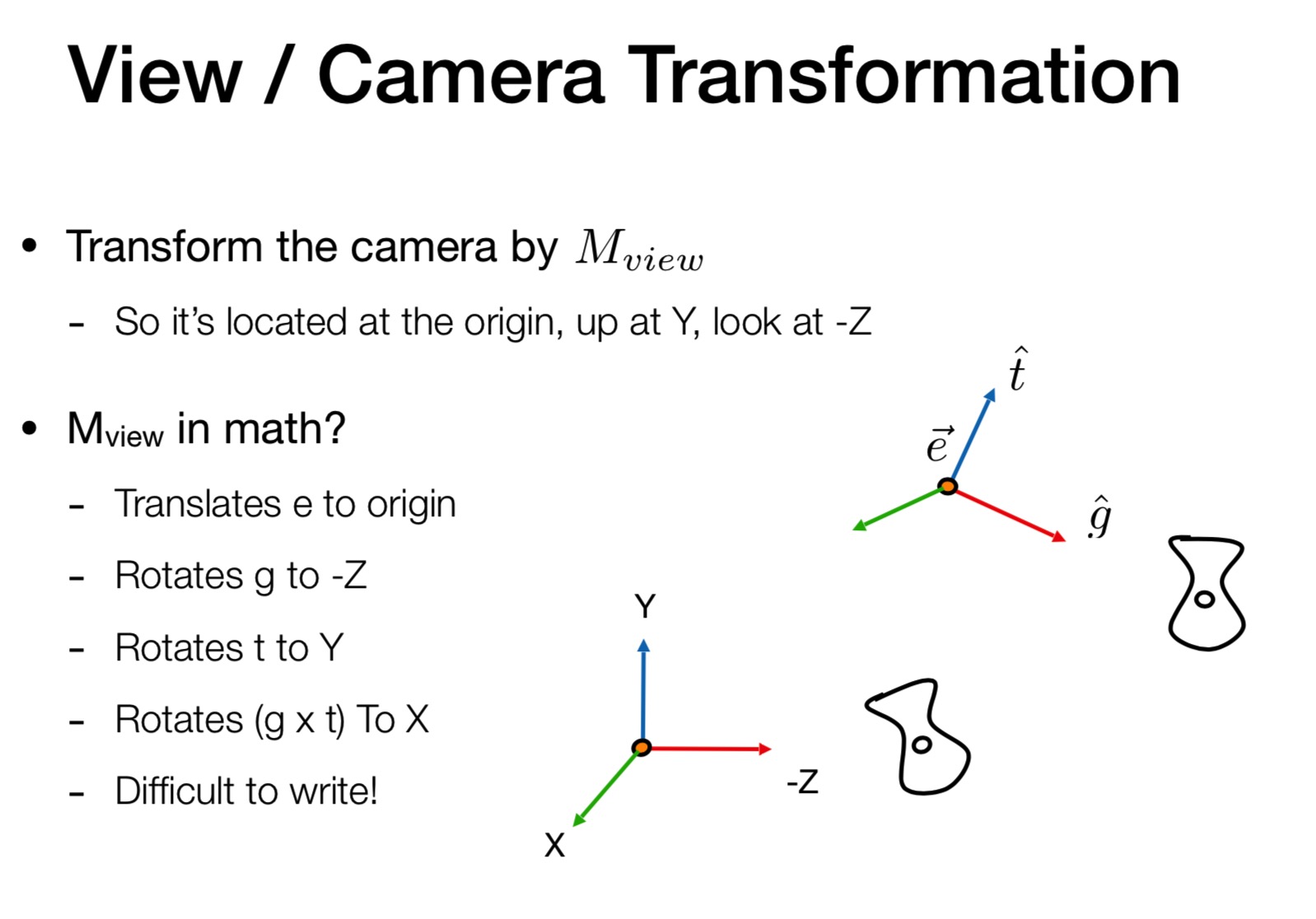
也被称为 modelview transformation
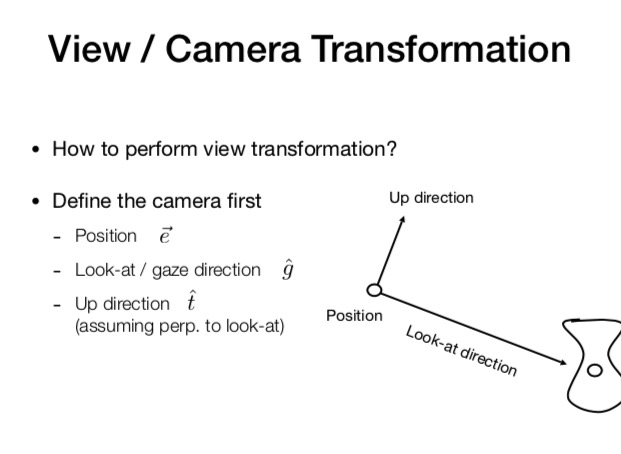
定义一个相机需要
- pos
- lookat
- up direction (前两个已经可以定义出相机镜头方向 up direction 就是镜头的旋转情况)
向量 e 表示相机的位置
向量 g 表示lookat 的方向 gaze
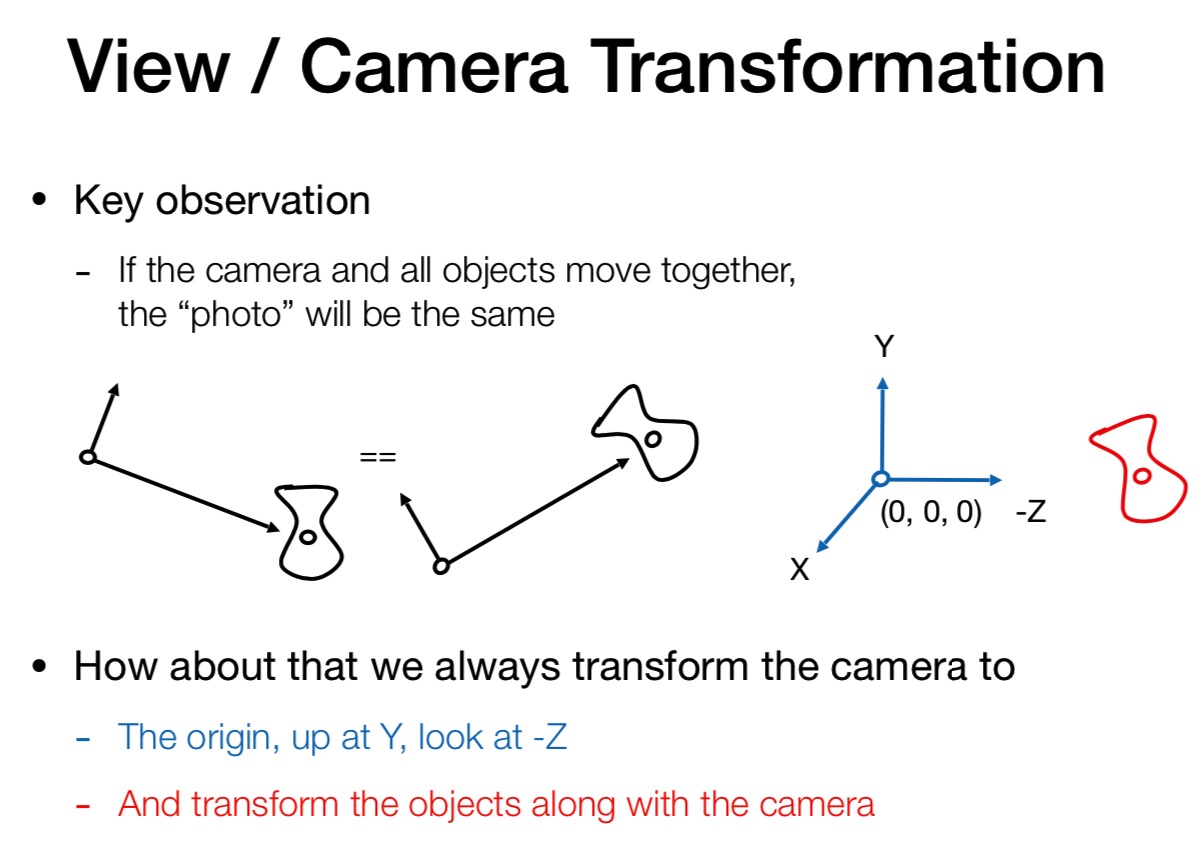
先让相机移动到原点 并且使得相机看向 -z 的方向, up 方向是 y 的正方向 (相机所拍的物体跟着相机都做上面的变换)
(让相机放在 0, 0, 0 位置是为了后续计算方便)
把相机放到上面规定的位置, 因此要做下面的旋转 Mview
rotate g to -Z 是因为根据约定, 相机永远看向 -Z 方向
rotate t to Y up方向旋转到 Y 方向
g to -Z 并不好写,因为 g 是一个很任意的向量, -Z 是一个轴,也就是一个单位向量。
但是反过来很好写 我们先写出 X Y Z 到相机位置的变换 那么相机到 X Y Z 就是刚才的逆变换
PS: Mview = Rview ✖️ Tview 先做平移变换 再做旋转变换
PS: 旋转矩阵是正交矩阵
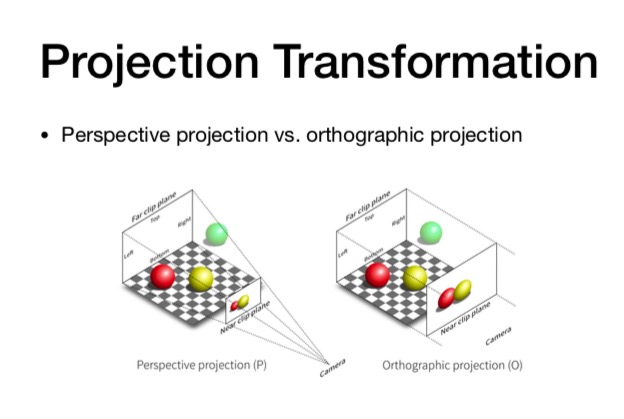
Projection is a Transformation. 投影是一种变换.
投影变换最终的效果是把各个坐标映射到 [−1 , 1] 之间,然后再乘以相应的屏幕高度和宽度,得到最终的屏幕坐标。 [−1, 1] 的坐标又成为NDC坐标
简单地理解方式: ( 关键操作: 扔掉 z 轴信息 )
实际上一般是这么操作:
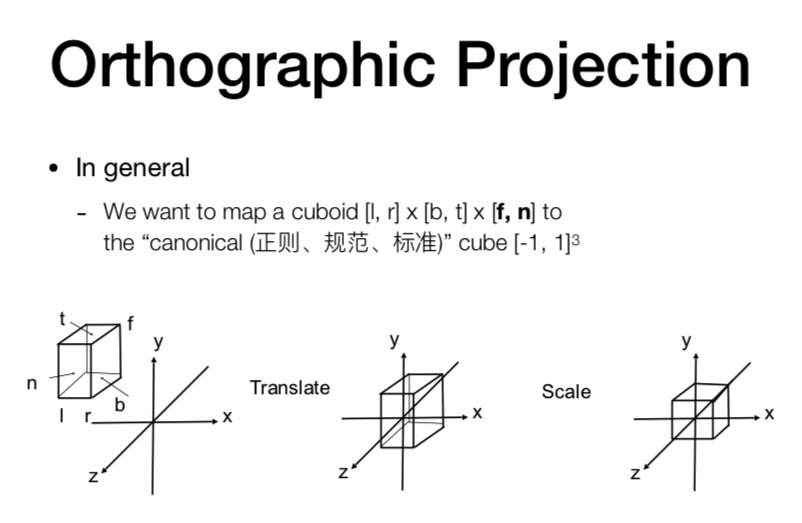
先确定视野范围(图中的矩形空间) 然后标准化( 规则观察体 )
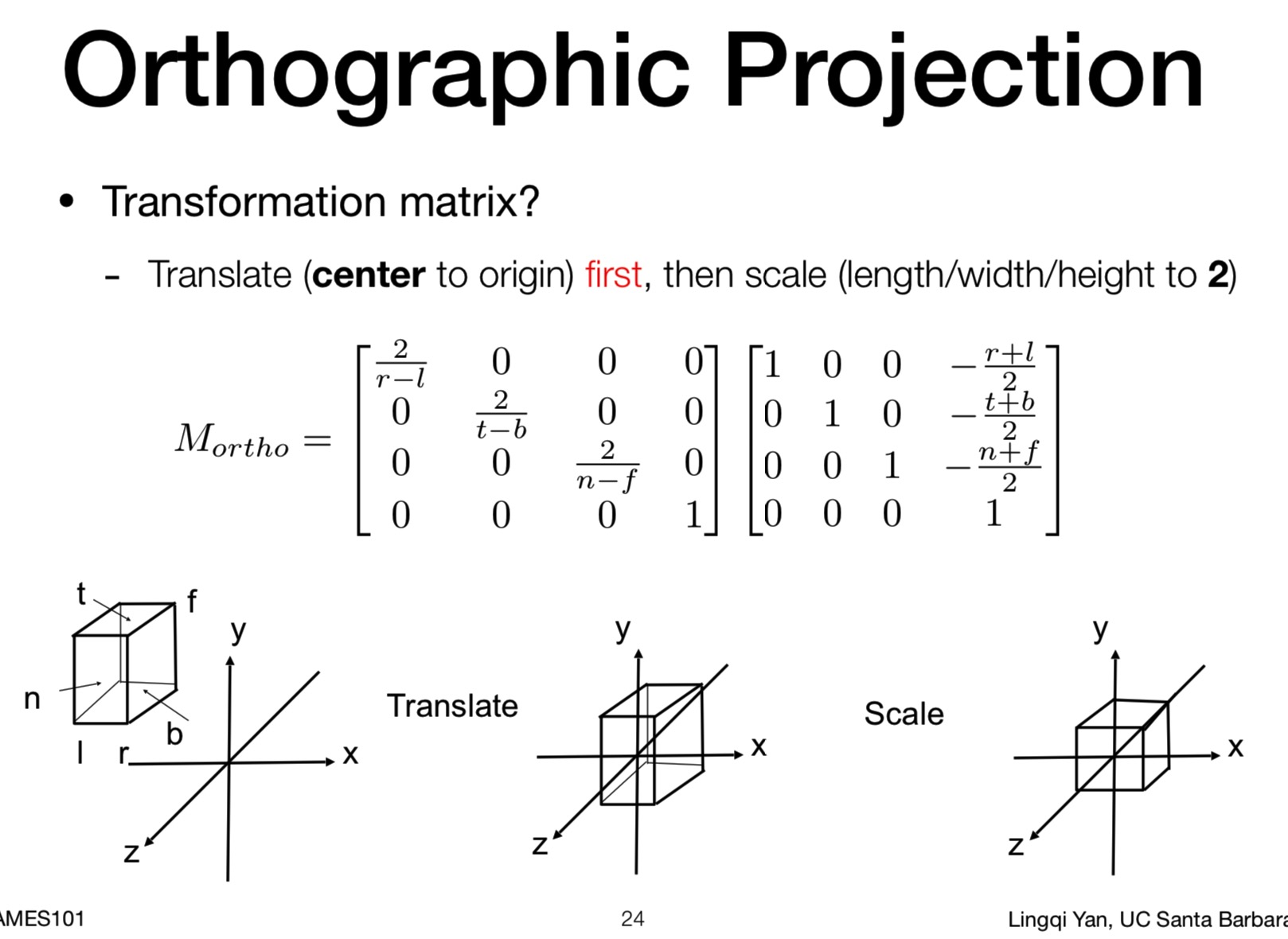
所以得到的矩阵变换如下
- 平移到原点
- 再缩放到标准立方体 (视锥体xyz 都缩放到 [-1, 1] 的范围)
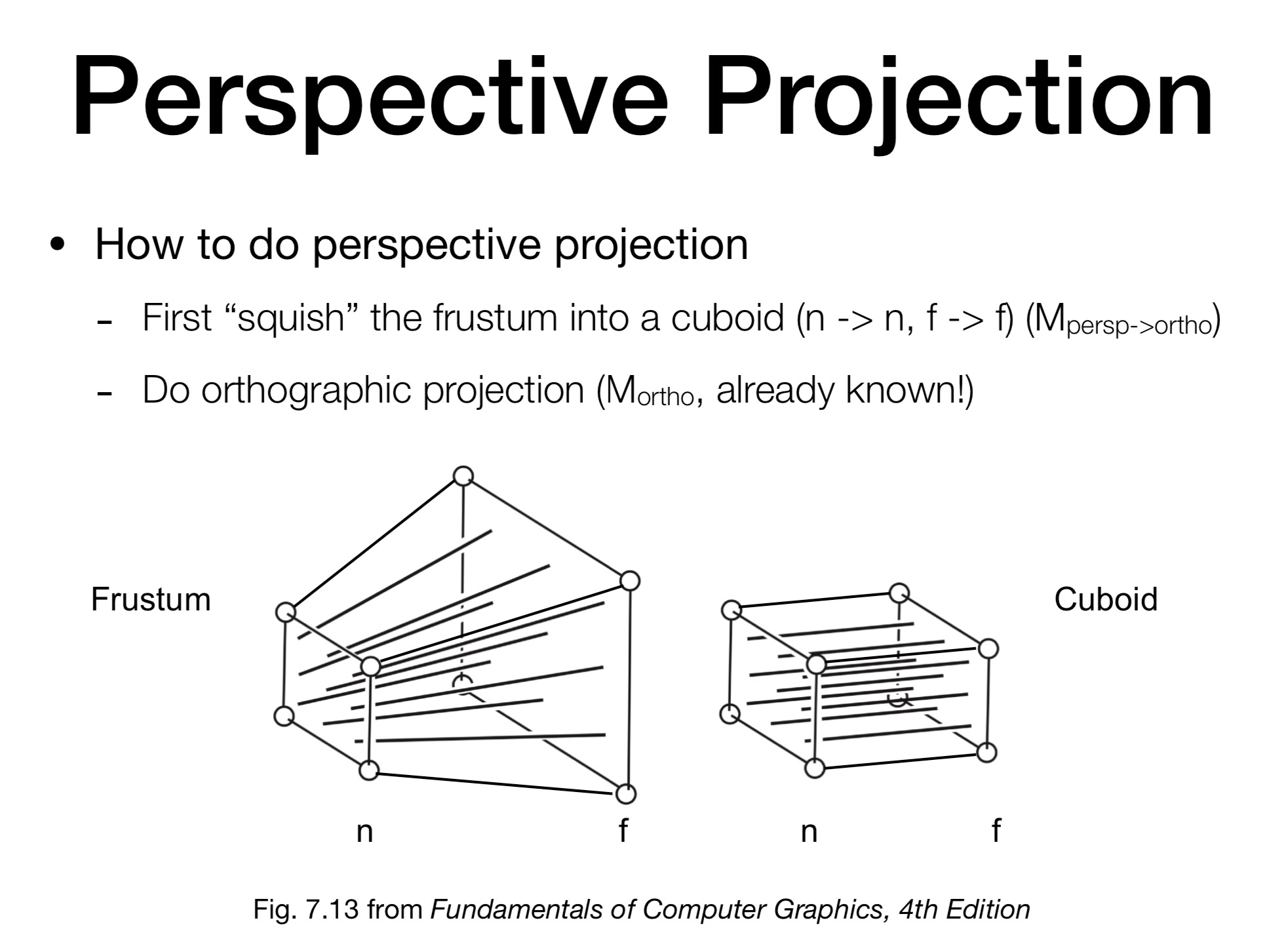
先挤压视体, 使其成为一个长方体, 那么问题就变为了正交投影.
这个挤压要保持下面的性质
- 近平面的任何点在挤压前后不会变
- 远平面的 z 值不会发生改变
- 远平面的中心点位置不会改变
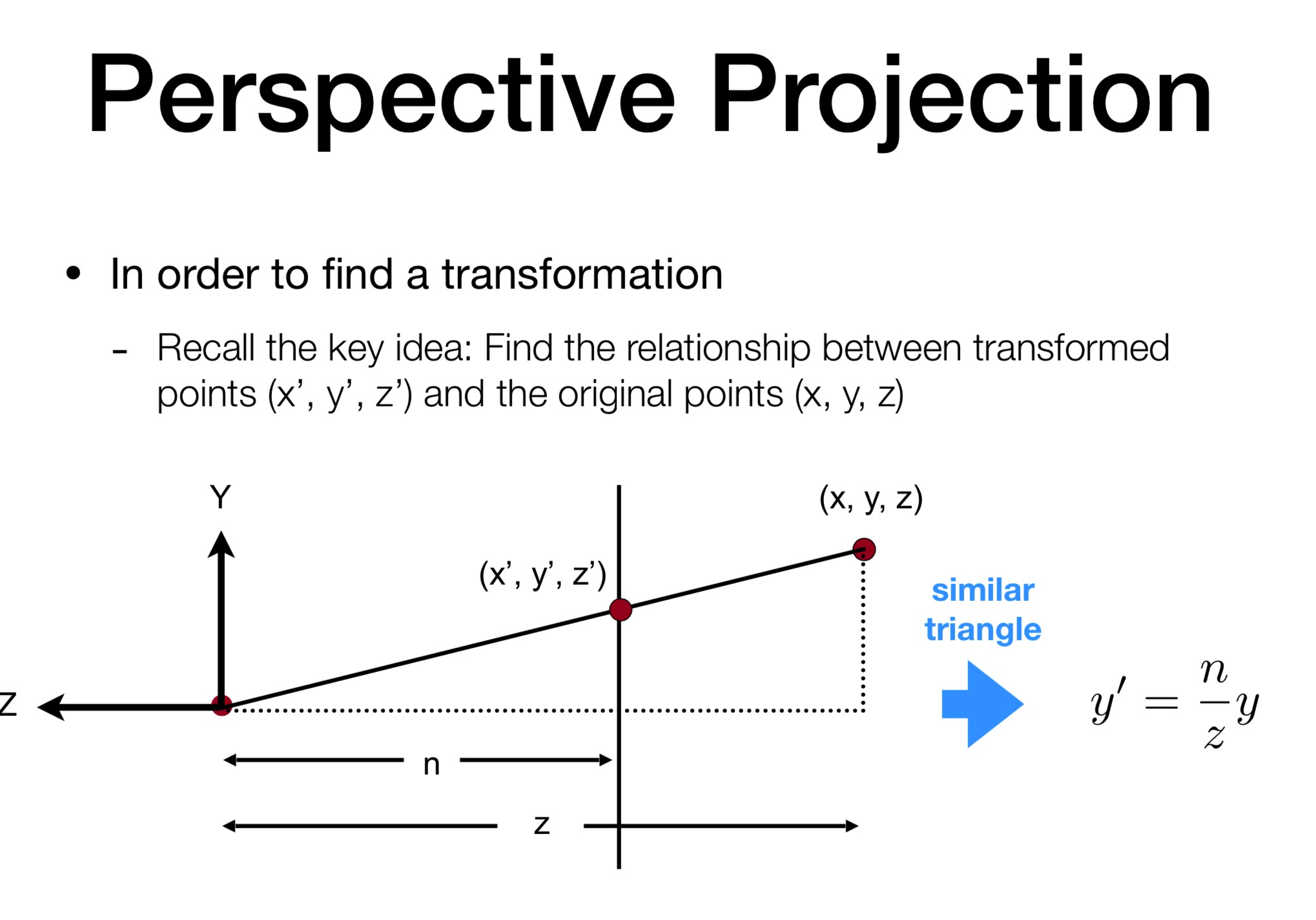
最左侧的那个实心小点 代表相机的位置 Y 画出了相机的Up 方向. 从 Z 方向说明相机正向 -Z 方向看.
原本的 y 在挤压之后变为 y' 根据相似三角形就可以得到上面的结果
PS: 我们只知道近平面和远平面 z 值不变, 中间z 是否变不确定.
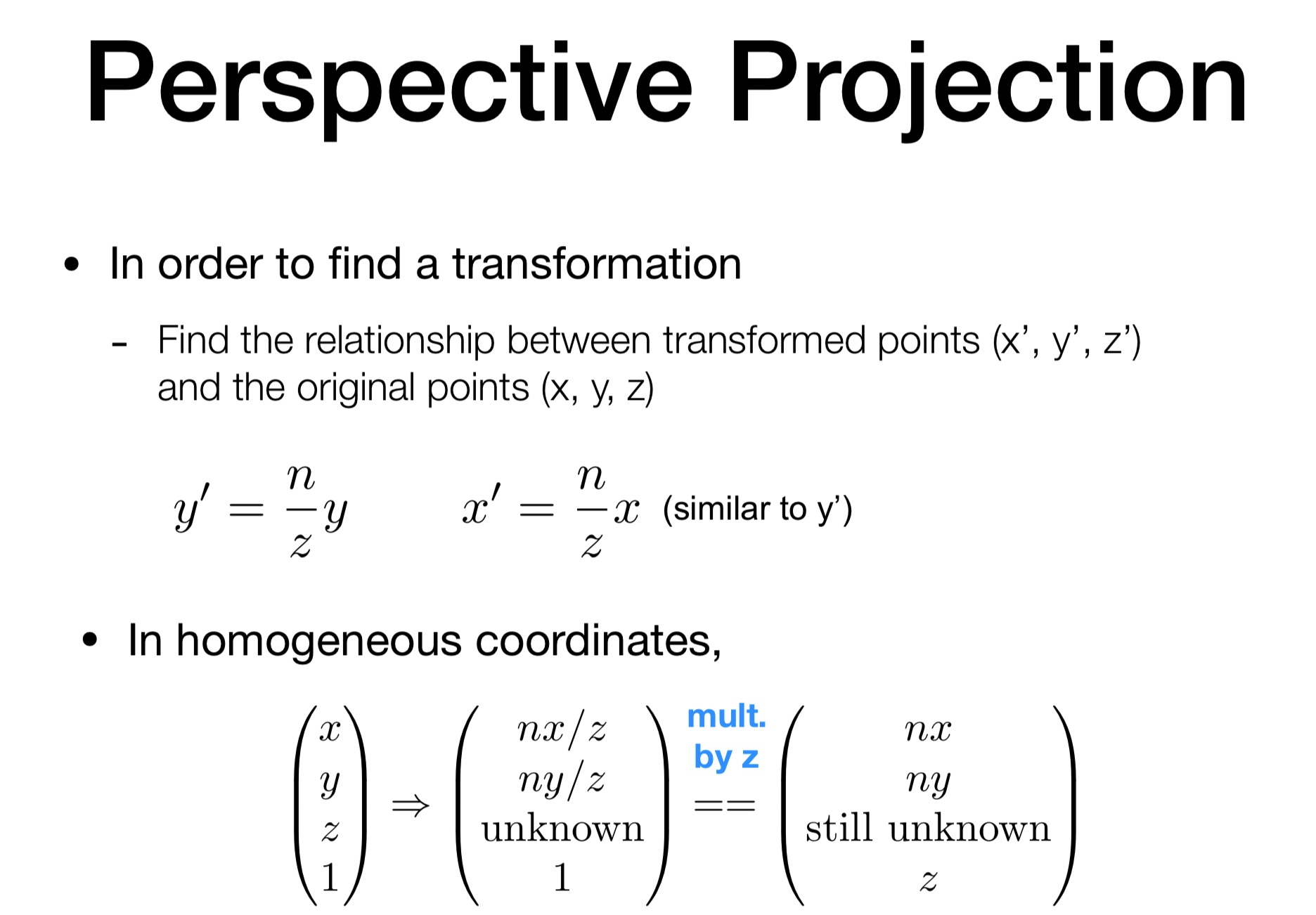
根据相似三角形, 已经可以推出部分矩阵了
现在只剩第三行不知道了
根据近平面的点变换之后不会变, 也就是(x, y, n, 1) => (x, y, n, 1). 另外根据其次坐标变换一种表达形式 (nx, ny, n^2, n)
就可以得到第三行应该是 (0, 0, A, B) 的形式.
(因为得到的结果是 n^2 也就是 xy 的部分都是0 )
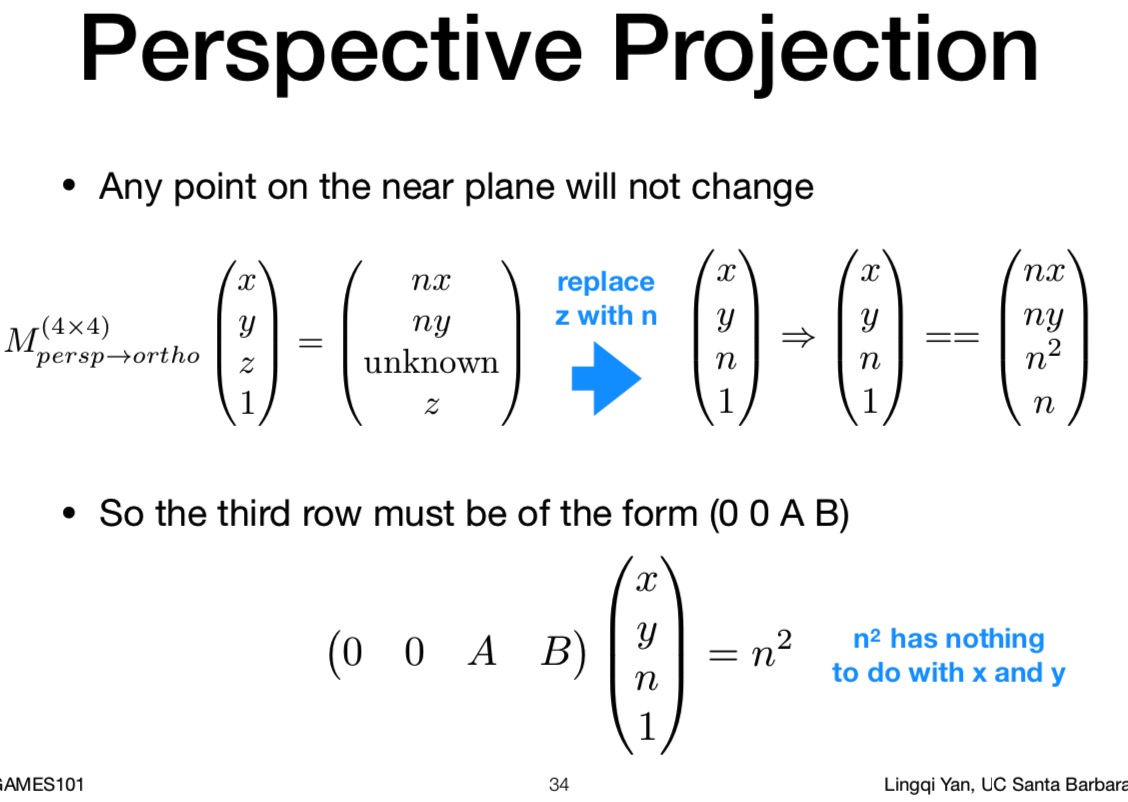
PS: 注意这里最后 (0,0, A, B)那一块是简写 只写了透视矩阵的第三行 最后的 n^2 是说透视 矩阵✖️ (x, y, z, 1) 得到的第三行的值
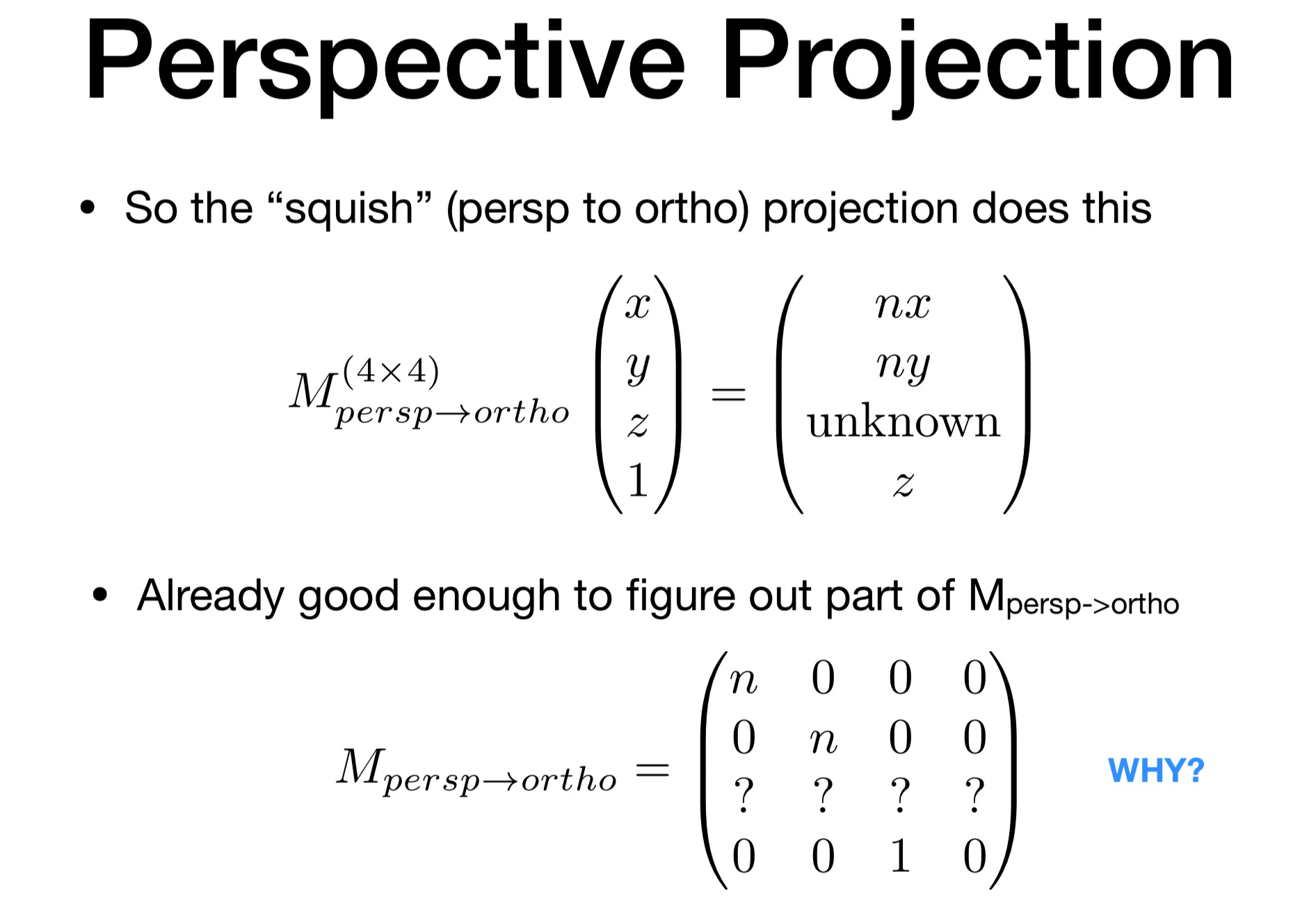
另外再根据变换后远平面的 z 值不改变, 就可以得到一个方程组.

那么透视投影矩阵就是
n 0 0 0
0 n 0 0
0 0 n+f -nf
0 0 1 0
经过这个变换之后 两个面中间的 z 会怎么改变? 是更偏向 n 还是更偏向 f
- 正交矩阵每一列都是单位向量,并且两两正交 (单位向量就是长度为1 的向量)
- 正交矩阵的逆(inverse)等于正交矩阵的转置(transpose) 且行列式的结果只能1 OR -1
https://www.zhihu.com/question/316200199
正交矩阵之所以叫正交矩阵,是因为一套正交基向量在该矩阵变换下仍然是正交的,这是正交矩阵的充分必要条件。很明显的,任何两个向量在旋转矩阵的变换下,这两个向量仍然是正交的,所以旋转矩阵是正交矩阵
B站有个回答说的很好
https://www.bilibili.com/video/BV1X7411F744?p=4
AT 12:46, 这是因为二位平面定义时,逆时针实际是在三维从z正向看,因此3维绕y旋转,逆时针实际是z向x转,但是旋转矩阵的行列对应关系是x向z转,取逆(转置)就得到了
首先把 把左右手坐标系 x 方向都朝一个方向.
左手坐标系远的物体 Z 值越大, 但是右手坐标系是远的物体 z 越小.
这一点左手坐标系上更加直观.
https://zh.wikipedia.org/wiki/%E8%A7%86%E4%BD%93 视体(英语:viewing frustum)又称视景体、视锥,是三维世界中在屏幕上可见的区域,即虚拟摄像机的视野。