Part II 反走样Antialiasing (俗称抗锯齿)
Artifact 在图形学中的含义: 一切和预想的不一致的表现的情况
摩尔纹moire: 采样带来的问题, 在一个像素上有过多的频率的变化
走样出现的根本原因: 信号的变化速度太快, 而采样频率跟不上信号的变化速度
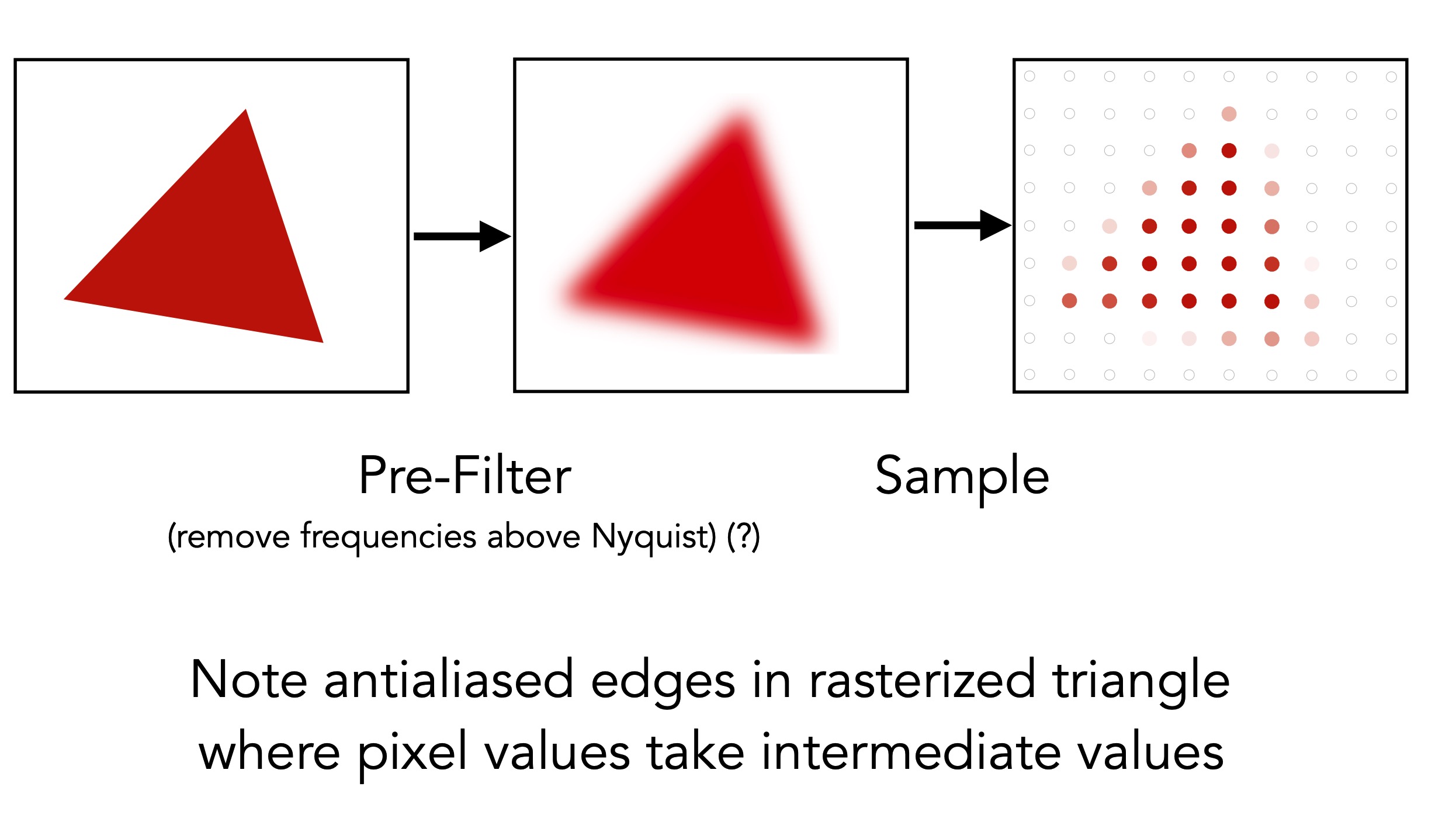
解决办法之一: 先模糊 再采样
但是, 为什么这样可以解决问题呢?
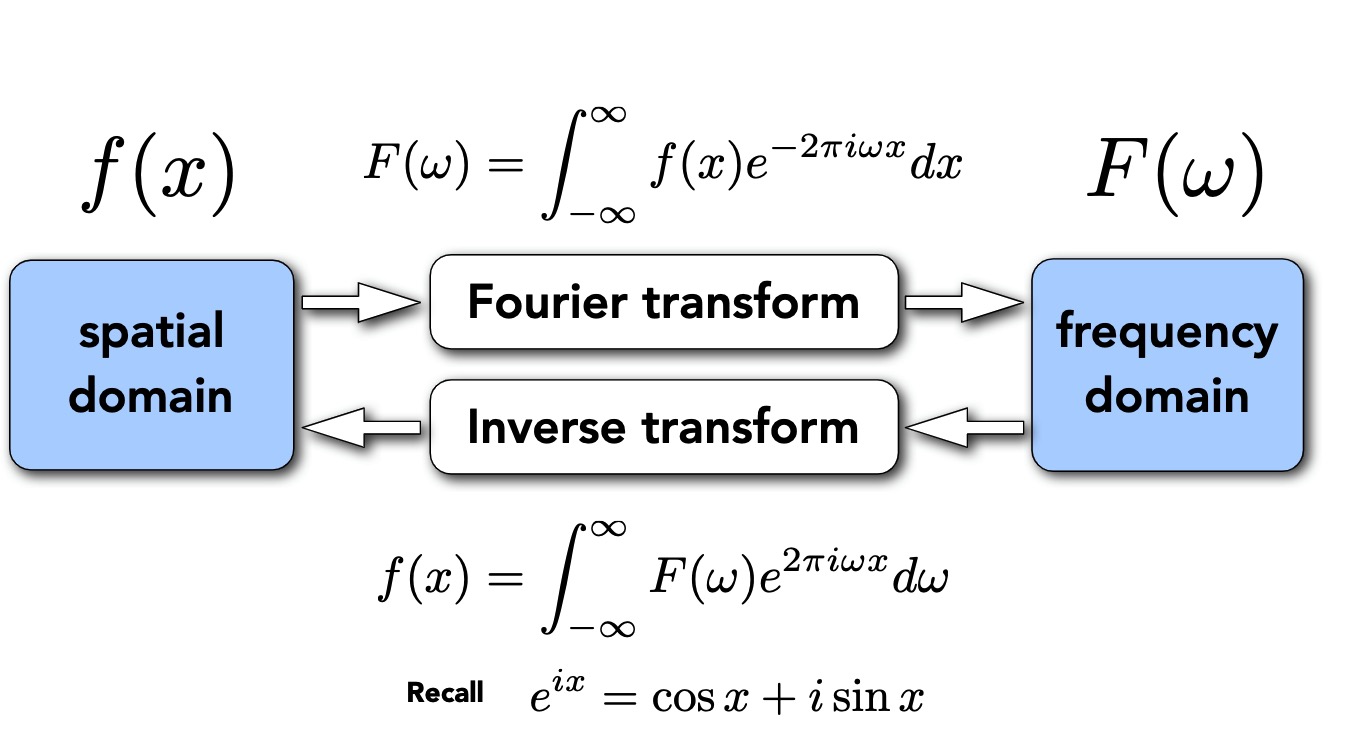
傅立叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合 百度百科 更注重数学上的概念
傅里叶变换 是一种线性积分变换,用于信号在时域(或空域)和频域之间的变换, wiki 更注重于时间域频域
蓝色是实际信号 圆圈是采样点 黑色是根据采样得到的点拟合的信号 可见由于采样频率不够 导致错误
低通滤波和高通滤波
滤波(Wave filtering)是将信号中特定波段频率滤除的操作
low pass filter & high pass filter
高通滤波 — 只允许高频信号可以通过, 去掉低频信息 — 保留图片上的轮廓 — 轮廓素描
低通滤波 — 只允许低频通过 , 去掉高频信息 — 去除图片上物体轮廓 — 模糊
滤波 == 卷积操作 == 求平均
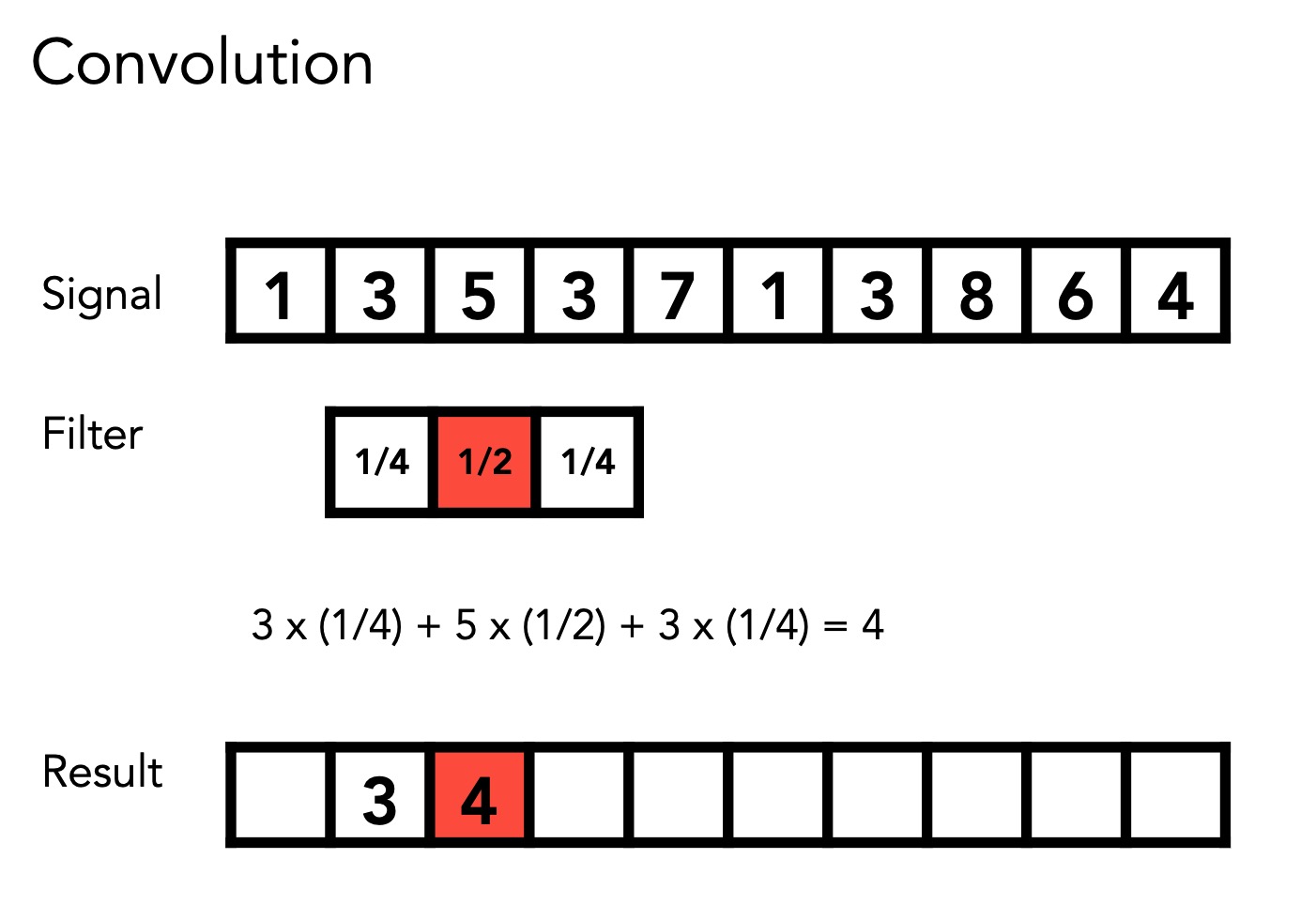
Convolution (下面是图形学中的简化版本 并不是数学中的定义)
卷积在移动窗口的过程中 把窗口覆盖的信号和对应的过滤器做点乘然后求和 结果写回窗口的中心值
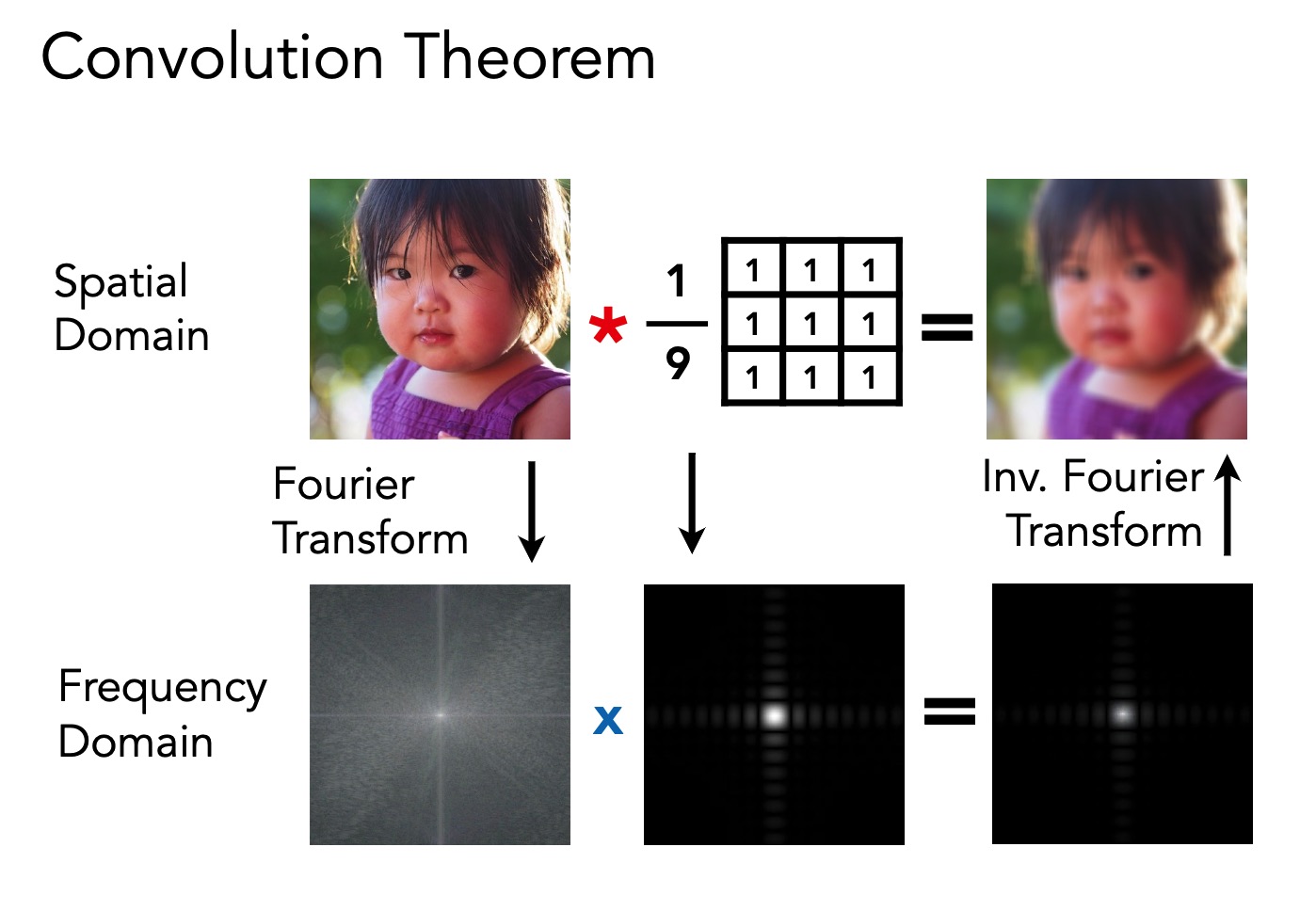
时域卷积 等于 频域乘积
时域的乘积 等于 频域上的卷积
Sampling = Repeating Frequency Contents
这里 a 是原本的信号, 然后用 c 对其 采样, 最后得到 e (a 是连续的, 经过采样之后得到了一堆离散的点),
这里 a c 都是时域 ( c 是冲激函数 ) b d 分别是他们的频域
a c 的乘积 e 就是 b d 的卷积 f
通过 f 图可以看起来就是对 b 图的复制粘贴
因此定义 ==> 采样:重复原始信号的频谱
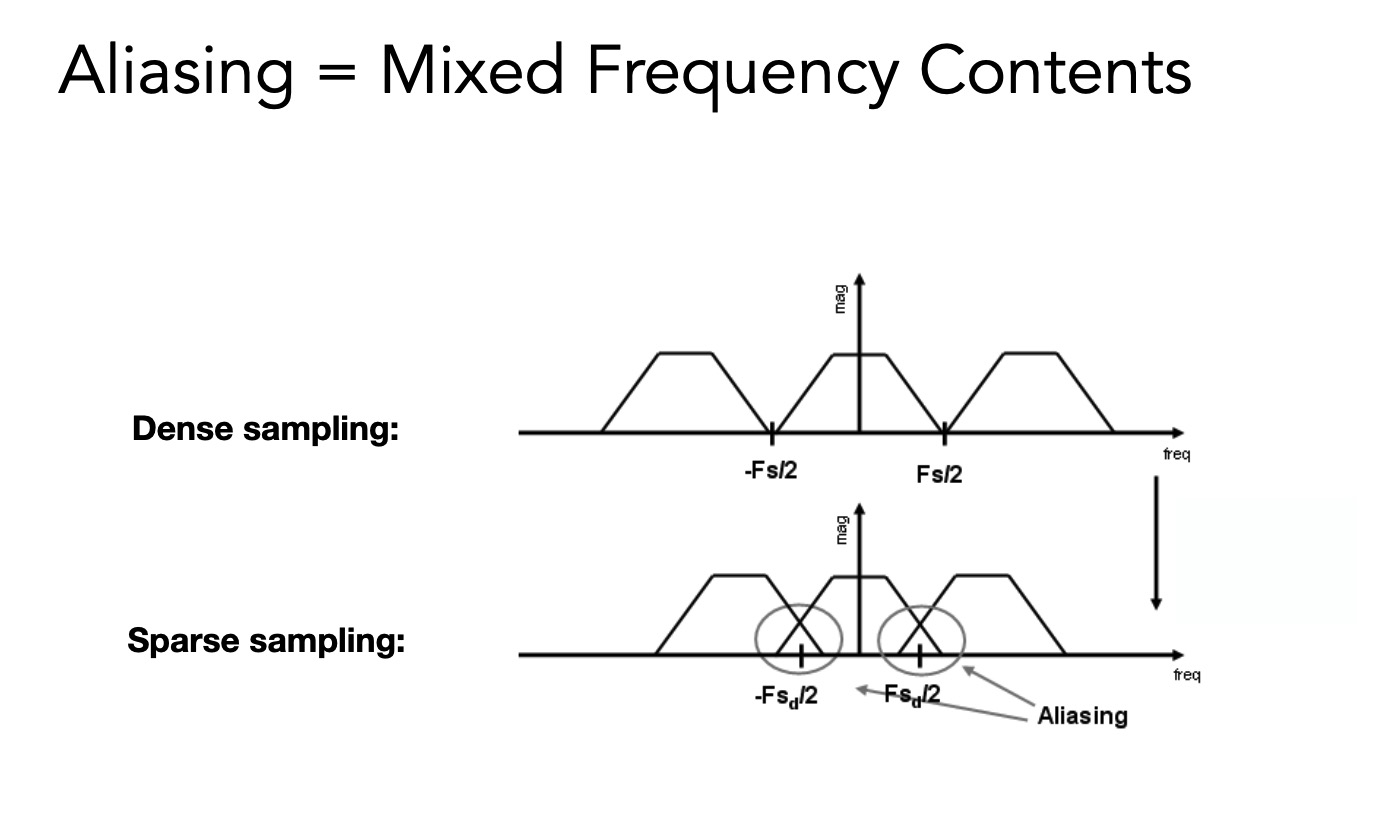
采样频率不够 采样时间间隔越大 那么频谱间隔越小 (时域和频域有很多相反的关系)
由于频域之间间隔越小, 导致频域发生混叠, 因此产生了走样
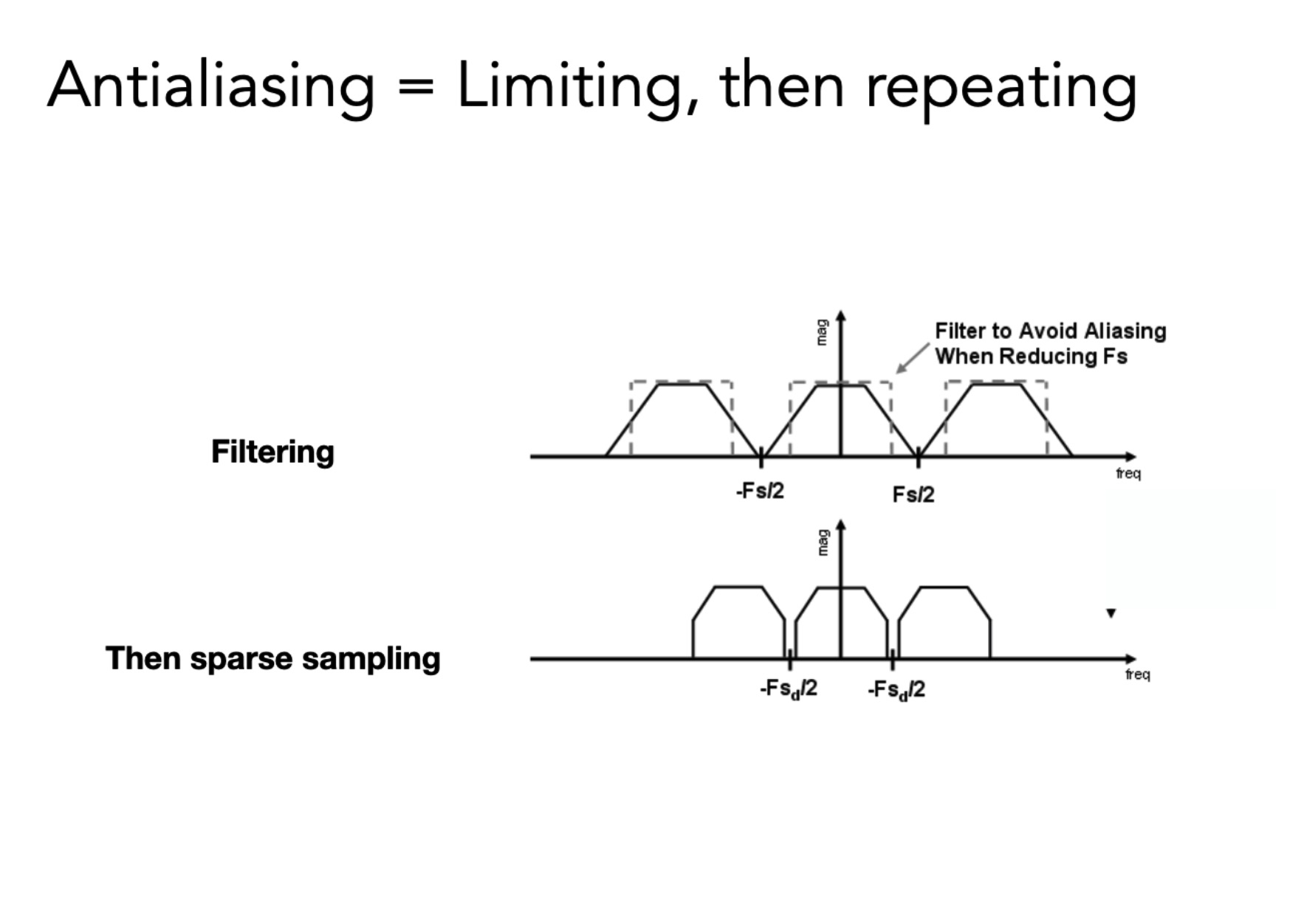
先用低通滤波, 去掉高频信息, (模糊), 然后再采样
下面做的就是去掉高频信号 之后还是以原来的采样率去采样, 去掉高频之后就不再发生混叠了
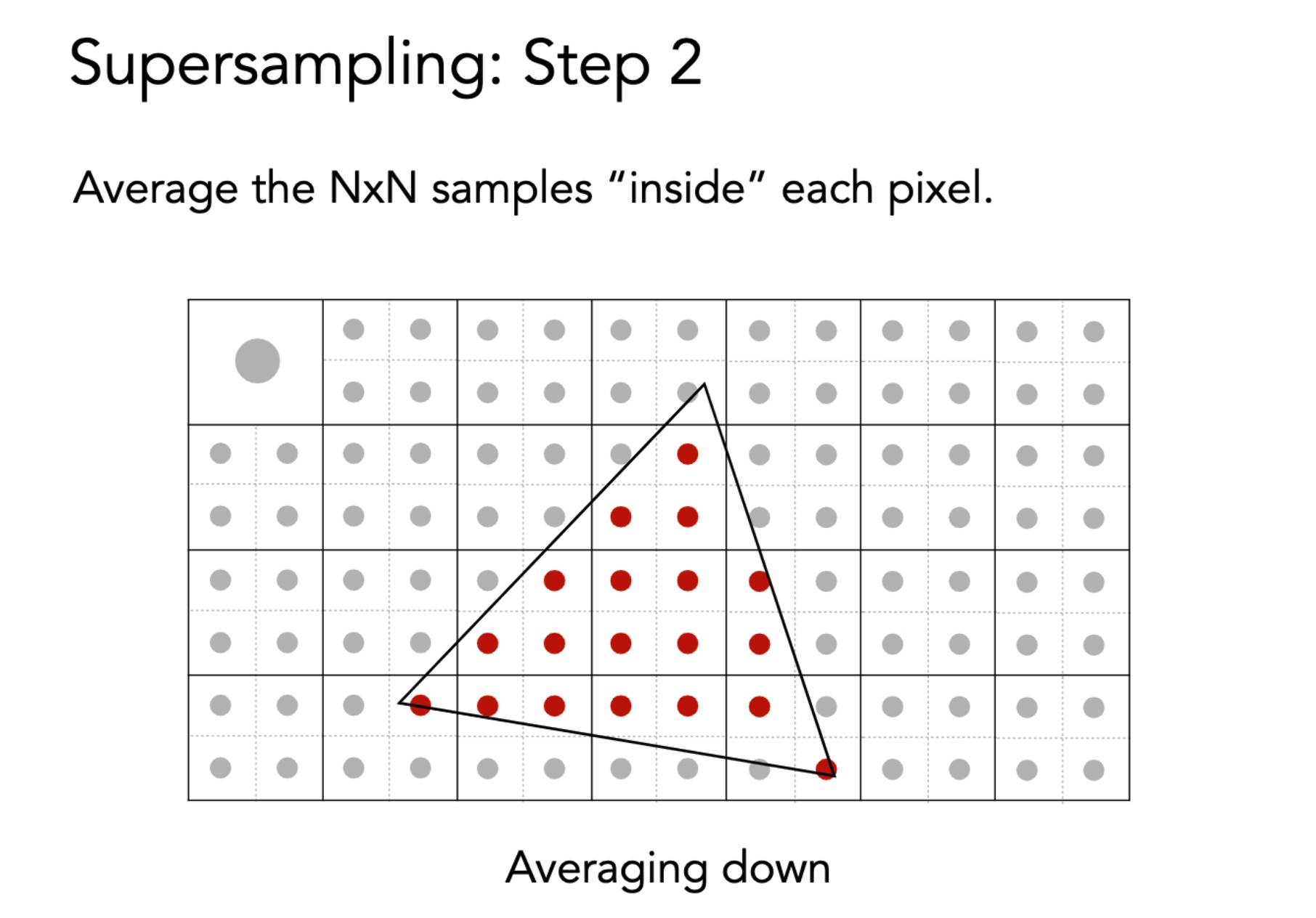
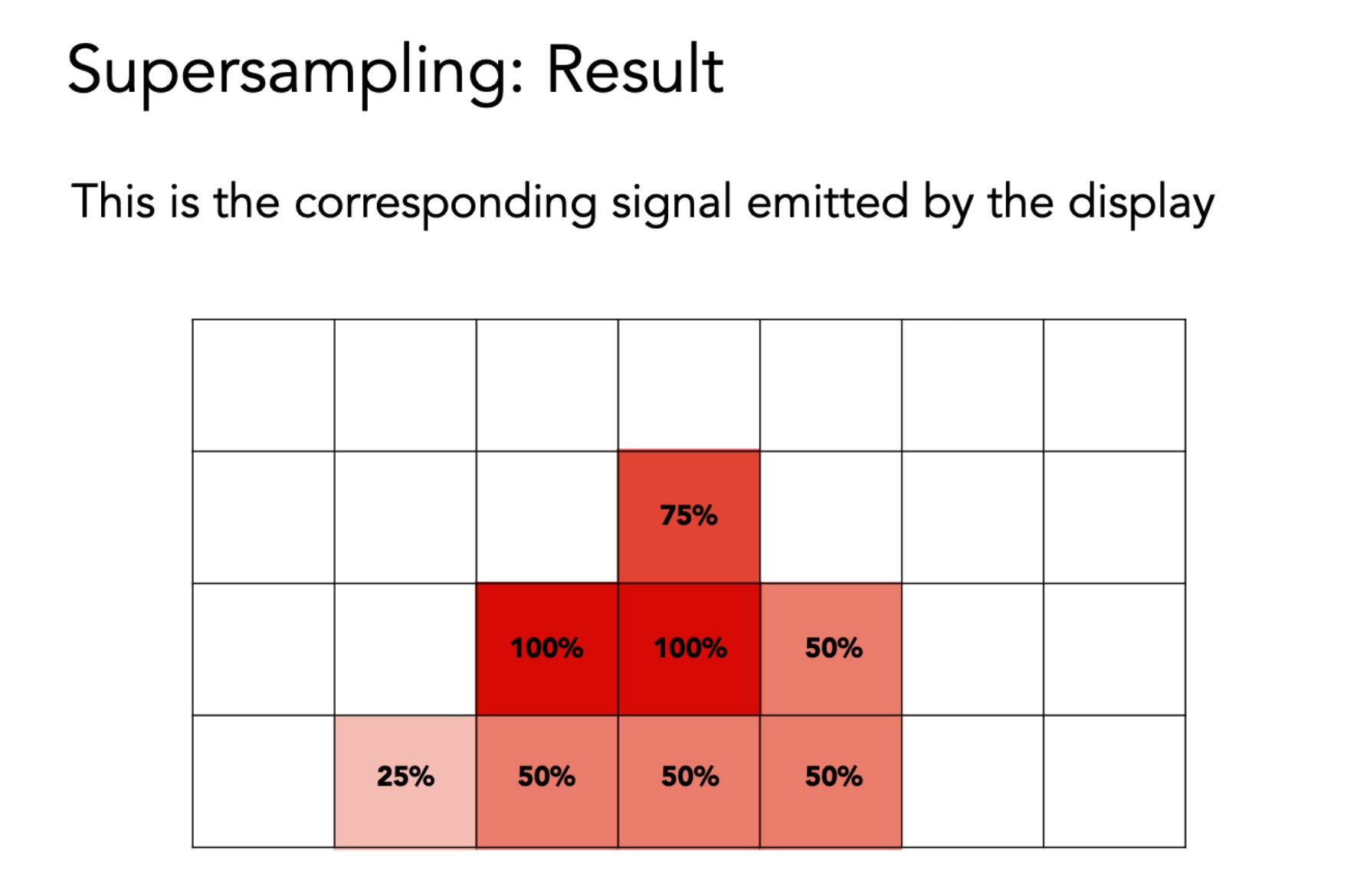
超采样, 每一个像素都再次划分, 然后判断点是否在三角形内, 之后再做平均 (这样去做的模糊).
PS 超采样并没有增加分辨率