logistic_regression_ef_glm.md

লজিস্টিক রিগ্রেশন : এক্সপোনেনশিয়াল ফ্যামিলি ও জেনারালাইজড লিনিয়ার মডেল

আজকের অধ্যায়টি একটু বেশি পরিমাণ থিওরেটিক্যাল হবে। সব টপিক আলোচনাশেষে পাইথন ও পরবর্তীতে টেনসরফ্লোতে ইম্প্লিমেন্ট করে দেখানো হবে।

টপিক

• এক্সপোনেনশিয়াল ফ্যামিলি
• জেনারালাইজড লিনিয়ার মডেল, কন্সট্রাকশন ও অ্যাজাম্পশন
• জেনেরালাইজড মডেল থেকে লজিস্টিক রিগ্রেশন

গত অধ্যায়ে আমরা লজিস্টিক রিগ্রেশন, বার্নুলি ট্রায়াল ও বার্নুলি ডিস্ট্রিবিউশনের সাথে পরিচিত হয়েছি। মূল বিষয় হচ্ছে, বার্নুলি ডিস্ট্রিবিউশনের সাথে লজিস্টিক রিগ্রেশনের সম্পর্ক কোথায়? লাইকলিহুড আর ম্যাক্সিমাম লাইকলিহুড কী জিনিস?

---

এইসব বিষয় বোঝার জন্য আমাদের কিছু প্রিরিকুইজ্যিট জ্ঞান লাগবে, প্রথমত আসা যাক এক্সপোনেনশিয়াল ফ্যামিলির ব্যাপারে (Exponential Family)।

এক্সপোনেনশিয়াল ফ্যামিলি (Exponential Family)

Generalized Linear Model তৈরি করার আগে এক্সপোনেনশিয়াল ফ্যামিলির ডিস্ট্রিবিউশন সম্পর্কে পরিষ্কার ধারণা থাকতে হবে।

একটা নির্দিষ্ট ধরণের ডিস্ট্রিবিউশন দের একত্রে Exponential Family বলা হয় যদি নিচের সমীকরণ সেই ডিস্ট্রিবিউশন মেনে চলে। অপর কথায়, আমরা অনেক ধরণের প্রব্যাবিলিটি ডিস্ট্রিবিউশনের সাথে পরিচিত, যেমন বার্নুলি, পয়জন, গাউসিয়ান ইত্যাদি। এদেরকে যদি একটা সাধারণ (Common) সমীকরণ দ্বারা প্রকাশ করা যায় তাহলে আমরা তাদেরকে বলব এক্সপোনেনশিয়াল ফ্যামিলি।

সমীকরণটি হল, $$ p(y;\eta) = b(y) \exp \left( \eta^{T} T(y) - a(\eta) \right) $$ যেখানে, $$ \begin{align} \eta &= Natural , (Canonical) , Parameter \ T(y) &= Sufficient , Statistic \ a(\eta) &= Log , Partition , Function \ e^{a(\eta)} &= Normalizing , Constant \end{align} $$ কিছু বইতে (PRML by Bishop) এভাবেও লিখে থাকে, $$ p(\textbf{x}|\eta) = h(\textbf{x}) g(\eta) \exp { \eta^{T}\textbf{u}(\textbf{x}) } $$ কিছু ক্ষেত্রে এই নোটেশন একটু মিসলিডিং, আমরা সাধারণত ইনপুট কে $$\textbf{x}$$ বলে থাকি। এখানে প্যারামিটার $$\eta$$ এবং আউটপুট কিন্তু $$\textbf{x}$$ । $$\eta^{T}$$ দেয়ার কারণ হল, যদি ম্যাট্রিক্স ফর্ম হয় তাহলে $$\eta$$ কে ট্রান্সপোজ করে $$T(y)$$ এর ডট প্রোডাক্ট নেয়া হবে।

একই পরিবারের বিভিন্ন ডিস্ট্রিবিউশন কীভাবে ডিফাইন করা হয়

$$T, a, b$$ এই তিনটি প্যারামিটার যদি আমরা ফিক্সড রাখি, এবং $$\eta$$ কে পরিবর্তিত করতে থাকি, তাহলে আমরা একই পরিবারের বিভিন্ন ডিস্ট্রিবিউশন পাব।

যেমন,

বার্নুলি ডিস্ট্রিবিউশন এক্সপোনেনশিয়াল পরিবারের সদস্য (প্রমাণ দ্রষ্টব্য)। এই ডিস্ট্রিবিউশনের নির্দিষ্ট $$T, a, b$$ রয়েছে, আমরা যদি এর $$\eta$$ এর পরিবর্তন করি তাহলে নিচের গ্রাফগুলো পাব।

import seaborn as sns
import matplotlib.pyplot as plt
import scipy

plt.figure(figsize=(8, 6))

eta = 0.25

N = 10 # Number of Samples

samples = scipy.linspace(0,10,11) 

pmf = scipy.stats.binom.pmf(samples, N, eta)

sns.barplot(samples, pmf)

আউটপুট

$$\eta=0.5$$ করলে,

$$\eta=0.9$$ করলে,

এক্সপোনেনশিয়াল ডিস্ট্রিবিউশন ফ্যামিলির সদস্য কারা?

সাধারণত আমরা যেসব প্রব্যাবিলিটি ডিস্ট্রিবিউশন নিয়ে কাজ করি সবাই কমবেশি এক্সপোনেনশিয়াল ডিস্ট্রিবিউশন পরিবারের সদস্য। যেমন,

• নরমাল (Normal)
• এক্সপোনেনশিয়াল (Exponential)
• গামা (Gamma)
• কাই-স্কয়ার্ড (Chi-squared)
• বিটা (Beta)
• ডিরিশ্লে (Dirichlet)
• বার্নুলি (Bernoulli)
• ক্যাটেগরিকাল (Categorical)
• পয়সন (Poisson)
• উইশার্ট (Wishart)
• ইনভার্স উইশার্ট (Inverse Wishart)

প্রমাণ কী এরা এক্সপোনেনশিয়াল ডিস্ট্রিবিউশন ফ্যামিলির সদস্য?

আমরা যদি প্রতিটা ডিস্ট্রিবিউশনের সমীকরণকে এক্সপোনেনশিয়াল ফ্যামিলির সাধারণ সমীকরণ আকারে প্রকাশ করতে পারি তাহলেই বুঝব এই ডিস্ট্রিবিউশনগুলো ওই পরিবারের সদস্য।

১. বার্নুলি ডিস্ট্রিবিউশন এর প্রমাণ

$$p(y;\phi) = $$ [$$y$$ হওয়ার সম্ভাবনা কত যদি $$\phi$$ দেয়া থাকে (দেয়া থাকে কথাটা ভুল, ধরে নিতে হবে $$y$$ যদি $$\phi$$ দ্বারা নিয়ন্ত্রিত হয়) ] $$ \begin{align} p(y;\phi) &= \phi^{y}(1-\phi)^{1-y} \ &= \exp \left[ \ln{ \phi^{y}(1-\phi)^{1-y} } \right] \ &= \exp \left[ \ln{ \phi^{y} } + \ln { (1-\phi)^{1-y} } \right] \ &= \exp[y \ln \phi + (1-y) \ln (1-\phi)] \ &= \exp [y \ln \phi + \ln(1-\phi) - y\ln(1-\phi)] \ &= \exp\left [\left( \ln \frac{\phi}{1-\phi} \right)y + \ln(1-\phi) \right] \end{align} $$ এক্সপোনেনশিয়াল ফ্যামিলির সমীকরণ, $$ p(y;\eta) = b(y) \exp \left( \eta^{T} T(y) - a(\eta) \right) $$ সমীকরণ দুইটা তুলনা করে,

ন্যাচারাল প্যারামিটার $$\eta$$ ও ডিস্ট্রিবিউশনের প্যারামিটারের $$\phi$$ সাথে সম্পর্ক $$ \begin{align} \eta&=\ln \frac{ \phi} {1-\phi} \ e^{\eta} &= \frac{\phi}{1-\phi} \ e^{-\eta} &= \frac{1-\phi}{\phi} \ e^{-\eta} &= \phi^{-1} - 1 \ \phi &=\frac{1}{1 + e^{-\eta}} \end{align} $$ তাহলে, $$ \begin{align} T(y) &= y \ a(\eta) &= - \ln(1-\phi) \ &= \ln (1 + e^{\eta}) \ b(y) &= 1 \end{align} $$ যেহেতু বার্নুলি ডিস্ট্রিবিউশনকে এক্সপোনেনশিয়াল ফ্যামিলির সাধারণ সমীকরণ দ্বারা প্রকাশ করা গিয়েছে তাই বার্নুলি ডিস্ট্রিবিউশন এক্সপোনেনশিয়াল পরিবারের একজন সদস্য!

২. নরমাল ডিস্ট্রিবিউশন বা গাউসিয়ান ডিস্ট্রিবিউশন

এখানে সিঙ্গেল ডিমেনশনাল বা 1D গাউসিয়ান ডিস্ট্রিবিউশনের কথা চিন্তা করব। এবং ভ্যারিয়েবলের সংখ্যা কমানোর জন্য ধরে নিচ্ছি $$\sigma^{2}=1$$।

Mean ও Variance সহ গাউসিয়ান ডিস্ট্রিবিউশন, $$ p(y ; \mu, \sigma^{2}) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\left( - \frac{(y-\mu)^{2}}{2\sigma^{2}} \right) $$ সেক্ষেত্রে গাউসিয়ান ডিস্ট্রিবিউশন লেখা যাবে এভাবে, $$ \begin{align} p(y;\mu) &= \frac{1}{\sqrt{2\pi}} \exp \left( -\frac{1}{2} (y-\mu)^{2} \right) \ &= \frac{1}{\sqrt{2\pi}} \exp \left( -\frac{1}{2} (y^{2} - 2y\mu + \mu^{2} ) \right) \ &= \frac{1}{\sqrt{2\pi}} \exp \left( -\frac{1}{2} y^{2} \right) . \exp \left( \mu y - \frac{1}{2} \mu^{2} \right) \end{align} $$ তুলনা করে, $$ \begin{align} \eta &= \mu \ T(y) &= y \ a(\eta) &= \frac{\mu^{2}}{2} \ &= \frac{\eta^{2}}{2} \ b(y) &= \frac{1}{\sqrt{2\pi}} \exp\left( -\frac{y^{2}}{2} \right) \end{align} $$ এভাবে বাকি ডিস্ট্রিবিউশনের জন্যও প্রমাণ করা যাবে।

জেনেরালাইজড লিনিয়ার মডেল (Generalized Linear Model) অ্যাজাম্পশন

এতক্ষণ ধরে আমরা চিন্তা করছিলাম, আউটপুটের উপরে তার প্রব্যাবিলিটি ডিস্ট্রিবিউশন কিরকম হয়। কিন্তু আউটপুট কোন ডিস্ট্রিবিউশন আসবে সেটা যখন ঠিক হয়ে যায় তখন আমাদের ইনপুট ফিচার $$\textbf{x}$$ এর সাথে আউটপুট $$y$$ এর একটা সম্পর্ক স্থাপন করতে হয়।

আমাদের আপাতত লক্ষ্য একটা লিনিয়ার মডেলের সাথে আউটপুটের সম্পর্ক স্থাপন করা এবং এটা করার জন্য আমাদের কিছু Assume করে নিতে হবে। সেগুলো হল,

1. আমরা যে সমস্যা নিয়ে বিবেচনা করছি তার আউটপুট $$y$$ অবশ্যই কোন একটি এক্সপোনেনশিয়াল ফ্যামিলির PDF (Probability Distribution Function) থেকে জেনারেটেড হতে হবে। ম্যাথেমেটিক্যালি, $$y | x; \theta \sim \textbf{ExponentialFamily}(\eta)$$ , এটার মানে হচ্ছে $$y$$ হল আউটপুট, $$x$$ হল ইনপুট এবং $$\theta$$ হল সেই প্যারামিটার যার মান এস্টিমেট করতে হবে এবং $$\textbf{ExponentialFamily}$$ এর সদস্যের ক্যানোনিক্যাল বা ন্যাচারাল প্যারামিটার হবে $$\eta$$ । আমরা সবসময়ই কিন্তু $$\eta$$ এবং $$\theta$$ এর সাথে সম্পর্ক স্থাপন করতে পারি। এতে সুবিধা হল, আমরা যদি $$\theta$$ এর মান পেয়ে যাই অর্থাৎ আমরা জানব কোন $$\eta$$ এর জন্য ওই PDF টা আমাদের ডেটাসেট এর সাথে ফিট করে। আরও সাধারণভাবে বলা যেতে পারে, $$\theta$$ এর মান পাওয়া গেলে $$\eta$$ এর মান পাব এবং ওই $$\eta$$ ব্যবহার করে একটা ডিস্ট্রিবিউশন প্লট তৈরি করতে পারব যেটা দিয়ে পরবর্তীতে প্রেডিকশন করা যাবে। কারণ PDF এর কাজই হচ্ছে ইনপুটে কোন মান নিয়ে আউটপুট একটা নির্দিষ্ট মান হওয়ার সাম্ভাব্যতা কত সেটা বের করা।
2. এবার যদি $$x$$ দেয়া থাকে, তাহলে আমাদের $$T(y)$$ এর মান বের করতে হবে সাধারণত যেটা $$T(y)=y$$ হয়ে থাকে। অর্থাৎ, আমাদের হাইপোথিসিস হবে এক্সপেক্টেড মানের সমান $$h_{\theta}(x) = E[y|x]$$।
3. এক্সপেক্টেড মান : বাইনোমিয়াল ডিস্ট্রিবিউশন হল বার্নুলি ডিস্ট্রিবিউশনের $$n$$ সংখ্যক ট্রায়াল। কয়েন টসের কথা চিন্তা করা যাক, হেড কে আমরা $$1$$ ও টেইলকে যদি $$0$$ দ্বারা প্রকাশ করি। তাহলে Fair Coin এর ক্ষেত্রে প্রতি আউটকাম হওয়ার সম্ভাবনা $$\phi = \frac{1}{2}$$ । তাহলে, $$E[X=1]= \phi = (1 - 0) \times \frac{1}{2} + (1 - 1)\times \frac{1}{2} = \frac{1}{2} $$ ।
4. বার্নুলি ডিস্ট্রিবিউশনের এক্সপেক্টেড মানের সাধারণ সমীকরণ: হাইপোথিসিসে যদি ফিচার $$x$$ দেয়া হয় এবং ফাংশনটি $$\theta$$ প্যারামিটার দ্বারা ডিফাইন করা হয় তাহলে $$y=1$$ হওয়ার সম্ভাবনা বা Expected Value $$h_{\theta}(x) = p(y=1 | x; \theta) = 0 . p(y = 0 | x; \theta) + 1 . p(y=1 | x; \theta) = \phi$$
5. এটা একটু উদ্ভট রকমের অ্যাজাম্পশজন। আমাদের ডিস্ট্রিবিউশনের প্যারামিটার $$\theta$$ , ইনপুট $$x$$ এবং ডিস্ট্রিবিউশনের ক্যানোনিক্যাল প্যারামিটার $$\eta$$ এর সাথে সম্পর্ক স্থাপন করতে হবে। আমরা অলরেডি $$\theta$$ এবং $$\eta$$ এর সম্পর্ক ডিস্ট্রিবিউশন থেকে বের করতে পারি। কিন্তু $$x$$ এর সাথে সম্পর্ক কীভাবে স্থাপন করা যায়? তাই আমাদের ধরে নিতে হবে, $$\eta$$ এর সাথে $$\theta$$ এবং ইনপুট $$x$$ এর সম্পর্ক লিনিয়ার। বা, $$\eta = \sum_{i}^{n}\theta_{i}x_{i}$$ , যেখানে $$n$$ হল নাম্বার অফ ফিচার বা কলাম সংখ্যা। ভেক্টরাইজড বা ম্যাট্রিক্স আকারে এভাবে লেখা যায় $$\eta = \Theta^{T} \textbf{x}$$ । যেহেতু আমরা ধরেই নিয়েছি মডেলটা লিনিয়ার তাই ডিস্ট্রিবিউশনের প্যারামিটারের সাথে এর সম্পর্ক লিনিয়ার থাকাটাই যুক্তিযুক্ত।

লজিস্টিক রিগ্রেশনের ক্ষেত্রে GLM কনস্ট্রাকশন

লজিস্টিক রিগ্রেশনে আউটপুট বাইনারি হয় এবং আমরা জানি এই ডিস্ট্রিবিউশনের আউটপুট সেট এভাবে লেখা যায়, $$y \in {0, 1}$$। আউটপুট কী হবে সেটার উপর ভিত্তি করে PDF বাছাই করা হয়, আউটপুট এখানে বাইনারি তাই, বার্নুলি ডিস্ট্রিবিউশন নেয়াটাই যৌক্তিক।

এবার স্টেপ বাই স্টেপ আমাদের অ্যাজাম্পশন গুলো একে একে প্রয়োগ করব।

1. আউটপুট এক্সপোনেনশিয়াল ফ্যামিলির অন্তর্গত তাই আমরা নিচের সমীকরণ গুলো অ্যাপ্লাই করতে পারব।
   1. $$\phi= \frac{1}{1+ e^{-\eta}}$$
   2. $$y|x;\theta \sim \text{Bernoulli}(\phi)$$ হলে, এই ডিস্ট্রিবিউশনের এক্সপেক্টেড ভ্যালু, $$E[y|x;\theta] = \phi = \frac{1}{1+ e^{-\eta}}$$
2. হাইপোথিসিস ফাংশন ও আউটপুটের সাথে সম্পর্ক, $$h_{\theta}(x)=E[y|x;\theta] = 1 . p(y=1|x;\theta) + 0.p(y=0 | x;\theta) = \phi$$
3. আবার লিনিয়ার সম্পর্কের অ্যাজাম্পশন থেকে, $$\eta = \theta^{T}x$$

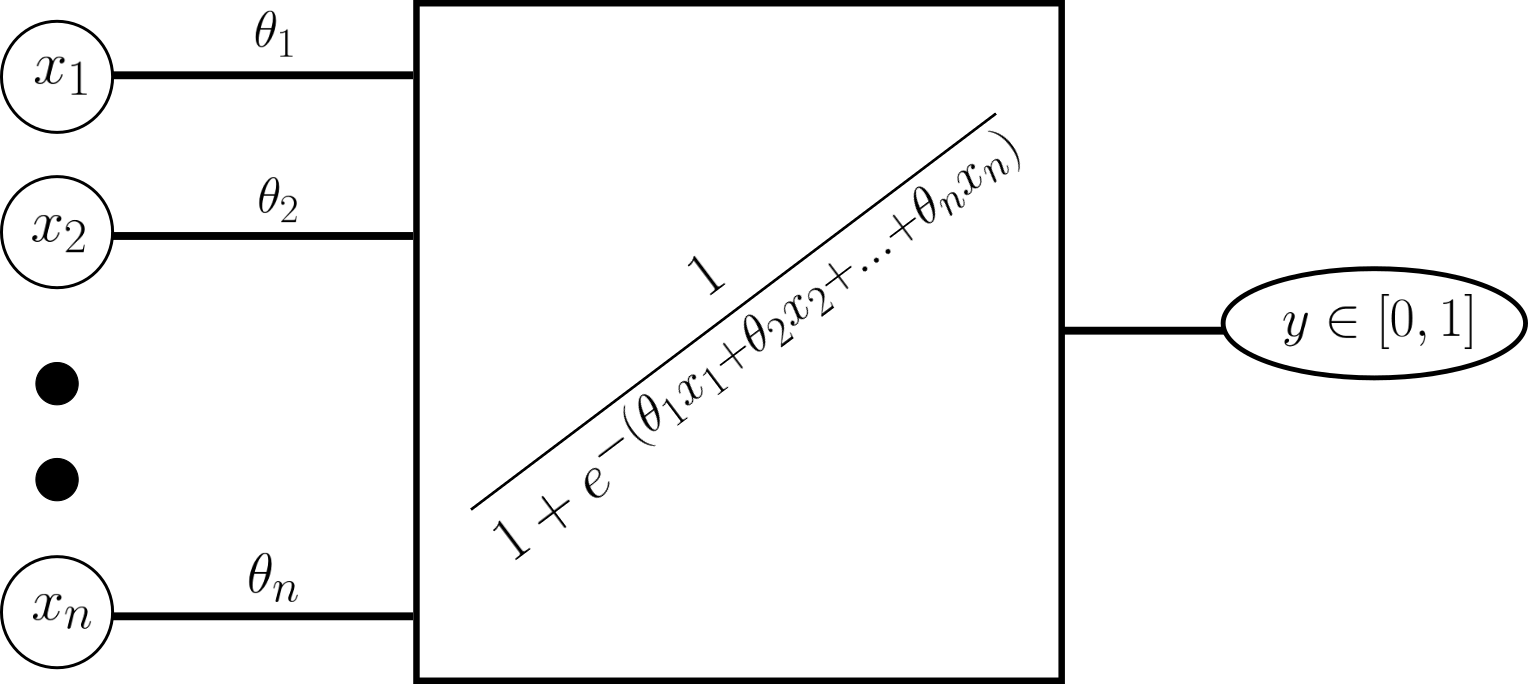
সুতরাং, $$ \begin{align} h_{\theta}(x) &= E[y|x;\theta] \ &= \phi \ &= \frac{1}{1 + e^{-\eta}} \ &= \frac{1}{1 + e^{-\theta^{T}x}} \end{align} $$ এটাই হল লিনিয়ার মডেল দিয়ে লজিস্টিক রিগ্রেশন চালানোর সূত্র! যেখানে $$\theta$$ এর মান গুলো বের করতে হবে ইনপুট $$x$$ এর সাপেক্ষে, লিনিয়ার রিগ্রেশনের মতই তবে লস ফাংশনটা হবে একটু আলাদা।

চিত্র

পরবর্তী অধ্যায়ে আমরা ক্লাসিফিকেশন করার জন্য লস ফাংশন ডিরাইভ করব।