diff --git a/DOCS/FAQ.md b/DOCS/FAQ.md
index 874fa50..0c910b0 100644
--- a/DOCS/FAQ.md
+++ b/DOCS/FAQ.md
@@ -56,6 +56,6 @@ Despite both Python versions are not fully compatible, *GrainSizeTools script* h
This issue is produced because the size of the figures returned by the script are too large to show them inside the console using the **inline** mode. To fix this go to the Spyder menu bar and in ```Tools>Preferences>IPython console>Graphics``` find *Graphics backend* and select *Automatic*.
***Can I report bugs or submit ideas to improve the script?***
-Definitely. If you have any problem using the script please just let me know (see an email address here: http://marcoalopez.github.io/ ). Feedback from users is always welcome and important to develop a better script. Lastly, you can also create a fork of the project and develop your own tools based on the GST script since it is open source and free. Enjoy.
+Definitely. If you have any problem using the script please just let me know (see an email address here: http://marcoalopez.github.io/ ). Feedback from users is always welcome and important to develop a better script. Lastly, you can also create a fork of the project and develop your own tools based on the GST script since it is open source and free.
[table of contents](https://github.com/marcoalopez/GrainSizeTools/blob/master/DOCS/tableOfContents.md)
diff --git a/DOCS/Requirements.md b/DOCS/Requirements.md
index 9ebeea1..541ec82 100644
--- a/DOCS/Requirements.md
+++ b/DOCS/Requirements.md
@@ -3,7 +3,7 @@
Requirements
-------------
-GrainSizeTools script requires [Python][1] 2.7.x (legacy) or 3.5+ versions and the scientific libraries [*Numpy*][2], [*Scipy*][3], [*Pandas*][9] and [*Matplotlib*][4]. We recommend installing the [Anaconda distribution][5] or the [Enthought Canopy][6] distributions. Both distributions have free basic versions that include all the required the scientific packages. In case you have space problems in your hard disk, there is a distribution named [miniconda][7] that only installs the packages you actually need.
+GrainSizeTools script requires [Python][1] 2.7.x (legacy) or 3.5+ versions and the scientific libraries [*Numpy*][2], [*Scipy*][3], [*Pandas*][9] and [*Matplotlib*][4]. We recommend installing the [Anaconda][5] or the [Enthought Canopy][6] distributions. Both distributions have free basic versions that include all the required the scientific packages. In case you have space problems in your hard disk, there is a distribution named [miniconda][7] that only installs the packages you actually need.
The approach of the script is based on the estimation of the areas of the grain profiles obtained from thin sections. It is therefore necessary to measure them in advance and save the results in a txt/csv file. For this task, we highly encourage you to use the [*ImageJ*](http://rsbweb.nih.gov/ij/) application or one of their different flavours (see [here](http://fiji.sc/ImageJ)). These are public-domain image processing programs widely used for scientific research that runs on Windows, macOS, and Linux platforms. This documentation contains a quick tutorial on how to measure the areas of the grain profiles with ImageJ, see the *Table of Contents*. The combined use of **ImageJ** and **GrainSizeTools script** is intended to ensure that all data processing steps are done through free and open-source programs/scripts that run under any operating system.
diff --git a/DOCS/sourceDoc_to_pdf.md b/DOCS/sourceDoc_to_pdf.md
index 466ca43..2814855 100644
--- a/DOCS/sourceDoc_to_pdf.md
+++ b/DOCS/sourceDoc_to_pdf.md
@@ -3,10 +3,10 @@
This pdf manual is based on the online documentation at
**Manual version**:
-v30
+v31
**Release date**:
-2017/12/24
+2018/03/26
**Author**:
Marco A. Lopez-Sanchez
@@ -22,13 +22,14 @@ This document is licensed under a [Creative Commons Attribution-NonCommercial-Sh
- *Open and running the script*
- *A brief note on the organization of the script*
- *Using the script to visualize and estimate the grain size*
- - *Loading the data and extracting the areas of the grain profiles*
- - *Estimating the apparent diameters from the areas of the grain profiles*
- - *Obtaining apparent grain size measures*
- - *Estimating differential stress using piezometric relations (paleopiezometry)*
- - *Derive the actual 3D distribution of grain sizes from thin sections*
- - *Comparing different grain size populations using box plots*
- - *Other methods of interest*
+ - Loading the data and extracting the areas of the grain profiles
+ - Estimating the apparent diameters from the areas of the grain profiles
+ - Obtaining apparent grain size measures
+ - Estimating differential stress using piezometric relations (paleopiezometry)
+ - Estimating a robust confidence interval
+ - Derive the actual 3D distribution of grain sizes from thin sections
+ - Comparing different grain size populations using box plots
+ - Other methods of interest
- GST script quick tutorial
- *Loading the data and extracting the areas of the grain profiles*
- *Estimating the apparent diameters from the areas of the grain profiles*
@@ -45,9 +46,20 @@ This document is licensed under a [Creative Commons Attribution-NonCommercial-Sh
## Requirements
-GrainSizeTools script requires [Python](https://www.python.org/) 2.7.x (legacy) or 3.x versions and the scientific libraries [*Numpy*](http://www.numpy.org/), [*Scipy*](http://www.scipy.org/), [*Pandas*](http://pandas.pydata.org) and [*Matplotlib*](http://matplotlib.org/). We recommend installing the [Continuum Anaconda](https://store.continuum.io/cshop/anaconda/) or the [Enthought Canopy](https://www.enthought.com/products/canopy/) (maybe more easy-friendly for novices) distributions. Both distributions have free basic versions that already include the scientific packages named above and they also provide free academic licenses for advanced versions. In case you have space problems in your hard disk, there is a distribution named [miniconda](http://conda.pydata.org/miniconda.html) that only installs the packages you actually need.
+GrainSizeTools script requires [Python][1] 2.7.x (legacy) or 3.5+ versions and the scientific libraries [*Numpy*][2], [*Scipy*][3], [*Pandas*][9] and [*Matplotlib*][4]. We recommend installing the [Anaconda][5] or the [Enthought Canopy][6] distributions. Both distributions have free basic versions that include all the required the scientific packages. In case you have space problems in your hard disk, there is a distribution named [miniconda][7] that only installs the packages you actually need.
+
+The approach of the script is based on the estimation of the areas of the grain profiles obtained from thin sections. It is therefore necessary to measure them in advance and save the results in a txt/csv file. For this task, we highly encourage you to use the [*ImageJ*](http://rsbweb.nih.gov/ij/) application or one of their different flavours (see [here](http://fiji.sc/ImageJ)). These are public-domain image processing programs widely used for scientific research that runs on Windows, macOS, and Linux platforms. This documentation contains a quick tutorial on how to measure the areas of the grain profiles with ImageJ, see the *Table of Contents*. The combined use of **ImageJ** and **GrainSizeTools script** is intended to ensure that all data processing steps are done through free and open-source programs/scripts that run under any operating system.
+
+[1]: https://www.python.org/
+[2]: http://www.numpy.org/
+[3]: http://www.scipy.org/
+[4]: http://matplotlib.org/
+[5]: https://www.anaconda.com/download/
+[6]: https://www.enthought.com/products/canopy/
+[7]: http://conda.pydata.org/miniconda.html
+[8]: http://rsbweb.nih.gov/ij/
+[9]: http://pandas.pydata.org
-The approach of the script is based on the estimation of the areas of the grain profiles obtained from thin sections. It is therefore necessary to measure them in advance and save the results in a txt/csv file. For this task, we highly encourage you to use the [*ImageJ*](http://rsbweb.nih.gov/ij/) application or one of their different flavours (see [here](http://fiji.sc/ImageJ)), since they are public-domain image processing programs widely used for scientific research that runs on Windows, macOS, and Linux platforms. This manual contains a quick tutorial on how to measure the areas of the grain profiles with ImageJ, see the *Table of Contents*. The combined use of **ImageJ** and the **GrainSizeTools script** is intended to ensure that all data processing steps are done through free and open-source programs/scripts that run under any operating system.
@@ -55,41 +67,53 @@ The approach of the script is based on the estimation of the areas of the grain
GrainSizeTools (GST) script is primarily targeted at anyone who wants to:
-1. Visualize grain size features
-2. Obtain a set of single 1D measures of grain size to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks or any other type of crystalline aggregate
-3. Estimate differential stress via paleopizometers (**New in version 1.4!**)
-4. Estimate the actual 3D distribution of grain sizes from a population of apparent grain sizes measured in thin sections. This includes the estimation of the volume occupied by a particular grain size fraction and the shape of the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution)
+1. Visualize the distribution of apparent grain sizes and extract different statistical parameters to describe the features of the distribution
+2. Estimate differential stress via paleopizometers (**New in versions 1.4+!**)
+3. Approximate the actual 3D distribution of grain sizes from thin sections. This includes an estimate of the volume occupied by a particular grain size fraction and the shape of the population of grain sizes (assuming that the distribution of grain sizes is lognormal-like)
-GST script requires as the input the measurement of the areas of the grain profiles (grain-by-grain) in a thin section. Hence, the script does not apply for determining mean grain sizes via the planimetric (Jeffries) (i.e. the number of grains per unit area) or intercept (the number of grains intercepted by a test line per unit length of test line) procedures. The reasons for using grain-by-grain methods over the planimetric/intercept procedures in rocks are detailed in [Lopez-Sanchez and Llana-Fúnez (2015)](http://www.solid-earth.net/6/475/2015/). The following is an overview of the key assumptions to consider so that the results obtained by the script are meaningful and reliable.
+GST script only requires as input the areas of the grain profiles measured grain-by-grain in a thin section. The script is not intended to determine the mean grain size via the planimetric (Jeffries) (i.e. the number of grains per unit area) or intercept (the number of grains intercepted by a test line per unit length of test line) methods. The reasons for using grain-by-grain methods over the planimetric or intercept ones in natural rocks are detailed in [Lopez-Sanchez and Llana-Fúnez (2015)](http://www.solid-earth.net/6/475/2015/). Below is a brief outline of the key assumptions to consider so that the results obtained by the script are meaningful and reliable.
### Safety concerns
> All this safety concerns assume that the calibration of the microscope and the scale of the micrographs were set correctly.
-#### **Getting unidimensional measures of apparent grain size**
+#### Determination of "average" (mean, median, peak) apparent grain sizes
+
+Unidimensional apparent grain size measures such as the **mean** or the **median** are only meaningful in specimens that show a **unimodal distribution of diameters** (or areas). It is therefore key to **always visualize if the distribution of apparent grain sizes is unimodal** (a single peak). In the case that the distribution is multimodal (two or more frequency peaks), you can use for comparative purposes the **location of the frequency peaks** based on the Kernel density estimate [(Lopez-Sanchez and Llana-Fúnez, 2015)](http://www.solid-earth.net/6/475/2015/). Despite this, the best option when a multimodal distribution appears is to separate the different populations of grain size using image analysis methods.
+
+Unfortunately, no general protocol exists in the earth science community on what unidimensional grain size measures to use when using grain-by-grain methods. For example, in the case of paleopiezometry studies, some authors have been using the mean, others the median and some the mode. In addition, some authors applied stereological corrections and others do not, and some estimate the logarithmic or the square root grain size instead of the linear grain size. Since it seems this is not going to change in the short term, it is advisable to always report all the different unidimensional grain size measures (mean, median, freq. peak). This will allow other scientists to directly compare their data with yours without using correction factors which always involve some assumptions. In any event, you will have to choose one of them in your study so we advise from here to follow this rule of thumb:
+
+- use **mean and standard deviation (SD)** when your **distribution is normal-like**
+- use **median and interquartile (or interprecentil) range** when your **distribution is skewed**
+
+The rationale behind this rule is that the sample mean is generally more efficient than the median, but the sample median is always more robust. The latter feature makes the median more efficient when distributions have "thick" tails as it happens in most skewed distributions.
+
+When grains are equant (equiaxed) or near-equant (i.e. aspect ratios mostly < 2.0) any specimen orientation is acceptable for estimating unimodal grain size measures, and a **single section** could be enough to obtain a reliable estimate as long as you measure a minimum of grain sections (see below for details). When grains show aspect ratios above 2.0 and preferred orientation throughout the rock volume, you will need to **estimate the grain size over three orthogonal sections and then average the results** to obtain meaningful results. Although specimens with equant grains accept any orientation to estimate unidimensional grain size measures, it is advisable to use a principal section. Specifically, we promote the use of the XZ section, i.e. parallel to the lineation and perpendicular to the foliation, since this will allow us: (i) to estimate whether the grains are far from equant using the aspect ratio; and (ii) to provide a fairer comparison between different specimens when near-equant grains and preferred orientation of the large axes exist.
-Unidimensional apparent grain size measures such as the **mean** or **median** are only meaningful in specimens that show a **unimodal distribution of diameters** (or areas). Consequently, in all cases it is key to visualize the distribution of apparent grain sizes and **observe if the distribution is unimodal** (a single peak). In the case that the distribution is multimodal (two or more peaks), you can use for comparative purposes the modal interval or, better, the **location of frequency peaks** based on the Kernel density estimate [(Lopez-Sanchez and Llana-Fúnez, 2015)](http://www.solid-earth.net/6/475/2015/). Despite this, the best option when a multimodal grain size distribution occurs is to separate the different populations of grain size previously via image analysis methods. Unfortunately, no general protocol exists in the earth science community for unidimensional grain size measures. Consequently, if possible, it is advisable to always report all the different unidimensional grain size measures (mean, median, freq. peak). This will allow other scientists to compare their data with yours directly when using a different type of grain size measurement from that used in your study.
+To obtain reliable grain size estimates you should measure (or your grain boundary map should contain) at least 433 grain sections, although use better 965 sections when possible. This sample size will ensure that 95 % of the time the mean grain size estimated will have an error equal or less than ± 4 % (99% if you measure 965) (see [Lopez-Sanchez and Llana-Fúnez, 2015](http://www.solid-earth.net/6/475/2015/) for details). If you want to obtain an accurate **confidence interval** for your estimates you have to take several representative micrographs from the same specimen (three or more) and estimate the "average" (mean, median or peak) grain size in each of them. Then use the ```confidence_interval``` function implemented in the script to get a robust confidence interval. For details on how this determination works see the next section or the documentation of the function using the command ``help(confidence_interval)`` in the console.
-When we estimate unimodal grain size measures from a **single section**, whatever the number of grain boundary maps used, the results will be only meaningful if grains are equant (equiaxed) or near-equant (i.e. aspect ratios mostly < 2.0). If grains systematically show aspect ratios above 2.0 and a shape preferred orientation of their large axes throughout the rock volume, you will need to **estimate the grain size over three orthogonal sections and then averaged the results**. Although specimens with equant grains accept any orientation to obtain a unidimensional grain size measure, it is advisable to use a principal section. Specifically, we promote the use of the XZ section, i.e. parallel to the lineation and perpendicular to the foliation, since this will allow us: (i) to visualize and measure whether the grains are far from equant via the aspect ratio; and (ii) to provide a fairer comparison between different specimens when near-equant grains and preferred orientation of the large axes exist.
+Regarding paleopizometry estimates, **do not use central measures derived from distributions estimated via stereological methods but directly apparent grain size measures**. The rationale for this is that stereological methods are always built on several (ill-conditioned) geometric assumptions and the results will always be, at best, only approximate. This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data.
-A common way to estimate a **confidence interval** of your grain size measurement is to take several representative micrographs from the same specimen (three or more) and then estimate the mean and the variation in the results reporting the standard deviation (SD) at a 2-sigma level of confidence, i.e. the confidence interval will be the mean ± two times the SD. To minimize variations in the results due to an insufficient number of grain measurements, a minimum of 433 (although use better 965) is required for each grain boundary map (see [Lopez-Sanchez and Llana-Fúnez, 2015)](http://www.solid-earth.net/6/475/2015/) for details).
+#### Determination of stress via paleopiezometers
-For paleopizometry/wattmetry studies **do not report measures derived from distributions estimated via stereological methods but apparent grain size measures**. The reasoning behind this is that stereological methods are built on several (weak) geometric assumptions and the results will always be, at best, only approximate. This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. Lastly, when using a piezometer relation is of paramount importance to ensure what type of grain size measure should be used. For example, if you want to use the piezometric relation established for quartz in Stipp and Tullis (2003), note that they have been established using the **root mean square apparent diameter** not the *linear nor the logarithmic mean diameter*. For details see the step-by-step tutorial.
+When using a piezometer relation is of paramount importance to ensure what type of grain size measure should be used. For example, if you want to use the piezometric relation established for quartz in Stipp and Tullis (2003), note that they have been established using the **root mean square apparent diameter** instead of the *linear or the logarithmic mean diameter*. For more details see the step-by-step tutorial.
-#### **Getting the shape of actual grain size distribution or the volume occupied by a particular grain size fraction**
+You should always estimate a **confidence interval** for your paleopiezometry estimates, which means that you should do at least three or more independent measures (i.e. from different grain size maps). Since version 1.4.4, the GST script implements a function **to estimate robust confidence intervals using the student's t-distribution** (see the step-by-step tutorial for details). This is a much robust approach than using the mean plus two times the standard deviation when the sample size is small (< 10) and both, the mean and the SD, cannot be estimated accurately.
-Estimating the actual grain size distribution from thin sections using stereological methods requires spatial homogeneity and that **grains under study are equant or near-equant**. The Saltykov and two-step methods will not provide reliable results if most of the grains show aspect ratios above 2.0, regardless of whether a shape preference orientation exists or not. In any event, this assumption is acceptable most of the time for some of the most common dynamically recrystallized non-tabular grains in crustal and mantle shear zones, such as quartz, feldspar, olivine and calcite, as well as in ice or metals/alloys. However, be careful when recrystallized grains show very irregular/lobate grain boundaries (i.e. the main recrystallization mechanism was "fast" grain boundary migration).
+#### Getting the shape of actual grain size distribution or the volume occupied by a particular grain size fraction
-The Saltykov method is suitable to estimate the volume of a particular grain fraction of interest (in percentage) and to visualize the aspect of the derived 3D grain size distribution using the histogram and a volume-weighted cumulative frequency curve. To provide reliable results, the method requires using a few number of classes and a large number of individual grain measurements. *Practical experience* indicates using more than 1000 grains and less than 20 classes. The number of classes has to be set by a trial and error approach. This will inevitably lead to different authors using a different number of classes across studies. Due to this, when estimating the volume of a grain size fraction based on a single grain boundary map it is necessary to take an absolute error of ± 5 to stay safe (see details in [Lopez-Sanchez and Llana-Fúnez, 2016](http://www.sciencedirect.com/science/article/pii/S0191814116301778)). If possible, take more than one representative grain boundary map and then estimate a confidence interval as explained above in this section.
+Estimating the actual grain size distribution from thin sections using stereological methods requires assuming spatial homogeneity and that **grains under study are equant or near-equant**. The Saltykov and two-step methods will not provide reliable results if most of the grains show aspect ratios above 2.0, regardless of whether a shape preference orientation exists or not. In any event, this assumption is acceptable most of the time for the most common *recrystallized (dynamically or statically)* mineral phases in crustal and mantle shear zones, such as quartz, feldspar, olivine, and calcite, as well as in ice or metals/alloys. However, be careful when recrystallized grains show very irregular/lobate grain boundaries (i.e. the main recrystallization mechanism was "fast" grain boundary migration).
-The two-step method ([Lopez-Sanchez and Llana-Fúnez, 2016](http://www.sciencedirect.com/science/article/pii/S0191814116301778)) is suitable for describing quantitatively the shape of the actual 3D grain size distribution using a single parameter; the multiplicative standard deviation (MSD) value. The method also provides a reliable uncertainty value. The method assumes that the actual grain size distribution follows a lognormal distribution, **there is therefore critical to visualize the distribution using the Saltykov method first and ensure that the distribution is unimodal and lognormal-like**. The MSD estimate is independent of the chosen number of classes as long as the Saltykov method produces stable results (i.e. you do not lose the lognormal appearance of the distribution due to the use of an excessive number of classes).
+The Saltykov method is suitable to estimate the volume of a particular grain fraction of interest (in percentage) and to visualize the aspect of the derived 3D grain size distribution using the histogram and a volume-weighted cumulative frequency curve. To provide reliable results, the method requires using a few numbers of classes and a large number of individual grain measurements. Practical experience indicates using more than 1000 grains and less than 20 classes. The number of classes has to be set by a trial and error approach. This will inevitably lead to different authors using a different number of classes across studies. Due to this, when estimating the volume of a grain size fraction based on a single grain boundary map it is necessary to take an absolute error of ± 5 to stay safe (see details in [Lopez-Sanchez and Llana-Fúnez, 2016](http://www.sciencedirect.com/science/article/pii/S0191814116301778)). If possible, take more than one representative grain boundary map and then estimate a confidence interval as explained above in this section.
+
+The two-step method ([Lopez-Sanchez and Llana-Fúnez, 2016](http://www.sciencedirect.com/science/article/pii/S0191814116301778)) is suitable for describing quantitatively the shape of the actual 3D grain size distribution using a single parameter called the multiplicative standard deviation (MSD) value. The method assumes that the actual grain size distribution follows a lognormal distribution, **there is therefore critical to visualize the distribution using the Saltykov method first and ensure that the distribution is unimodal and lognormal-like**. The MSD estimate is independent of the chosen number of classes as long as the Saltykov method produces stable results (i.e. you do not lose the lognormal appearance of the distribution due to the use of an excessive number of classes) and provides a reliable uncertainty value.
## Getting Started: A step-by-step tutorial
> **Important note:**
-> Please, **update as soon as possible to version 1.4.2**. It is also advisable to **update the plotting library matplotlib to version 2.x** since the plots are optimized for such version.
+> Please, **update to version 1.4.4**. It is also advisable to **update the plotting library matplotlib to version 2.x** since all the plots are optimized for such version.
### *Open and running the script*
@@ -106,7 +130,7 @@ To use the script it is necessary to run it. To do this, just click on the green
The following text will appear in the shell/console (Fig. 1):
```
======================================================================================
-Welcome to GrainSizeTools script v1.4.2
+Welcome to GrainSizeTools script v1.4.4
======================================================================================
GrainSizeTools is a free open-source cross-platform script to visualize and characterize
@@ -114,9 +138,8 @@ the grain size in polycrystalline materials from thin sections and estimate diff
stresses via paleopizometers.
METHODS AVAILABLE
------------------
================== ==================================================================
-Function Description
+Functions Description
================== ==================================================================
extract_areas Extract the areas of the grains from a text file (txt, csv or xlsx)
calc_diameters Calculate the diameter via the equivalent circular diameter
@@ -125,11 +148,12 @@ derive3D Estimate the actual grain size distribution via steorology m
quartz_piezometer Estimate diff. stress from grain size in quartz using piezometers
olivine_piezometer Estimate diff. stress from grain size in olivine using piezometers
other_pizometers Estimate diff. stress from grain size in other phases
+confidence_interval Estimate the confidence interval using the t distribution
================== ==================================================================
You can get information on the different methods by:
- (1) Typing help(name of the method) in the console. e.g. >>> help(derive3D)
- (2) In the Spyder IDE by writing the name of the method and clicking Ctrl + I
+ (1) Typing help(function name) in the console. e.g. help(conf_interval)
+ (2) In the Spyder IDE by writing the name of the function and clicking Ctrl + I
(3) Visit script documentation at https://marcoalopez.github.io/GrainSizeTools/
@@ -190,7 +214,7 @@ To sum up, the name following the Python keyword ```def```, in this example ```c
The names of the Python functions in the script are self-explanatory and each one has been implemented to perform a single task. Although there are a lot of functions within the script, we will only need to call less than four functions to obtain the results.
-### *Using the script to visualize and estimate the grain size features*
+### *Using the script to visualize and estimate the grain size*
#### Loading the data and extracting the areas of the grain profiles
@@ -297,6 +321,7 @@ First note that contrary to what was shown so far, the function is called direct
NUMBER WEIGHTED APPROACH (linear apparent grain size):
Mean grain size = 35.79 microns
+Standard deviation = xx (1-sigma)
Median grain size = 32.53 microns
Interquartile range (IQR) = 23.98
@@ -317,7 +342,7 @@ Although we promote the use of frequency *vs* apparent grain size linear plot (F
```python
>>> find_grain_size(areas, diameters, plot='area')
```
-in this example setting to use the area-weighted plot. The name of the different plots available are ```'lin'``` for the linear number-weighted plot (the default), ```'area'``` for the area-weighted plot (as in the example above), ```'sqrt'``` for the square-root grain size plot, and ```'log'``` for the logarithmic grain size plot. Note that the selection of different type of plot also implies to obtain different grain size estimations.
+in this example setting to use the area-weighted plot. The name of the different plots available are ```'lin'``` for the linear number-weighted plot (the default), ```'area'``` for the area-weighted plot (as in the example above), ```'sqrt'``` for the square-root grain size plot, and ```'log'``` for the logarithmic grain size plot. Note that the selection of different scales also implies to obtain different grain size estimations. Last, it is very important to note that **the mean of the square root or logarithmic grain sizes is not the same as the square root or the logarithm of the grain size mean**!
The function includes different plug-in methods to estimate an "optimal" bin size, including an automatic mode. The default automatic mode ```'auto'``` use the Freedman-Diaconis rule when using large datasets (> 1000) and the Sturges rule for small datasets. Other available rules are the Freedman-Diaconis ```'fd'```, Scott ```'scott'```, Rice ```'rice'```, Sturges ```'sturges'```, Doane ```'doane'```, and square-root ```'sqrt'``` bin sizes. For more details on the methods see [here](https://docs.scipy.org/doc/numpy/reference/generated/numpy.histogram.html). We encourage you to use the default method ```'auto'```. Empirical experience indicates that the ```'doane'``` and ```'scott'``` methods work also pretty well when you have a lognormal- or a normal-like distributions, respectively. To specify the method we write in the shell:
@@ -333,12 +358,12 @@ note that you have to define first the type of plot you want and that the type o
The user-defined bin size can be any number of type integer or float (*i.e.* an irrational number).
-
-*Figure 6. Different apparent grain size vs frequency plots of the same population returned by the find_grain_size function. These include the number- (linear) and area-weighted plots (upper part) and the logarithmic and square root apparent grain sizes (lower part)*
+
+*Figure 6. Different apparent grain size vs frequency plots of the same population returned by the find_grain_size function. These include the number-weighted grain size distribution using linear (upper left), square root (upper right), or logarithmic (lower left) scales, and area-weighted distributions (lower right)*
#### *Estimating differential stress using piezometric relations (paleopiezometry)*
-The script includes several functions for estimating differential stress from apparent grain size (i.e. using piezometric relations). This includes mineral phases such as quartz, calcite, olivine and albite (other phases will be added in the future). The function requires measuring the grain size as equivalent circular diameters and entering the apparent grain sizes ***in microns***. There are three different functions for this: ```quartz_piezometer``` for quartz piezometers, ```olivine_piezometer``` for olivine piezometers, and ```other_piezometers``` for other mineral phases. We provide some examples below:
+The script includes several functions for estimating differential stress from apparent grain size (i.e. using piezometric relations). This includes mineral phases such as quartz, calcite, olivine and albite (other phases will be added in the future). The function requires measuring the grain size as equivalent circular diameters and entering the apparent grain sizes ***in microns***. There are three different functions for this: ```quartz_piezometer``` for quartz, ```olivine_piezometer``` for olivine, and ```other_piezometers``` for other mineral phases. We provide some examples below:
```python
>>> quartz_piezometer(grain_size=5.7, piezometer='Stipp_Tullis')
@@ -356,26 +381,28 @@ Ensure that you have entered the apparent grain size as the square root mean!
differential stress = 175.72 MPa
```
-It is key to note that different piezometers require entering **different types of apparent grain sizes** to provide meaningful estimates of differential stress. For example, the piezometer relation of Stipp and Tullis (2003) requires entering the grain size as *the square root mean grain size from equivalent circular diameters with no stereological correction* (i.e. mean sqrt apparent grain size), and so on. Table 1 show all the implemented piezometers in GrainSizeTools v1.4.2 and the apparent grain size required for each one. Despite some piezometers were originally calibrated using linear intercepts (LI), the script will always require entering a specific apparent grain size measured as equivalent circular diameters (ECD) since the script will automatically convert this ECD value to linear intercepts using the De Hoff and Rhines (1968) empirical relation.
+It is key to note that different piezometers require entering **different types of apparent grain sizes** to provide meaningful estimates of differential stress. For example, the piezometer relation of Stipp and Tullis (2003) requires entering the grain size as *the square root mean grain size from equivalent circular diameters with no stereological correction* (i.e. mean sqrt apparent grain size), and so on. Table 1 show all the implemented piezometers in GrainSizeTools v1.4.2 and the apparent grain size required for each one. Despite some piezometers were originally calibrated using linear intercepts (LI), the script will always require entering a specific apparent grain size measured as equivalent circular diameters (ECD), the script will automatically convert this ECD value to linear intercepts using the De Hoff and Rhines (1968) empirical relation.
**Table 1.** Relation of piezometers put in the GrainSizeTools script and the apparent grain size required to obtain meaningful differential stress estimates
-| Piezometer | Apparent grain sizea | DRX mechanism | Phase | Reference |
-| :----------------------------------: | :-----------------------------: | :------------: | :----------: | :---------------------------: |
-| ```'Stipp_Tullis'``` | Square root mean | Regimes 2, 3 | Quartz | Stipp & Tullis (2003) |
-| ```'Stipp_Tullis_BLG'``` | Square root mean | Regime 1 (BLG) | Quartz | Stipp & Tullis (2003) |
-| ```'Holyoke'``` | Square root mean | Regimes 2, 3 | Quartz | Holyoke and Kronenberg (2010) |
-| ```'Holyoke_BLG'``` | Square root mean | Regime 1 (BLG) | Quartz | Holyoke and Kronenberg (2010) |
-| ```'Shimizu'```b | Logarithmic median | SGR + GBM | Quartz | Shimizu (2008) |
-| ```'Cross'``` and ```'Cross_hr'``` | Square root mean | BLG, SGR | Quartz | Cross et al. (2017) |
-| ```'Twiss'```c | Logarithmic mean | Regimes 2, 3 | Quartz | Twiss (1977) |
-| ```'calcite_Rutter_SGR'``` | Square root mean | SGR | Calcite | Rutter (1995) |
-| ```'calcite_Rutter_GBM'``` | Square root mean | GBM | Calcite | Rutter (1995) |
-| ```'albite_PostT_BLG'```c | Median (linear scale) | BLG | Albite | Post and Tullis (1999) |
-| ```'VanderWal_wet'```c | Mean (linear scale) | | Olivine, wet | Van der Wal et al. (1993) |
-| ```'Jung_Karato'```c | Mean (linear scale) | BLG | Olivine, wet | Jung & Karato (2001) |
-*a) Apparent grain size measured as equivalent circular diameters (ECD) with no stereological correction and reported in microns either in linear, square root or logarithmic scales*
-*b) Shimizu piezometer requires to provide the temperature during deformation in K, the script will ask you to provide such value*
-*( c) These piezometers were originally calibrated using linear intercepts (LI) instead of ECD*
+
+| Piezometer | Apparent grain size† | DRX mechanism | Phase | Reference |
+| :--------------------------------: | :-------------------: | :------------: | :----------: | :---------------------------: |
+| ```'Stipp_Tullis'``` | Square root mean | Regimes 2, 3 | Quartz | Stipp & Tullis (2003) |
+| ```'Stipp_Tullis_BLG'``` | Square root mean | Regime 1 (BLG) | Quartz | Stipp & Tullis (2003) |
+| ```'Holyoke'``` | Square root mean | Regimes 2, 3 | Quartz | Holyoke and Kronenberg (2010) |
+| ```'Holyoke_BLG'``` | Square root mean | Regime 1 (BLG) | Quartz | Holyoke and Kronenberg (2010) |
+| ```'Shimizu'```*‡* | Logarithmic median | SGR + GBM | Quartz | Shimizu (2008) |
+| ```'Cross'``` and ```'Cross_hr'``` | Square root mean | BLG, SGR | Quartz | Cross et al. (2017) |
+| ```'Twiss'```*§* | Logarithmic mean | Regimes 2, 3 | Quartz | Twiss (1977) |
+| ```'calcite_Rutter_SGR'``` | Square root mean | SGR | Calcite | Rutter (1995) |
+| ```'calcite_Rutter_GBM'``` | Square root mean | GBM | Calcite | Rutter (1995) |
+| ```'albite_PostT_BLG'```*§* | Median (linear scale) | BLG | Albite | Post and Tullis (1999) |
+| ```'VanderWal_wet'```*§* | Mean (linear scale) | | Olivine, wet | Van der Wal et al. (1993) |
+| ```'Jung_Karato'```*§* | Mean (linear scale) | BLG | Olivine, wet | Jung & Karato (2001) |
+
+*† Apparent grain size measured as equivalent circular diameters (ECD) with no stereological correction and reported in microns either in linear, square root or logarithmic scales*
+*‡ Shimizu piezometer requires to provide the temperature during deformation in K*
+*§ These piezometers were originally calibrated using linear intercepts (LI) instead of ECD*
For more details on the piezometers and the assumption made use the command ```help()``` in the console as follows:
@@ -387,28 +414,48 @@ The constant values as put in the script are described in Table 2 below.
**Table 2**. Parameters relating the apparent size of dynamically recrystallized grains and the differential stress using a relation in the form ***d = Aσ-p*** or ***σ = Bd-m***
-| Reference | phase | DRX | Aa, b | pa | Ba, b | ma |
-| :-------------------------------------: | :----------: | :----------: | :--------------: | :-----------: | :--------------: | :-----------: |
-| Stipp and Tullis (2003) | quartz | Regimes 2, 3 | 3630.8 | 1.26 | 669.0 | 0.79 |
-| Stipp and Tullis (2003) | quartz | Regime 1 | 78 | 0.61 | 1264.1 | 1.64 |
-| Holyoke & Kronenberg (2010)c | quartz | Regimes 2, 3 | 2451 | 1.26 | 490.3 | 0.79 |
-| Holyoke & Kronenberg (2010)d | quartz | Regime 1 | 39 | 0.54 | 883.9 | 1.85 |
-| Shimizu (2008) | quartz | SGR + GBM | 1525 | 1.25 | 352 | 0.8 |
-| Cross et al. (2017)d | quartz | Regimes 2, 3 | 8128.3 | 1.41 | 593.0 | 0.71 |
-| Cross et al. (2017)d | quartz, hr | Regimes 2, 3 | 16595.9 | 1.59 | 450.9 | 0.63 |
-| Twiss (1977) | quartz | Regimes 2, 3 | 12.3 | 1.47 | 5.5 | 0.68 |
-| Jung and Karato (2001) | olivine, wet | BLG | 25704 | 1.18 | 5461.03 | 0.85 |
-| Van der Wal et al. (1993) | olivine, wet | | 0.0148 | 1.33 | 0.0425 | 0.75 |
-| Rutter (1995) | calcite | SGR | 2026.8 | 1.14 | 812.83 | 0.88 |
-| Rutter (1995) | calcite | GBM | 7143.8 | 1.12 | 2691.53 | 0.89 |
-| Post and Tullis (1999) | albite | BLG | 55 | 0.66 | 433.4 | 1.52 |
-*(a) ***B*** and ***m*** relate to ***A*** and ***p*** as follows: ***B = A1/p*** and ***m = 1/p****
-*(b) ***A*** and ***B*** are in [μm MPap, m] excepting Twiss (1977) [mm MPap, m] and Van der Wal et al. (1993) [m MPap, m]*
-*( c) Holyoke and Kronenberg (2010) is a linear recalibration of the Stipp and Tullis (2003) piezometer*
-*(d) Cross et al. (2017) reanalysed the samples of Stipp and Tullis (2003) using EBSD for grain reconstruction. Specifically, they use grain maps with a 1 μm step size and a 200 nm step size (hr - high resolution). This is the preferred piezometer for quartz when grain size data comes from EBSD*
-
-
-#### *Derive the actual 3D distribution of grain sizes from thin sections*
+| Reference | phase | DRX | A†,‡ | p† | B†,‡ | m† |
+| :----------------------------: | :----------: | :----------: | :-----: | :--: | :-----: | :--: |
+| Stipp and Tullis (2003) | quartz | Regimes 2, 3 | 3630.8 | 1.26 | 669.0 | 0.79 |
+| Stipp and Tullis (2003) | quartz | Regime 1 | 78 | 0.61 | 1264.1 | 1.64 |
+| Holyoke & Kronenberg (2010)*§* | quartz | Regimes 2, 3 | 2451 | 1.26 | 490.3 | 0.79 |
+| Holyoke & Kronenberg (2010)*§* | quartz | Regime 1 | 39 | 0.54 | 883.9 | 1.85 |
+| Shimizu (2008) | quartz | SGR + GBM | 1525 | 1.25 | 352 | 0.8 |
+| Cross et al. (2017)¶ | quartz | Regimes 2, 3 | 8128.3 | 1.41 | 593.0 | 0.71 |
+| Cross et al. (2017)¶ | quartz, hr | Regimes 2, 3 | 16595.9 | 1.59 | 450.9 | 0.63 |
+| Twiss (1977) | quartz | Regimes 2, 3 | 12.3 | 1.47 | 5.5 | 0.68 |
+| Jung and Karato (2001) | olivine, wet | BLG | 25704 | 1.18 | 5461.03 | 0.85 |
+| Van der Wal et al. (1993) | olivine, wet | | 0.0148 | 1.33 | 0.0425 | 0.75 |
+| Rutter (1995) | calcite | SGR | 2026.8 | 1.14 | 812.83 | 0.88 |
+| Rutter (1995) | calcite | GBM | 7143.8 | 1.12 | 2691.53 | 0.89 |
+| Post and Tullis (1999) | albite | BLG | 55 | 0.66 | 433.4 | 1.52 |
+
+*† **B** and **m** relate to **A** and **p** as follows: B = A1/p and m = 1/p*
+*‡ **A** and **B** are in [μm MPap, m] excepting Twiss (1977) in [mm MPap, m] and Van der Wal et al. (1993) in [m MPap, m]*
+*§ Holyoke and Kronenberg (2010) is a linear recalibration of the Stipp and Tullis (2003) piezometer*
+*¶ Cross et al. (2017) reanalysed the samples of Stipp and Tullis (2003) using EBSD data for reconstructing the grains. Specifically, they use grain maps with a 1 μm and a 200 nm (hr - high resolution) step sizes . This is the preferred piezometer for quartz when grain size data comes from EBSD maps*
+
+#### Estimating a robust confidence interval
+
+As pointed out in the scope section, the optimal approach is to obtain several measures of stress or grain sizes and then estimate a confidence interval. Since v1.4.4+, the script implements a function called ```confidende_interval```for this. The script assume that the sample size is small (< 10) and hence it uses the student's t-distribution with n-1 degrees of freedom to estimate a robust confidence interval. For large datasets the t-distribution approaches the normal distribution so you can also use this method for large datasets. The function has two inputs, the dataset, required, and the confidence interval, optional and set at 0.95 by default. For example:
+
+```python
+>>> my_results = [165.3, 174.2, 180.1]
+>>> confidence_interval(data=my_results, confidence=0.95)
+```
+
+The function will return the following information in the console:
+
+```
+Confidence set at 95.0 %
+Mean = 173.2 ± 18.51
+Max / min = 191.71 / 154.69
+Coefficient of variation = 10.7 %
+```
+
+The coefficient of variation express the confidence interval in percentage respect to the mean and thus it can be used to compare confidence intervals between samples with different mean values.
+
+#### Derive the actual 3D distribution of grain sizes from thin sections
The function responsible to unfold the distribution of apparent grain sizes into the actual 3D grain size distribution is named ```derive3D```. The script implements two methods to do this, the Saltykov and the two-step methods. The Saltykov method is the best option for exploring the dataset and for estimating the volume of a particular grain size fraction. The two-step method is suitable to describe quantitatively the shape of the grain size distribution assuming that they follow a lognormal distribution. This means that the two-step method only yield consistent results when the population of grains considered are completely recrystallized or when the non-recrystallized grains can be previously discarded using shape descriptors or any other relevant paramater such as the density of dislocations. It is therefore necessary to check first whether the linear distribution of grain sizes is unimodal and lognormal-like (i.e. skewed to the right as in the example shown in figure 7). For more details see [Lopez-Sanchez and Llana-Fúnez (2016)](http://www.sciencedirect.com/science/article/pii/S0191814116301778).
@@ -500,17 +547,20 @@ Then we create the plot (Fig. 10):
To create a more convenience plot (Fig. 10) we propose using the following **optional** parameters:
```python
-# First make a list specifying the labels of the samples (this is optional)
+# First make a list specifying the labels of the samples (this is optional). Ensure that the number of items in the brackets coincide with the number of datasets to plot.
>>> label_list = ['SampleA', 'SampleB', 'SampleC', 'SampleD']
# Then make the plot ading the following instructions
>>> plt.boxplot(all_data, vert=False, meanline=True, showmeans=True, labels=label_list)
-# vert -> if False makes the boxes horizontal instead of vertical
-# meanline and showmeans -> if True will show the location of the mean within the plots
-# labels -> add labels to the different datasets. Ensure that the number of items in the brackets coincide with the number of datasets to plot.
>>> plt.xlabel('apparent diameter ($\mu m$)') # add the x-axis label
>>> plt.show() # write this and click return if the plot did not appear automatically
```
+The parameters defined in the boxplot are:
+
+- ```vert```: if False makes the boxes horizontal instead of vertical (it is True by default).
+- ```meanline``` and ```showmeans```: if True will show the location of the mean within the plots.
+- ```labels```: add labels to the different datasets.
+
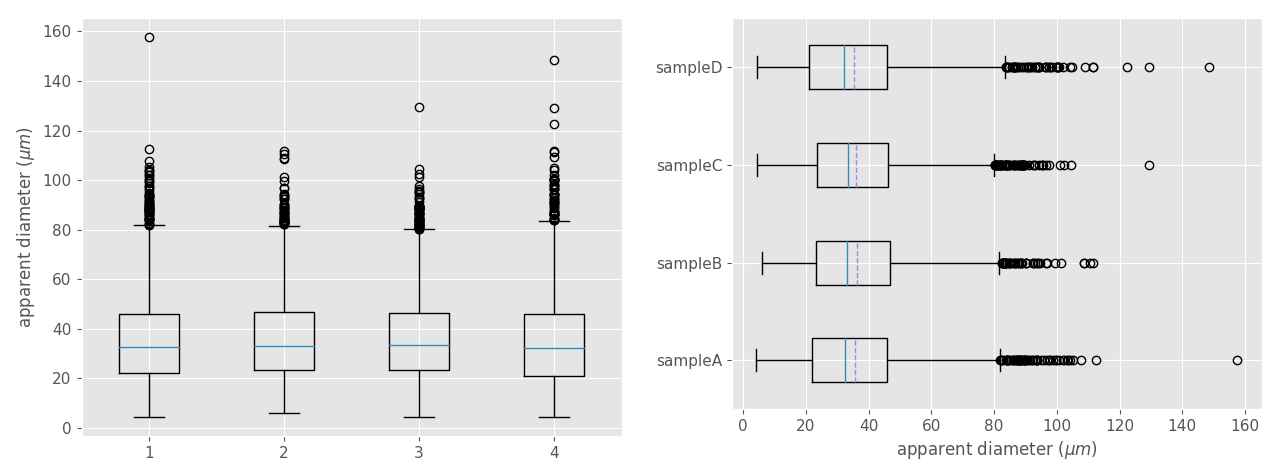
*Figure 10. Box plot comparing four unimodal datasets obtained from the same sample but located in different places along the thin section. At left, a box plot with the default appearance. At right, the same box plot with the optional parameters showing above. Dashed lines are the mean. Note that the all the datasets show similar median, means, IQRs, and whisker locations. In contrast, the fliers (points) approximately above 100 microns vary greatly.*
@@ -656,24 +706,27 @@ derive3D(diameters, numbins=12, set_limit=None, fit=True, initial_guess=True)
## How to measure the areas of the grain profiles with ImageJ
-**Before you start:** This tutorial assumes that you have installed the ImageJ application. If this is not the case, go [here](http://imagej.nih.gov/ij/) to download and install it. You can also install different flavours of the ImageJ application that will work in a similar way (see [here](http://fiji.sc/ImageJ) for a summary) . As a cautionary note, this is not a detailed tutorial on image analysis using ImageJ at all, but a quick systematic tutorial on how to measure the areas of the grain profiles from a thin section to later estimate the grain size and grain size distribution using the GrainSizeTools script. If you are interested in image analysis methods (e.g. grain segmentation techniques, shape characterization, etc.) you should have a look at the list of references at the end of this tutorial.
+> **Before you start:** This tutorial assumes that you have installed the ImageJ application. If this is not the case, go [here](http://imagej.nih.gov/ij/) to download and install it. You can also install different flavours of the ImageJ application that will work in a similar way (see [here](http://fiji.sc/ImageJ) for a summary) . As a cautionary note, this is not a detailed tutorial on image analysis methods using ImageJ, but a quick systematic tutorial on how to measure the areas of the grain profiles from a thin section to later estimate the grain size and grain size distribution using the GrainSizeTools script. If you are interested in image analysis methods (e.g. grain segmentation techniques, shape characterization, etc.) you should have a look at the list of references at the end of this tutorial.
### *Previous considerations on the Grain Boundary Maps*
-Grain size studies in rocks are usually based on measures performed in thin sections (2D data) through image analysis. Since the methods implemented in the GrainSizeTools script are based on the measure of the areas of the grain profiles, the first step is therefore to obtain a grain boundary map from the thin section (Fig. 11).
+Grain size studies in rocks are usually based on measures performed in thin sections (2D data) through image analysis. Since the methods implemented in the GrainSizeTools script are based on the measure of the areas of the grain profiles, the first step is therefore to obtain a grain boundary map from the thin section (Fig. 1).
+
+
+*Figure 1. An example of a grain boundary map*
-
-*Figure 11. An example of a grain boundary map*
+Nowadays, these measures are mostly made on digital images made by pixels (e.g. Heilbronner and Barret 2014), also known as raster graphics image. You can obtain some information on raster graphics [here](https://en.wikipedia.org/wiki/Raster_graphics). For example, in a 8-bit grayscale image -the most used type of grayscale image-, each pixel contains three values: information about its location in the image -their x and y coordinates- and its 'grey' value in a range that goes from 0 (white) to 256 (black) (i.e. it allows 256 different grey intensities). In the case of a grain boundary map (Fig. 1), we usually use a binary image where only two possible values exist, 0 for white pixels and 1 for black pixels.
-Nowadays, these measures are mostly made on digital images made by pixels (e.g. Heilbronner and Barret 2014), also known as raster graphics image. You can obtain some information on raster graphics [here](https://en.wikipedia.org/wiki/Raster_graphics). For example, in a 8-bit grayscale image -the most used type of grayscale image-, each pixel contains three values: information about its location in the image -their x and y coordinates- and its 'gray' value in a range that goes from 0 (white) to 256 (black) (i.e. it allows 256 different gray intensities). In the case of a grain boundary map (Fig. 11), we usually use a binary image where only two possible values exist, 0 for white pixels and 1 for black pixels.
+One of the key points about raster images is that they are resolution dependent, which means that each pixel have a physical dimension. Consequently, the smaller the size of the pixel, the higher the resolution. The resolution depends on the number of pixels per unit area or length, and it is usually measured in pixel per (square) inch (PPI) (more information about [Image resolution](https://en.wikipedia.org/wiki/Image_resolution) and [Pixel density](https://en.wikipedia.org/wiki/Pixel_density)). This concept is key since the resolution of our raw image -the image obtained directly from the microscope- will limit the precision of the measures. Known the size of the pixels is therefore essential and it will allow us to set the scale of the image to measure of the areas of the grain profiles. In addition, it will allow us to later make a perimeter correction when calculating the equivalent diameters from the areas of the grain profiles. So be sure about the image resolution at every step, from the "raw" image you get from the microscope until you get the grain boundary map.
-One of the key points on raster images is that they are resolution dependent, which means that each pixel have a physical dimension. Consequently, the smaller the size of the pixel, the higher the resolution. The resolution depends on the number of pixels per unit area or length, and it is usually measured in pixel per (square) inch (PPI) (more information about [Image resolution](https://en.wikipedia.org/wiki/Image_resolution) and [Pixel density](https://en.wikipedia.org/wiki/Pixel_density)). This concept is key since the resolution of our raw image -the image obtained directly from the microscope- will limit the precision of the measures. Known the size of the pixels is therefore essential and it will allow us to set the scale of the image to measure of the areas of the grain profiles. In addition, it will allow us to later make a perimeter correction when calculating the equivalent diameters from the areas of the grain profiles. So be sure about the image resolution at every step, from the raw image until you get the grain boundary map.
+> Note: It is important not to confuse the pixel resolution with the actual spatial resolution of the image. The spatial resolution is the actual resolution of the image and it is limited physically not by the number of pixels per unit area/length. For example, conventional SEM techniques have a maximum spatial resolution of 50 to 100 nm whatever the pixels in the image recorded. Think in a digital image of a square inch in size and made of just one black pixel (i.e. with a resolution of ppi = 1). If we double the resolution of the image, we will obtain the same image but now formed by four black pixels instead of one. The new pixel resolution per unit length will be ppi = 2 (or 4 per unit area), however, the spatial resolution of the image remains the same. Strictly speaking, the spatial resolution refers to the number of independent pixel values per unit area/length.
-> Note: It is important not to confuse the pixel resolution with the actual spatial resolution of the image. The spatial resolution is the actual resolution of the image and it is limited physically not by the number of pixels per unit area/length. For example, conventional SEM techniques have a maximum spatial resolution of 50 to 100 nm whatever the pixels in the image recorded. Think in a digital image of a square inch in size and made of just one black pixel (i.e. with a resolution of ppi = 1). If we double the resolution of the image, we will obtain the same image but now formed by four black pixels instead of one. The new pixel resolution per unit length will be ppi = 2 (or ppi = 4 per unit area). In contrast, the spatial resolution of the image remains the same. Strictly speaking, the spatial resolution refers to the number of independent pixel values per unit area/length.
+The techniques that make possible the transition from a raw image to a grain boundary map, known as grain segmentation, are numerous and depend largely on the type of image obtained from the microscope. Thus, digital images may come from transmission or reflected light microscopy, semi-automatic techniques coupled to light microscopy such as the CIP method (e.g. Heilbronner 2000), electron microscopy either from BSD images or EBSD grain maps, or even from electron microprobes through compositional mapping. All this techniques produce very different images (i.e. different resolutions, colour *vs* grey scale, nature of the artefacts, grain size boundary *vs* phase maps, etc.). The presentation of this segmentation techniques is beyond the scope of this tutorial and the reader is referred to the references cited at the end of this document and, particularly, to the books written by Russ (2011) and Heilbronner and Barret (2014). This tutorial is focused instead on the features of the grain boundary maps by itself not in how to convert the raw images to grain boundary maps using manual, automatic or semi-automatic grain segmentation.
-The techniques that make possible the transition from a raw image to a grain boundary map, known as grain segmentation, are numerous and depend largely on the type of image obtained from the microscope. Thus, digital images may come from transmission or reflected light microscopy, semi-automatic techniques coupled to light microscopy such as the CIP method (e.g. Heilbronner 2000), electron microscopy either from BSD images or EBSD grain maps, or even from electron microprobes through compositional mapping. All this techniques produce very different images (i.e. different resolutions, color *vs* gray scale, nature of the artefacts, grain size boundary *vs* phase maps, etc.). The presentation of this image analysis techniques is beyond the scope of this tutorial and the reader is referred to the references cited at the end of this document and, particularly, to the books written by Russ (2011) and Heilbronner and Barret (2014). Hence, this tutorial is focused on the features of the grain boundary maps by itself not in how to convert the raw images to grain boundary maps using manual, automatic or semi-automatic grain segmentation.
+Once the grain segmentation is done, it is crucial to ensure that at the actual pixel resolution the grain boundaries have a width of two or three pixels (Fig. 2). This will prevent the formation of undesirable artefacts since when two black pixels belonging to two different grains are adjacent to each other, both grains will be considered the same grain by the image analysis software.
-Once the grain segmentation is done, it is crucial to ensure that at the actual pixel resolution the grain boundaries have a width of two or more pixels (Fig. 5). This will prevent the formation of undesirable artefacts since when two black pixels belonging to two different grains are adjacent to each other, both grains will be considered the same grain by the image analysis software.
+ +*Figure 2. Detail of grain boundaries in a grain boundary map. The figure shows the boundaries (in white) between three grains in a grain boundary map. The squares represent the pixels in the image. The boundaries are two pixels wide approximately.*
### *Measuring the areas of the grain profiles*
@@ -681,25 +734,25 @@ Once the grain segmentation is done, it is crucial to ensure that at the actual
2) To measure the areas of the grain profiles it is first necessary to convert the grain boundary map into a binary image. If this was not done previously, go to ```Process>Binary``` and click on ```Make binary```. Also, make sure that the areas of grain profiles are in black and the grain boundaries in white and not the other way around. If not, invert the image in ```Edit>Invert```.
-3) Then, it is necessary to set the scale of the image. Go to ```Analize>Set Scale```. A new window will appear (Fig. 12). To set the scale, you need to know the size of a feature, such as the width of the image, or the size of an object such as a scale bar. The size of the image in pixels can be check in the upper left corner of the window, within the parentheses, containing the image. To use a particular object of the image as scale the procedure is: i) Use the line selection tool in the tool bar (Fig. 12) and draw a line along the length of the feature or scale bar; ii) go to ```Analize>Set Scale```; iii) the distance of the drawn line in pixels will appear in the upper box, so enter the dimension of the object/scale bar in the 'known distance' box and set the units in the 'Unit length' box; iv) do not check 'Global' unless you want that all your images have the same calibration and click ok. Now, you can check in the upper left corner of the window the size of the image in microns (millimetres or whatever) and in pixels.
+3) Then, it is necessary to set the scale of the image. Go to ```Analize>Set Scale```. A new window will appear (Fig. 3). To set the scale, you need to know the size of a feature, such as the width of the image, or the size of an object such as a scale bar. The size of the image in pixels can be check in the upper left corner of the window, within the parentheses, containing the image. To use a particular object of the image as scale the procedure is: i) Use the line selection tool in the tool bar (Fig. 3) and draw a line along the length of the feature or scale bar; ii) go to ```Analize>Set Scale```; iii) the distance of the drawn line in pixels will appear in the upper box, so enter the dimension of the object/scale bar in the 'known distance' box and set the units in the 'Unit length' box; iv) do not check 'Global' unless you want that all your images have the same calibration and click ok. Now, you can check in the upper left corner of the window the size of the image in microns (millimetres or whatever) and in pixels.
-
-*Figure 12. At left, the Set Scale window. In the upper right, the ImageJ menu and tool bars. The line selection tool is the fifth element from the left (which is actually selected). In the bottom right, the upper left corner of the window that contains the grain boundary map. The numbers are the size in microns and the size in pixels (in brackets).*
+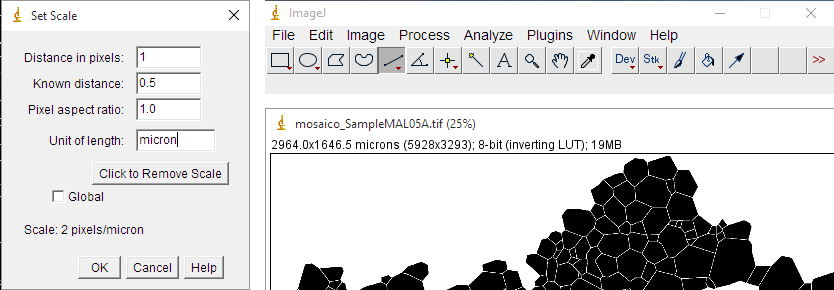
+*Figure 3. At left, the Set Scale window. In the upper right, the ImageJ menu and tool bars. The line selection tool is the fifth element from the left (which is actually selected). In the bottom right, the upper left corner of the window that contains the grain boundary map. The numbers are the size in microns and the size in pixels (in brackets).*
4) The next step requires to set the measurements to be done. For this, go to ```Analize>Set Measurements``` and a new window will appear. Make sure that 'Area' is selected. You can also set at the bottom of the window the desired number of decimal places. Click ok.
-5) To measure the areas of our grain profiles we need to go to ```Analize>Analize Particles```. A new window will appear with different options (Fig. 13). The first two are for establishing certain conditions to exclude anything that is not an object of interest in the image. The first one is based on the size of the objects in pixels by establishing a range of size. We usually set a minimum of four pixels and the maximum set to infinity to rule out possible artefacts hard to detect by the eye. This ultimately depends on the quality and the nature of your grain boundary map. For example, people working with high-resolution EBSD maps usually discard any grain with less than ten pixels. The second option is based on the roundness of the grains. We usually leave the default range values 0.00-1.00, but again this depends on your data and purpose. For example, the roundness parameter could be useful to differentiate between non-recrystallized and recrystallized grains in some cases. Just below, the 'show' drop-down menu allows the user to obtain different types of images when the particle analysis is done. We usually set this to 'Outlines' to obtain an image with all the grains measured outlined and numbered, which can be useful later to check the data set. Finally, the user can choose between different options. In our case, it is just necessary to select 'Display results'. Click ok.
+5) To measure the areas of our grain profiles we need to go to ```Analize>Analize Particles```. A new window will appear with different options (Fig. 4). The first two are for establishing certain conditions to exclude anything that is not an object of interest in the image. The first one is based on the size of the objects in pixels by establishing a range of size. We usually set a minimum of four pixels and the maximum set to infinity to rule out possible artefacts hard to detect by the eye. This ultimately depends on the quality and the nature of your grain boundary map. For example, people working with high-resolution EBSD maps usually discard any grain with less than ten pixels. The second option is based on the roundness of the grains. We usually leave the default range values 0.00-1.00, but again this depends on your data and purpose. For example, the roundness parameter could be useful to differentiate between non-recrystallized and recrystallized grains in some cases. Just below, the 'show' drop-down menu allows the user to obtain different types of images when the particle analysis is done. We usually set this to 'Outlines' to obtain an image with all the grains measured outlined and numbered, which can be useful later to check the data set. Finally, the user can choose between different options. In our case, it is just necessary to select 'Display results'. Click ok.
-
-*Figure 13. Analyse particles window showing the different options*
+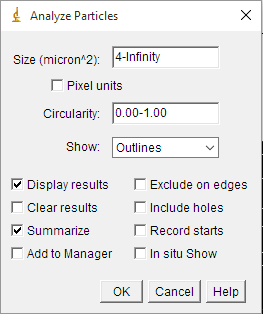
+*Figure 4. Analyze particles window showing the different options*
-6) After a while, several windows will appear. At least, one containing the results of the measures (Fig. 14), and other containing the image with the grains outlined and numbered. Note that the numbers displayed within the grains in the image correspond to the values showed in the first column of the results. To save the image go to the ImageJ menu bar, click on ```File>Save As```, and choose the file type you prefer (we encourage you to use PNG or TIFF for such type of image). To save the results we have different options. In the menu bar of the window containing the results, go to ```Results>Options``` and a new window will appear (Fig. 15). In the third line, you can choose to save the results as a text (.txt), csv comma-separated (.csv) or excel (.xls) file types. We encourage you to choose either *txt* or *csv* since both are widely supported formats to exchange tabular data. Regarding the 'Results Table Options' at the bottom, make sure that 'Save column headers' are selected since this headers will be used by the GrainSizeTools script to automatically extract the data from the column 'Area'. Finally, in the same window go to ```File>Save As``` and choose a name for the file. You are done.
+6) After a while, several windows will appear. At least, one containing the results of the measures (Fig. 5), and other containing the image with the grains outlined and numbered. Note that the numbers displayed within the grains in the image correspond to the values showed in the first column of the results. To save the image go to the ImageJ menu bar, click on ```File>Save As```, and choose the file type you prefer (we encourage you to use PNG or TIFF for such type of image). To save the results we have different options. In the menu bar of the window containing the results, go to ```Results>Options``` and a new window will appear (Fig. 6). In the third line, you can choose to save the results as a text (.txt), csv comma-separated (.csv) or excel (.xls) file types. We encourage you to choose either *txt* or *csv* since both are widely supported formats to exchange tabular data. Regarding the 'Results Table Options' at the bottom, make sure that 'Save column headers' are selected since this headers will be used by the GrainSizeTools script to automatically extract the data from the column 'Area'. Finally, in the same window go to ```File>Save As``` and choose a name for the file. You are done.
-
-*Figure 14. Window with the ImageJ output showing all the measures done on the grains.*
+
+*Figure 2. Detail of grain boundaries in a grain boundary map. The figure shows the boundaries (in white) between three grains in a grain boundary map. The squares represent the pixels in the image. The boundaries are two pixels wide approximately.*
### *Measuring the areas of the grain profiles*
@@ -681,25 +734,25 @@ Once the grain segmentation is done, it is crucial to ensure that at the actual
2) To measure the areas of the grain profiles it is first necessary to convert the grain boundary map into a binary image. If this was not done previously, go to ```Process>Binary``` and click on ```Make binary```. Also, make sure that the areas of grain profiles are in black and the grain boundaries in white and not the other way around. If not, invert the image in ```Edit>Invert```.
-3) Then, it is necessary to set the scale of the image. Go to ```Analize>Set Scale```. A new window will appear (Fig. 12). To set the scale, you need to know the size of a feature, such as the width of the image, or the size of an object such as a scale bar. The size of the image in pixels can be check in the upper left corner of the window, within the parentheses, containing the image. To use a particular object of the image as scale the procedure is: i) Use the line selection tool in the tool bar (Fig. 12) and draw a line along the length of the feature or scale bar; ii) go to ```Analize>Set Scale```; iii) the distance of the drawn line in pixels will appear in the upper box, so enter the dimension of the object/scale bar in the 'known distance' box and set the units in the 'Unit length' box; iv) do not check 'Global' unless you want that all your images have the same calibration and click ok. Now, you can check in the upper left corner of the window the size of the image in microns (millimetres or whatever) and in pixels.
+3) Then, it is necessary to set the scale of the image. Go to ```Analize>Set Scale```. A new window will appear (Fig. 3). To set the scale, you need to know the size of a feature, such as the width of the image, or the size of an object such as a scale bar. The size of the image in pixels can be check in the upper left corner of the window, within the parentheses, containing the image. To use a particular object of the image as scale the procedure is: i) Use the line selection tool in the tool bar (Fig. 3) and draw a line along the length of the feature or scale bar; ii) go to ```Analize>Set Scale```; iii) the distance of the drawn line in pixels will appear in the upper box, so enter the dimension of the object/scale bar in the 'known distance' box and set the units in the 'Unit length' box; iv) do not check 'Global' unless you want that all your images have the same calibration and click ok. Now, you can check in the upper left corner of the window the size of the image in microns (millimetres or whatever) and in pixels.
-
-*Figure 12. At left, the Set Scale window. In the upper right, the ImageJ menu and tool bars. The line selection tool is the fifth element from the left (which is actually selected). In the bottom right, the upper left corner of the window that contains the grain boundary map. The numbers are the size in microns and the size in pixels (in brackets).*
+
+*Figure 3. At left, the Set Scale window. In the upper right, the ImageJ menu and tool bars. The line selection tool is the fifth element from the left (which is actually selected). In the bottom right, the upper left corner of the window that contains the grain boundary map. The numbers are the size in microns and the size in pixels (in brackets).*
4) The next step requires to set the measurements to be done. For this, go to ```Analize>Set Measurements``` and a new window will appear. Make sure that 'Area' is selected. You can also set at the bottom of the window the desired number of decimal places. Click ok.
-5) To measure the areas of our grain profiles we need to go to ```Analize>Analize Particles```. A new window will appear with different options (Fig. 13). The first two are for establishing certain conditions to exclude anything that is not an object of interest in the image. The first one is based on the size of the objects in pixels by establishing a range of size. We usually set a minimum of four pixels and the maximum set to infinity to rule out possible artefacts hard to detect by the eye. This ultimately depends on the quality and the nature of your grain boundary map. For example, people working with high-resolution EBSD maps usually discard any grain with less than ten pixels. The second option is based on the roundness of the grains. We usually leave the default range values 0.00-1.00, but again this depends on your data and purpose. For example, the roundness parameter could be useful to differentiate between non-recrystallized and recrystallized grains in some cases. Just below, the 'show' drop-down menu allows the user to obtain different types of images when the particle analysis is done. We usually set this to 'Outlines' to obtain an image with all the grains measured outlined and numbered, which can be useful later to check the data set. Finally, the user can choose between different options. In our case, it is just necessary to select 'Display results'. Click ok.
+5) To measure the areas of our grain profiles we need to go to ```Analize>Analize Particles```. A new window will appear with different options (Fig. 4). The first two are for establishing certain conditions to exclude anything that is not an object of interest in the image. The first one is based on the size of the objects in pixels by establishing a range of size. We usually set a minimum of four pixels and the maximum set to infinity to rule out possible artefacts hard to detect by the eye. This ultimately depends on the quality and the nature of your grain boundary map. For example, people working with high-resolution EBSD maps usually discard any grain with less than ten pixels. The second option is based on the roundness of the grains. We usually leave the default range values 0.00-1.00, but again this depends on your data and purpose. For example, the roundness parameter could be useful to differentiate between non-recrystallized and recrystallized grains in some cases. Just below, the 'show' drop-down menu allows the user to obtain different types of images when the particle analysis is done. We usually set this to 'Outlines' to obtain an image with all the grains measured outlined and numbered, which can be useful later to check the data set. Finally, the user can choose between different options. In our case, it is just necessary to select 'Display results'. Click ok.
-
-*Figure 13. Analyse particles window showing the different options*
+
+*Figure 4. Analyze particles window showing the different options*
-6) After a while, several windows will appear. At least, one containing the results of the measures (Fig. 14), and other containing the image with the grains outlined and numbered. Note that the numbers displayed within the grains in the image correspond to the values showed in the first column of the results. To save the image go to the ImageJ menu bar, click on ```File>Save As```, and choose the file type you prefer (we encourage you to use PNG or TIFF for such type of image). To save the results we have different options. In the menu bar of the window containing the results, go to ```Results>Options``` and a new window will appear (Fig. 15). In the third line, you can choose to save the results as a text (.txt), csv comma-separated (.csv) or excel (.xls) file types. We encourage you to choose either *txt* or *csv* since both are widely supported formats to exchange tabular data. Regarding the 'Results Table Options' at the bottom, make sure that 'Save column headers' are selected since this headers will be used by the GrainSizeTools script to automatically extract the data from the column 'Area'. Finally, in the same window go to ```File>Save As``` and choose a name for the file. You are done.
+6) After a while, several windows will appear. At least, one containing the results of the measures (Fig. 5), and other containing the image with the grains outlined and numbered. Note that the numbers displayed within the grains in the image correspond to the values showed in the first column of the results. To save the image go to the ImageJ menu bar, click on ```File>Save As```, and choose the file type you prefer (we encourage you to use PNG or TIFF for such type of image). To save the results we have different options. In the menu bar of the window containing the results, go to ```Results>Options``` and a new window will appear (Fig. 6). In the third line, you can choose to save the results as a text (.txt), csv comma-separated (.csv) or excel (.xls) file types. We encourage you to choose either *txt* or *csv* since both are widely supported formats to exchange tabular data. Regarding the 'Results Table Options' at the bottom, make sure that 'Save column headers' are selected since this headers will be used by the GrainSizeTools script to automatically extract the data from the column 'Area'. Finally, in the same window go to ```File>Save As``` and choose a name for the file. You are done.
-
-*Figure 14. Window with the ImageJ output showing all the measures done on the grains.*
+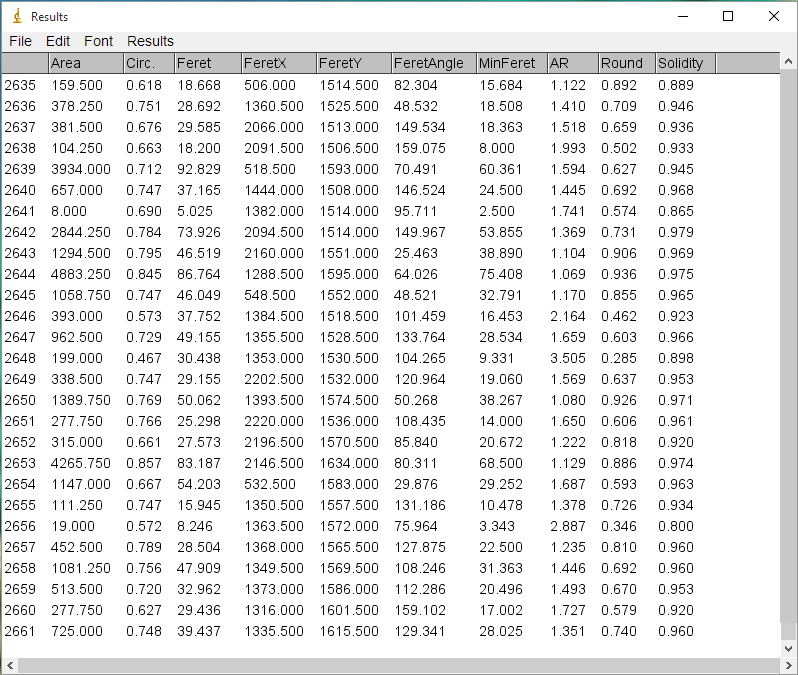 +*Figure 5. The results windows showing all the measures done on the grains by the ImageJ application.*
-
-*Figure 15. ImageJ I/O options window.*
+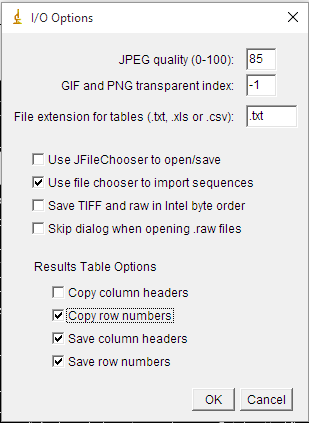
+*Figure 6. ImageJ I/O options window.*
@@ -728,12 +781,28 @@ Barraud, J., 2006. The use of watershed segmentation and GIS software for textur
## Frequently Asked Questions
***Who is this script for?***
-This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate features of the actual 3D distribution of grain sizes from the population of apparent grain sizes measured in thin sections. These features include the estimation of the volume occupied by a particular grain size fraction and the parameters that best describe the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods implemented in the script assume that the grains have equant or near-equant (AR < 2.0) shapes, which includes most dynamically recrystallized grains typically found in crustal and mantle shear zones (olivine, quartz, feldspar or calcite) and ice when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* (Higgins 2000). See the references list section for details.
+This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate the actual (3D) distribution of grain sizes from thin sections using stereological methods. The latter point includes an estimate of the volume occupied by a particular grain size fraction and a parameter to measure the shape of the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods assume that grains have equant or near-equant (AR < 2.0) shapes, which includes grains produced during static annealing and dynamically recrystallized grains when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For igneous studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* software (Higgins 2000). See the references list section for details.
+
+***Why use apparent grain size measures instead of measures estimated from unfolded 3D grain size distributions in paleopiezometry studies?***
+One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other unidimensional parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and, hence, the accuracy of the estimates depends not only in the introduction of errors during measuring but also on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, [only approximate](http://doi.wiley.com/10.1111/j.1365-2818.1983.tb04255.x). This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. To sum up, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distribution, otherwise use estimates based on the apparent grain size distribution.
+
+***What "average" (mean, median, peak) apparent grain size measure do I use?***
-***Why use apparent grain size measures instead of measures estimated from the unfolded 3D grain size distribution in paleopiezometry studies?***
-One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other 1D parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and hence the accuracy of the estimates depends on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, only approximate. This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. In short, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distributions, otherwise use measures based on the apparent grain size distribution.
+This depends on the features of the grain size distribution. In the case of unimodal distributions the following rule of thumb should be considered:
-***Why the grain size distribution plots produced by the GST script do not use the same units as the classic CSD charts?***
+- use **mean and standard deviation (SD)** when your **distribution is normal-like**
+- use **median and interquartile (or interprecentil) range** when your **distribution is skewed**
+
+If your distribution is multimodal (two or more frequency peaks), you can use for comparative purposes the **location of the frequency peaks** based on the Kernel density estimate. For more details read the [Scope](https://github.com/marcoalopez/GrainSizeTools/blob/master/DOCS/Scope.md) section.
+
+***What is an MSD value? What is it used for?***
+MSD stands for *Multiplicative Standard Deviation* and it is a parameter that allows to define the shape of the grain size distribution using a single value assuming that it follows a lognormal distribution. In plain language, the MSD value gives a measure of the asymmetry (or skewness) of the grain size distribution. For example, an MSD value equal to one corresponds to a normal (Gaussian) distribution and values greater than one with log-normal distributions of different shapes, being the higher the MSD value the greater the asymmetry of the distribution (Figure a). The advantage of this approach is that by using a single parameter we can define the shape of the grain size distribution independently of its scale (Fig. b), which is very convenient for comparing the shape of two or more grain size distributions.
+
+
+
+*Probability density functions of selected lognormal distributions taken from [Lopez-Sanchez and Llana-Fúnez (2016)](http://www.sciencedirect.com/science/article/pii/S0191814116301778). (a) Lognormal distributions with different MSD values (shapes) and the same median (4). (b) Lognormal distributions with the same shape corresponding to an MSD value (1.5) and different medians (note that different medians imply different scales in the horizontal and vertical directions).*
+
+***Why the grain size distribution plots produced by the GST script and the classic CSD charts do not use the same units on the y axis?***
As you may noticed classic CSDs charts (Marsh, 1988) show in the vertical axis the logarithmic variation in population density or log(frequency) in mm-4, while the stereological methods put in the GrainSizeTools (GST) script returns plots with a linear frequency (per unit volume). This is due to the different aims of the CSDs and the plots returned by the GST script. Originally, CSDs were built for deriving two things in magmatic systems: i) nucleation rates and ii) crystal growth rates. In these systems, small grains are more abundant than the large ones and the increase in quantity is typically exponential. The use of the logarithm in the vertical axis helps to obtain a straight line with the slope being the negative inverse of the crystal growth times the time of crystallization. Further, the intercept of the line at grain size equal to zero allows estimating the nuclei population density. In recrystallized rocks, there is no grain size equal to zero and we usually unknown the crystallization time, so the use of the CSDs are not optimal. Furthermore, the use of the logarithm in the vertical axis has two main disadvantages for microstructural studies: (i) it obscures the reading of the volume of a particular grain fraction, a common target in microtectonic studies, and (ii) it prevents the easy identification of the features of grain size distribution, which is relevant for applying the two-step method.
***Why the sum of all frequencies in the histograms is not equal to one?***
@@ -741,20 +810,26 @@ This is because the script normalized the frequencies of the different classes s
***Is it necessary to specify the version of the script used in a publication? How can this be indicated?***
-Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered a posteriori. The way to indicate the version is twofold:
+Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered later. The way to indicate the version is twofold:
+
+- The easy way we advise you to follow is by explicitly indicating the version in your manuscript as follows: "*...we used the GrainSizeTools script version 1.4.4...*" and then use the general citation in the reference list.
+
+- The other way is by adding a termination in the form *.v plus a number* in the general DOI link. This is, instead of using the general reference of the script:
+
+ Lopez-Sanchez, Marco A. (2018): GrainSizeTools script. figshare.
-- In the text by explicitly indicating it as follows: "*...we used the GrainSizeTools script version 1.4.1...*"
+ https://doi.org/10.6084/m9.figshare.1383130
-- In the reference list by adding a termination in the form *.v plus a number* in the general DOI link. For example:
+ You can modify the doi link as follows:
Lopez-Sanchez, Marco A. (2017): GrainSizeTools script. figshare.
https://doi.org/10.6084/m9.figshare.1383130.v15 (Note the termination *.v15*)
- To know what termination to use go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
+ To get the specific doi link, go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
***Does the script work with Python 2.7.x and 3.x versions? Which version do I choose?***
-Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons and they are widely used, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the author using Python 3.
+Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the maintainer using Python 3.
***I get the results but not the plots when using the Spyder IDE***
This issue is produced because the size of the figures returned by the script are too large to show them inside the console using the **inline** mode. To fix this go to the Spyder menu bar and in ```Tools>Preferences>IPython console>Graphics``` find *Graphics backend* and select *Automatic*.
diff --git a/DOCS/sourceDoc_to_pdf.pdf b/DOCS/sourceDoc_to_pdf.pdf
index c6e5e02..ccf4619 100644
Binary files a/DOCS/sourceDoc_to_pdf.pdf and b/DOCS/sourceDoc_to_pdf.pdf differ
+*Figure 5. The results windows showing all the measures done on the grains by the ImageJ application.*
-
-*Figure 15. ImageJ I/O options window.*
+
+*Figure 6. ImageJ I/O options window.*
@@ -728,12 +781,28 @@ Barraud, J., 2006. The use of watershed segmentation and GIS software for textur
## Frequently Asked Questions
***Who is this script for?***
-This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate features of the actual 3D distribution of grain sizes from the population of apparent grain sizes measured in thin sections. These features include the estimation of the volume occupied by a particular grain size fraction and the parameters that best describe the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods implemented in the script assume that the grains have equant or near-equant (AR < 2.0) shapes, which includes most dynamically recrystallized grains typically found in crustal and mantle shear zones (olivine, quartz, feldspar or calcite) and ice when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* (Higgins 2000). See the references list section for details.
+This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate the actual (3D) distribution of grain sizes from thin sections using stereological methods. The latter point includes an estimate of the volume occupied by a particular grain size fraction and a parameter to measure the shape of the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods assume that grains have equant or near-equant (AR < 2.0) shapes, which includes grains produced during static annealing and dynamically recrystallized grains when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For igneous studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* software (Higgins 2000). See the references list section for details.
+
+***Why use apparent grain size measures instead of measures estimated from unfolded 3D grain size distributions in paleopiezometry studies?***
+One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other unidimensional parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and, hence, the accuracy of the estimates depends not only in the introduction of errors during measuring but also on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, [only approximate](http://doi.wiley.com/10.1111/j.1365-2818.1983.tb04255.x). This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. To sum up, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distribution, otherwise use estimates based on the apparent grain size distribution.
+
+***What "average" (mean, median, peak) apparent grain size measure do I use?***
-***Why use apparent grain size measures instead of measures estimated from the unfolded 3D grain size distribution in paleopiezometry studies?***
-One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other 1D parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and hence the accuracy of the estimates depends on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, only approximate. This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. In short, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distributions, otherwise use measures based on the apparent grain size distribution.
+This depends on the features of the grain size distribution. In the case of unimodal distributions the following rule of thumb should be considered:
-***Why the grain size distribution plots produced by the GST script do not use the same units as the classic CSD charts?***
+- use **mean and standard deviation (SD)** when your **distribution is normal-like**
+- use **median and interquartile (or interprecentil) range** when your **distribution is skewed**
+
+If your distribution is multimodal (two or more frequency peaks), you can use for comparative purposes the **location of the frequency peaks** based on the Kernel density estimate. For more details read the [Scope](https://github.com/marcoalopez/GrainSizeTools/blob/master/DOCS/Scope.md) section.
+
+***What is an MSD value? What is it used for?***
+MSD stands for *Multiplicative Standard Deviation* and it is a parameter that allows to define the shape of the grain size distribution using a single value assuming that it follows a lognormal distribution. In plain language, the MSD value gives a measure of the asymmetry (or skewness) of the grain size distribution. For example, an MSD value equal to one corresponds to a normal (Gaussian) distribution and values greater than one with log-normal distributions of different shapes, being the higher the MSD value the greater the asymmetry of the distribution (Figure a). The advantage of this approach is that by using a single parameter we can define the shape of the grain size distribution independently of its scale (Fig. b), which is very convenient for comparing the shape of two or more grain size distributions.
+
+
+
+*Probability density functions of selected lognormal distributions taken from [Lopez-Sanchez and Llana-Fúnez (2016)](http://www.sciencedirect.com/science/article/pii/S0191814116301778). (a) Lognormal distributions with different MSD values (shapes) and the same median (4). (b) Lognormal distributions with the same shape corresponding to an MSD value (1.5) and different medians (note that different medians imply different scales in the horizontal and vertical directions).*
+
+***Why the grain size distribution plots produced by the GST script and the classic CSD charts do not use the same units on the y axis?***
As you may noticed classic CSDs charts (Marsh, 1988) show in the vertical axis the logarithmic variation in population density or log(frequency) in mm-4, while the stereological methods put in the GrainSizeTools (GST) script returns plots with a linear frequency (per unit volume). This is due to the different aims of the CSDs and the plots returned by the GST script. Originally, CSDs were built for deriving two things in magmatic systems: i) nucleation rates and ii) crystal growth rates. In these systems, small grains are more abundant than the large ones and the increase in quantity is typically exponential. The use of the logarithm in the vertical axis helps to obtain a straight line with the slope being the negative inverse of the crystal growth times the time of crystallization. Further, the intercept of the line at grain size equal to zero allows estimating the nuclei population density. In recrystallized rocks, there is no grain size equal to zero and we usually unknown the crystallization time, so the use of the CSDs are not optimal. Furthermore, the use of the logarithm in the vertical axis has two main disadvantages for microstructural studies: (i) it obscures the reading of the volume of a particular grain fraction, a common target in microtectonic studies, and (ii) it prevents the easy identification of the features of grain size distribution, which is relevant for applying the two-step method.
***Why the sum of all frequencies in the histograms is not equal to one?***
@@ -741,20 +810,26 @@ This is because the script normalized the frequencies of the different classes s
***Is it necessary to specify the version of the script used in a publication? How can this be indicated?***
-Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered a posteriori. The way to indicate the version is twofold:
+Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered later. The way to indicate the version is twofold:
+
+- The easy way we advise you to follow is by explicitly indicating the version in your manuscript as follows: "*...we used the GrainSizeTools script version 1.4.4...*" and then use the general citation in the reference list.
+
+- The other way is by adding a termination in the form *.v plus a number* in the general DOI link. This is, instead of using the general reference of the script:
+
+ Lopez-Sanchez, Marco A. (2018): GrainSizeTools script. figshare.
-- In the text by explicitly indicating it as follows: "*...we used the GrainSizeTools script version 1.4.1...*"
+ https://doi.org/10.6084/m9.figshare.1383130
-- In the reference list by adding a termination in the form *.v plus a number* in the general DOI link. For example:
+ You can modify the doi link as follows:
Lopez-Sanchez, Marco A. (2017): GrainSizeTools script. figshare.
https://doi.org/10.6084/m9.figshare.1383130.v15 (Note the termination *.v15*)
- To know what termination to use go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
+ To get the specific doi link, go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
***Does the script work with Python 2.7.x and 3.x versions? Which version do I choose?***
-Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons and they are widely used, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the author using Python 3.
+Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the maintainer using Python 3.
***I get the results but not the plots when using the Spyder IDE***
This issue is produced because the size of the figures returned by the script are too large to show them inside the console using the **inline** mode. To fix this go to the Spyder menu bar and in ```Tools>Preferences>IPython console>Graphics``` find *Graphics backend* and select *Automatic*.
diff --git a/DOCS/sourceDoc_to_pdf.pdf b/DOCS/sourceDoc_to_pdf.pdf
index c6e5e02..ccf4619 100644
Binary files a/DOCS/sourceDoc_to_pdf.pdf and b/DOCS/sourceDoc_to_pdf.pdf differ
 +*Figure 5. The results windows showing all the measures done on the grains by the ImageJ application.*
-
-*Figure 15. ImageJ I/O options window.*
+
+*Figure 6. ImageJ I/O options window.*
@@ -728,12 +781,28 @@ Barraud, J., 2006. The use of watershed segmentation and GIS software for textur
## Frequently Asked Questions
***Who is this script for?***
-This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate features of the actual 3D distribution of grain sizes from the population of apparent grain sizes measured in thin sections. These features include the estimation of the volume occupied by a particular grain size fraction and the parameters that best describe the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods implemented in the script assume that the grains have equant or near-equant (AR < 2.0) shapes, which includes most dynamically recrystallized grains typically found in crustal and mantle shear zones (olivine, quartz, feldspar or calcite) and ice when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* (Higgins 2000). See the references list section for details.
+This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate the actual (3D) distribution of grain sizes from thin sections using stereological methods. The latter point includes an estimate of the volume occupied by a particular grain size fraction and a parameter to measure the shape of the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods assume that grains have equant or near-equant (AR < 2.0) shapes, which includes grains produced during static annealing and dynamically recrystallized grains when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For igneous studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* software (Higgins 2000). See the references list section for details.
+
+***Why use apparent grain size measures instead of measures estimated from unfolded 3D grain size distributions in paleopiezometry studies?***
+One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other unidimensional parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and, hence, the accuracy of the estimates depends not only in the introduction of errors during measuring but also on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, [only approximate](http://doi.wiley.com/10.1111/j.1365-2818.1983.tb04255.x). This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. To sum up, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distribution, otherwise use estimates based on the apparent grain size distribution.
+
+***What "average" (mean, median, peak) apparent grain size measure do I use?***
-***Why use apparent grain size measures instead of measures estimated from the unfolded 3D grain size distribution in paleopiezometry studies?***
-One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other 1D parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and hence the accuracy of the estimates depends on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, only approximate. This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. In short, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distributions, otherwise use measures based on the apparent grain size distribution.
+This depends on the features of the grain size distribution. In the case of unimodal distributions the following rule of thumb should be considered:
-***Why the grain size distribution plots produced by the GST script do not use the same units as the classic CSD charts?***
+- use **mean and standard deviation (SD)** when your **distribution is normal-like**
+- use **median and interquartile (or interprecentil) range** when your **distribution is skewed**
+
+If your distribution is multimodal (two or more frequency peaks), you can use for comparative purposes the **location of the frequency peaks** based on the Kernel density estimate. For more details read the [Scope](https://github.com/marcoalopez/GrainSizeTools/blob/master/DOCS/Scope.md) section.
+
+***What is an MSD value? What is it used for?***
+MSD stands for *Multiplicative Standard Deviation* and it is a parameter that allows to define the shape of the grain size distribution using a single value assuming that it follows a lognormal distribution. In plain language, the MSD value gives a measure of the asymmetry (or skewness) of the grain size distribution. For example, an MSD value equal to one corresponds to a normal (Gaussian) distribution and values greater than one with log-normal distributions of different shapes, being the higher the MSD value the greater the asymmetry of the distribution (Figure a). The advantage of this approach is that by using a single parameter we can define the shape of the grain size distribution independently of its scale (Fig. b), which is very convenient for comparing the shape of two or more grain size distributions.
+
+
+
+*Probability density functions of selected lognormal distributions taken from [Lopez-Sanchez and Llana-Fúnez (2016)](http://www.sciencedirect.com/science/article/pii/S0191814116301778). (a) Lognormal distributions with different MSD values (shapes) and the same median (4). (b) Lognormal distributions with the same shape corresponding to an MSD value (1.5) and different medians (note that different medians imply different scales in the horizontal and vertical directions).*
+
+***Why the grain size distribution plots produced by the GST script and the classic CSD charts do not use the same units on the y axis?***
As you may noticed classic CSDs charts (Marsh, 1988) show in the vertical axis the logarithmic variation in population density or log(frequency) in mm-4, while the stereological methods put in the GrainSizeTools (GST) script returns plots with a linear frequency (per unit volume). This is due to the different aims of the CSDs and the plots returned by the GST script. Originally, CSDs were built for deriving two things in magmatic systems: i) nucleation rates and ii) crystal growth rates. In these systems, small grains are more abundant than the large ones and the increase in quantity is typically exponential. The use of the logarithm in the vertical axis helps to obtain a straight line with the slope being the negative inverse of the crystal growth times the time of crystallization. Further, the intercept of the line at grain size equal to zero allows estimating the nuclei population density. In recrystallized rocks, there is no grain size equal to zero and we usually unknown the crystallization time, so the use of the CSDs are not optimal. Furthermore, the use of the logarithm in the vertical axis has two main disadvantages for microstructural studies: (i) it obscures the reading of the volume of a particular grain fraction, a common target in microtectonic studies, and (ii) it prevents the easy identification of the features of grain size distribution, which is relevant for applying the two-step method.
***Why the sum of all frequencies in the histograms is not equal to one?***
@@ -741,20 +810,26 @@ This is because the script normalized the frequencies of the different classes s
***Is it necessary to specify the version of the script used in a publication? How can this be indicated?***
-Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered a posteriori. The way to indicate the version is twofold:
+Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered later. The way to indicate the version is twofold:
+
+- The easy way we advise you to follow is by explicitly indicating the version in your manuscript as follows: "*...we used the GrainSizeTools script version 1.4.4...*" and then use the general citation in the reference list.
+
+- The other way is by adding a termination in the form *.v plus a number* in the general DOI link. This is, instead of using the general reference of the script:
+
+ Lopez-Sanchez, Marco A. (2018): GrainSizeTools script. figshare.
-- In the text by explicitly indicating it as follows: "*...we used the GrainSizeTools script version 1.4.1...*"
+ https://doi.org/10.6084/m9.figshare.1383130
-- In the reference list by adding a termination in the form *.v plus a number* in the general DOI link. For example:
+ You can modify the doi link as follows:
Lopez-Sanchez, Marco A. (2017): GrainSizeTools script. figshare.
https://doi.org/10.6084/m9.figshare.1383130.v15 (Note the termination *.v15*)
- To know what termination to use go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
+ To get the specific doi link, go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
***Does the script work with Python 2.7.x and 3.x versions? Which version do I choose?***
-Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons and they are widely used, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the author using Python 3.
+Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the maintainer using Python 3.
***I get the results but not the plots when using the Spyder IDE***
This issue is produced because the size of the figures returned by the script are too large to show them inside the console using the **inline** mode. To fix this go to the Spyder menu bar and in ```Tools>Preferences>IPython console>Graphics``` find *Graphics backend* and select *Automatic*.
diff --git a/DOCS/sourceDoc_to_pdf.pdf b/DOCS/sourceDoc_to_pdf.pdf
index c6e5e02..ccf4619 100644
Binary files a/DOCS/sourceDoc_to_pdf.pdf and b/DOCS/sourceDoc_to_pdf.pdf differ
+*Figure 5. The results windows showing all the measures done on the grains by the ImageJ application.*
-
-*Figure 15. ImageJ I/O options window.*
+
+*Figure 6. ImageJ I/O options window.*
@@ -728,12 +781,28 @@ Barraud, J., 2006. The use of watershed segmentation and GIS software for textur
## Frequently Asked Questions
***Who is this script for?***
-This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate features of the actual 3D distribution of grain sizes from the population of apparent grain sizes measured in thin sections. These features include the estimation of the volume occupied by a particular grain size fraction and the parameters that best describe the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods implemented in the script assume that the grains have equant or near-equant (AR < 2.0) shapes, which includes most dynamically recrystallized grains typically found in crustal and mantle shear zones (olivine, quartz, feldspar or calcite) and ice when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* (Higgins 2000). See the references list section for details.
+This script is targeted at anyone who wants to: i) visualize grain size features, ii) obtain a set of apparent grain size measures to estimate the magnitude of differential stress (or rate of mechanical work) in dynamically recrystallized rocks, and iii) estimate the actual (3D) distribution of grain sizes from thin sections using stereological methods. The latter point includes an estimate of the volume occupied by a particular grain size fraction and a parameter to measure the shape of the population of grain sizes (assuming that the distribution of grain sizes follows a lognormal distribution). The stereological methods assume that grains have equant or near-equant (AR < 2.0) shapes, which includes grains produced during static annealing and dynamically recrystallized grains when bulging (BLG) or sub-grain rotation (SGR) are the main recrystallization process. For igneous studies involving tabular grains far from near-equant objects, we recommend other approaches such as those implemented in the *CSDCorrections* software (Higgins 2000). See the references list section for details.
+
+***Why use apparent grain size measures instead of measures estimated from unfolded 3D grain size distributions in paleopiezometry studies?***
+One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other unidimensional parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and, hence, the accuracy of the estimates depends not only in the introduction of errors during measuring but also on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, [only approximate](http://doi.wiley.com/10.1111/j.1365-2818.1983.tb04255.x). This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. To sum up, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distribution, otherwise use estimates based on the apparent grain size distribution.
+
+***What "average" (mean, median, peak) apparent grain size measure do I use?***
-***Why use apparent grain size measures instead of measures estimated from the unfolded 3D grain size distribution in paleopiezometry studies?***
-One may be tempted to use a stereological method to estimate the midpoint of the modal interval or any other 1D parameter based on the actual grain size distribution rather than using the mean, median, or frequency peak of the apparent grain size distribution. We think that there is no advantage in doing this but serious drawbacks. The rationale behind this is that 3D grain size distributions are estimated using a stereological model and hence the accuracy of the estimates depends on the robustness of the model. Unfortunately, stereological methods are built on "weak" geometric assumptions and the results will always be, at best, only approximate. This means that the precision of the estimated 3D size distribution is **much poorer** than the precision of the original distribution of grain profiles since the latter is based on real data. In short, use stereological methods only when you need to estimate the volume occupied by a particular grain size fraction or investigating the shape of the actual grain size distributions, otherwise use measures based on the apparent grain size distribution.
+This depends on the features of the grain size distribution. In the case of unimodal distributions the following rule of thumb should be considered:
-***Why the grain size distribution plots produced by the GST script do not use the same units as the classic CSD charts?***
+- use **mean and standard deviation (SD)** when your **distribution is normal-like**
+- use **median and interquartile (or interprecentil) range** when your **distribution is skewed**
+
+If your distribution is multimodal (two or more frequency peaks), you can use for comparative purposes the **location of the frequency peaks** based on the Kernel density estimate. For more details read the [Scope](https://github.com/marcoalopez/GrainSizeTools/blob/master/DOCS/Scope.md) section.
+
+***What is an MSD value? What is it used for?***
+MSD stands for *Multiplicative Standard Deviation* and it is a parameter that allows to define the shape of the grain size distribution using a single value assuming that it follows a lognormal distribution. In plain language, the MSD value gives a measure of the asymmetry (or skewness) of the grain size distribution. For example, an MSD value equal to one corresponds to a normal (Gaussian) distribution and values greater than one with log-normal distributions of different shapes, being the higher the MSD value the greater the asymmetry of the distribution (Figure a). The advantage of this approach is that by using a single parameter we can define the shape of the grain size distribution independently of its scale (Fig. b), which is very convenient for comparing the shape of two or more grain size distributions.
+
+
+
+*Probability density functions of selected lognormal distributions taken from [Lopez-Sanchez and Llana-Fúnez (2016)](http://www.sciencedirect.com/science/article/pii/S0191814116301778). (a) Lognormal distributions with different MSD values (shapes) and the same median (4). (b) Lognormal distributions with the same shape corresponding to an MSD value (1.5) and different medians (note that different medians imply different scales in the horizontal and vertical directions).*
+
+***Why the grain size distribution plots produced by the GST script and the classic CSD charts do not use the same units on the y axis?***
As you may noticed classic CSDs charts (Marsh, 1988) show in the vertical axis the logarithmic variation in population density or log(frequency) in mm-4, while the stereological methods put in the GrainSizeTools (GST) script returns plots with a linear frequency (per unit volume). This is due to the different aims of the CSDs and the plots returned by the GST script. Originally, CSDs were built for deriving two things in magmatic systems: i) nucleation rates and ii) crystal growth rates. In these systems, small grains are more abundant than the large ones and the increase in quantity is typically exponential. The use of the logarithm in the vertical axis helps to obtain a straight line with the slope being the negative inverse of the crystal growth times the time of crystallization. Further, the intercept of the line at grain size equal to zero allows estimating the nuclei population density. In recrystallized rocks, there is no grain size equal to zero and we usually unknown the crystallization time, so the use of the CSDs are not optimal. Furthermore, the use of the logarithm in the vertical axis has two main disadvantages for microstructural studies: (i) it obscures the reading of the volume of a particular grain fraction, a common target in microtectonic studies, and (ii) it prevents the easy identification of the features of grain size distribution, which is relevant for applying the two-step method.
***Why the sum of all frequencies in the histograms is not equal to one?***
@@ -741,20 +810,26 @@ This is because the script normalized the frequencies of the different classes s
***Is it necessary to specify the version of the script used in a publication? How can this be indicated?***
-Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered a posteriori. The way to indicate the version is twofold:
+Yes, it is always desirable to indicate the version of the script used. The rationale behind this is that codes may contain bugs and versioning allow to track them and correct the results of already published studies in case a bug is discovered later. The way to indicate the version is twofold:
+
+- The easy way we advise you to follow is by explicitly indicating the version in your manuscript as follows: "*...we used the GrainSizeTools script version 1.4.4...*" and then use the general citation in the reference list.
+
+- The other way is by adding a termination in the form *.v plus a number* in the general DOI link. This is, instead of using the general reference of the script:
+
+ Lopez-Sanchez, Marco A. (2018): GrainSizeTools script. figshare.
-- In the text by explicitly indicating it as follows: "*...we used the GrainSizeTools script version 1.4.1...*"
+ https://doi.org/10.6084/m9.figshare.1383130
-- In the reference list by adding a termination in the form *.v plus a number* in the general DOI link. For example:
+ You can modify the doi link as follows:
Lopez-Sanchez, Marco A. (2017): GrainSizeTools script. figshare.
https://doi.org/10.6084/m9.figshare.1383130.v15 (Note the termination *.v15*)
- To know what termination to use go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
+ To get the specific doi link, go to the script repository at https://figshare.com/articles/GrainSizeTools_script/1383130 , find the version you used in your study, and then click on "Cite" to obtain the full citation.
***Does the script work with Python 2.7.x and 3.x versions? Which version do I choose?***
-Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons and they are widely used, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the author using Python 3.
+Despite both Python versions are not fully compatible, *GrainSizeTools script* has been written to run on both. As a rule of thumb, if you do not have previous experience with the Python language go with 3.x versions, which is the present and future of the language. Python 2.7.x versions are still maintained for legacy reasons, but keep in mind that their support [will be discontinued in 2020](https://pythonclock.org/). Also note that since version 1.3, the script is only tested by the maintainer using Python 3.
***I get the results but not the plots when using the Spyder IDE***
This issue is produced because the size of the figures returned by the script are too large to show them inside the console using the **inline** mode. To fix this go to the Spyder menu bar and in ```Tools>Preferences>IPython console>Graphics``` find *Graphics backend* and select *Automatic*.
diff --git a/DOCS/sourceDoc_to_pdf.pdf b/DOCS/sourceDoc_to_pdf.pdf
index c6e5e02..ccf4619 100644
Binary files a/DOCS/sourceDoc_to_pdf.pdf and b/DOCS/sourceDoc_to_pdf.pdf differ