This project emerged from my fascination with the subject of a book I stumbled upon: 'The Algorithmic Beauty of Plants.' The author, Aristid Lindenmayer, a botanist, developed a mathematical theory to describe plant topology, which later evolved into a framework for modeling the development of branching structures in general. The Lindenmayer Systems or L-Systems, as they became known, found applications far beyond the field of biology in diverse fields such as urbanism, computer graphics, and even programming languages.
I was inspired to attempt a simple and straightforward implementation in JavaScript.
Before I knew it, what started as curiosity evolved into something of a passion that led to two exploratory projects.
This project, Arborator and FASS (here) are being developed not only to expand my knowledge in procedural generation but also as personal challenge to try and take my coding skills to a new level.
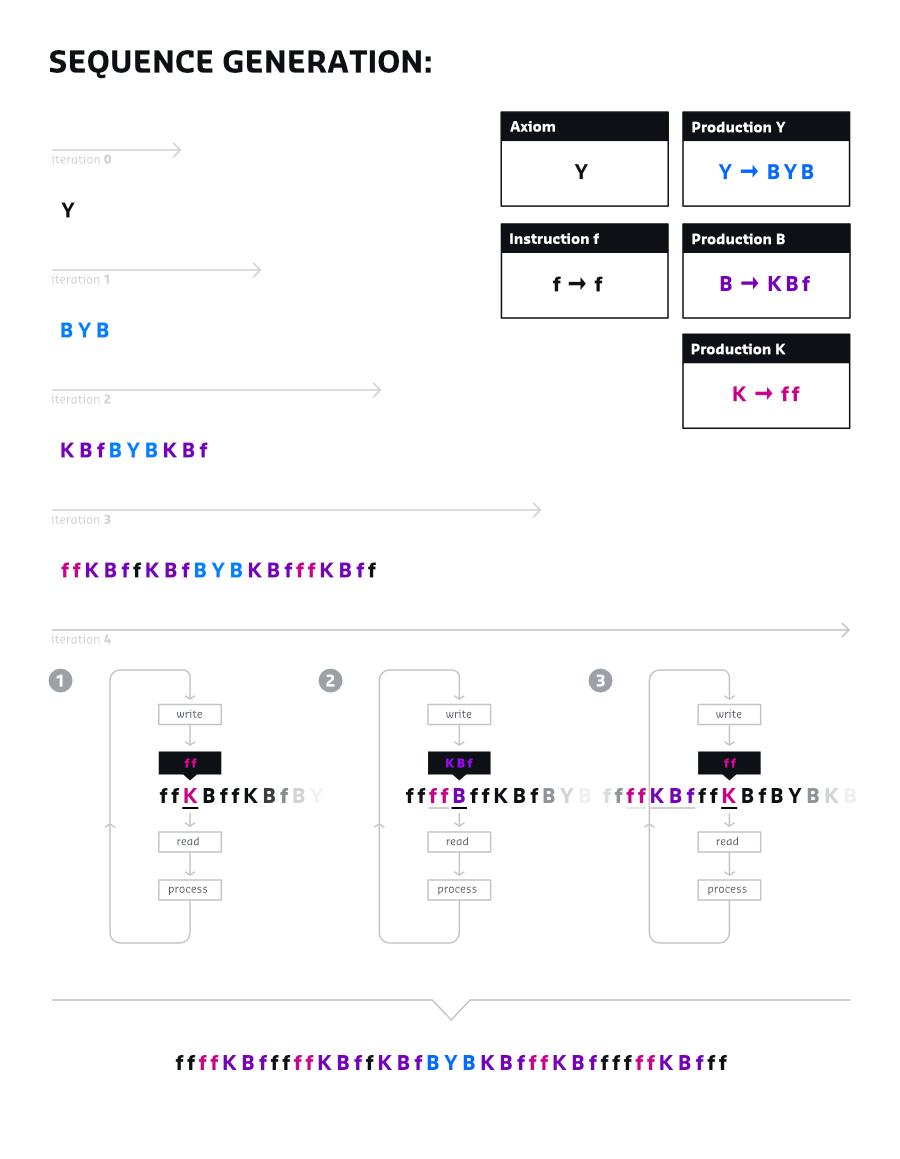
L-Systems are a specialized subset of formal grammars. They are based on a set of symbols, alphabet, that undergo transformations through recursive and iterative processes. Governed by a specific set of production rules, these symbols are systematically replaced in each iteration, resulting in progressively complex strings.
In essence, an L-System consists of:
- An Alphabet: A designated set of symbols.
- Production Rules: The symbol and its respective sequence of symbols that will be added to the sequence.
- An Axiom: The string used to initiate the iterative processes.
Let's consider the simplest model that can be generated using an L-System: the growth of algae.
For this, we need an alphabet with at least 2 symbols, designated as A and B.
Each symbol represents a stage in the organism's growth:
A signifies a directional segment of growth, such as a filament, stem, trunk, or branch.
B represents a branching node.
Next, we define production rules as follows:
A → AB
B → A
These rules instruct us to replace A with AB and B with A.
The axiom serves as our starting point, initially consisting of a single A.
We initiate the process by applying these production rules to every symbol. The first 5 iterations would appear as follows:
AABABAABAABABAABABA
Continuing this iterative process leads to the expansion of the string. With each iteration, new branches (represented by "B") emerge from existing ones, resulting in a natural, self-replicating pattern.
However, 'ABAABABA' remains an abstraction that provides limited insight into the actual configuration and shape of the growing algae. It serves as a topological representation, illustrating how elements are organized in terms of their relative positions but missing spatial relationships such as distance, angle, and length of growth.
While we understand that 'B' represents branching, it only indicates where branching occurs and what follows. We can discern that two 'A's follow, but we remain unaware of their degree of divergence, their directional orientation, or the extent of growth they represent.
This framework aims to provide a set of tools for creators to imagine, reason and write applications using the notation and logic of L-Systems.
The sequences produced by an L-System, in isolation, offer limited information about the visual attributes of the structures they model. As seen in the previous example, we know that 'A' represents a growth segment, and 'B' indicates a branching point. And that’s all. We are left wondering: What are the specifics of the growth, such as its length and direction? Is the unit of growth constant? How does the structure branch out? How do the branches diverge, and at what angle?
ABAABABA
Algorithmic Beauty of Plants addresses covers this problem, and this framework does not depart significantly from what is proposed there. As with all previous graphical interpretations outlined there it also takes a post-processing approach to the problem as well as adopting many of the conventions outlined in the book.
These are the 3 main features/capabilities:
We need symbols such as ‘+’ or ‘-’ for commands that instruct the drawing tool to turn left or right by a defined number of degrees. Other symbols, while less apparent but equally fundamental, include ‘[’ and ‘]’. These brackets encapsulate instructions for saving and restoring the drawing state, enabling the creation of branching structures.
The resulting sequence might now resemble something like this:
A[B][+A][-A[B]][+A[B][-A]][+A[B][-A][+A[B]]]
The new sequence mixes different types of symbols and some degree of discernment logic needs to be implemented for reading the sequence in order to retrieve just what is relevant at this stage for the rewriting and replacement of symbols.
How can we ensure that a descendant production receives and accurately interprets the parameters passed by its progenitor?
Up to this point, we've considered non-parametric L-Systems ie. for each Production Rule and drawing command there’s a single, fixed outcome. Regardless of how intricate the generated sequences, we are ‘stamping’ the same shapes. We are confined to geometric and mechanical structures.
The main problem we face is that the separation between the writing and drawing stages doesn’t allow for Productions to communicate directly. Theoretically, in a L-System each production is processed in parallel and simultaneously, which, in practice, means that a Production won’t have access to the whole and definitive context it needs until the complete sequence is fully rewritten in each iteration step. Furthermore, by the time each rewriting is complete, the connection between a parent Production and its offspring is lost.
That’s what why parameters are needed. When symbols carry additional information, such as numeric values, conditions, or instructions, we not only introduce a higher level of control but also make the system more intuitive to understand and use. Parameters act as influencing factors, akin to sunlight or nutrients, determining the structure and shapes.
Production rules are the fundamental building block for creation in a system like this. Designing with L-Systems involves understanding and mastering their inherent logic. So, how can we provide an experience that allows individuals to freely explore, experiment, and ultimately master not only the system itself but also the rules and commands they define?
The goal here is to identify what is relevant for the creative stage of coding and how to best abstract everything else away so that a whole creation could be defined in a single place.
The solutions to the 3 problems/concerns outlined before also corresponds to 3 components:
Glyphs offer an alternative to a lookup table.
As lightweight wrapper objects, they carry their own type information and bind specific characters to production rules, commands, or instructions, for quick and adequate symbol identification.
By allowing only a single instance for each symbol and binding each symbol to a single function, they safeguard the system against overwriting and functional overlaps.
As objects their primary utility lies in the syntactic classifications they embody.
Which, at the current time consists of:
| Type | Description | Examples |
|---|---|---|
| Rule | Represents a production rule | Y B |
| Instruction | Represents a drawing command or rendering operation | f |
| Marker | Serve as flow controllers and scope annotators during parsing, e.g., delimiter signs | ( ) |
Glyphs also act as exchange tokens between components. They are the system’s currency in the sense that one component can exchange with another to obtain required data or objects. For example, a component needing a Production Rule object may pass a stream of Glyphs to an interfacing component and receive corresponding Production Rules in return, all without having to decode each Glyph to explicitly request the Production Rules. In this manner, Glyphs facilitate the seamless flow of symbols throughout the system.
Think of them as specialized "message bottles" in the long stream of symbols left from one production to another. Prims are like telegraphic pieces of metadata containing information about the type and intended purpose of a parameter. They answer: "What are you, and what should I do with you?"
Similarly as it is done with Glyphs, Prims carry this information. Each Prim comes with a prefix that signifies its role, making them easily distinguishable and actionable.
However, there's more to Prims.
They depend on a pair of Marker Glyphs represented by the parentheses characters. Anything enclosed within these markers is treated as a candidate for parameter data. These parentheses serve a dual purpose:
- They act as enclosures, isolating the Prims from the rest of the sequence. This makes it simple to identify, extract, or even skip over parameter data when scanning the sequence.
- They delegate the task of parsing and interpreting Prims to the very components that need them—Productions and Sprites. By doing this, the system allows each component to decode the Prims according to its logic and requirements.
Introducing a specialized subset of symbols such as these allows for better flow control, making the system not just hierarchical but also modular. It allows, for example, for the framework to be applied in both the contexts of parametric and non-parametric L-Systems alike.
Sprites function almost like middleware in a web framework. The Sequencer-Production operates as a request and response mechanism, and it's here that Sprites play an important role.
Sprites are modular components designed to execute specific logic on Productions. They encapsulate a range of generic behaviors for manipulating Glyph sequences and processing Prims. These modules enable users to incorporate multiple functionalities into a single Production by mixing and matching.
Instead of creating a multitude of specialized Production classes, Sprites allow for one unified Production class to be highly configurable by allowing them to be chained or composed in various orders through which the sequence runs like a stream.
While this framework already includes a few other components and is generating the first results, it is still in its early stages of development. Many design and architectural decisions have yet to endure serious scrutiny and testing. However, the three components I've chosen to document here are foundational to the entire idea and unlikely to change much, at least not in terms of their conceptual definitions. I would dare to say.