| comments | edit_url |
|---|---|
true |
给定非负整数数组 heights ,数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
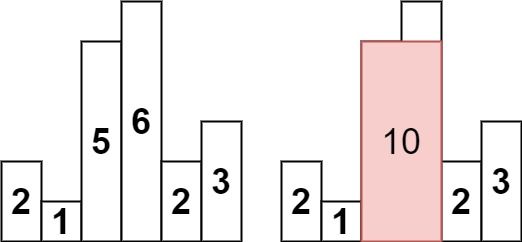
输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
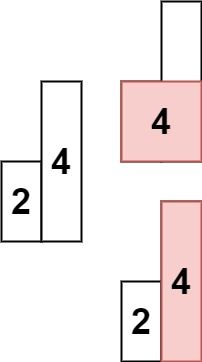
输入: heights = [2,4] 输出: 4
提示:
1 <= heights.length <=1050 <= heights[i] <= 104
注意:本题与主站 84 题相同: https://leetcode.cn/problems/largest-rectangle-in-histogram/
单调栈常见模型:找出每个数左/右边离它最近的且比它大/小的数。模板:
stk = []
for i in range(n):
while stk and check(stk[-1], i):
stk.pop()
stk.append(i)枚举每根柱子的高度
时间复杂度
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
n = len(heights)
left = [-1] * n
right = [n] * n
stk = []
for i, x in enumerate(heights):
while stk and heights[stk[-1]] >= x:
stk.pop()
if stk:
left[i] = stk[-1]
stk.append(i)
stk = []
for i in range(n - 1, -1, -1):
while stk and heights[stk[-1]] >= heights[i]:
stk.pop()
if stk:
right[i] = stk[-1]
stk.append(i)
return max(x * (r - l - 1) for x, l, r in zip(heights, left, right))class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int[] left = new int[n];
int[] right = new int[n];
for (int i = 0; i < n; ++i) {
left[i] = -1;
right[i] = n;
}
Deque<Integer> stk = new ArrayDeque<>();
for (int i = 0; i < n; ++i) {
while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) {
stk.pop();
}
if (!stk.isEmpty()) {
left[i] = stk.peek();
}
stk.push(i);
}
stk.clear();
for (int i = n - 1; i >= 0; --i) {
while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) {
stk.pop();
}
if (!stk.isEmpty()) {
right[i] = stk.peek();
}
stk.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
}class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
vector<int> left(n, -1), right(n, n);
stack<int> stk;
for (int i = 0; i < n; ++i) {
while (!stk.empty() && heights[stk.top()] >= heights[i]) {
stk.pop();
}
if (!stk.empty()) {
left[i] = stk.top();
}
stk.push(i);
}
stk = stack<int>();
for (int i = n - 1; ~i; --i) {
while (!stk.empty() && heights[stk.top()] >= heights[i]) {
stk.pop();
}
if (!stk.empty()) {
right[i] = stk.top();
}
stk.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
};func largestRectangleArea(heights []int) (ans int) {
n := len(heights)
left := make([]int, n)
right := make([]int, n)
for i := range left {
left[i] = -1
right[i] = n
}
stk := []int{}
for i, x := range heights {
for len(stk) > 0 && heights[stk[len(stk)-1]] >= x {
stk = stk[:len(stk)-1]
}
if len(stk) > 0 {
left[i] = stk[len(stk)-1]
}
stk = append(stk, i)
}
stk = []int{}
for i := n - 1; i >= 0; i-- {
for len(stk) > 0 && heights[stk[len(stk)-1]] >= heights[i] {
stk = stk[:len(stk)-1]
}
if len(stk) > 0 {
right[i] = stk[len(stk)-1]
}
stk = append(stk, i)
}
for i, x := range heights {
ans = max(ans, (right[i]-left[i]-1)*x)
}
return
}function largestRectangleArea(heights: number[]): number {
const n = heights.length;
const left: number[] = new Array(n).fill(-1);
const right: number[] = new Array(n).fill(n);
const stk: number[] = [];
for (let i = 0; i < n; ++i) {
while (stk.length && heights[stk[stk.length - 1]] >= heights[i]) {
stk.pop();
}
if (stk.length) {
left[i] = stk[stk.length - 1];
}
stk.push(i);
}
stk.length = 0;
for (let i = n - 1; i >= 0; --i) {
while (stk.length && heights[stk[stk.length - 1]] >= heights[i]) {
stk.pop();
}
if (stk.length) {
right[i] = stk[stk.length - 1];
}
stk.push(i);
}
let ans = 0;
for (let i = 0; i < n; ++i) {
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}class Solution {
func largestRectangleArea(_ heights: [Int]) -> Int {
let n = heights.count
var left = [Int](repeating: -1, count: n)
var right = [Int](repeating: n, count: n)
var stack = [Int]()
for i in 0..<n {
while !stack.isEmpty && heights[stack.last!] >= heights[i] {
stack.removeLast()
}
if !stack.isEmpty {
left[i] = stack.last!
}
stack.append(i)
}
stack.removeAll()
for i in stride(from: n - 1, through: 0, by: -1) {
while !stack.isEmpty && heights[stack.last!] >= heights[i] {
stack.removeLast()
}
if !stack.isEmpty {
right[i] = stack.last!
}
stack.append(i)
}
var maxArea = 0
for i in 0..<n {
maxArea = max(maxArea, (right[i] - left[i] - 1) * heights[i])
}
return maxArea
}
}